Как через расстояние найти объем

Как через расстояние найти объем

Метод объемов в задачах по стереометрии

Метод объемов применяется, когда мы хотим найти расстояние от точки до плоскости.

Или расстояние между двумя скрещивающимися прямыми. Или расстояние между двумя параллельными плоскостями.

Метод объемов состоит в том, чтобы, записав двумя разными способами объем какой-либо треугольной пирамиды и приравняв эти выражения, найти нужную нам величину.

Вот как он применяется в задачах ЕГЭ:

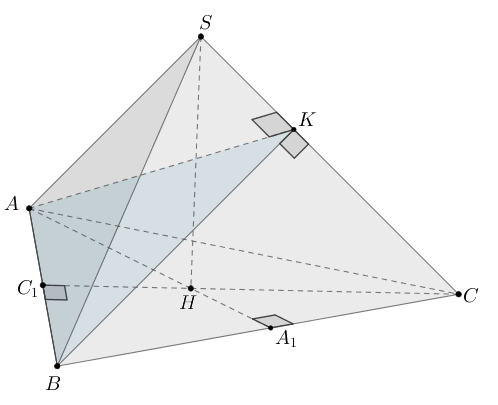
9. В правильной треугольной призме ABCA_{1}B_{1}C_{1} сторона AB основания равна 12, а высота призмы равна 2. На рёбрах B_{1}C_{1} и AB отмечены точки P и Q соответственно, причём PC_{1}=3, а AQ=4. Плоскость A_{1}PQ пересекает ребро BC в точке M.

а) Докажите, что точка M является серединой ребра BC.

б) Найдите расстояние от точки B до плоскости A_{1}PQ.

Построим сечение призмы плоскостью A_1PQ.

Проведём QM parallel {A}_1P в плоскости ABC, точка M лежит на ребре BC.

Мы пользуемся здесь тем, что линии пересечения параллельных плоскостей третьей плоскостью параллельны. Трапеция QMPA_{1} — искомое сечение.

а) Покажем, что M — середина BC.

Пусть P_1 — проекция точки P на плоскость ABC,P_1C=3.Тогда AP_1 parallel A_1P

Пусть BM = x, triangle QBMsim triangle { }A{BP}_1 (по двум углам)

frac{BQ}{AB}=frac{BM}{{BP}_1};

frac{8}{12}=frac{x}{9}

Отсюда x = 6 и M — середина BC.

б) Найдем расстояние от точки B до плоскости A_1PQ, пользуясь методом объемов.

Выразим двумя способами объем треугольной пирамиды A_1QMB. V_{A_1QMB}=frac{1}{3}S_{triangle { QMB}}cdot h_1=frac{1}{3}S_{triangle { }A_1{ QM}}cdot h_2{, } где h_1 — расстояние от точки A_{1} до плоскости QMB, то есть до плоскости основания призмы.

Оно равно высоте призмы, то есть h_1=2.

h_2 — искомое расстояние от точки B до плоскости A_1{ QM.}

S_{triangle { QMB}}=frac{1}{2}cdot BQcdot BMcdot sin60^circ =frac{1}{2}cdot 8cdot 6cdot frac{sqrt{3}}{2}=12sqrt{3;}

Из triangle { }QMB по теореме косинусов:

{QM}^2={BQ}^2+{BM}^2-2BQcdot BMcdot cos60^circ,

{QM}^2=64+36-2cdot 8cdot 6cdot frac{1}{2}=100-38=52;

QM=sqrt{52}=2sqrt{13};

Из triangle { }AA_1Q:

A_1Q=sqrt{{AQ}^2+{AA_1}^2}=sqrt{16+4}=2sqrt{5}.

Точка M — середина BC, AM=frac{12sqrt{3}}{2}=6sqrt{3}.

Из прямоугольного треугольника{{ A}}_{{ 1}}AM найдем A_1M = 4sqrt{7}.

Рассмотрим треугольник A_1QM, в котором мы знаем все стороны.

По теореме косинусов:

A_1Q^2=A_1M^2+QM^2-2QMcdot A_1Mcdot cosangle A_1MQ,

20= 112+52 - 2cdot 8cdot sqrt{7}cdot sqrt{13}cdot cosangle A_1MQ;

cosangle A_1MQ=frac{9}{sqrt{91}}

Тогда sinangle A_1MQ=sqrt{frac{10}{91}}

S_{triangle { }A_1QM}=frac{1}{2}QMcdot A_1Mcdot sinangle A_1MQ=

=frac{1}{2}cdot 2sqrt{13}cdot 4sqrt{7}cdot sqrt{frac{10}{91}}=4sqrt{10};

Объем пирамиды A_1QBMV_{{ }A_1QBM}=frac{1}{3}S_{triangle { }QBM}cdot AA_1=frac{1}{3}S_{{ }A_1QM}cdot h_2,

Отсюда

h_2=frac{S_{triangle { }QBM}cdot { A}A_1}{S_{{ }A_1QM}}=frac{12sqrt{3}cdot 2}{4sqrt{10}}=frac{3sqrt{30}}{5}.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Метод объемов в задачах по стереометрии» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Из нескольких равноудалённых друг от друга точек, образована фугура. Известно, что расстояние между двумя такими точками равно 10 метрам. Чему равен её объём?

Если известно несколько таких фигур, то достаточно сделать соответствующие расчёты для любых двух из них.

Вроде бы подходит только лишь полностью тетраэдр под условия вашей задачи.У него 4 вершины,расстояния между любыми двумя вершинами одинаковое.Если взять куб,например,то в нём диагональные расстояния отличаются от длин рёбер,а я понял условие задачи так что все расстояния между любыми данными точками одинаковое.Найдем объём тетраэдра длиной ребра 10 метров.V=a^3*корень из двух/12=1000*1,44/12­=1200 куб.м(приблизительно­)

автор вопроса выбрал этот ответ лучшим

Знаете ответ?

Источник

ВАЖНО!

Многогранники. Объемы многогранников. Метод объемов.

Методом объёмов называется приравнивание двух подходящих выражений для объёма, в результате чего удаётся вычислить искомую величину (расстояние или угол).

Чтобы воспользоваться методом объемов, нужно найти подходящую треугольную пирамиду и провести вычисления.

Метод объёмов можно использовать, вычисляя:

  • Расстояние от точки М до плоскости α

ρ(M;α) = ρ(M; ABC) =$frac{3V_{ABCM}}{S_{ABC}}$

$V_{ABCM}$ -объем пирамиды АВСМ,

ρ(M;α) – расстояние от точки M до плоскости $alpha$,

$S_{АВС}$- площадь треугольника АВС

  • Угол между плоскостями

$ V = frac{2}{3}cdot frac{S1cdot S2}{a}cdot sin ϕ $

Здесь S1 и S2 — площади двух граней пирамиды, a— общее ребро этих граней, ϕ — угол между плоскостями этих граней.

  • Расстояние между скрещивающимися прямыми

$V = frac{1}{6}acdot bcdot dcdot sin ϕ$

Здесь a и b — скрещивающиеся рёбра тетраэдра, d и ϕ — соответственно расстояние и угол между ними (точнее, между прямыми, содержащими эти рёбра).

Источник

Описание презентации по отдельным слайдам:

  • Метод объемов в задачах по стереометрии Учитель математики...

    1 слайд

    Метод объемов в задачах по

    стереометрии

    Учитель математики
    высшей квалификационной категории
    Максимова Марина Олеговна

  • Метод объемов применяется, когда необходимо найти: расстояние от точки до пл...

    2 слайд

    Метод объемов применяется, когда необходимо найти:

    расстояние от точки до плоскости;

    расстояние между двумя скрещивающимися прямыми;

    расстояние между двумя параллельными плоскостями.

    Метод объемов состоит в том, чтобы, записав двумя разными способами объем

    какой-либо треугольной пирамиды и приравняв эти выражения, найти искомую

    величину.

  • ЗАДАЧА В правильной треугольной призме ABCA1B1C1 сторона AB основания ра...

    3 слайд

    ЗАДАЧА
    В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а высота призмы равна 2. На рёбрах В1C1 и AB отмечены точки P и Q соответственно, причём PC1=3 , а AQ=4. Плоскость   пересекает ребро BC в точке M.

    а) Докажите, что точка M является серединой ребра BC.

    б) Найдите расстояние от точки B до плоскости 

  • Докажем, что М- середина ВС. Пусть P1 – проекция точки P на плоскость АВС,...

    4 слайд

    Докажем, что М- середина ВС.

    Пусть P1 – проекция точки P на плоскость АВС, Р1С=3.
    Тогда АР1  А1Р.

    Пусть ВМ = х, QBM~ ABP1 ( по двум углам)

    𝐵𝑄 𝐴𝐵 = 𝐵𝑀 𝐵𝑃1 ;

    8 12 = 𝑥 9 ;

    𝑥 = 6 и М – середина ВС.

  • б) Найдем расстояние от точки В до плоскости А1РQ, пользуясь методом объемов....

    5 слайд

    б) Найдем расстояние от точки В до плоскости А1РQ, пользуясь методом объемов.

    Выразим двумя способами объем треугольной пирамиды A1QMB.

    V A1QMB = 1 3 S QBM · h1 = 1 3 S A1QM · h2 ,

    где h1 – расстояние от точки A1 до плоскости QMB, то есть до плоскости основания призмы.

    Оно равно высоте призмы, то есть h1 = 2.

    h2 – искомое расстояние от точки В до плоскости A1QM.

  • Из QBM по теореме косинусов: QM2 = BQ2 + BM2 - 2BQ ·BM · cos 60 , Q...

    6 слайд

    Из QBM по теореме косинусов:

    QM2 = BQ2 + BM2 – 2BQ ·BM · cos 60 ,

    QM2 = 64+36 – 2 ·8 ·6 · 1 2 = 100 – 38 = 52 ;

    QM = 52 = 2 13 ;

    Из АА1Q :

    A1Q = AQ2 + AA1 2 = 16 + 4 = 2 5 .

    Точка M – середина ВС, АМ = 12 3 2 = 6 3 .

    Из прямоугольного А1AM найдем А1М = 4 7 .

  • Рассмотрим А1QM, в котором известны все стороны. Q A1M2 5 4 7 2 13

    7 слайд

    Рассмотрим А1QM, в котором известны все стороны.

    Q

    A1
    M
    2 5
    4 7
    2 13

  • По теореме косинусов: A1Q2 = A1M2 + QM2 - 2QM ·A1M · cos 𝐴1𝑀𝑄 , 20=...

    8 слайд

    По теореме косинусов:

    A1Q2 = A1M2 + QM2 – 2QM ·A1M · cos 𝐴1𝑀𝑄 ,

    20= 112 + 52 – 2 · 8 · 7 · 13 · cos 𝐴1𝑀𝑄 ,

    cos 𝐴1𝑀𝑄 = 9 91 .

    Тогда sin 𝐴1𝑀𝑄 = 10 91

    S A1QM = 1 2 ·QM ·A1M · sin 𝐴1𝑀𝑄 = 1 2 ·2 13 ·4 7 · 10 91 = 4 10

    V A1QMB = 1 3 S QBM · h1 = 1 3 S A1QM · h2,

    Отсюда h2 = S QBM · AA1 S A1QM = 2·12 3 4 10 = 3 30 5

Источник

Тема 13.

Задачи по стереометрии

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами – ЛЕГКО!

Подтемы раздела

задачи по стереометрии

Решаем задачи

Показать ответ и решение

а) Из условия следует, что VBAMN = 1⋅4⋅5 = 20. 3 3 Объемы тетраэдров, имеющих
общий трехгранный угол, относятся как произведения ребер, образующих этот
трехгранный угол. Следовательно,

230 VBAMN- BA-⋅BM--⋅BN- -BN- BN-- 1 BN-- 1 40 = VABCD = BA ⋅BC ⋅BD = 2BD ⇒ BD = 3 ⇒ ND = 2.

Чтд.

PIC

б) По условию BD — высота тетраэдра ABCD. Следовательно,

1 40 =VABCD = 3 ⋅BD ⋅SABC ⇒ SABC = 8.

Так как медиана треугольника делит его на два равновеликих треугольника,
то SAMB = 12SABC = 4. △AMB — проекция △AMN на плоскость
ABC. Следовательно, косинус угла между плоскостями AMN и ABC
равен

SAMB- 4 4 cosα = SAMN = 5 ⇒ α= arccos5 .

Ответ:

б) arccos 4 5

В правильной треугольной пирамиде SABC проведено сечение плоскостью,
проходящей через сторону основания AB перпендикулярно ребру SC.

а) Докажите, что площадь сечения относится к площади основания пирамиды
так же, как высота пирамиды относится к ее боковому ребру.

б) Найдите площадь сечения пирамиды, если боковое ребро SA = 5, а сторона
основания AB = 4.

Показать ответ и решение

а) Пусть ABK — сечение пирамиды SABC плоскостью, перпендикулярной SC
и проходящей через AB. Так как SC ⊥ (ABK ), то SK — высота пирамиды
SABK.

Объемы тетраэдров, имеющих общий трехгранный угол, относятся как
произведения ребер, образующих этот трехгранный угол. Следовательно,

VSABK-= SA-⋅SB-⋅SK-= SK-. VSABC SA ⋅SB ⋅SC SC

С другой стороны,

VSABK- 13SK-⋅SABK- VSABC = 13SH ⋅SABC .

Отсюда

1 SK-= -31SK-⋅SABK ⇒ SH-= SABK-. SC 3SH ⋅SABC SC SABC

Чтд.

PIC

б) Из пункта а) следует, что

SH ⋅S SH ⋅ AB2√3 SABK = ---SCABC-= ----SC-4--.

Высота правильного треугольника со стороной a равна √ - a23 , следовательно,
CC1 = 2√3, а CH = 2CC1 = √4-. 3 3 Тогда по теореме Пифагора ∘ -- SH = 59. 3
Следовательно,

∘-59-⋅ 42√3 SABK = --3---4--= 4√59. 5 5

Ответ:

б) √-- 4-59- 5

В правильной шестиугольной призме ABCDEF A1B1C1D1E1F1 все ребра равны
1.

а) Докажите, что точки F и C равноудалены от плоскости BED1.

б) Найдите расстояние между прямыми ED1 и FE1.

Показать ответ и решение

а) Так как плоскость пересекает две параллельные плоскости по параллельным
прямым, то плоскость A1B1C1 плоскость BED1 пересечет по прямой
C1D1 ∥BE. Пусть FC ∩ BE = O. Тогда O — центр правильного
шестиугольника, следовательно, FO = CO = AB = 1. Пусть FHF и CHC —
перпендикуляры из точек F и C на плоскость BED1 соответственно. Тогда
△F OHF = △COHC как прямоугольные по гипотенузе и острому углу
(∠F OH = ∠COH F C как вертикальные). Следовательно, FH = CH . F C
Чтд.

PIC

В задаче 41859 была доказана формула

V = 1abdsin α, 6

где a,b — противоположные ребра тетраэдра, d — расстояние между ними,
α — угол между ними. Будем пользоваться этой формулой, чтобы найти
расстояние между ребрами ED1 и FE1 тетраэдра FED1E1.

В наших обозначениях объем этого тетраэдра равен

V = 1 ⋅ED1 ⋅F E1⋅d⋅sin α, 6

где α — угол между ED1 и FE1.

Заметим, что отрезки ED1 и FE1 равны √2. Так как FO = E1D1 и
F O ∥ E1D1, то FE1D1O — параллелограмм, следовательно, OD1 ∥F E1,
следовательно, ∠OD1E =α — угол между ED1 и F E1. Найдем его по теореме
косинусов из △OD1E, где √ - OD1 = ED1 = 2, OE = 1:

√ - cosα= 2+√2−√1-= 3 ⇒ sinα = --7. 2⋅ 2⋅ 2 4 4

С другой стороны, объем тетраэдра FED E 1 1 равен

2 SEFE1 ⋅SED1E1 ∘ V = 3 ⋅ EE1 ⋅sin120

по формуле, которая доказывалась в задаче 41979 ( ∘ ∠F ED = 120 и есть угол
между гранями EF E1 и ED1E1 ).

Заметим, что SEFE1 = SED1E1 = 12. Следовательно,

√-- 1 ⋅ED1 ⋅F E1⋅d⋅sin α= 2 ⋅ SEFE1-⋅SED1E1-⋅sin120∘ ⇒ d= -21. 6 3 EE1 7

Ответ:

б) √-- -21- 7

Показать ответ и решение

Так как (CC1D1 )∥(AA1B1), то можно искать угол между плоскостью D1MK и
плоскостью AA1B1. Назовем этот угол α.

В задаче 41979 была доказана формула

2SP V = 3-a-sinα.

для объема треугольной пирамиды, где S и P — площади двух граней, a —
их общее ребро, α — угол между плоскостями этих граней.

Если рассмотреть тетраэдр D1A1MK, то его объем равен

2 SA1MK-⋅SD1MK- V = 3 ⋅ MK ⋅sinα.

С другой стороны, его объем равен

1 V = 3D1A1 ⋅SA1MK.

Отсюда

D1A1-⋅MK-- sin α= 2SD1MK .

PIC

Следовательно,

4⋅5 √2- sinα = ----√--= -2- ⇒ α =45∘. 2⋅10 2

Ответ:

45∘

Показать ответ и решение

Ответ:

1 2

Показать ответ и решение

В задаче 41979 была доказана формула

V = 2 pqsinα. 3 x

для объема треугольной пирамиды, где p и q — площади двух граней, x —
их общее ребро, α — угол между плоскостями этих граней. Если обозначить
AB = x, SABD =p, SABC = q, то по этой формуле объем тетраэдра ABCD
равен

V = 2 ⋅ pq⋅sin α. 3 x

Заметим, что центр шара, вписанного в тетраэдр, лежит на пересечении
биссекторных плоскостей тетраэдра. Следовательно, плоскость AOB — биссектор,
то есть делит двугранный угол, образованный гранями ABD и ABC,
пополам.

PIC

В задаче 46419 в ходе решения была доказана формула

VD- p --q- VC = q ⇒ VC = p+ qV,

где VD = VDAOB, VC = VCAOB.

Проведем CH ⊥ (AOB ). Пусть CX ⊥ AB, тогда по теореме о трех
перпендикулярах HX ⊥AB. Следовательно, ∠CXH = α. 2 Пусть CX = c,
OK = h — высота △AOB, проведенная к AB = x. Тогда CH = csin α 2
и

1 α 1 VC = 3 ⋅csin 2-⋅2 ⋅hx.

Тогда из VC = pq+qV получаем равенство

1 α 1 q 2 pq 1 2pq α 3 ⋅csin 2-⋅2 ⋅hx = p+-q ⋅3 ⋅x-⋅sin α ⇔ SAOB = 2hx = p+-q cos2.

(так как cx =2q )

Ответ:

-2pq cos α p + q 2

Показать ответ и решение

Ответ:

2 a 3

Показать ответ и решение

Пусть A1H и O1P — перпендикуляры на плоскость BC1D. Тогда
△A1HC1 ∼ △O1P C1 с коэффициентом подобия k =2 = A1C1 :O1C1.
Следовательно, 1 O1P = 2A1H. Будем искать A1H.

Рассмотрим тетраэдр A1BC1D. Его объем равен 13 от объема параллелепипеда.
Действительно,

1 1 1 Vт = Vп−(VA1ABD +VC1CBD )− (VBA1B1C1 + VDA1D1C1)= Vп−3Vп− 3Vп = 3 Vп.

PIC

С другой стороны, если обозначить за h расстояние от точки A1 до плоскости
BC1D, объем этого тетраэдра равен

1 Vт = 3 ⋅h⋅SBC1D.

Следовательно,

--Vп-- h = SBC1D.

Следовательно,

O1P = 1h = 1⋅ -Vп---= 2a. 2 2 SBC1D 3

Ответ:

2 a 3

Докажите, что биссектор двугранного угла при ребре тетраэдра делит
противоположное ребро на части, пропорциональные площадям граней тетраэдра,
лежащих на гранях этого угла.

Показать ответ и решение

Так как AB1 ∥ DC1, то расстояние между прямыми AD1 и DC1 равно
расстоянию от любой точки прямой DC1 до плоскости AB1D1. Пусть h —
расстояние от C1 до этой плоскости. Рассмотрим тетраэдр AB1C1D1 . Запишем
его объем двумя способами:

1 1 AA1⋅SB1C1D1- 3 ⋅AA1 ⋅SB1C1D1 = V = 3 ⋅h ⋅SAB1D1 ⇒ h= SAB1D1 .

PIC

  • AB = actg α, BC = actgβ ⇒

    3 Vп = a ctgαctgβ.

  • Пусть ∠B1AD1 =φ.

    AD1 = BC1 = -a-, sinβ AB1 = -a-, sinα
    ∘ ----------- ∘ --------------- B1D1 =a ctg2α +ctg2β = a --12--+ --12--− 2. sin α sin β

    Следовательно,

    2 2 2 cosφ = AD-1 +-AB-1 −-B1D1 = sinα sinβ. 2⋅AD1 ⋅AB1

    Тогда ∘ -----2----2-- sinφ= 1− sin α sin β. Следовательно,

    ∘ ------------- SAB D = 1 ⋅AD1 ⋅AB1 ⋅sin φ= a2--1−-sin2α-sin2β. 1 1 2 2sinα sinβ

  • SB1C1D1 = 1a2ctg αctgβ. 2

Тогда

a⋅ 1a2ctgαctgβ acosαcosβ h = a22√1−sin2αsin2β-= ∘1-−-sin2αsin2β-. ---2sinαsinβ---

Ответ:

∘--acosαcosβ--- 1 − sin2 αsin2β

Показать ответ и решение

Рассмотрим тетраэдр A1BC1D. Его объем равен 1 3 от объема параллелепипеда.
Действительно,

Vт = Vп−(VA ABD +VC CBD )− (VBA B C + VDA D C )= Vп− 1Vп− 1Vп = 1 Vп. 1 1 1 1 1 1 1 1 3 3 3

PIC

С другой стороны, если обозначить за h расстояние от точки A1 до плоскости
BC1D, объем этого тетраэдра равен

Vт = 1 ⋅h⋅SBC1D. 3

Следовательно,

Vп h = SBC1D.

  • AB = actg α, BC = actgβ ⇒

    Vп = a3ctgαctgβ.

  • Пусть ∠BC1D = φ.

    -a-- BC1 = sinβ, -a-- DC1 = sinα,
    ∘ --------------- BD = a∘ctg2α+-ctg2β-= a --1--+ --1--− 2. sin2α sin2β

    Следовательно,

    BC21 +-DC21 −-BD2 cosφ= 2⋅BC1 ⋅DC1 = sinαsin β.

    Тогда ------------- sinφ= ∘ 1− sin2α sin2β. Следовательно,

    2∘------2---2-- SBC1D = 1⋅BC1 ⋅DC1 ⋅sinφ = a--1-−-sin-αsin-β-. 2 2 sinα sinβ

Тогда

2acosα cosβ h = ∘1-−-sin2αsin2β-.

Ответ:

∘-2a-cosα-cosβ--- 1 − sin2 αsin2β

Показать ответ и решение

Проведем CD1 ∥BA1. Тогда BA1 ∥ (B1CD1 ), следовательно, расстояние между
прямыми BA1 и CB1 равно расстоянию между прямой BA1 и плоскостью
B1CD1, а оно в свою очередь равно расстоянию от любой точки прямой BA1 до
этой плоскости.

Пусть h — расстояние от точки A1 до плоскости B1CD1. Рассмотрим
тетраэдр CA1B1D1. Запишем его объем:

1⋅CC1 ⋅SA1B1D1 = V = 1 ⋅h ⋅SB1CD1 ⇒ h= CC1⋅SA1B1D1. 3 3 SB1CD1

PIC

  • S = 1⋅3 ⋅3 = 9. A1B1D1 2 2

  • △B1CD1 — равносторонний, его стороны равны диагоналям квадратов
    со стороной 3. Так как B1D1 = 3√2, то

    √ - √ - SB CD = B1D21--3= 9--3. 1 1 4 2

Следовательно,

3⋅ 9 √ - h = 9√23-= 3. 2

Ответ:

√3-

В правильной треугольной пирамиде отношение бокового ребра к высоте пирамиды
равно 2. Найдите отношение радиуса вписанного в пирамиду шара к стороне
основания пирамиды.

Показать ответ и решение

Пусть боковое ребро пирмиды равно 2x, высота пирамиды SH = x, сторона
основания равна a, а радиус вписанного в пирамиду шара равен r. Запишем
объем пирамиды SABC двумя разными способами:

1 1 -SH--⋅SABC--- 3 ⋅SH ⋅SABC =V = 3 (SABC + 3SSBC)⋅r ⇔ r = SABC +3SSBC .

Пусть AA1 ⊥ BC. Тогда по теореме Пифагора √- AH = 3x, следовательно,
- AA1 = 32AH = 3√23 x. Так как высота правильного треугольника равна - a√32 ,
то

√- √- 3-3- a-3- 2 x= 2 ⇒ a= 3x.

PIC

Следовательно,

a2√3- 9√3 2 SABC = --4--= -4--x.

√- HA1 = 12AH = 23x. Следовательно, по теореме Пифагора √- SA1 = -72 x.
Тогда

√- SSBC = 1⋅SA1 ⋅BC = 3-7-x2 2 4

Следовательно,

√ - ----3-- -r -r ---1--- r = √3 +√ 7x ⇒ a = 3x = 3+ √21.

Ответ:

---1√-- 3 + 21

Показать ответ и решение

Пусть h — расстояние от точки m до плоскости DA1C1. Рассмотрим тетраэдр
C1A1MD. Запишем его объем:

1 ⋅C1B1⋅SA MD = V = 1 ⋅h ⋅SDA C ⇒ h= C1B1⋅SA1MD-. 3 1 3 1 1 SDA1C1

PIC

По теореме Пифагора A1C1 = 2, √- A1D = C1D = 6. Пусть DO ⊥ A1C1. Так
как △DA1C1 равнобедренный, то OC1 = 1. Следовательно, по теореме Пифагора
DO =√5.

Следовательно,

C1B1 ⋅ 1⋅AD ⋅A1M √2-⋅ 1⋅√2-⋅1 1 h= ---1-⋅D2O--⋅A1C1-- = --1-2⋅√5-⋅2--= √5. 2 2

Ответ:

√1- 5

Показать ответ и решение

Так как △ABC равносторонний, то △AMK также равносторонний,
следовательно, ∘ ∠AMK = ∠ABC = 60 как соответственные, значит, MK ∥ BC.
Из условия следует, что

AM 2 AM 2 AB--= 3 ⇒ MB--= 1.

Пусть AA1 — высота основания, тогда если SH — высота пирамиды, то
H ∈ AA1. По обратной теореме Фалеса, так как AM :MB = AH :HA1 = 2:1
имеем MH ∥BC. Следовательно, H ∈ MK.

PIC

Заметим, что так как MK ∥BC, то MK ∥(SBC ), следовательно, то
расстояние от любой точки прямой MK до плоскости SBC будет одинаковым.
Пусть h — расстояние от точки H до плоскости SBC. Запишем объем
пирамиды SHBC двумя разными способами:

1 1 SH-⋅SBHC- 3 ⋅SH ⋅SBHC = V = 3 ⋅h ⋅SBSC ⇒ h = SBSC .

Так как высота правильного треугольника со стороной a равна √- a32 , то
√- AA1 = 3 3 ⇒ √- HA1 = 3. Тогда

1 √- √ - SBHC = 2 ⋅ 3⋅6 = 3 3.

По теореме Пифагора апофема

∘ √------√---- 1 SA1 = ( 6)2+ ( 3)2 = 3 ⇒ SBSC = 2 ⋅3 ⋅6= 9.

Следовательно,

√- √ - h = -6-⋅3--3= √2. 9

Ответ:

√2-

Показать ответ и решение

Пусть M и N — середины BC и CD соответственно. Назовем плоскость
SMN плоскостью α. Так как AB ∥ CD, то угол между AB и α равен углу
между CD и α. Проведем CP ⊥ α. Тогда NP — проекция CN на α.
Следовательно,

φ= ∠(CN, α)= ∠CNP.

Найдем CP. Запишем объем пирамиды SCMN двумя разными способами:

1 ⋅SH ⋅SCMN = V = 1⋅CP ⋅SSMN ⇒ CP = SH-⋅SCMN-, 3 3 SSMN

где SH — высота пирамиды SABCD.

PIC

Вычислим нужные величины.

Следовательно,

CP = -3√⋅4-= √6--. 2 13 13

Тогда

CP 3 3 sin φ= CN- = √26- ⇒ φ= arcsin√26-.

Ответ:

arcsin √3-- 26

Дан куб ABCDA1B1C1D1 с ребром 1, T — середина ребра AD.

а) Докажите, что объем пирамиды AA1T B в 12 раз меньше объема
куба.

б) Найдите расстояние от вершины A до плоскости A1BT.

Показать ответ и решение

а) Объем куба равен Vкуб = 1. Объем пирамиды AA1T B равен

V = 1 ⋅AA1⋅SABT = 1 ⋅AA1⋅ 1⋅AB ⋅AT = 1 ⋅1 ⋅ 1⋅1⋅ 1=-1 = 1-Vкуб 3 3 2 3 2 2 12 12

PIC

б) Запишем объем пирамиды AA1BT двумя разными способами, обозначив за
h искомое расстояние от точки A до плоскости A1BT :

1 1 1 1 12 = 3 ⋅AA1 ⋅SABT = V = 3 ⋅h ⋅SA1BT ⇒ h= S--4--. A1BT

Заметим, что △AA1T = △ABT как прямоугольные по двум катетам.
Следовательно, A1T = BT, значит, △A1BT равнобедренный. Пусть TP — его
высота, проведенная к основанию. По теореме Пифагора ∘ ---1- √5 A1T = 1+ 4 =-2 ,
√ - A1B = 2. Следовательно, √- TP = -32 . Тогда

1 √3 √- 1√- SA1BT = 2 ⋅-2-⋅ 2 = 4 6.

Следовательно,

1 h= -1√4-= 1√-. 4 6 6

Ответ:

б) 1√-- 6

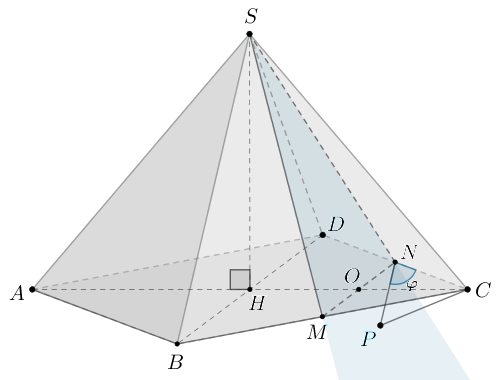
В правильной треугольной пирамиде SABC с основанием ABC боковое ребро
равно 5, а сторона основания равна 6.

а) Докажите, что AS ⊥ BC.

б) Найдите расстояние от вершины A до плоскости SBC.

Показать ответ и решение

а) Пусть AA1 и CC1 — высоты основания пирамиды, которые пересекаются в
точке H. Тогда SH — высота пирамиды. AA1 — проекция наклонной SA на
плоскость ABC. Следовательно, так как AA1 ⊥ BC, по теореме о трех
перпендикулярах SA ⊥ BC.

PIC

б) Объем пирамиды SABC равен

1⋅SH ⋅S = V = 1⋅h ⋅S ⇒ h = SH-⋅SABC, 3 ABC 3 SBC SSBC

где h — искомое расстояние от точки A до плоскости SBC.

Тогда

√- √13 ⋅ 6243 3√ -- h = --1⋅4⋅6--= 4 39. 2

Ответ:

б) √-- 3-39- 4

Показать ответ и решение

Ответ:

б) 120 :19

Источник

Добавить комментарий