Недавно один из читателей прислал мне следующий вопрос:
Здравствуйте! Одним из постулатов, на которых основывается теория относительности является утверждение о том, что скорость света не зависит от системы отсчёта. Но ведь по сути это ни на чем не основанная догадка Эйнштейна. С чего он вообще это взял?
Что же, давайте разберёмся в этом вместе. У многих людей, в особенности у людей, которые физику последний раз учили лет двадцать назад в школе может сложиться впечатление, что Эйнштейн основные постулаты теории относительности взял с потолка.
Постулат о равноправии всех инерциальных систем отсчёта мало у кого вызывает сомнения — все же он довольно интуитивен. А вот постулату об инвариантности скорости света повезло меньше. Судя по тем вопросам, что я получаю многие считают его просто прихотью Эйнштейна.
На самом деле это совсем не так. Предпосылки для появления гипотезы о том, что скорость света не зависит от системы отсчёта появились еще в середине 19-го века лет за 20 до рождения Эйнштейна. Произошло это когда британский физик Джеймс Клерк Максвелл опубликовал свои знаменитые уравнения, описывающие электромагнитное поле.
При решении уравнений Максвелла внезапно оказалось, что скорость света совершенно не зависит от системы отсчёта.
Возникло противоречие c первым законом Ньютона, а также с галилеевым принципом относительности. Ведь до этого считалось, что к примеру если человек стоит на пероне, а мимо едет поезд с постоянной скоростью, то можно в качестве системы отсчёта использовать как человека, и тогда он находится в состоянии покоя, а поезд движется, так и поезд, и тогда в этой системе отсчёта, а человек движется относительно поезда, т.е. любая скорость была относительна какой-то системе отсчёта. А из уравнений Максвелла следовало, что скорость света постоянна независимо от системы отсчёта.
В результате возникли попытки разрешить это противоречие с помощью теории эфира. Предполагалось, что свет и электромагнитные колебания распространяются в особой среде называемой эфиром. По мнению многих физиков уравнения Максвелла должны были быть модифицированы для наблюдателей движущихся относительно эфира.
Последовали многочисленные эксперименты, целью которых было обнаружение движения Земли относительно эфира. Наибольшую известность получили эксперименты Майкельсона и Морли, хотя они не были единственными. Несмотря на то, что сложность и точность экспериментов постоянно увеличивалась обнаружить движение Земли сквозь эфир не удалось. Скорость света действительно оказалась одинаковой во всех направлениях.
На этом теория эфира и закончилась бы, но её последователи не сдавались. Физики пришли к предположению, что для тел движущихся сквозь эфир время замедляется таким образом, что скорость света всегда видится одинаковой и они получили… формулы релятивистского замедления времени, сокращения длины, а также преобразования координат (преобразования Лоренца).
Однако вернёмся к Эйнштейну. Он подумал «Бог с ним, с эфиром. Что если скорость света действительно одинакова для всех наблюдателей и не зависит от системы отсчёта?». Из этого простого предположения с помощью смелых рассуждений и железной логики он и вывел теорию относительности.
Но нет, это предположение возникло не на пустом месте. Почти 50 лет после публикации уравнений Максвелла оно лежало у всех на виду. Просто, никто не отваживался поставить под сомнение авторитет Ньютона. Пока наконец этого не сделал Альберт Эйнштейн.
Ставьте палец вверх чтобы видеть в своей ленте больше статей о космосе и науке!
Подписывайтесь на мой канал здесь, а также на мой канал на youtube. Каждую неделю там выходят видео, где я отвечаю на вопросы о космосе, физике, футурологии и многом другом!
Besides Michelson and Morley experimental results, Einstein also considered the theoretical aspects.
It can be derived from Maxwell’s equations that the speed at which electromagnetic waves travel is: $c=left(epsilon_{0}mu_{0}right)^{-1/2}$.
Since light is an electromagnetic wave, that means that the speed of light is equal to the speed of the electromagnetic waves. $epsilon_{0}$ and $mu_{0}$ are properties of the vacuum and are constants, so $c$ will also be a constant.
Thus from Maxwell’s theory of electromagnetism alone we can already see that the speed of light in vacuum should be constant.
On the other hand, Galilean invariance tells us that the laws of motion have the same form in all inertial frames. There is no special inertial frame (as far as Newton’s laws are concerned).
Another key element here is Galilean transformation, which was the tool used for transforming from one inertial frame to another.
It can be easily seen that considering the first two elements to be valid:
- Maxwell’s theory of electromagnetism – speed of light is constant
- Galilean invariance – the laws of motion have the same form in all inertial frames
means that we can no longer apply the Galilean transformation, because otherwise we will get a contradiction. Thus at least one of these three “key elements” must be wrong.
- Maxwell’s theory of electromagnetism – speed of light is constant
- Galilean invariance – the laws of motion have the same form in all inertial frames
- Galilean transformation
It turned out that the last one (Galilean transformation) was wrong. Einstein considered the first two correct and built the special theory of relativity. The correct transformation from one inertial frame to another, in the assumption of the validity of the Maxwell’s theory and Galilean invariance, turns out to be Lorentz transformation
. It is nice to check that the Lorentz transformation does indeed reduce to the Galilean transformation in the $vll c$ limit. That’s why, in a sense, Galilean transformation is not wrong, but rather incomplete or a particular case. We can say that Galilean transformation needed to be generalized, and this was acomplished by introducing the invariance of the speed of light and maintaining the Galilean invariance.
How do Maxwell’s equations predict that the speed of light is constant
Maxwell’s equations in differential form:
$$tag{1}nablacdot mathbf{E}=frac{rho}{epsilon_{0}}label{1}$$
$$tag{2}nablacdot mathbf{B}=0label{2}$$
$$tag{3}nablatimesmathbf{E}=-frac{partial mathbf{B}}{partial t}label{3}$$
$$tag{4}nablatimes mathbf{B}=mu_{0}mathbf{J}+mu_{0}epsilon_{0}frac{partial mathbf{E}}{partial t}label{4}$$
We can try to derive a wave equation in vacuum. Since we are considering the vacuum, we do not have charge densities, so equation ($ref{1}$) becomes: $$tag{5}nablacdot mathbf{E}=0label{5}$$
In vacuum we do not have current densities either, so equation ($ref{4}$) becomes:
$$tag{6}nablatimes mathbf{B}=mu_{0}epsilon_{0}frac{partial mathbf{E}}{partial t}label{6}$$
Now if we apply the curl to equation ($ref{3}$), we get:
$$tag{7}nablatimesleft(nablatimesmathbf{E}right)=-frac{partial}{partial t}left(nablatimesmathbf{B}right)label{7}$$
We can use vector identity to evaluate the LHS of equation ($ref{7}$):
$$tag{8}nablatimesleft(nablatimesmathbf{E}right)=nablaleft(underbrace{nablacdotmathbf{E}}_{=0}right)-nabla^2mathbf{E}label{8}$$
$$tag{9}nablatimesleft(nablatimesmathbf{E}right)=-nabla^2mathbf{E}label{9}$$
For the RHS of equation ($ref{7}$), we can replace $nablatimesmathbf{B}$ with the expression we have from equation ($ref{6}$):
$$tag{10}-frac{partial}{partial t}left(nablatimesmathbf{B}right)=-frac{partial}{partial t}left(mu_{0}epsilon_{0}frac{partial mathbf{E}}{partial t}right)=-mu_{0}epsilon_{0}frac{partial^2 mathbf{E}}{partial t^2}label{10}$$
Putting all together:
$$tag{11}-nabla^2mathbf{E}=-mu_{0}epsilon_{0}frac{partial^2 mathbf{E}}{partial t^2}label{11}$$
$$tag{12}nabla^2mathbf{E}-mu_{0}epsilon_{0}frac{partial^2 mathbf{E}}{partial t^2}label{12}=0$$
The general form of a wave equation is:
$$tag{13}nabla^2mathbf{Psi}-frac{1}{v^2}frac{partial^2 mathbf{Psi}}{partial t^2}label{13}=0$$
where $v$ is the velocity of the wave.
Equation ($ref{12}$) decribes an electromagnetic wave moving with velocity $v=frac{1}{sqrt{epsilon_{0}mu_{0}}}$. Since light is an electromagnetic wave, that means that light is also propagating at this speed in vacuum. And since both $epsilon_{0}$ and $mu_{0}$ are constant, that means that $frac{1}{sqrt{epsilon_{0}mu_{0}}}$ is also a constant. Hence light moves at a constant speed in vacuum.

солнечному свету требуется в среднем[Прим. 1] 8 минут 17 секунд, чтобы достигнуть Земли |
|
| точные значения | |
|---|---|
| метров в секунду | 299 792 458 |
| Планковских единиц | 1 |
| приблизительные значения | |
| километров в секунду | 300 000 |
| километров в час | 1,08 млрд |
| астрономических единиц в сутки | 173 |
| приблизительное время путешествия светового сигнала | |
| расстояние | время |
| один метр | 3,3 нс |
| один километр | 3,3 мкс |
| от геостационарной орбиты до Земли | 119 мс |
| длина экватора Земли | 134 мс |
| от Луны до Земли | 1,255 с |
| от Солнца до Земли (1 а. е.) | 8,3 мин. |
| от Вояджера-1 до Земли | 22 часа 05 минут (на март 2023)[1] |
| один световой год | 1 год |
| один парсек | 3,26 лет |
| от Проксимы Центавра до Земли | 4,24 лет |
| от Альфы Центавра до Земли | 4,37 лет |
| от ближайшей галактики (Карликовой галактики в Большом Псе) до Земли | 25 000 лет |
| через Млечный Путь | 100 000 лет |
| от галактики Андромеды до Земли | 2,5 млн лет |
| от самой удалённой известной галактики до Земли | 13,4 млрд лет[2] |
Ско́рость све́та в вакууме[Прим. 2] — абсолютная величина скорости распространения электромагнитных волн, в точности равная 299 792 458 м/с (или приблизительно 3×108 м/с). В физике традиционно обозначается латинской буквой «
Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства геометрии пространства-времени в целом[3]. Из постулата причинности (любое событие может оказывать влияние только на события, происходящие позже него, и не может оказывать влияние на события, произошедшие раньше него[4][5][6]) и постулата специальной теории относительности о независимости скорости света в вакууме от выбора инерциальной системы отсчёта (скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга[7]) следует, что скорость любого сигнала и элементарной частицы не может превышать скорость света[8][9][6]. Таким образом, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.
В вакууме[править | править код]
![]()
Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 с
Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году[Прим. 3].
На данный момент считают, что скорость света в вакууме — фундаментальная физическая постоянная, по определению, точно равная 299 792 458 м/с, или 1 079 252 848,8 км/ч. Точность значения связана с тем, что с 1983 года метр в Международной системе единиц (СИ) определён как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[11].
В планковской системе единиц скорость света в вакууме равна 1. Можно сказать, что свет проходит 1 планковскую длину за планковское время, но в планковской системе единиц скорость света 
В природе со скоростью света распространяются (в вакууме):
Массивные частицы могут иметь скорость, приближающуюся почти вплотную к скорости света[Прим. 4], но всё же не достигающую её точно. Например, околосветовую скорость, лишь на 3 м/сек меньше скорости света, имеют массивные частицы (протоны), полученные на ускорителе (Большой адронный коллайдер) или входящие в состав космических лучей.[источник не указан 1987 дней]
В современной физике считается хорошо обоснованным утверждение, что причинное воздействие не может переноситься со скоростью, большей скорости света в вакууме (в том числе посредством переноса такого воздействия каким-либо физическим телом). Существует, однако, проблема «запутанных состояний» частиц, которые, судя по всему, «узнают» о состоянии друг друга мгновенно. Однако и в этом случае сверхсветовой передачи информации не происходит, поскольку для передачи информации таким способом необходимо привлечь дополнительный классический канал передачи со скоростью света[Прим. 5].
Хотя в принципе движение каких-то объектов со скоростью, большей скорости света в вакууме, вполне возможно, однако это могут быть, с современной точки зрения, только такие объекты, которые не могут быть использованы для переноса информации с их движением (например, солнечный зайчик в принципе может двигаться по стене со скоростью, большей скорости света, но никак не может быть использован для передачи информации с такой скоростью от одной точки стены к другой)[13]![]() .
.
В прозрачной среде[править | править код]
Скорость света в прозрачной среде — скорость, с которой свет распространяется в среде, отличной от вакуума. В среде, обладающей дисперсией, различают фазовую и групповую скорость.
Фазовая скорость связывает частоту и длину волны монохроматического света в среде (





Групповая скорость света определяется как скорость распространения биений между двумя волнами с близкой частотой и в равновесной среде всегда меньше 

Арман Ипполит Луи Физо на опыте доказал, что движение среды относительно светового луча также способно влиять на скорость распространения света в этой среде.
Вывод скорости света из уравнений Максвелла[править | править код]
Уравнения Максвелла в дифференциальной форме:























Для электромагнитной волны 



Согласно свойству ротора векторного поля 










Уравнение волны:





Подставляем (1) в (2), находим скорость:








В вакууме 


Фундаментальная роль в физике[править | править код]

Лоренц-фактор 


Скорость, с которой световые волны распространяются в вакууме, не зависит ни от движения источника волн, ни от системы отсчёта наблюдателя[Прим. 6]. Эйнштейн постулировал такую инвариантность скорости света в 1905 году[15]. Он пришёл к этому выводу на основании теории электромагнетизма Максвелла и доказательства отсутствия светоносного эфира[16].
Инвариантность скорости света неизменно подтверждается множеством экспериментов[17]. Существует возможность проверить экспериментально лишь то, что скорость света в «двустороннем» эксперименте (например, от источника к зеркалу и обратно) не зависит от системы отсчёта, поскольку невозможно измерить скорость света в одну сторону (например, от источника к удалённому приёмнику) без дополнительных договоренностей относительно того, как синхронизировать часы источника и приёмника. Однако, если применить для этого синхронизацию Эйнштейна, односторонняя скорость света становится равной двусторонней по определению[18][19].
Специальная теория относительности исследует последствия инвариантности 

Специальная теория относительности имеет много экспериментально проверенных последствий, которые противоречат интуиции[22]. Такие последствия включают: эквивалентность массы и энергии 

где 




Объединение результатов специальной теории относительности требует выполнения двух условий: (1) пространство и время являются единой структурой, известной как пространство-время (где 





Считается, что фундаментальные константы, такие как 
Кроме того, считается, что скорость света изотропна, то есть не зависит от направления его распространения. Наблюдения за излучением ядерных энергетических переходов как функции от ориентации ядер в магнитном поле (эксперимент Гугса — Древера), а также вращающихся оптических резонаторов (эксперимент Майкельсона — Морли и его новые вариации), наложили жёсткие ограничения на возможность двусторонней анизотропии[33][34].
В ряде естественных систем единиц скорость света является единицей измерения скорости[35]. В планковской системе единиц, также относящейся к естественным системам, она служит в качестве единицы скорости и является одной из основных единиц системы.
Верхний предел скорости[править | править код]
Согласно специальной теории относительности, энергия объекта с массой покоя 










Относительность одновременности возникающая при преобразованиях Лоренца. Три цветные системы отсчета связаны с тремя разными наблюдателями, движущимися относительно оси x. По отношению к зеленому наблюдателю красный движется со скоростью +0,28c, а синий с −0,52c. Пусть в ситеме отсчета зеленого наблюдателя событие «B» произошло одновременно с событием «A», тогда для синего событие «B» произойдет раньше, чем «A», а для красного наоборот — «A» раньше, чем «B».
Вообще информация или энергия не могут передаваться в пространстве быстрее, чем со скоростью света. Один из аргументов в пользу этого следует из контринтуитивного заключения специальной теории относительности, известного как относительность одновременности. Если пространственное расстояние между двумя событиями А и В больше, чем промежуток времени между ними, умноженный на 
История измерений скорости света[править | править код]
Античные учёные, за редким исключением, считали скорость света бесконечной[40]. В Новое время этот вопрос стал предметом дискуссий. Галилей и Гук допускали, что она конечна, хотя и очень велика, в то время как Кеплер, Декарт и Ферма по-прежнему отстаивали бесконечность скорости света.

Наблюдения при измерении скорости света при затмениях Ио Юпитером
Первую оценку скорости света произвёл Олаф Рёмер (1676). Он заметил, что, когда Земля на своей орбите находится дальше от Юпитера, затмения Юпитером спутника Юпитера Ио запаздывают по сравнению с расчётами на 22 минуты. Отсюда он получил значение для скорости света около 220 000 км/с — неточное значение, но близкое к истинному. В 1676 году он сделал сообщение в Парижской Академии, но не опубликовал свои результаты в виде формальной научной работы. Поэтому научное сообщество приняло идею о конечной скорости света только полвека спустя[41], когда в 1728 году открытие аберрации позволило Дж. Брэдли подтвердить конечность скорости света и уточнить её оценку. Полученное Брэдли значение составило 308 000 км/с[42][43].
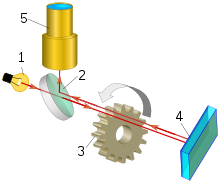
Схема опыта Физо по определению скорости света.
1 — Источник света.
2 — Светоделительное полупрозрачное зеркало.
3 — Зубчатое колесо-прерыватель светового пучка.
4 — Удалённое зеркало.
5 — Телескопическая труба.
Впервые измерения скорости света, основанные на определении времени прохождения светом точно измеренного расстояния в земных условиях, выполнил в 1849 году А. И. Л. Физо. В своих экспериментах Физо использовал разработанный им «метод прерываний», при этом расстояние, преодолеваемое светом в опытах Физо, составляло 8,63 км. Полученное в результате выполненных измерений значение оказалось равным 313 300 км/с.
В дальнейшем метод прерываний значительно усовершенствовали и его использовали для измерений М. А. Корню (1876 г.), А. Ж. Перротен (1902 г.) и Э. Бергштранд[sv]. Измерения, выполненные Э. Бергштрандом в 1950 году, дали для скорости света значение 299 793,1 км/с, при этом точность измерений была доведена до 0,25 км/с[42].
Другой лабораторный метод («метод вращающегося зеркала»), идея которого была высказана в 1838 году Ф. Араго, в 1862 году осуществил Леон Фуко. Измеряя малые промежутки времени с помощью вращающегося с большой скоростью (512 об/с) зеркала, он получил для скорости света значение 298 000 км/с с погрешностью 500 км/с. Длина базы в экспериментах Фуко была сравнительно небольшой — двадцать метров[43][42][44][45][46]. В последующем за счёт совершенствования техники эксперимента, увеличения используемой базы и более точного определения её длины точность измерений с помощью метода вращающегося зеркала была существенно повышена. Так, С. Ньюком в 1891 году получил значение 299 810 км/с с погрешностью 50 км/с, а А. А. Майкельсону в 1926 году удалось понизить погрешность до 4 км/с и получить для скорости величину 299 796 км/с. В своих экспериментах Майкельсон использовал базу, равную 35 373,21 м[42].
Дальнейший прогресс был связан с появлением мазеров и лазеров, которые отличаются очень высокой стабильностью частоты излучения, что позволило определять скорость света одновременным измерением длины волны и частоты их излучения. В начале 1970-х годов погрешность измерений скорости света приблизилась к 1 м/с[47]. После проверки и согласования результатов, полученных в различных лабораториях, XV Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с, с относительной погрешностью (неопределённостью) 4⋅10-9[48], что соответствует абсолютной погрешности 1,2 м/с[49].
Существенно, что дальнейшее повышение точности измерений стало невозможным в силу обстоятельств принципиального характера: ограничивающим фактором стала величина неопределённости реализации определения метра, действовавшего в то время. Проще говоря, основной вклад в погрешность измерений скорости света вносила погрешность «изготовления» эталона метра, относительное значение которой составляло 4⋅10-9[49]. Исходя из этого, а также учитывая другие соображения, XVII Генеральная конференция по мерам и весам в 1983 году приняла новое определение метра, положив в его основу рекомендованное ранее значение скорости света и определив метр как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1 / 299 792 458 секунды[50].
Сверхсветовое движение[править | править код]
Из специальной теории относительности следует, что превышение скорости света физическими частицами (массивными или безмассовыми) нарушило бы принцип причинности — в некоторых инерциальных системах отсчёта оказалась бы возможной передача сигналов из будущего в прошлое. Однако теория не исключает для гипотетических частиц, не взаимодействующих с обычными частицами[51], движение в пространстве-времени со сверхсветовой скоростью.
Гипотетические частицы, движущиеся со сверхсветовой скоростью, называются тахионами. Математически движение тахионов описывается преобразованиями Лоренца как движение частиц с мнимой массой. Чем выше скорость этих частиц, тем меньше энергии они несут, и наоборот, чем ближе их скорость к скорости света, тем больше их энергия — так же, как и энергия обычных частиц, энергия тахионов стремится к бесконечности при приближении к скорости света. Это самое очевидное следствие преобразования Лоренца, не позволяющее массивной частице (как с вещественной, так и с мнимой массой) достичь скорости света — сообщить частице бесконечное количество энергии просто невозможно.
Следует понимать, что, во-первых, тахионы — это класс частиц, а не один вид частиц, и во-вторых, тахионы не нарушают принцип причинности, если они никак не взаимодействуют с обычными частицами[51].
Обычные частицы, движущиеся медленнее света, называются тардионами. Тардионы не могут достичь скорости света, а только лишь сколь угодно близко подойти к ней, так как при этом их энергия становится неограниченно большой. Все тардионы обладают массой, в отличие от безмассовых частиц, называемых люксонами. Люксоны в вакууме всегда движутся со скоростью света, к ним относятся фотоны, глюоны и гипотетические гравитоны.
C 2006 года показано, что в так называемом эффекте квантовой телепортации кажущееся взаимовлияние частиц распространяется быстрее скорости света. Например, в 2008 г. исследовательская группа доктора Николаса Гизена (Nicolas Gisin) из университета Женевы, исследуя разнесённые на 18 км в пространстве запутанные фотонные состояния, показала, что это кажущееся «взаимодействие между частицами осуществляется со скоростью, примерно в сто тысяч раз большей скорости света». Ранее также обсуждался так называемый «парадокс Хартмана[en]» — кажущаяся сверхсветовая скорость при туннельном эффекте[52]. Анализ этих и подобных результатов показывает, что они не могут быть использованы для сверхсветовой передачи какого-либо несущего информацию сообщения или для перемещения вещества[53].
В результате обработки данных эксперимента OPERA[54], набранных с 2008 по 2011 год в лаборатории Гран-Сассо совместно с ЦЕРН, было зафиксировано статистически значимое указание на превышение скорости света мюонными нейтрино[55]. Сообщение об этом сопровождалось публикацией в архиве препринтов[56]. Полученные результаты специалисты подвергли сомнению, поскольку они не согласуются не только с теорией относительности, но и с другими экспериментами с нейтрино[57]. В марте 2012 года в том же тоннеле были проведены независимые измерения, и сверхсветовых скоростей нейтрино они не обнаружили[58]. В мае 2012 года OPERA провела ряд контрольных экспериментов и пришла к окончательному выводу, что причиной ошибочного предположения о сверхсветовой скорости стал технический дефект (плохо вставленный разъём оптического кабеля)[59].
См. также[править | править код]
- Переменная скорость света
- Односторонняя скорость света
- Световой год
- Скорость звука
- Планковские единицы
- Рациональная система единиц
Примечания[править | править код]
- Комментарии
- ↑ От поверхности Солнца — от 8 мин 8,3 с в перигелии до 8 мин 25 с в афелии.
- ↑ Скорость распространения светового импульса в среде отличается от скорости его распространения в вакууме (меньше, чем в вакууме), и может быть различной для разных сред. Когда говорят просто о скорости света, обычно подразумевается именно скорость света в вакууме; если же говорят о скорости света в среде, это, как правило, оговаривается явно.
- ↑ В настоящее время наиболее точные методы измерения скорости света основаны на независимом определении значений длины волны
и частоты
света или другого электромагнитного излучения и последующего расчёта в соответствии с равенством
[10].
- ↑ См. например «Частица Oh-My-God».
- ↑ Аналогом может быть посылка наудачу двух заклеенных конвертов с белой и чёрной бумагой в разные места. Открытие одного конверта гарантирует, что во втором будет лежать второй лист — если первый чёрный, то второй белый, и наоборот. Эта «информация» может распространяться быстрее скорости света — ведь вскрыть второй конверт можно в любое время, и там всегда будет этот второй лист. При этом принципиальная разница с квантовым случаем состоит только в том, что в квантовом случае до «открытия конверта»-измерения состояние листа внутри принципиально неопределённо, как у кота Шрёдингера, и там может оказаться любой лист.
- ↑ Однако частота света зависит от движения источника света относительно наблюдателя, благодаря эффекту Доплера.
- ↑ Помимо того, что измеряемые движущиеся объекты оказываются короче вдоль линии относительного движения, они также выглядят повёрнутыми. Этот эффект, известный как вращение Террелла, связан с разницей во времени между пришедшими к наблюдателю сигналами от разных частей объекта[23][24].
- ↑ Считается, что эффект Шарнхорста позволяет сигналам распространяться немногим выше
, но особые условия, при которых эффект может возникать, мешают применить этот эффект для нарушения принципа причинности[37].
- Источники
- ↑ Where Are the Voyagers – NASA Voyager. Voyager – The Interstellar Mission. Jet Propulsion Laboratory, California Istitute of Technology. Дата обращения: 12 июля 2011. Архивировано 3 февраля 2012 года.
- ↑ Amos, Jonathan. Hubble sets new cosmic distance record, BBC News (3 марта 2016). Архивировано 4 марта 2016 года. Дата обращения: 3 марта 2016.
- ↑ 1 2 Is The Speed of Light Everywhere the Same? Дата обращения: 10 сентября 2015. Архивировано 8 сентября 2015 года.
- ↑ Начала теоретической физики, 2007, с. 169.
- ↑ Неванлинна, 1966, с. 122.
- ↑ 1 2 Чудинов Э. М. Теория относительности и философия. — М.: Политиздат, 1974. — С. 222—227.
- ↑ Эволюция физики, 1948, с. 167.
- ↑ Начала теоретической физики, 2007, с. 170.
- ↑ Неванлинна, 1966, с. 184.
- ↑ Сажин М. В. Скорость света // Физика космоса : маленькая энциклопедия / Гл. ред. Р. А. Сюняев. — Изд. 2-е, перераб. и доп. — М.: Советская энциклопедия, 1986. — С. 622. — 783 с. — 70 000 экз.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. Дата обращения: 14 августа 2012. Архивировано из оригинала 10 ноября 2012 года.
- ↑ Abbott B. P. et al. (LIGO Scientific Collaboration, Virgo Collaboration, Fermi Gamma-ray Burst Monitor, and INTEGRAL). Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A // The Astrophysical Journal. — 2017. — Vol. 848. — P. L13. — doi:10.3847/2041-8213/aa920c. [исправить]
- ↑ Болотовский Б. М., Гинзбург В. Л. Эффект Вавилова — Черенкова и эффект Допплера при движении источников со скоростью больше скорости света в вакууме // Успехи физических наук. — Российская академия наук, 1972. — Т. 106, № 4. — С. 577—592. Архивировано 25 сентября 2013 года.
- ↑ Миллер М. А., Суворов E. В. Групповая скорость // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 544—545. — 704 с.
- ↑ Stachel, J. J. Einstein from “B” to “Z” – Volume 9 of Einstein studies (нем.). — Springer, 2002. — S. 226. — ISBN 0-8176-4143-2. Архивная копия от 16 ноября 2016 на Wayback Machine
- ↑ Einstein, A. Zur Elektrodynamik bewegter Körper (нем.) // Annalen der Physik. — 1905. — Bd. 17. — S. 890—921. — doi:10.1002/andp.19053221004. English translation: Perrett, W; Jeffery, GB (tr.); Walker, J (ed.) On the Electrodynamics of Moving Bodies. Fourmilab. Дата обращения: 27 ноября 2009. Архивировано 1 февраля 2013 года.
- ↑ Александров Е. Б. Теория относительности: прямой эксперимент с кривым пучком // Химия и жизнь. — 2012. — № 3. Архивировано 4 марта 2016 года.
- ↑
Hsu, J-P; Zhang, Y. Z. Lorentz and Poincaré Invariance. — World Scientific, 2001. — Т. 8. — С. 543ff. — (Advanced Series on Theoretical Physical Science). — ISBN 981-02-4721-4. - ↑ 1 2 Zhang, Y. Z. Special Relativity and Its Experimental Foundations (англ.). — World Scientific, 1997. — Vol. 4. — P. 172—173. — (Advanced Series on Theoretical Physical Science). — ISBN 981-02-2749-3. Архивная копия от 19 мая 2012 на Wayback Machine Архивированная копия. Дата обращения: 24 января 2013. Архивировано из оригинала 19 мая 2012 года.
- ↑
d’Inverno, R. Introducing Einstein’s Relativity (англ.). — Oxford University Press, 1992. — P. 19—20. — ISBN 0-19-859686-3. - ↑
Sriranjan, B. Postulates of the special theory of relativity and their consequences // The Special Theory to Relativity. — PHI Learning, 2004. — С. 20 ff. — ISBN 81-203-1963-X. - ↑ Roberts, T; Schleif, S; Dlugosz, JM (ed.) What is the experimental basis of Special Relativity? Usenet Physics FAQ. University of California, Riverside (2007). Дата обращения: 27 ноября 2009. Архивировано 1 февраля 2013 года.
- ↑
Terrell, J. Invisibility of the Lorentz Contraction (англ.) // Physical Review : journal. — 1959. — Vol. 116, no. 4. — P. 1041—1045. — doi:10.1103/PhysRev.116.1041. — Bibcode: 1959PhRv..116.1041T. - ↑
Penrose, R. The Apparent Shape of a Relativistically Moving Sphere (англ.) // Proceedings of the Cambridge Philosophical Society (англ.) (рус. : journal. — 1959. — Vol. 55, no. 01. — P. 137—139. — doi:10.1017/S0305004100033776. — Bibcode: 1959PCPS…55..137P. - ↑
Hartle, J. B. Gravity: An Introduction to Einstein’s General Relativity (англ.). — Addison-Wesley, 2003. — P. 52—9. — ISBN 981-02-2749-3. - ↑
Hartle, J. B. Gravity: An Introduction to Einstein’s General Relativity (англ.). — Addison-Wesley, 2003. — P. 332. — ISBN 981-02-2749-3. - ↑ The interpretation of observations on binary systems used to determine the speed of gravity is considered doubtful by some authors, leaving the experimental situation uncertain; seeSchäfer, G; Brügmann, M. H. Propagation of light in the gravitational filed of binary systems to quadratic order in Newton’s gravitational constant: Part 3: ‘On the speed-of-gravity controversy’ // Lasers, clocks and drag-free control: Exploration of relativistic gravity in space (англ.) / Dittus, H; Lämmerzahl, C; Turyshev, S. G.. — Springer, 2008. — ISBN 3-540-34376-8.
- ↑ Gibbs, P Is The Speed of Light Constant? Usenet Physics FAQ. University of California, Riverside (1997). Дата обращения: 26 ноября 2009. Архивировано 17 ноября 2009 года.
- ↑
Ellis, GFR; Uzan, J-P. ‘c’ is the speed of light, isn’t it? (англ.) // American Journal of Physics : journal. — 2005. — Vol. 73, no. 3. — P. 240—247. — doi:10.1119/1.1819929. — Bibcode: 2005AmJPh..73..240E. — arXiv:gr-qc/0305099.. — «The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.». - ↑ An overview can be found in the dissertation of Mota, DF (2006), Variations of the fine structure constant in space and time, arΧiv:astro-ph/0401631 [astro-ph].
- ↑
Uzan, J-P. The fundamental constants and their variation: observational status and theoretical motivations (англ.) // Reviews of Modern Physics : journal. — 2003. — Vol. 75, no. 2. — P. 403. — doi:10.1103/RevModPhys.75.403. — Bibcode: 2003RvMP…75..403U. — arXiv:hep-ph/0205340. - ↑
Amelino-Camelia, G (2008), Quantum Gravity Phenomenology, arΧiv:0806.0339 [gr-qc]. - ↑ Herrmann, S; Senger, A; Möhle, K; Nagel, M; Kovalchuk, EV; Peters, A. Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level (англ.) // Physical Review D : journal. — 2009. — Vol. 80, no. 100. — P. 105011. — doi:10.1103/PhysRevD.80.105011. — Bibcode: 2009PhRvD..80j5011H. — arXiv:1002.1284.
- ↑ Lang, K. R. Astrophysical formulae. — 3rd. — Birkhäuser (англ.) (рус., 1999. — С. 152. — ISBN 3-540-29692-1.
- ↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.
- ↑ Fowler, M Notes on Special Relativity 56. University of Virginia (март 2008). Дата обращения: 7 мая 2010. Архивировано 1 февраля 2013 года.
- ↑
Liberati, S; Sonego, S; Visser, M. Faster-than-c signals, special relativity, and causality (англ.) // Annals of Physics (англ.) (рус. : journal. — 2002. — Vol. 298, no. 1. — P. 167—185. — doi:10.1006/aphy.2002.6233. — Bibcode: 2002AnPhy.298..167L. — arXiv:gr-qc/0107091. - ↑
Taylor, EF; Wheeler, J. A. Spacetime Physics. — W. H. Freeman (англ.) (рус., 1992. — С. 74—5. — ISBN 0-7167-2327-1. - ↑
Tolman, R. C. Velocities greater than that of light // The Theory of the Relativity of Motion. — Reprint. — BiblioLife (англ.) (рус., 2009. — С. 54. — ISBN 978-1-103-17233-7. - ↑ Гиндикин С. Г. Рассказы о физиках и математиках. — издание третье, расширенное. — М.: МЦНМО, 2001. — С. 105—108. — ISBN 5-900916-83-9. Архивная копия от 11 июля 2020 на Wayback Machine
- ↑ Стюарт, 2018, с. 178.
- ↑ 1 2 3 4 Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 384—389. — 848 с. — ISBN 5-9221-0314-8.
- ↑ 1 2 Бонч-Бруевич А. М. Скорость света // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 548—549. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Léon Foucault. Détermination expérimentale de la vitesse de la lumière ; description des appareils (фр.) // Comptes rendus hebdomadaires des séances de l’Académie des Sciences. — Paris, 1862. — Vol. 55. — P. 792—796. Архивировано 24 сентября 2015 года.
- ↑ Léon Foucault. Détermination expérimentale de la vitesse de la lumière ; parallaxe du Soleil (фр.) // Comptes rendus hebdomadaires des séances de l’Académie des Sciences. — Paris, 1862. — Vol. 55. — P. 501—503. Архивировано 24 сентября 2015 года.
- ↑ Léon Foucault. Experimental Determination of the Velocity of Light: Description of the Apparatus (англ.) // Philosophical Magazine. Fourth Series. — London, 1863. — Vol. 25. — P. 76—79.
- ↑ Evenson K. M., Wells J. S., Petersen F. R., Danielson B. L., Day G. W. Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser (англ.) // Phys. Rev. Lett.. — 1972. — Vol. 29, no. 19. — P. 1346—1349. — doi:10.1103/PhysRevLett.29.1346.
- ↑ Указанная погрешность представляет собой утроенное стандартное отклонение.
- ↑ 1 2 Рекомендованное значение скорости света Архивная копия от 7 октября 2008 на Wayback Machine (англ.) Резолюция 2 XV Генеральной конференции по мерам и весам (1975)
- ↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
- ↑ 1 2 Введение в рассмотрение полевой квантовой природы этих сверхсветовых частиц, возможно, позволяет обойти это ограничение через принцип переинтерпретации наблюдений.
- ↑ Давидович М. В. О парадоксе Хартмана, туннелировании электромагнитных волн и сверхсветовых скоростях // Успехи физических наук. — М.: Российская академия наук, 2009 (апрель). — Вып. 179. — С. 443. Архивировано 24 октября 2020 года.
- ↑ И. Иванов. Проведены новые эксперименты по проверке механизма квантовой запутанности. Архивная копия от 31 августа 2008 на Wayback Machine Элементы.ру.
- ↑ Oscillation Project with Emulsion-tRacking Apparatus. Дата обращения: 23 сентября 2011. Архивировано 11 октября 2012 года.
- ↑ OPERA experiment reports anomaly in flight time of neutrinos from CERN to Gran Sasso. Дата обращения: 10 января 2016. Архивировано 5 апреля 2013 года.
- ↑ OPERA Collaboration (Adam T. et al.) (2011), Measurement of the neutrino velocity with the OPERA detector in the CNGS beam, arΧiv:1109.4897..
- ↑ И.Иванов. Эксперимент OPERA сообщает о наблюдении сверхсветовой скорости нейтрино. Архивная копия от 25 сентября 2012 на Wayback Machine Элементы.ру, 23 сентября 2011 года.
- ↑ ICARUS Collaboration et al. Measurement of the neutrino velocity with the ICARUS detector at the CNGS beam // Physics Letters B. — 2012. — Vol. 713 (18 июля). — P. 17–22. — arXiv:1203.3433. — doi:10.1016/j.physletb.2012.05.033.
- ↑ Эксперимент OPERA окончательно «закрыл» сверхсветовые нейтрино Архивная копия от 7 июля 2012 на Wayback Machine.
Литература[править | править код]
- Александров Е. Б., Александров П. А., Запасский В. С., Корчуганов В. Н., Стирин А. И. Эксперименты по прямой демонстрации независимости скорости света от скорости движения источника // Успехи физических наук. — Российская академия наук, 2011. — Вып. 12.
- Физические величины: Справочник./А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др.; под ред. И. С. Григорьева, Е. З. Мейлихова М.: Энергоатомиздат, 1991, — 1232 с.— ISBN 5-283-04013-5.
- Эйнштейн А., Инфельд Л. Эволюция физики. — М.: ОГИЗ, 1948. — 267 с.
- Медведев Б. В. Начала теоретической физики. — М.: Физматлит, 2007. — 600 с.
- Неванлинна Р. Пространство, время и относительность. — М.: Мир, 1966. — 229 с.
- Иэн Стюарт. Математика космоса. Как современная наука расшифровывает Вселенную = Stewart Ian. Calculating the Cosmos: How Mathematics Unveils the Universe. — Альпина Паблишер, 2018. — 542 p. — ISBN 978-5-91671-814-0.
- И.В.Савельев “Курс общей физики” том II
Ссылки[править | править код]
- Скорость света — статья в Физической энциклопедии
- Скорость света на astronet.ru
- Rømer, O (1676). “Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l’Academie Royale des Sciences” (PDF). Journal des sçavans [фр.]: 223—36.
- Halley, E (1694). “Monsieur Cassini, his New and Exact Tables for the Eclipses of the First Satellite of Jupiter, reduced to the Julian Stile and Meridian of London”. Philosophical Transactions of the Royal Society. 18 (214): 237—56. Bibcode:1694RSPT…18..237C. DOI:10.1098/rstl.1694.0048.
- Fizeau, HL (1849). “Sur une expérience relative à la vitesse de propagation de la lumière” (PDF). Comptes rendus de l’Académie des sciences [фр.]. 29: 90—92, 132.
- Foucault, JL (1862). “Détermination expérimentale de la vitesse de la lumière: parallaxe du Soleil”. Comptes rendus de l’Académie des sciences [фр.]. 55: 501—03, 792—96.
Кто бы мог подумать, что мелкий почтовый служащий изменит основы науки своего времени? Но такое случилось! Теория относительности Эйнштейна заставила пересмотреть привычный взгляд на устройство Вселенной и открыла новые области научного познания.
Большинство научных открытий сделано с помощью эксперимента: ученые повторяли свои опыты много раз, чтобы быть уверенными в их результатах. Работы обычно проводились в университетах или исследовательских лабораториях больших компаний.
Альберт Эйнштейн полностью изменил научную картину мира, не проведя ни одного практического эксперимента. Его единственными инструментами были бумага и ручка, а все эксперименты он проводил в голове.
Движущийся свет
В 1905 году Альберт Эйнштейн опубликовал свои первые статьи. В них шла речь о движении со скоростью, близкой к скорости света. Выдвинутая им теория получила название специальной теории относительности.

Альберт Эйнштейн (1879—1955) основывал все свои выводы но результатах «мысленного эксперимента». Эти эксперименты можно было совершить только в воображении.
Скорости всех движущихся тел относительны. Это означает, что все объекты движутся или остаются неподвижными только относительно какого-либо другого объекта. Например, человек, неподвижный относительно Земли, в то же время вращается вместе с Землей вокруг Солнца. Или допустим, что по вагону движущегося поезда идет человек в сторону движения со скоростью 3 км/час. Поезд движется со скоростью 60 км/час. Относительно неподвижного наблюдателя на земле скорость человека будет равна 63 км/час – скорость человека плюс скорость поезда. Если бы он шел против движения, то его скорость относительно неподвижного наблюдателя была бы равна 57 км/час.
Эйнштейн утверждал, что о скорости света так рассуждать нельзя. Скорость света всегда постоянна, независимо от того, приближается ли источник света к вам, удаляется от вас или стоит на месте.
Чем быстрее, тем меньше
С самого начала Эйнштейн выдвинул несколько удивительных предположений. Он утверждал, что, если скорость объекта приближается к скорости света, его размеры уменьшаются, а масса, наоборот, увеличивается. Никакое тело нельзя разогнать до скорости равной или большей скорости света.
Другой его вывод был еще удивительней и, казалось, противоречил здравому смыслу. Представьте, что из двоих близнецов один остался на Земле, а другой путешествовал по космосу со скоростью, близкой к скорости света. С момента старта на Земле прошло 70 лет. Согласно теории Эйнштейна, на борту корабля время течет медленнее, и там прошло, например, только десять лет. Получается, что тот из близнецов, кто оставался на Земле, стал на шестьдесят лет старше второго. Этот эффект называют «парадоксом близнецов». Звучит просто невероятно, но лабораторные эксперименты подтвердили, что замедление времени при скоростях, близких к скорости света, действительно существует.
Беспощадный вывод
Теория Эйнштейна также включает известную формулу E=mc2, в которой E – энергия, m – масса, а c – скорость света. Эйнштейн утверждал, что масса может превращаться в чистую энергию. В результате применения этого открытия в практической жизни появились атомная энергетика и ядерная бомба.

Эйнштейн был теоретиком. Эксперименты, которые должны были доказать правоту его теории, он оставлял другим. Многие из этих экспериментов было невозможно проделать до тех пор, пока не появились достаточно точные измерительные приборы.
Факты и события
- Был произведен следующий эксперимент: самолет, на котором были установлены очень точные часы, взлетел и, облетев с большой скоростью вокруг Земли, опустился в той же точке. Часы, находившиеся на борту самолета, на ничтожную долю секунды отстали от часов, которые оставались на Земле.
- Если в лифте, падающем с ускорением свободного падения, уронить шар, то шар не будет падать, а как бы зависнет в воздухе. Это происходит потому, что шар и лифт падают с одинаковой скоростью.
- Эйнштейн доказал, что тяготение влияет на геометрические свойства пространства-времени, которое в свою очередь влияет на движение тел в этом пространстве. Так, два тела, начавшие движение параллельно друг другу, в конце концов встретятся в одной точке.
Искривляя время и пространство
Десятью годами позже, в 1915—1916 годах, Эйнштейн построил новую теорию гравитации, названную им общей теорией относительности. Он утверждал, что ускорение (изменение скорости) действует на тела так же, как и сила гравитации. Космонавт не может по своим ощущениям определить, притягивает ли его большая планета, или ракета начала тормозить.
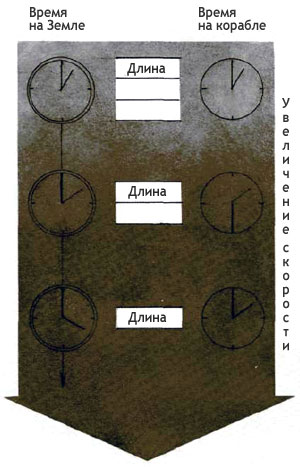
Если космический корабль разгоняется до скорости, близкой к скорости света, то часы на нем замедляются. Чем быстрее движется корабль, тем медленнее идут часы.
Отличия ее от ньютоновской теории тяготения проявляются при изучении космических объектов с огромной массой, например планет или звезд. Эксперименты подтвердили искривление лучей света, проходящих вблизи тел с большой массой. В принципе возможно столь сильное гравитационное поле, что свет не сможет выйти за его пределы. Это явление получило название «черной дыры». «Черные дыры», по-видимому, обнаружены в составе некоторых звездных систем.
Ньютон утверждал, что орбиты планет вокруг Солнца фиксированы. Теория Эйнштейна предсказывает медленный дополнительный поворот орбит планет, связанный с наличием гравитационного поля Солнца. Предсказание подтвердилось экспериментально. Это было поистине эпохальное открытие. В закон всемирного тяготения сэра Исаака Ньютона были внесены поправки.
Начало гонки вооружений
Работы Эйнштейна дали ключ ко многим тайнам природы. Они оказали влияние на развитие многих разделов физики, от физики элементарных частиц до астрономии – науки о строении Вселенной.
Эйнштейн в своей жизни занимался не только теорией. В 1914 году он стал директором института физики в Берлине. В 1933 году, когда к власти в Германии пришли нацисты, ему, как еврею, пришлось уехать из этой страны. Он переехал в США.
В 1939 году, несмотря на то что он был противником войны, Эйнштейн написал президенту Рузвельту письмо, в котором предупреждал его, что можно сделать бомбу, обладающую огромной разрушительной силой, и что фашистская Германия уже приступила к разработке такой бомбы. Президент отдал распоряжение начать работы. Это положило начало гонке вооружений.
Как понять теорию относительности
О том, как в знаменитой теории Альберта Эйнштейна взаимосвязаны скорость света, масса, время и пространство.

Как известно, вся материальная Вселенная имеет три измерения: вверх-вниз, вправо-влево, вперёд-назад. Четвёртое измерение — это время. Вместе они и составляют пространственно-временной континуум. Но вся загвоздка в том, что наши представления о пространстве и времени напрямую зависят от скорости, с которой мы движемся.
Именно взаимоотношения между временем, пространством и движущимся объектом описывает специальная теория относительности (СТО), разработанная Альбертом Эйнштейном в 1905 году. Позже на её основе великий физик создал также общую теорию относительности (ОТО), которая, помимо времени и пространства, учитывает и другие факторы, например гравитацию. О ней мы говорить не будем — для этого потребовался бы отдельный научный труд. Итак, приступим к изучению специальной теории относительности!
Главные принципы теории относительности
Первое, что нужно понять для освоения теории относительности: движение относительно.
Это значит, что наличие или отсутствие движения всегда определяется относительно других объектов. Движение и его скорость зависят от наблюдателя (того, кто смотрит на объект) и системы отсчёта (того, откуда он смотрит).
Представьте, что пассажир едет в поезде и читает книгу. Для него книга неподвижна, как неподвижны и кресла в поезде, и другие пассажиры (если они сидят на своих местах, а не пробираются к вагону-ресторану, конечно). Скорость всех неподвижных объектов в поезде, с точки зрения нашего пассажира-читателя, будет равна нулю.
В это время на платформе стоит другой человек, мимо которого со свистом пролетает поезд. Для него и пассажир с книгой, и кресла движутся со скоростью поезда — допустим, 200 км/ч. А вот пассажиры на пути в вагон-ресторан, расположенный в голове состава, будут двигаться ещё быстрее: их скорость сложится со скоростью поезда.
Так происходит при любом сложении скоростей, но есть одно исключение: скорость света. Свет от прожектора на носу нашего поезда будет двигаться всегда с одинаковой скоростью — 300 000 км/с.
Здесь мы вплотную подошли к базовым принципам, на которых строится теория относительности:
- Принцип относительности: для тех тел, которые относительно друг друга движутся на постоянной скорости или неподвижны (как пассажир и его книга), физические процессы протекают одинаково.
- Принцип постоянства скорости света: скорость света постоянна для всех наблюдателей, независимо от их скорости по отношению к источнику света. То есть свет от фонаря на носу поезда или свет от прожектора на космическом корабле имеют одинаковую скорость.
Свет движется так быстро, что его распространение кажется нам мгновенным. Но на космических расстояниях всё выглядит совсем по-другому. К примеру, расстояние от Солнца до Земли, составляющее 150 миллионов километров, свет проходит примерно за 8 минут. А значит, что если Солнце когда-нибудь потухнет, то мы увидим это только через 8 минут.
Следствия теории относительности
Что же следует из описанных выше принципов и как они связаны со временем и пространством? Теория относительности имеет три основных следствия: пространство расширяется, время сжимается, масса увеличивается. Разберёмся с каждым по порядку.
Время сжимается
Эйнштейн первым понял, что время не абсолютно и зависит от системы отсчёта, в которой мы его наблюдаем. Земля и далёкая галактика на другом конце Вселенной находятся в разных точках не только пространства, но и времени.
Относительно движущихся объектов время идёт медленнее. Этот факт был проверен с использованием двух одинаковых атомных часов: один прибор оставили на Земле, а другой отправили на сверхзвуковом самолёте вокруг планеты. При посадке было отмечено, что часы, которые летали, на несколько тысячных секунды отстают от часов в состоянии покоя.
Чем ближе скорость объекта становится к скорости света, тем медленнее для него течёт время. В теории, если астронавт отправится в путешествие на космическом корабле со скоростью, близкой к скорости света, он попадёт в будущее. Для него пройдёт несколько недель, а на Земле — несколько десятилетий. Это и есть относительность времени.
Пространство сжимается
Ещё одно удивительное следствие относительности: когда мы видим объект в движении, то можем наблюдать, что он становится всё более коротким с увеличением его скорости. С точки зрения наблюдателя, при приближении к скорости света объект становится всё короче и короче по направлению движения, а перпендикулярно ему остаётся в прежних размерах.
Допустим, мы сажаем астронавта в космический корабль, который может двигаться со скоростью света, а сами отправляемся в уютную обсерваторию наблюдать за его путешествием. По мере приближения к скорости света с кораблём начнёт происходить что-то странное. Мы заметим, что он становится всё короче. Но изменения происходят только в отношении направления движения, ширина корабля остаётся постоянной. Достигнув скорости света, он станет практически неразличим в длину.
Наверное, нашему астронавту сейчас не очень весело? Не беспокойтесь за него: для астронавта никаких изменений не происходит. Он всё так же радостно несётся навстречу космическим просторам и ничего не замечает. Пространство сжимается только относительно наблюдателя.
Масса увеличивается
Ещё одним поразительным следствием относительности является то, что по мере увеличения скорости объекта его масса тоже увеличивается.
Масса и энергия неразрывно связаны. Именно это выразил Эйнштейн в знаменитом уравнении E = mc². Эта формула показывает, что энергия тела пропорциональна его массе. При передаче телу энергии (то есть его ускорении) увеличивается и масса. Выходит, что часть энергии идёт на увеличение скорости, а другая часть увеличивает массу.
Вспомним о нашем астронавте, который приближается к скорости света в своём корабле. Наблюдая с Земли, мы видим, что по мере увеличения скорости корабля становится всё труднее ускорить его, то есть всё больше и больше энергии требуется, чтобы его подтолкнуть. Наступает момент, когда корабль достигнет такой массы, что никакая энергия во Вселенной больше не сможет его двигать. Вот поэтому на практике путешествия во времени пока невозможны.
Если коротко
Итак, при приближении к скорости света время расширяется, пространство сжимается. Но происходит всё это только в глазах наблюдателя, который видит движение объекта относительно себя. Для астронавта в корабле ничего не меняется (кроме увеличения массы). Но при этом обе точки зрения верны. Поэтому теория относительности и носит такое название.
Все ещё не очень ясно? Неудивительно, ведь самому Эйнштейну потребовалось 10 лет, чтобы сформировать основные постулаты теории относительности. Есть книга, которая поможет вам ещё раз уложить эти принципы в голове и объяснит всё буквально на пальцах, с яркими картинками и доступными графиками. «Теория относительности» от редакции «Аванта» издательства АСТ адресована школьникам средних классов, но будет интересна любому взрослому, желающему проникнуть в тайны нашей Вселенной. Ведь то, что кажется чудесами, на самом деле реальность!
Купить книгу

