Как фалес нашел высоту пирамиды

Приветствую Вас, уважаемые Читатели! Сегодня речь пойдет о замечательной теореме, с которой Вы должны были познакомиться еще в школе.

Её автор – древнегреческий философ Фалес Милетский, считающийся “отцом мудрецов” и основоположником античной мысли.

Личность Фалеса окутана тайной, ведь он жил за несколько столетий до Геродота и Аристотеля, в трудах которых и появилось первое упоминание о древнем мудреце.

По мнению некоторых ученых речь вообще идёт о «культурной легенде» — вымышленном или реальном человеке, с которым древние греки ассоциировали открытия и мысли своих предков до того момента, как появилась их письменная фиксация

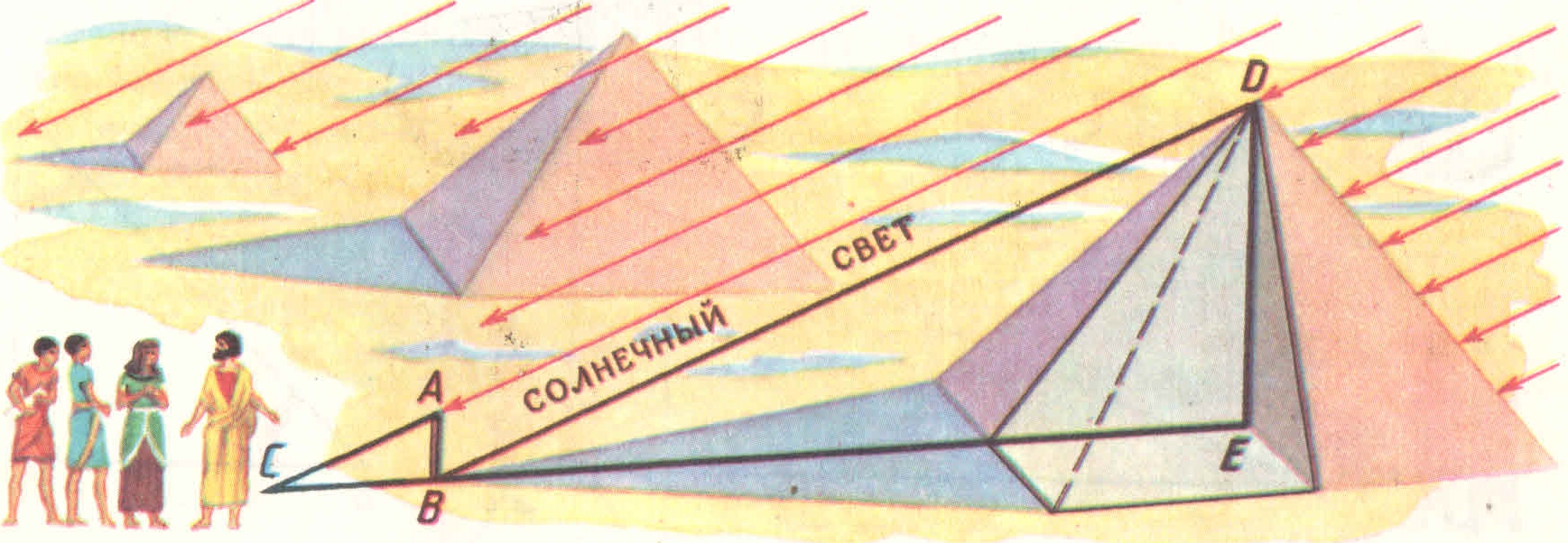
Согласно легенде, именно Фалес измерил высоту Пирамиды Хеопса, измеряя длину её тени в солнечный день.

Пониманию процесса и поможет одноименная теорема:

Теорема Фалеса (о пропорциональных отрезках)

Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Теорема Фалеса проста в доказательстве и является обобщенным случаем теоремы о пропорциональных отрезках (если считать равные отрезки на рисунке выше пропорциональными с коэффициентом 1):

Кстати, по школе помню, что отношение к теореме Фалеса такое, что в большинстве задач по геометрии, которые решались в рамках обычной школьной подготовки, эту теорему практически никогда не было необходимости применять.

Я сейчас говорю лично о своих школьных воспоминаниях. Поправьте, если сейчас это не так.

Ну а что же с пирамидой Хеопса?

Лучи света от удаленного источника (Солнца) можно считать параллельными. Тогда, зная высоту палки, а также отбрасываемую ей и пирамидой тень, по простому отношению можно вычислить и высоту архитектурного шедевра египтян.

Спасибо за внимание! Ставьте “Нравится” этой публикации и подписывайтесь на канал!

Читайте также:

Обновлено: 18.05.2023

Самый легкий и самый древний способ — без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего по тени высоту огромного сооружения.

Фалес, — говорит предание, — избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени. Вот, пожалуй, единственный случай, когда человек извлекает пользу из своей тени…

Задача греческого мудреца представляется нам теперь детски-простой, но не будем забывать, что смотрим мы на неё с высоты геометрического здания, воздвигнутого уже после Фалеса. Он жил задолго до Евклида, автора замечательной книги, по которой обучались геометрии в течение двух тысячелетий после его смерти. Заключенные в ней истины, известные теперь каждому школьнику, не были еще открыты в эпоху Фалеса. А чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес сам открыл):

1) что углы при основании равнобедренного треугольника равны, и обратно—что стороны, лежащие против равных углов треугольника, равны между собою;

2) что сумма углов всякого треугольника (или, по крайней мере, прямоугольного) равна двум прямым углам.

Только вооруженный этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды, середина ее основания и конец ее тени должны обозначить равнобедренный треугольник. Этим простым способом очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних.

Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда.

Нетрудно, однако, изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, кроме того, и свою тень или тень какого-нибудь шеста, вычисляют искомую высоту из пропорции (рис. 1):

т. е. высота дерева во столько же раз больше вашей собственной высоты (или высоты шеста), во сколько раз тень дерева длиннее вашей тени (или тени шеста). Это вытекает, конечно, из геометрического подобия треугольников ABC и аbc(по двум углам).

Когда вспоминают об основоположнике греческой науки и философии – Фалесе Милетском, обязательно, наряду с теоремой Фалеса об отрезках, отсекаемых параллельными на сторонах угла, вспоминают и остроумный способ определения высоты пирамиды Хеопса. Разные авторы пишут разное, но все сходятся в том, что он проводил одно измерение длины тени пирамиды и одно – тени шеста или тени своего тела. Почему-то при этом считается, что длину тени пирамиды легко измерить. А ведь это по условиям легенды невозможно. Как добраться до проекции вершины на плоскость основания, не производя никаких измерений самой пирамиды?

Я предлагаю некий фантастический рассказ о том, как же всё это происходило. На историческую достоверность, разумеется, не претендую.

С утра у великой пирамиды Хуфу выстроилась стража. В полдень ожидали Амасиса и жрецов. Начальник стражи, поседевший в битвах грек-наёмник, сражавшийся под водительством фараона тогда, когда тот ещё и
фараоном не был, недовольно разглядывал своего соотечественника. Впрочем, тот и на грека походил мало. Скорее на пройдоху-купца из финикийцев. Ишь, притащился с утра пораньше.
– Слышь, Фалес, или как там тебя. Я тебе зла не желаю, но шёл бы ты отсюда подобру-поздорову. Жрецы и так смеются – мол, никогда не видали они мудрых греков. Греки – славные воины, не дураки выпить, но где им
состязаться в мудрости с потомственными жрецами чуть не в 20-м поколении. И раз жрецы не могут, не измеряя саму пирамиду, определить её высоту, то и пришлому греку не стоит хвастаться. Ну, это они так говорят,
но я с ними согласен. Так что смотри – касаться священных камней пирамиды ни тебе, ни твоему рабу не позволено. И я не могу разрешить тебе нарушить запрет. Садитесь лучше на корабль и плывите себе. Я уж всё
объясню Амасису.
– Спасибо, дружище. Но я всё же попробую – ответил Фалес. Он отошёл от начальника стражи и направился в сторону тени, падающей от пирамиды. Шёл он, опираясь на высокий, в полтора человеческих роста
остроконечный посох, а пожилой раб шагал рядом с приличного размера мешком, хотя и не похоже, что тяжёлым. Подойдя к вершине тени, он воткнул точно в вершину посох и укрепил его вертикально, пользуясь при
этом отвесом. В это же время раб забил колышек в то место, куда попала вершина тени посоха. Затем Фалес вытащил из мешка длинную верёвку с равномерно завязанными на ней узелками. И привязал её одним
концом к закреплённому основанию посоха.
Солнце между тем продолжало подниматься. Близился полдень. Прибыли в крытых повозках жрецы. Прибыл и фараон Амасис, по старой привычке предпочитая боевую колесницу паланкину. Все расположились у
подножья пирамиды, в тени, оживлённо переговариваясь и смеясь. Пусть грек начинает свои фокусы – сказал Амасис начальнику стражи. А то на обед опоздаем.
Фалес, оставаясь у посоха, кивнул рабу, и тот, насколько мог быстро, заковылял к переместившейся вершине тени от пирамиды, разматывая за собой верёвку. Добежав до цели, от натянул верёвку, завязал на ней ещё
один заметный узел, затем ослабил её и прокричал, что всё готово. В тот же момент Фалес, до того крепко удерживавший посох, чтобы тот не шевелился, воткнул второй колышек в то место, куда показывала тень посоха. Пока раб возвращался, Фалес измерил расстояние между колышками и длину возвышающейся части посоха. Затем они вместе с рабом пересчитали узелки на верёвке – чтоб не ошибиться. Всё записывали тут же, на песке, затем что-то делили, умножали. Раб бормотал тихонько: “Ну и остолоп же ты. Сколько тебя учу, а всё ошибаешься в счёте”. И вот Фалес выпрямился, поклонился Амасису, жрецам и объявил высоту прирамиды – 280 царских локтей. Амасис вопросительно посмотрел на жрецов, они утвердительно закивали.
Ну, ни хрена себе, подумал Амасис. Начиналась эпоха греческих научных и культурных достижений. Древнегреческих, конечно.
Схема измерений прилагается.

Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.

Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.

Чтобы сообразить это, Фалес должен был уже много знать про геометрические фигуры, а особенно про ту, которая получается, если разбить квадрат на два треугольника. А дальше, вероятно, Фалес рассуждал так.

Солнце от Земли очень далеко, поэтому идущие от него и к пирамиде лучи можно без большой ошибки считать параллельными. Но когда тень от палки станет той же длины, что и сама палка, то треугольник АВС станет прямоугольным и равнобедренным. А из параллельности солнечных лучей он вывел, что тогда и треугольник DEC на том же рисунке тоже станет равнобедренным, а значит, высота пирамиды будет равна длине её тени.

Самый легкий и самый древний способ — без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего по тени высоту огромного сооружения.

Фалес, — говорит предание, — избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени (‘). Вот, пожалуй, единственный случай, когда человек извлекает пользу из своей тени.

Задача греческого мудреца представляется нам теперь детски-простой, но не будем забывать, что смотрим мы на нее с высоты геометрического здания, воздвигнутого уже после Фалеса. Он жил задолго до Евклида, автора замечательной книги, по которой обучались геометрии в течение двух тысячелетий после его смерти. Заключенные в ней истины, известные теперь каждому школьнику, не были еще открыты в эпоху Фалеса. А чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес сам открыл):

1) что углы при основании равнобедренного треугольника равны, и обратно—что стороны, лежащие против равных углов треугольника, равны между собою;

2) что сумма углов всякого треугольника (или по крайней мере прямоугольного) равна двум прямым углам.

Только вооруженный этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды, середина ее основания и конец ее тени должны обозначить равнобедренный треугольник. Этим простым способом очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних.

Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда.

Рис.1 Измерение высоты дерева по тени.

Нетрудно, однако, изменить этот способ так, чтобы в солнечный день можно было пользоваться любой тенью, какой бы длины она ни была. Измерив, кроме того, и свою тень или тень какого-нибудь шеста, вычисляют искомую высоту из пропорции (рис. 1):

т. е. высота дерева во столько же раз больше вашей собственной высоты (или высоты шеста), во сколько раз тень дерева длиннее вашей тени (или тени шеста). Это вытекает, конечно, из геометрического подобия треугольников ABC и аbc (по двум углам).

к теням, отбрасываемым при свете уличного фонаря или лампы,— оно не оправдается. На рис. 2 вы видите, что столбик АВ выше тумбы ab примерно втрое, а тень столбика больше тени тумбы (ВС:bс) раз в восемь. Объяснить, почему в данном случае способ применим, а в другом нет, — невозможно

Рис.2 Когда такое измерение не выполнимо.

Рассмотрим поближе, в чем тут разница. Суть дела сводится к тому, что солнечные лучи между собою параллельны, лучи же фонаря — непараллельны. Последнее очевидно; но почему вправе мы считать лучи Солнца параллельными, хотя они безусловно пересекаются в том месте, откуда исходят?

Лучи Солнца, падающие на Землю, мы можем считать параллельными потому, что угол между ними чрезвычайно мал, практически неуловим. Несложный геометрический расчет убедит вас в этом. Вообразите два луча, исходящие из какой-нибудь точки Солнца и падающие на Землю в расстоянии, скажем, одного километра друг от друга. Значит, если бы мы поставили одну ножку циркуля в эту точку Солнца, а другою описали окружность радиусом, равным расстоянию от Солнца до Земли (т. е. радиусом в 150 000 000 км) то между нашими двумя лучами-радиусами оказалась бы дуга в один километр длиною. Полная длина этой исполинской окружности была бы равна 2π× 150 000 000км = 940 000 000 км. Один градус ее, конечно, в 360 раз меньше, т. е. около 2 600 000 км; одна дуговая минута в 60 раз меньше градуса, т. е. равна 43000 км, а одна дуговая секунда еще в 60 раз меньше,

т. е. 720 км. Но наша дуга имеет в длину всего только 1 км; значит, она соответствует углу в секунды. Такой ничтожный угол неуловим даже для точнейших астрономических инструментов; следовательно, на практике мы можем считать лучи Солнца, падающие на Землю, за параллельные прямые. Если бы эти геометрические соображения не были нам известны, мы не могли бы обосновать рассматриваемый способ определения высоты по тени. Пробуя применить способ теней на практике, вы сразу же убедитесь, однако, в его ненадёжности. Тени не отграничены так отчетливо, чтобы измерение их длины можно было выполнить вполне точно. Каждая тень, отбрасываемая при свете Солнца, имеет неясно очерченную серую кайму полутени, которая и придает границе тени неопределенность. Происходит это оттого, что Солнце — не точка, а большое светящееся тело, испускающее лучи из многих точек. На рис. 3 показано, почему вследствие этого тень ВС дерева имеет еще придаток в виде полутени CD, постепенно сходящей на-нет.

Рис. 3 Как образуется полутень.

Угол CAD между крайними границами полутени равен тому углу, под которыми мы всегда видим солнечный диск, т. е. половине градуса. Ошибка, происходящая от того, что обе тени измеряются не вполне точно, может при неслишком даже низком стоянии Солнца достигать 5% и более. Эта ошибка прибавляется к другим неизбежным ошибкам — от неровности почвы и т.д.—и делает окончательный результат мало надежным. В местности гористой, например, способ этот совершенно неприменим.

Еще два способа

Вполне возможно обойтись при измерении высоты и без помощи теней. Таких способов много; начнем с двух простейших. Прежде всего мы можем воспользоваться свойством равнобедренного прямоугольного треугольника, обратившись к услугам весьма простого прибора, который весьма легко изготовить из дощечки и трех булавок. На дощечке любой формы, даже на куске коры, если у него есть плоская сторона, намечают три точки — вершины равнобедренного прямоугольного треугольника— и в них втыкают торчком по булавке (рис. 4).

Рис.4 Булавочный прибор для измерения высот.

Пусть у вас нет под рукой чертежного треугольника для построения прямого угла, нет и циркуля для отложения равных сторон. Перегните тогда любой лоскут бумаги один раз, а затем поперек первого сгиба еще раз так, чтобы обе части первого сгиба совпали, — и получите прямой угол. Та же бумажка пригодится и вместо циркуля, чтобы отмерить равные расстояния.

Как видите, прибор может быть целиком изготовлен в бивуачной обстановке.

Обращение с ним не сложнее изготовления. Отойдя от измеряемого дерева, держите прибор так, чтобы один из катетов треугольника был направлен отвесно, для чего можете пользоваться ниточкой с грузиком, привязанной к верхней булавке.

Рис.5 Схема применения булавочного прибора.

Приближаясь к дереву или удаляясь от него, вы всегда найдете такое место А (рис. 5), из которого, глядя на булавки a и c, увидите, что они покрывают верхушку С дерева: это значит, что продолжение гипотенузы ас проходит через точку С. Тогда, очевидно, расстояние аВ равно СВ, так как угол α = 45°. Следовательно, измерив расстояние аВ (или, на ровном месте, одинаковое с ним расстояние AD) и прибавив BD, т. е. возвышение аА глаза над землей, получите искомую высоту дерева.

По другому способу вы обходитесь даже и без булавочного прибора. Здесь нужен шест, который вам придется воткнуть отвесно в землю так, чтобы выступающая часть как раз равнялась вашему росту. Место для шеста надо выбрать так, чтобы, лежа, как показано на рис. 6, вы видели верхушку дерева на одной прямой линии с верхней точкой шеста. Так как треугольник Abc— равнобедренный и прямоугольный, то угол А = 45° и, следовательно, АВ равно ВС, т. е. искомой высоте дерева.

Рис.6 Ещё один способ измерения высоты дерева.

Как поступил сержант

Некоторые из только что описанных способов измерения высоты неудобны тем, что вызывают необходимость ложиться на землю. Можно, разумеется, избежать такого неудобства. Вот как однажды было на одном из фронтов Великой Отечественной войны. Подразделению лейтенанта Иванюк было приказано построить мост через горную реку. На противоположном берегу засели фашисты. Для разведки места постройки моста лейтенант выделил разведывательную группу во главе со старшим сержантом Поповым . В ближайшем лесном массиве они измерили диаметр и высоту наиболее типичных деревьев и подсчитали количество деревьев,

Рис.8 Измерение высоты дерева при помощи шеста.

которые можно было использовать для постройки. Высоту деревьев определяли при помощи вешки (шеста) так, как показано на рис. 8.

Этот способ состоит в следующем. Запасшись шестом выше своего роста, воткните его в землю отвесно на некотором расстоянии от измеряемого дерева (рис. 8). Отойдите от шеста назад, по продолжению Dd до того места А, с которого, глядя на вершину дерева, вы увидите на одной линии с ней верхнюю точку b шеста. Затем, не меняя положения головы, смотрите по направлению горизонтальной прямой аС, замечая точки с и С, в которых луч зрения встречает шест и ствол. Попросите помощника сделать в этих местах пометки, и наблюдение окончено. Остается только на основании подобия треугольников abc и аВС вычислить ВС из пропорции ВС:bc=aC:ac

откуда ВС=Ьс·

Расстояния bс, аС и ас легко измерить непосредственно. К полученной величине ВС нужно прибавить расстояние CD (которое также измеряется непосредственно), чтобы узнать искомую высоту дерева.

Для определения количества деревьев старший сержант приказал солдатам измерить площадь лесного массива. Затем он подсчитал количество деревьев на небольшом участке размером 50X50 кв. м и произвел соответствующее умножение.

На основании всех данных, собранных разведчиками, командир подразделения установил, где и какой мост нужно строить. Мост построили к сроку, боевое задание было выполнено успешно.

Читайте также:

  

• Почему сша активно содействовали их проведению кратко

  

• Нормативно правовое обеспечение деятельности доу в годовом плане

  

• Почему нельзя пить морскую воду при жажде кратко

  

• Как изменяются имена прилагательные кратко

  

• Почему люди так часто травмируются кратко

Categories:

• Наука
• История
• Cancel

Фалес (Талес) и пирамида

Когда вспоминают об основоположнике греческой науки и философии – Фалесе Милетском, обязательно, наряду с теоремой Фалеса об отрезках, отсекаемых параллельными на сторонах угла, вспоминают и остроумный способ определения высоты пирамиды Хеопса. Разные авторы пишут разное, но все сходятся в том, что он проводил одно измерение длины тени пирамиды и одно – тени шеста или тени своего тела. Почему-то при этом считается, что длину тени пирамиды легко измерить. А ведь это по условиям легенды невозможно. Как добраться до проекции вершины на плоскость основания, не производя никаких измерений самой пирамиды?

Я предлагаю некий фантастический рассказ о том, как же всё это происходило. На историческую достоверность, разумеется, не претендую.

С утра у великой пирамиды Хуфу выстроилась стража. В полдень ожидали Амасиса и жрецов. Начальник стражи, поседевший в битвах грек-наёмник, сражавшийся под водительством фараона тогда, когда тот ещё и
фараоном не был, недовольно разглядывал своего соотечественника. Впрочем, тот и на грека походил мало. Скорее на пройдоху-купца из финикийцев. Ишь, притащился с утра пораньше.
– Слышь, Фалес, или как там тебя. Я тебе зла не желаю, но шёл бы ты отсюда подобру-поздорову. Жрецы и так смеются – мол, никогда не видали они мудрых греков. Греки – славные воины, не дураки выпить, но где им
состязаться в мудрости с потомственными жрецами чуть не в 20-м поколении. И раз жрецы не могут, не измеряя саму пирамиду, определить её высоту, то и пришлому греку не стоит хвастаться. Ну, это они так говорят,
но я с ними согласен. Так что смотри – касаться священных камней пирамиды ни тебе, ни твоему рабу не позволено. И я не могу разрешить тебе нарушить запрет. Садитесь лучше на корабль и плывите себе. Я уж всё
объясню Амасису.
– Спасибо, дружище. Но я всё же попробую – ответил Фалес. Он отошёл от начальника стражи и направился в сторону тени, падающей от пирамиды. Шёл он, опираясь на высокий, в полтора человеческих роста
остроконечный посох, а пожилой раб шагал рядом с приличного размера мешком, хотя и не похоже, что тяжёлым. Подойдя к вершине тени, он воткнул точно в вершину посох и укрепил его вертикально, пользуясь при
этом отвесом. В это же время раб забил колышек в то место, куда попала вершина тени посоха. Затем Фалес вытащил из мешка длинную верёвку с равномерно завязанными на ней узелками. И привязал её одним
концом к закреплённому основанию посоха.
Солнце между тем продолжало подниматься. Близился полдень. Прибыли в крытых повозках жрецы. Прибыл и фараон Амасис, по старой привычке предпочитая боевую колесницу паланкину. Все расположились у
подножья пирамиды, в тени, оживлённо переговариваясь и смеясь. Пусть грек начинает свои фокусы – сказал Амасис начальнику стражи. А то на обед опоздаем.
Фалес, оставаясь у посоха, кивнул рабу, и тот, насколько мог быстро, заковылял к переместившейся вершине тени от пирамиды, разматывая за собой верёвку. Добежав до цели, от натянул верёвку, завязал на ней ещё
один заметный узел, затем ослабил её и прокричал, что всё готово. В тот же момент Фалес, до того крепко удерживавший посох, чтобы тот не шевелился, воткнул второй колышек в то место, куда показывала тень посоха. Пока раб возвращался, Фалес измерил расстояние между колышками и длину возвышающейся части посоха. Затем они вместе с рабом пересчитали узелки на верёвке – чтоб не ошибиться. Всё записывали тут же, на песке, затем что-то делили, умножали. Раб бормотал тихонько: “Ну и остолоп же ты. Сколько тебя учу, а всё ошибаешься в счёте”. И вот Фалес выпрямился, поклонился Амасису, жрецам и объявил высоту прирамиды – 280 царских локтей. Амасис вопросительно посмотрел на жрецов, они утвердительно закивали.
Ну, ни хрена себе, подумал Амасис. Начиналась эпоха греческих научных и культурных достижений. Древнегреческих, конечно.
Схема измерений прилагается.

Во всех исследованиях и источниках по истории античной математики Фалес Милетский (625-547 до Р.Х.) упоминается как первый древнегреческий математик и философ. Относительно геометрических открытий Фалеса все источники единодушны. Думается, что более простой признак равенства треугольников, по двум сторонам и углу между ними, Фалесу тоже был известен. Известно также, что Фалес посещал Египет, где определил высоту одной из пирамид. Утверждается, кроме того, что Фалес обучался геометрии у египетских жрецов, что, на наш взгляд, весьма сомнительно (точнее сказать, следует полностью отвергнуть такую возможность, подробнее об этом будет сказано далее).
Автор великолепного исследования известный математик Б.Л. Ван дер Варден выдвигает свою версию творчества Фалеса, с которой, к сожалению, согласиться не представляется возможным. По Б.Л. Ван дер Вардену получается, что Фалес в деталях ознакомился не только с египетскими, но и с вавилонскими математическими знаниями. Его не устраивало, что эти знания состоят, по существу, из нагромождения необоснованных фактов, а также отдельные факты противоречат друг. Фалес решил во всем этом разобраться и стал строить геометрию в виде дедуктивной системы, двигаясь от простых фактов к сложным. На наш взгляд, эта гипотеза весьма уязвима. Выходит, что Фалес, взявшись за дедуктивное построение геометрии, бросил это занятие, едва получив самые простые факты (заметим, Фалес прожил 80 лет и времени у него было достаточно). Не понятно, в связи с этим, в чем причина огромной популярности Фалеса у образованной античной публики.

Позволим себе высказать некоторые соображения на этот счет. Популярность Фалесу снискали не открытые им факты, касающиеся треугольников и кругов, а проведенные им эффектные определения длин и расстояний, не доступных непосредственному измерению. Как уже отмечалось выше, Фалес определил высоту одной из египетских пирамид. Кроме этого, он определял расстояние до корабля в море, возможно, какие-то другие величины, например, ширину реки. Открытые Фалесом геометрические факты составляют необходимый набор для решения этих задач.
Начнем с рассмотрения наиболее сложной задачи из этого перечня: задачи определения высоты пирамиды. Заметим, то, что Фалес взялся за это предприятие, говорит о том, что он не имел непосредственного общения с жрецами (по крайней мере, доверительного). Трудно представить, что жрецы не знали какова высота этой пирамиды. Маловероятно также, что они поставили Фалесу эту задачу в качестве теста на сообразительность.
Приведем цитату из, которая воспринимается как курьез. Речь идет о методе, которым Фалес измерил высоту пирамиды: «Этот метод до удивления прост. Вначале Фалес с помощью обычной палки установил час, когда тень и высота тела равны между собой, а затем в тот же час он измерил тень пирамиды, которая и была ее высотой». На самом деле не все так просто, как кажется авторам. Пирамида — не палка и имеет массивное квадратное основание. А для того, чтобы непосредственно измерить длину тени, надо добраться до центра этого квадрата (что сделать не возможно). Фалес мог только отметить точку, куда падает тень от вершины пирамиды. Заметим, что необходимым условием существования такой точки является то, чтобы высота пирамиды была бы больше половины стороны основания (иначе в назначенный час вся боковая поверхность пирамиды будет освещена). Самая высокая из пирамид этому условию удовлетворяет. Когда точка, в которую попадает тень вершины (пусть это — точка А), найдена, то высота пирамиды может быть найдена в результате выполнения следующей процедуры. Найдем точку В — ближайшую к А из середин сторон основания, затем найдем точку С так, чтобы ВС было перпендикулярно к этой стороне и АС было перпендикулярно ВС. Фалес мог это сделать, опираясь на известные ему геометрические факты. Восставить из точки. В перпендикуляр к стороне пирамиды можно используя свойства равнобедренных треугольников.
Выберем на стороне пирамиды по разные стороны от В две точки Bt и В2, так, чтобы BBj=BB2. Возьмем веревку длиной раза в три (приблизительно) больше длины BjB2. Перегнув веревку пополам, зафиксируем ее середину. Закрепим концы веревки в точках Bj и В 2 и натянем ее за середину до упора. Середина веревки ляжет в некоторую точку Cj, при этом BCj будет перпендикулярно стороне пирамиды (на которой лежит точка В). Теперь на продолжении отрезка BCt надо найти точку С, о которой сказано выше. Это можно сделать следующим образом. Найдем точку At — середину АВ и проведем окружность с центром в Aj радиуса А1В. Пересечение этой окружности с продолжением BCt и есть точка С. Обозначим О — недоступную нам точку — центр основания пирамиды. Тогда искомая длина тени, она же высота пирамиды, это — длина отрезка OA, который является гипотенузой прямоугольного треугольника ОАС. Катет АС доступен, его длину можно измерить непосредственно. Длина же катета ОС равна сумме длины отрезка СВ и половины длины стороны основания пирамиды. Итак, по известным катетам надо определить гипотенузу. Теорему Пифагора Фалес не знал (иначе эта теорема называлась бы теоремой Фалеса). Видимо, он просто воспроизвел на свободной площадке копию треугольника ОАС.

Сформулируем свою точку зрения на математическое творчество Фалеса. Фалес располагал ограниченным набором элементарных (по сравнению с полученными позднее другими греческими учеными) геометрических фактов. При этом основной задачей Фалеса было определение длин, недоступных непосредственному измерению. Факты (теоремы) он обосновывал с помощью аргументации, которую можно отнести к разряду мысленных экспериментов. Например, он «доказывал» равенство углов при основании равнобедренного треугольника примерно так: если разрезать треугольник по биссектрисе угла при вершине , то получим два равных треугольника. Фалес был вынужден при-
бегать к теоретическим обоснованиям, так как, имея дело с недоступными расстояниями, он не мог проверить свои утверждения опытным путем. Далее, Фалес не придавал совокупности геометрических фактов статус отдельной научной дисциплины (выражаясь современным языком). Заметим в связи с этим, что его ученик Анаксимандр и ученик Анаксимандра Анаксимен вопросов геометрии не касались. Хотя аргументация Фалеса не может рассматриваться в качестве полноценного доказательства теорем, как у Евклида, но, безусловно, дедуктивное построение геометрии начинается именно с него.