Как геометрически найти корень - Сайт, где вы сможете решить свои вопросы

Методы вычисления квадратных корней — это вычислительные алгоритмы для вычисления приближённых значений главных (или неотрицательных) квадратных корней (обычно обозначаемых как , или ${displaystyle S^{1/2}}$ ) вещественного числа. Арифметически это означает, что если дано число , процедура находит число, которое при умножении на себя даёт . Алгебраически это означает процедуру нахождения неотрицательного корня уравнения ${displaystyle x^{2}-S=0}$ . Геометрически это означает построение стороны квадрата с заданной площадью.

Любое вещественное число имеет два корня^[1]. Главное значение квадратного корня большинства чисел является иррациональным числом с бесконечной последовательностью десятичных цифр. Как результат, десятичное представление любого такого квадратного корня может быть вычислено только приближённо с конечной точностью (знаков после запятой). Однако, даже если мы берём корень от полного квадрата целого числа, так что результат имеет конечное представление, некоторые процедуры, используемые для вычисления корня, могут вернуть лишь ряд приближений с возрастающей точностью.

Представление вещественного числа в виде цепной дроби может быть использовано вместо десятичного или двоичного разложения и это представление имеет свойство, что квадратный корень любого рационального числа (который не является полным квадратом) имеет период, то есть периодическое разложение, похожее на то, как рациональные числа имеют повторяющееся разложения десятичной системе счисления.

Большинство общепризнанных аналитических методов являются итеративными и состоят из двух шагов: нахождения подходящего начального значения с последующим итеративным уточнением пока не будет достигнут определённый критерий остановки. Начальным значением может быть любое число, но если оно ближе к конечному значению, число требуемых итераций потребуется меньше. Наиболее известным таким методом, да ещё и удобным для программирования, является метод Ньютона, который основывается на вычислении производной. Несколько методов, такие как обычное деление вручную по схеме Горнера или разложение в ряд, не требуют задание начального значения. В некоторых приложениях требуется найти целочисленный квадратный корень, который является квадратным корнем, округлённым до ближайшего целого (в этом случае может быть использована модифицированная процедура).

Используемый метод зависит от того, как результат будет использован (то есть, насколько точен должен быть результат) и какие средства есть под рукой. Методы можно грубо разбить на те, которые можно выполнить в уме, которые требуют карандаша и листа бумаги, или те, которые реализуются в виде программы и выполняются на компьютерах или других вычислительных устройствах. Могут приниматься в расчёт скорость сходимости (сколько итераций потребуется для достижения заданной точности), вычислительной сложности отдельных операций (таких как деление) или итераций, и распределение ошибок (точность результата).

Процедуры поиска квадратных корней (в частности, корня из 2) известны по меньшей мере со времён древнего Вавилона (17-й век до нашей эры). Метод Герона из Египта первого века был первым проверяемым алгоритмом для вычисления квадратного корня. Современные аналитические методы начались разрабатываться после принятия арабских цифр в Западной Европе в Раннем Ренессансе. В настоящие дни почти все вычислительные устройства имеют функцию быстрого и точного вычисления квадратного корня в виде встроенной конструкции языка программирования, библиотечной функции или аппаратного оператора, которые основываются на описанных ниже процедурах.

Начальная оценка[править | править код]

Многие итеративные алгоритмы вычисления квадратного корня требуют задания начального случайного значения. Это значение должно быть ненулевым положительным числом. Оно должно быть между 1 и , числом, квадратным корень которого мы ищем, поскольку квадратный корень должен быть в этих пределах. Если начальное значение очень далеко от корня, алгоритму потребуется больше итераций. Если начать с ${displaystyle x_{0}=1}$ (или с ), будет отработано лишних примерно ${displaystyle {tfrac {1}{2}}vert log _{2}Svert }$ итераций просто для получения порядка корня. Поэтому полезно иметь грубую оценку корня, которая может иметь слабую точность, но зато легко вычисляется. В общем случае чем точнее оценка, тем быстрее сходимость. Для метода Ньютона (называемого также вавилонским или методом Герона), начальное значение несколько большее корня даёт более быструю сходимость, по сравнению с начальным значением, меньшим корня.

Вообще говоря, оценка рассматривается на произвольном интервале, в котором известно, что в нём содержится корень (таком как ${displaystyle [x_{0},S/x_{0}]}$ ). Получение лучшей оценки вовлекает либо получение более узких границ интервала, либо лучшего функционального приближения к Последнее обычно означает использование для аппроксимации многочленов более высокого порядка, хотя не все аппроксимации используют многочлены. Общие методы оценки бывают скалярные, линейные, гиперболические и логарифмические. Десятичная система счисления обычно используется для оценки в уме или на бумаге. Двоичная система счисления более пригодна для компьютерных оценок. При оценке экспонента и мантисса обычно обрабатываются отдельно.

Десятичная оценка[править | править код]

Обычно число выражается в экспоненциальном виде как ${displaystyle atimes 10^{2n}}$ , где , а n — целое число, тогда оценкой возможного квадратного корня может быть ${displaystyle {sqrt {a}}times 10^{n}}$ , где .

Скалярные оценки[править | править код]

Скалярные методы делят весь диапазон на интервалы и оценка в каждом интервале представлена одним числом. Если диапазон рассматривается как один интервал, то арифметическое среднее (5,5) или геометрическое среднее ( ${displaystyle {sqrt {10}}approx 3{,}16)times 10^{n}}$ являются приемлемыми оценками. Абсолютная и относительная оценка для этих оценок будет отличаться. В общем случае отдельное число будет очень неточно. Более точные оценки разбивают диапазон на два и более интервалов, но скалярная оценка продолжает оставаться очень грубой.

Для двух интервалов, разбитых геометрически, квадратный корень ${displaystyle {sqrt {S}}={sqrt {a}}times 10^{n}}$ можно оценить как^[2].

${displaystyle {sqrt {S}}approx {begin{cases}2cdot 10^{n}&{text{если }}a<10,\6cdot 10^{n}&{text{если }}ageqslant 10.end{cases}}}$

Эта оценка имеет максимальную абсолютную погрешность ${displaystyle 4cdot 10^{n}}$ в точке = 100 и максимальную относительную ошибку в 100% в точке = 1.

Например, для с разложением ${displaystyle 12{,}5348times 10^{4}}$ , оценка будет ${displaystyle {sqrt {S}}approx 6cdot 10^{2}=600}$ . , с абсолютной ошибкой 246 и относительной ошибкой почти 70%.

Линейная оценка[править | править код]

Лучшей оценкой и стандартным методом является линейное приближение функции y = x^2 на малой дуге. Если, как и выше, степень выделена из числа , а интервал сокращён до , можно использовать секущую или касательную где-то вдоль дуги для аппроксимации, но прямая регрессии метода наименьших квадратов будет более точной.

Прямая, получающаяся методом наименьших квадратов, минимизирует среднее расстояние между оценкой и значением функции. Её уравнение — . После преобразования и округления коэффициентов для упрощения вычислений получим

${displaystyle {sqrt {S}}approx (a/10+1{,}2)cdot 10^{n}}$

Это лучшая оценка в среднем, которую можно получить одной попыткой линейной аппроксимации функции y=x^2 в интервале . Оценка имеет максимальную абсолютную ошибку 1,2 в точке a=100 и максимальную относительную ошибку в 30% в точках S=1 и 10^[3].

Чтобы разделить на 10, вычитаем единицу из показателя степени или, образно говоря, передвигаем десятичную запятую на одну позицию влево. Для этой формулы любая добавленная константа, равная 1 плюс маленькое приращение, даёт удовлетворительную оценку, так что запоминать точное число нет необходимости. Аппроксимация (округлённая или не округлённая) с помощью одной прямой, стягивающей область по точности даёт не более одного верного знака. Относительная ошибка более чем 1/2², так что даёт менее 2 битов информации. Точность сильно ограничена, поскольку область охватывает два порядка, что достаточно большая величина для такого рода оценок.

Существенно лучшую оценку можно получить при помощи кусочно–линейной аппроксимации, то есть с помощью нескольких отрезков, которые приближают поддугу исходной дуги. Чем больше отрезков используется, тем лучше приближение. Наиболее употребительно применение касательных. Критичным моментом является как делить дугу и где располагать точки касания. Действенным методом деления дуги от y=1 до y=100 является геометрический — для двух интервалов границей интервалов является квадратный корень исходного интервала, 1*100, то есть и . Для трёх интервалов будут кубические корни — ${displaystyle [1,{sqrt[{3}]{100}}],[{sqrt[{3}]{100}},({sqrt[{3}]{100}})^{2}]}$ , и ${displaystyle [({sqrt[{3}]{100}})^{2},100]}$ , и так далее. Для двух интервалов является очень удобным числом. Легко получить касательные прямые в точках касания и . Их уравнения: и . Обращая уравнения, получим, что квадратные корни равны и . Тогда для ${displaystyle S=acdot 10^{2n}}$ :

${displaystyle {sqrt {S}}approx {begin{cases}(0{,}28a+0{,}89)cdot 10^{n}&{text{если }}a<10,\(0{,}089a+2{,}8)cdot 10^{n}&{text{если }}ageqslant 10.end{cases}}}$

Максимальные абсолютные значения оказываются в правых границах интервалов, в точках a=10 и 100, и равны 0,54 и 1,7 соответственно. Максимальные относительные ошибки появляются на концах интервалов, в точках a=1, 10 и 100, и равны 17%. 17% или 0,17. Они больше, чем 1/10, так что метод даёт точность менее одной значащей цифры.

Гиперболическая оценка[править | править код]

В некоторых случаях может оказаться действенной гиперболическая оценка, поскольку гипербола также является выпуклой кривой и может лежать вдоль дуги Y = x² лучше, чем прямая. Гиперболическая оценка вычислительно более сложная, поскольку для неё нужно деление на число с плавающей запятой. Почти оптимальной гиперболической аппроксимацией к x² на интервале является . После преобразования получим . Тогда для ${displaystyle S=acdot 10^{2n}}$ :

${displaystyle {sqrt {S}}approx left({frac {-190}{a+20}}+10right)cdot 10^{n}}$

Деление с плавающей запятой должно быть с точностью до одного десятичного знака, поскольку вся оценка даёт такую точность, и такое деление можно выполнить в уме. Гиперболическая оценка в среднем лучше, чем скалярная или линейная оценка. Её максимальная абсолютная ошибка составляет 1,58 в точке 100, а максимальная относительная ошибка составляет 16,0% в точке 10. Для худшего случая a=10 оценка равна 3,67. Если начать с 10 и применять итерации Нютона-Рапсона напрямую, требуется две итерации, которые дают 3,66, прежде чем достичь точности гиперболической оценки. Для более типичного случая наподобие 75 гиперболическая оценка даёт 8,00 и требуется 5 итераций Ньютона-Рапсона с начальным значением 75, чтобы получить более точный результат.

Арифметическая оценка[править | править код]

Метод, аналогичный кусочно-линейной аппроксимации, но использующий лишь арифметические операции вместо алгебраических уравнений, использует таблицу умножения в обратную сторону — квадратный корень чисел между 1 и 100 где-то между 1 и 10, так что, поскольку мы знаем, что 25 является точным квадратом (5 × 5) и 36 является точным квадратом (6 × 6), то квадратный корень из числа, которое больше 25, но меньше 36, начинается с цифры 5. Аналогично для чисел между другими квадратами. Этот метод даёт правильный первый знак, но точность его всего одна цифра — первая цифра квадратного корня из 35, например, равна 5, но сам корень из 35 почти равен 6.

Лучше делить интервал между двумя квадратами пополам. Так что корень любого числа между 25 и половины пути до 36 (что есть 30,5) оценивается как 5, остальные числа, большие 30,5 вплоть до 36 оцениваются как 6^[4]. Процедура требует очень мало арифметики для нахождения середины двух произведений из таблицы. Вот таблица таких чисел:

a	nearest square	est.
1 to 2,5	1 (= 1²)	1
2,5 to 6,5	4 (= 2²)	2
6,5 to 12,5	9 (= 3²)	3
12,5 to 20,5	16 (= 4²)	4
20,5 to 30,5	25 (= 5²)	5
30,5 to 42,5	36 (= 6²)	6
42,5 to 56,5	49 (= 7²)	7
56,5 to 72,5	64 (= 8²)	8
72,5 to 90,5	81 (= 9²)	9
90,5 to 100	100 (= 10²)	10

Конечной операцией будет умножение оценки k на степень десятки, делённой пополам, так что для ${displaystyle S=acdot 10^{2n}}$ ,

${displaystyle {sqrt {S}}approx kcdot 10^{n}}$

Метод даёт точность в одну значащую цифру, поскольку он округляет до лучшей первой цифры.

Метод можно распространить до 3 значащих цифр в большинстве случаев, интерполируя между ближайшими квадратами. Если ${displaystyle k^{2}leqslant a<(k+1)^{2}}$ , то примерно равен k плюс дробь, равная разности a и $k^{2}$ , делённой на разность между двумя квадратами:

где ${displaystyle R={frac {(a-k^{2})}{(k+1)^{2}-k^{2}}}}$

Конечной операцией, как и выше, служит умножение результата на степень десятки, делённой пополам

${displaystyle {sqrt {S}}={sqrt {a}}cdot 10^{n}approx (k+R)cdot 10^{n}}$

Число k есть десятичная цифра, а R есть дробь, которую следует превратить в десятичную. Дробь имеет обычно одну цифру в числителе и одну или две цифры в знаменателе, так что преобразование в десятичную дробь можно провести в уме.

Пример: найти квадратный корень из 75. ${displaystyle 75=75times 10^{2cdot 0}}$ , так что a равно 75, а n равно 0. Исходя из таблицы умножения квадратный корень мантиссы должен быть 8 с дробью, поскольку , а , слишком велико. Так что k равно 8 с дробью является десятичным представлением R. Дробь R имеет ${displaystyle 75-k^{2}=11}$ в числителе и ${displaystyle 81-k^{2}=17}$ в знаменателе. 11/17 чуть меньше, чем 12/18, что равно 2/3 или 0,67, так что 0,66 является хорошим предположением (здесь можно ограничиться и предположением поскольку ошибка мала). Так что оценка корня равна . √75 до трёх значащих цифр будет 8,66, так что оценка до трёх значащих цифр хорошая. Не все оценки с помощью такого метода столь точны, но они довольно близки.

Двоичная оценка[править | править код]

Когда работа ведётся в двоичной системе счисления (скажем, в процессоре компьютера), выражается как ${displaystyle atimes 2^{2n}}$ , где ${displaystyle 0{,}1_{2}leqslant a<10_{2}}$ , квадратный корень ${displaystyle {sqrt {S}}={sqrt {a}}times 2^{n}}$ можно оценить величиной

${displaystyle {sqrt {S}}approx (0{,}485+0{,}485cdot a)cdot 2^{n}}$

что является регрессией методом наименьших квадратов по 3 старшим битам. имеет максимальную абсолютную ошибку 0,0408 в точке =2 и максимальную относительную ошибку в 3,0% в точке =1. Для вычислений удобна округлённая оценка (поскольку коэффициенты являются степенями 2)

${displaystyle {sqrt {S}}approx (0{,}5+0{,}5cdot a)cdot 2^{n}}$

^[5]

которая имеет максимальную абсолютную ошибку 0,086 в точке 2 и максимальную относительную ошибку в 6,1% в точках и .

Для ${displaystyle S=125348=1;1110;1001;1010;0100_{2}=1{,}1110;1001;1010;0100_{2}times 2^{16},}$ двоичное приближение даёт ${displaystyle {sqrt {S}}approx (0{,}5+0{,}5cdot a)cdot 2^{8}=1{,}0111;0100;1101;0010_{2}cdot 1;0000;0000_{2}=1{,}456cdot 256=372{,}8.}$ Поскольку , оценка даёт абсолютную ошибку в 19 и относительную ошибку 5,3%. Относительная ошибка чуть меньше 1/2⁴, так что приближение даёт точность до 4+ бит.

Оценку для с точностью до 8 бит можно получить путём просмотра таблицы по старшим 8 битам , учитывая, что старший бит задаётся неявно в большинстве представлений чисел с плавающей запятой, а младшие биты после 8 бит должны быть округлены. Таблица содержит 256 байт заранее вычисленных 8-битных квадратных корней. Например, для индекса 11101101₂, что в десятичной системе равно 1,8515625₁₀, значение в таблице равно 10101110₂, что в десятичной системе равно 1,359375₁₀, квадратному корню числа 1,8515625₁₀ с точностью до 8 бит (2+ десятичных знака).

Вавилонский метод[править | править код]

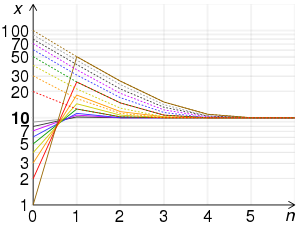
Полулогарифмические графики сравнения скорости сходимости вавилонского метода нахождения квадратного корня для 100 различных начальных значений. Отрицательное начальное значение приводит к отрицательному корню. Заметим, что более близкие к корню значения сходятся быстрее, и все приближения являются завышенными. В SVG файле наведите курсор мыши на конкретный график, чтобы видеть точки этого графика.

Возможно первым алгоритмом, используемым для аппроксимации , является метод, известный как вавилонский метод, несмотря на то, что нет никаких прямых свидетельств, за исключением гипотетических умозаключений, что вавилонские математики использовали этот метод^[6]. Метод известен также как метод Герона, по имени греческого математика первого столетия Герона, который дал первое явное описание метода в своей работе 60 года Метрика^[7].Основная методика заключается в том, что если x больше квадратного корня неотрицательного вещественного числа S то ${displaystyle {tfrac {S}{x}}}$ будет меньше корня и наоборот. Так что среднее этих двух чисел резонно ожидать более близким к корню (формальное доказательство этого факта основывается на неравенстве о среднем арифметическом, геометрическом и гармоническом, которое показывает, что это среднее всегда больше квадратного корня, что обеспечивает сходимость). Метод эквивалентен использованию метода Ньютона для решения уравнения ${displaystyle x^{2}-S=0}$ .

Точнее, если x является начальным приближением для , а ошибка в нашей оценке, такая что ${displaystyle S=(x+varepsilon )^{2}}$ , мы можем раскрыть скобки и получим

${displaystyle varepsilon ={frac {S-x^{2}}{2x+varepsilon }}approx {frac {S-x^{2}}{2x}},}$

поскольку

Следовательно, мы можем компенсировать ошибку и обновить нашу старую оценку

${displaystyle x+varepsilon approx x+{frac {S-x^{2}}{2x}}={frac {S+x^{2}}{2x}}={frac {{frac {S}{x}}+x}{2}}equiv x_{text{обновлённый}}}$

Поскольку вычисленная ошибка не была точной, она станет нашим следующим приближением. Процесс обновления продолжается пока не достигнем нужной точности. Это алгоритм с квадратичной сходимостью, что означает, что число верных цифр приближения (грубо говоря) удваивается с каждой итерацией. Работает он так:

Начинаем с любого положительного начального значения $x_{0}$ (чем ближе к истинному квадратному корню числа S, тем лучше).
Положим $x_{{n+1}}$ равным среднему между $x_{n}$ и ${displaystyle {tfrac {S}{x_{n}}}}$ (используем среднее арифметическое для аппроксимации среднего геометрического).
Повторяем шаг 2 пока не достигнем нужной точности.

Алгоритм можно представить следующим образом:

${displaystyle x_{0}approx {sqrt {S}},}$

${displaystyle x_{n+1}={frac {1}{2}}left(x_{n}+{frac {S}{x_{n}}}right),}$

${displaystyle {sqrt {S}}=lim _{nto infty }x_{n}.}$

Алгоритм работает также хорошо и для p-адических чисел, но не может быть использован для отождествления вещественных квадратных корней с p-адичными квадратными корнями. Можно, например, построить последовательность рациональных чисел, полученных этим методом, которая сходится к +3 в случае вещественных чисел, но к -3 в 2-адичных числах.

Пример[править | править код]

Для вычисления √S, где S = 125348, с точностью до шести значащих цифр используем метод грубой оценки, описанный выше

${displaystyle {begin{aligned}{begin{array}{rlll}x_{0}&=6cdot 10^{2}&&=600{,}000\[0,3em]x_{1}&={frac {1}{2}}left(x_{0}+{frac {S}{x_{0}}}right)&={frac {1}{2}}left(600{,}000+{frac {125348}{600{,}000}}right)&=404{,}457\[0.3em]x_{2}&={frac {1}{2}}left(x_{1}+{frac {S}{x_{1}}}right)&={frac {1}{2}}left(404{,}457+{frac {125348}{404{,}457}}right)&=357{,}187\[0.3em]x_{3}&={frac {1}{2}}left(x_{2}+{frac {S}{x_{2}}}right)&={frac {1}{2}}left(357{,}187+{frac {125348}{357{,}187}}right)&=354{,}059\[0.3em]x_{4}&={frac {1}{2}}left(x_{3}+{frac {S}{x_{3}}}right)&={frac {1}{2}}left(354{,}059+{frac {125348}{354{,}059}}right)&=354{,}045\[0.3em]x_{5}&={frac {1}{2}}left(x_{4}+{frac {S}{x_{4}}}right)&={frac {1}{2}}left(354{,}045+{frac {125348}{354{,}045}}right)&=354{,}045end{array}}end{aligned}}}$

Поэтому .

Сходимость[править | править код]

Предположим, что x₀ > 0 и S > 0. Тогда для любого n x_n > 0. Относительная ошибка^[en] x_n определена как

${displaystyle varepsilon _{n}={frac {x_{n}}{sqrt {S}}}-1>-1}$

а тогда

${displaystyle x_{n}={sqrt {S}}cdot (1+varepsilon _{n}).}$

Теперь можно показать, что

${displaystyle varepsilon _{n+1}={frac {varepsilon _{n}^{2}}{2(1+varepsilon _{n})}}geqslant 0.}$

а следовательно

${displaystyle varepsilon _{n+2}leqslant min left{{frac {varepsilon _{n+1}^{2}}{2}},{frac {varepsilon _{n+1}}{2}}right}}$

а отсюда следует гарантированная сходимость и эта сходимость квадратичная.

Сходимость в худшем случае[править | править код]

Если использовать метод грубой оценки с вавилонским методом, то наихудшие случаи точности в нисходящей последовательности:

${displaystyle {begin{aligned}S&=1;&x_{0}&=2;&x_{1}&=1{,}250;&varepsilon _{1}&=0{,}250.\S&=10;&x_{0}&=2;&x_{1}&=3{,}500;&varepsilon _{1}&<0{,}107.\S&=10;&x_{0}&=6;&x_{1}&=3{,}833;&varepsilon _{1}&<0{,}213.\S&=100;&x_{0}&=6;&x_{1}&=11{,}333;&varepsilon _{1}&<0{,}134.end{aligned}}}$

А тогда в любом случае

${displaystyle varepsilon _{1}leqslant 2^{-2}.,}$

${displaystyle varepsilon _{2}<2^{-5}<10^{-1}.,}$

${displaystyle varepsilon _{3}<2^{-11}<10^{-3}.,}$

${displaystyle varepsilon _{4}<2^{-23}<10^{-6}.,}$

${displaystyle varepsilon _{5}<2^{-47}<10^{-14}.,}$

${displaystyle varepsilon _{6}<2^{-95}<10^{-28}.,}$

${displaystyle varepsilon _{7}<2^{-191}<10^{-57}.,}$

${displaystyle varepsilon _{8}<2^{-383}<10^{-115}.,}$

Ошибки округления ослабляют сходимость. Рекомендуется хранить по меньшей мере одну лишнюю цифру выше желаемой точности x_n, чтобы минимизировать ошибки округления.

Метод Бакхшали[править | править код]

Этот метод для поиска приближения квадратного корня был написан в древнеиндийской рукописи, называемой манускриптом Бакхшали. Метод эквивалентен двум итерациям вавилонского метода с начальным значением x₀. Таким образом, алгоритм является квадратично сходящимся, что означает, что число верных знаков приближения увеличивается примерно в четыре раза с каждой итерацией^[8]. Представление алгоритма в современной нотации следующее: Следует вычислить , пусть x₀² будет начальным приближением к корню S. Последовательно выполняются итерации

${displaystyle {begin{aligned}a_{n}&={frac {S-x_{n}^{2}}{2x_{n}}},\b_{n}&=x_{n}+a_{n},\x_{n+1}&=b_{n}-{frac {a_{n}^{2}}{2b_{n}}}=(x_{n}+a_{n})-{frac {a_{n}^{2}}{2(x_{n}+a_{n})}}.end{aligned}}}$

Это можно использовать для построения рационального приближения к квадратному корню, начав с целого числа. Если ${displaystyle x_{0}=N}$ — это целое число, выбранное так, что N^2 близко к S, и ${displaystyle d=S-N^{2}}$ — это разность, абсолютная величина которой минимизируется, то первую итерацию можно записать следующим образом:

${displaystyle {sqrt {S}}approx N+{frac {d}{2N}}-{frac {d^{2}}{8N^{3}+4Nd}}={frac {8N^{4}+8N^{2}d+d^{2}}{8N^{3}+4Nd}}={frac {N^{4}+6N^{2}S+S^{2}}{4N^{3}+4NS}}={frac {N^{2}(N^{2}+6S)+S^{2}}{4N(N^{2}+S)}}.}$

Метод Бакхшали может быть обобщён для вычисления произвольного корня, включая дробные корни^[9].

Пример[править | править код]

Используем тот же пример, что был приведён для вавилонского метода. Пусть Тогда первая итерация даёт

${displaystyle {begin{aligned}x_{0}&=600\a_{1}&={frac {125348-600^{2}}{2times 600}}&&=&-195{,}543\b_{1}&=600+(-195{,}543)&&=&404{,}456\x_{1}&=404{,}456-{frac {(-195{,}543)^{2}}{2times 404{,}456}}&&=&357{,}186end{aligned}}}$

Аналогично вторая итерация даёт

${displaystyle {begin{aligned}a_{2}&={frac {125348-357{,}186^{2}}{2times 357{,}186}}&&=&-3{,}126\b_{2}&=357{,}186+(-3{,}126)&&=&354{,}060\x_{2}&=354{,}06-{frac {(-3{,}1269)^{2}}{2times 354{,}06}}&&=&354{,}046end{aligned}}}$

Цифра за цифрой[править | править код]

Это метод последовательного поиска каждой цифры квадратного корня. Метод медленнее вавилонского, но имеет некоторые преимущества

Он проще для вычислений вручную.
Каждый найденный знак корня заведомо верный, то есть он не будет изменён на следующих итерациях.
Если представление квадратного корня имеет конечное число цифр, алгоритм завершается после последней найденной цифры. Таким образом, он может быть использован для проверки, что данное число является полным квадратом.
Алгоритм работает в любой системе счисления, и естественно, работа алгоритма зависит от выбранной системы счисления.

Палочки Непера включают дополнительные средства для выполнения этого алгоритма. Алгоритм вычисления n-го корня цифра за цифрой^[en] является обобщением этого метода.

Основной принцип[править | править код]

Рассмотрим сначала случай нахождения квадратного корня из числа Z, являющегося квадратом двузначного числа XY, где X — это цифра десятков, а Y — цифра единиц. Имеем:

${displaystyle Z=(10X+Y)^{2}=100X^{2}+20XY+Y^{2}}$

Сначала определим значение X. X — это наибольшая цифра, такая что X² не превосходит Z, от которого отброшены две последние цифры.

На следующей итерации соединяем пару цифр, умножая X на 2 и помещая результат в позицию десятков, а затем пытаемся найти, чему же равно Y.

Поскольку в нашем случае ответом является точный квадратный корень, алгоритм останавливается.

Та же идея может быть распространена на вычисление произвольного квадратного корня. Представим, что мы можем найти квадратный корень из N как сумму n положительных чисел, таких что

${displaystyle N=(a_{1}+a_{2}+a_{3}+dotsb +a_{n})^{2}.}$

Путём многократного использования тождества

${displaystyle (x+y)^{2}=x^{2}+2xy+y^{2},}$

правую часть можно представить в виде

${displaystyle {begin{aligned}&(a_{1}+a_{2}+a_{3}+dotsb +a_{n})^{2}\=&,a_{1}^{2}+2a_{1}a_{2}+a_{2}^{2}+2(a_{1}+a_{2})a_{3}+a_{3}^{2}+dotsb +a_{n-1}^{2}+2left(sum _{i=1}^{n-1}a_{i}right)a_{n}+a_{n}^{2}\=&,a_{1}^{2}+[2a_{1}+a_{2}]a_{2}+[2(a_{1}+a_{2})+a_{3}]a_{3}+dotsb +left[2left(sum _{i=1}^{n-1}a_{i}right)+a_{n}right]a_{n}.end{aligned}}}$

Это выражение позволяет нам найти квадратный корень последовательным подбором значений $a_{i}$ . Предположим, что числа ${displaystyle a_{1},ldots ,a_{m-1}}$ уже подобраны, тогда m-й член задаётся выражением ${displaystyle Y_{m}=[2P_{m-1}+a_{m}]a_{m},}$ , где ${displaystyle P_{m-1}=sum _{i=1}^{m-1}a_{i}}$ является найденным приближением к квадратному корню. Теперь каждый новый подбор a_m должен удовлетворять рекурсии

${displaystyle X_{m}=X_{m-1}-Y_{m},}$

так что ${displaystyle X_{m}geqslant 0}$ для всех при начальном значении ${displaystyle X_{0}=N.}$ Если ${displaystyle X_{n}=0,}$ найден точный квадратный корень. Если нет, то сумма $a_{i}$ даёт подходящую аппроксимацию к квадратному корню и X_n будет ошибкой аппроксимации.

Например, в десятичной системе мы имеем

${displaystyle N=(a_{1}cdot 10^{n-1}+a_{2}cdot 10^{n-2}+cdots +a_{n-1}cdot 10+a_{n})^{2},}$

где ${displaystyle 10^{n-i}}$ являются указателями положения цифр, а коэффициенты ${displaystyle a_{i}in {0,1,2,ldots ,9}}$ . На каждом m-м шаге вычисления квадратного корня находится приближённый квадратный корень. Величина ${displaystyle P_{m-1}}$ и суммируемые члены $Y_{m}$ задаются формулами

${displaystyle P_{m-1}=sum _{i=1}^{m-1}a_{i}cdot 10^{n-i}=10^{n-m+1}sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1},}$

${displaystyle Y_{m}=[2P_{m-1}+a_{m}cdot 10^{n-m}]a_{m}cdot 10^{n-m}=left[20sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1}+a_{m}right]a_{m}cdot 10^{2(n-m)}.}$

Поскольку указатели положения $Y_{m}$ имеют чётную степень 10, нам нужно работать только с парой старших цифр в оставшемся члене ${displaystyle X_{m-1}}$ на любом m-м шаге. Раздел ниже систематизирует эту процедуру.

Очевидно, что подобный метод может быть использован для вычисления квадратного корня в любой системе счисления, не обязательно в десятичной. Например, нахождение цифра за цифрой квадратного корня в двоичной системе довольно эффективно, поскольку значение $a_{i}$ ищется в малом наборе цифр {0,1}. Это делает вычисление более быстрым, поскольку на каждом шаге значение $Y_{m}$ либо равно ${displaystyle Y_{m}=0}$ для ${displaystyle a_{m}=0}$ , либо ${displaystyle Y_{m}=2P_{m-1}+1}$ для ${displaystyle a_{m}=1}$ . Факт, что имеется всего две возможности для a_m также делает проще процесс выбора значения a_m на m-м шаге вычислений. Это потому, что нам нужно лишь проверить, что ${displaystyle Y_{m}leqslant X_{m-1}}$ для ${displaystyle a_{m}=1.}$ Если это условие выполняется, мы берём ${displaystyle a_{m}=1}$ ; а если не выполняется, то берём ${displaystyle a_{m}=0.}$ Также факт, что умножение на 2 осуществляется сдвигом влево, помогает при вычислениях.

Десятичная система счисления[править | править код]

Запишем исходное число в десятичном виде. Числа, записываются по аналогии алгоритму деления столбиком, и, как и в длинном делении, квадратный корень будет писаться в верхней строке. Теперь разобьём цифры на пары, начиная с запятой, в обе стороны от неё. Десятичная запятая квадратного корня будет на десятичной запятой квадрата. Одна цифра квадратного корня записывается над парой цифр квадрата.

Начиная с крайне левой позиции выполняем следующую процедуру для каждой пары цифр:

Сносим вниз старшую пару ещё неиспользованных цифр (если все цифры использованы, пишем “00”) и записываем их справа от остатка предыдущего шага (на первом шаге остатка нет). Другими словами, умножаем остаток на 100 и добавляем две цифры. Это будет текущим значением c.
Находим p, y и x следующим образом:
Вычитаем y из c для образования нового остатка.
Если остаток равен нулю и нет больше цифр, которые можно спустить вниз, алгоритм останавливается. В противном случае возвращаемся на шаг 1 и выполняем следующую итерацию.

Примеры[править | править код]

Находим квадратный корень из 152,2756.

          1  2. 3  4 
       /
     /  01 52,27 56

         01                   1*1 <= 1 < 2*2                 x = 1
         01                     y = x*x = 1*1 = 1
         00 52                22*2 <= 52 < 23*3              x = 2
         00 44                  y = (20+x)*x = 22*2 = 44
            08 27             243*3 <= 827 < 244*4           x = 3
            07 29               y = (240+x)*x = 243*3 = 729
               98 56          2464*4 <= 9856 < 2465*5        x = 4
               98 56            y = (2460+x)*x = 2464*4 = 9856
               00 00          Алгоритм останавливается: Ответ 12,34

Двоичная система счисления[править | править код]

Этот раздел использует формализм раздела «Вычисление цифра за цифрой» с небольшими изменениями, что ${displaystyle N^{2}=(a_{n}+dotsb +a_{0})^{2}}$ , а каждое a_m равно $2^{m}$ или .
Теперь мы пробегаем по всем $2^{m}$ от $2^{n}$ вниз до 2^0 и строим приближённое решение ${displaystyle P_{m}=a_{n}+a_{n-1}+ldots +a_{m}}$ в виде суммы всех $a_{i}$ , для которых мы найдём значение.
Чтобы определить, равно ли a_m значению $2^{m}$ или , мы берём ${displaystyle P_{m}=P_{m+1}+2^{m}}$ . Если ${displaystyle P_{m}^{2}leqslant N^{2}}$ (то есть квадрат нашего приближения включая $2^{m}$ не превосходит исходного квадрата), то полагаем ${displaystyle a_{m}=2^{m}}$ , в противном случае полагаем ${displaystyle a_{m}=0}$ и ${displaystyle P_{m}=P_{m+1}}$ .
Чтобы избежать возведения в квадрат ${displaystyle P_{m}}$ на каждом шаге, мы запоминаем разность ${displaystyle X_{m}=N^{2}-P_{m}^{2}}$ и обновляем её на каждой итерации, полагая ${displaystyle X_{m}=X_{m+1}-Y_{m}}$ с ${displaystyle Y_{m}=P_{m}-P_{m+1}=2P_{m+1}a_{m}+a_{m}^{2}}$ .
Первоначально мы устанавливаем ${displaystyle a_{n}=P_{n}=2^{n}}$ для наибольшего с ${displaystyle (2^{n})^{2}=4^{n}leqslant N^{2}}$ .

В качестве дополнительной оптимизации сохраняем ${displaystyle P_{m+1}2^{m+1}}$ и ${displaystyle (2^{m})^{2}}$ , два члена $Y_{m}$ в случае, когда a_m не нуль, в отдельных переменных ${displaystyle c_{m}}$ , ${displaystyle d_{m}}$ :

${displaystyle c_{m}=P_{m+1}2^{m+1}}$

${displaystyle d_{m}=(2^{m})^{2}}$

${displaystyle Y_{m}={begin{cases}c_{m}+d_{m}&{text{если }}a_{m}=2^{m}\0&{text{если }}a_{m}=0end{cases}}}$

${displaystyle c_{m}}$ и ${displaystyle d_{m}}$ можно эффективно обновлять на каждом шаге:

${displaystyle c_{m-1}=P_{m}2^{m}=(P_{m+1}+a_{m})2^{m}=P_{m+1}2^{m}+a_{m}2^{m}={begin{cases}c_{m}/2+d_{m}&{text{если }}a_{m}=2^{m}\c_{m}/2&{text{если }}a_{m}=0end{cases}}}$

${displaystyle d_{m-1}={frac {d_{m}}{4}}}$

Заметим, что

${displaystyle c_{-1}=P_{0}2^{0}=P_{0}=N}$

, что является конечным результатом, возвращаемым функцией, представленной ниже.

Реализация алгоритма на языке C^[10]:

int32_t isqrt(int32_t n) 
{ assert(("входное значение должно быть неотрицательным", n > 0));
  int32_t x = n;    // 
  int32_t c = 0;    // 
  //  начинается с наибольшей степени четырёх <= n
  int32_t d = 1 << 30; // Второй старший бит устанавливаем в 1.
                        // То же самое, что ((unsigned)INT32_MAX + 1) / 2.
  while (d > n) d >>= 2;
  while (d != 0)    // для 
  { if (x >= c + d) // если , то 
    { x -= c + d;       // 
     c = (c >> 1) + d;  // 
   } else
          c >>= 1;      // 
    d >>= 2;            // 
  }
  return c;             // 
}

Можно реализовать более быстрый алгоритм как в двоичной, так и в десятичной системе счисления, если использовать таблицы для выбора, то есть реализация принципа использование больше памяти сокращает время исполнения^[11].

Экспоненциальное тождество[править | править код]

Карманные калькуляторы обычно реализуют хорошие программы вычисления экспоненты и натурального логарифма. Вычисление квадратного корня S тогда производится с помощью свойств логарифмов ( ${displaystyle ln x^{n}=nln x}$ ) и экспоненты ( ${displaystyle e^{ln x}=x}$ ):

${displaystyle {sqrt {x}}=e^{{frac {1}{2}}ln x},,x>0.}$

Или в более общем случае:

${displaystyle {sqrt[{n}]{x}}=e^{{frac {1}{n}}ln x},,x>0.}$

Знаменатель дроби n соответствует степени корня. В случае квадратного корня знаменатель равен 2. То же самое тождество используется для вычисления квадратного корня с помощью таблиц логарифмов или логарифмических линеек.

Такой метод вычисления квадратного корня удобен для калькуляторов, поскольку они обычно не критичны ко времени выполнения операции. Однако ресурсоемкость данного метода делает его малопригодным для использования в ЭВМ, где простые арифметические операции должны обладать минимальными задержками. Тем не менее описанный метод вычисления квадратного корня применялся в ЭВМ ZX Spectrum.

Итеративный метод с двумя переменными[править | править код]

Этот метод применим для поиска квадратного корня из и лучше всего сходится для .
Это, однако, не является существенным ограничением для вычислений на компьютерах, поскольку в представлениях двоичных чисел с плавающей запятой и с фиксированной запятой тривиально умножить на целую степень числа 4, с последующей коррекцией на нужную степень 2 путём изменения экспоненты или сдвигом соответственно. Таким образом, может быть сдвинуто в пределы ${displaystyle {frac {1}{2}}leqslant S<2}$ . Более того, приведённый ниже метод не использует делений общего вида, а только сложение, вычитание, умножение и деление на степень двойки. Последнее из этих действий тривиально реализуется. Недостатком метода является накопление ошибки, в отличие от итеративных методов с одной переменной, таких как вавилонский.

Начальный шаг метода

${displaystyle a_{0}=S,!}$

${displaystyle c_{0}=S-1,!}$

Итерационные шаги

${displaystyle a_{n+1}=a_{n}-a_{n}c_{n}/2,!}$

${displaystyle c_{n+1}=c_{n}^{2}(c_{n}-3)/4,!}$

Тогда ${displaystyle a_{n}rightarrow {sqrt {S}}}$ (при ${displaystyle c_{n}rightarrow 0}$ ).

Заметим, что сходимость ${displaystyle c_{n},!}$ , а потому и ${displaystyle a_{n},!}$ , квадратична.

Доказательство метода достаточно простое. Сначала перепишем итерационное определение ${displaystyle c_{n},!}$ как

${displaystyle 1+c_{n+1}=(1+c_{n})(1-c_{n}/2)^{2},!}$

Теперь «в лоб» доказывается, что

${displaystyle S(1+c_{n})=a_{n}^{2}}$

а потому сходимость ${displaystyle a_{n},!}$ к желаемому результату обеспечивается сходимостью ${displaystyle c_{n},!}$ к 0, что, в свою очередь, вытекает из ${displaystyle -1<c_{0}<2,!}$ .

Этот метод разработали около 1950 года М. В. Уилкс, Д. Дж. Уилер и С. Гилл^[12] для использования в EDSAC, одном из первых электронных компьютеров^[13]. Позднее метод был обобщён на неквадратные корни^[14].

Итеративные методы вычисления обратного к квадратному корню числа[править | править код]

Далее приведены итеративные методы вычисления обратного к квадратному корню из S числа, то есть . Если такое значение найдено, находим просто умножением: . Эти итерации используют только умножение и не используют деления. Потому методы быстрее, чем вавилонский метод. Однако методы нестабильны, если начальное значение не близко к обратному к корню значению, итерации расходятся. Поэтому может быть выгодным сначала сделать итерацию вавилонским методом для грубой оценки корня перед началом использования этих методов.

Алгоритм Гольдшмидта[править | править код]

Некоторые компьютеры используют алгоритм Гольдшмидта для одновременного вычисления и .
Алгоритм Гольдшмидта находит быстрее, чем итерация Ньютона-Рапсона, на компьютерах с операциями совмещённого умножения-сложения и имеющих либо конвейерный процессор плавающей запятой, либо два независимых процессора плавающей запятой^[15].

Первый способ записи алгоритма Гольдшмидта начинается с

${displaystyle b_{0}=S}$

${displaystyle Y_{0}approx 1/{sqrt {S}}}$

(обычно используется поиск в таблице)

${displaystyle y_{0}=Y_{0}}$

${displaystyle x_{0}=Sy_{0}}$

и осуществляются итерации

${displaystyle b_{n+1}=b_{n}Y_{n}^{2}}$

${displaystyle Y_{n+1}=(3-b_{n+1})/2}$

${displaystyle x_{n+1}=x_{n}Y_{n+1}}$

${displaystyle y_{n+1}=y_{n}Y_{n+1}}$

пока $b_{i}$ не окажется достаточно близко к 1 или не будет проведено фиксированное число итераций. Итерации сходятся к

${displaystyle lim _{nto infty }x_{n}={sqrt {S}}}$

${displaystyle lim _{nto infty }y_{n}=1/{sqrt {S}}}$

Заметим, что можно опустить вычисление $x_{n}$ или $y_{n}$ , а если оба значения желательны, то ${displaystyle x_{n}=Sy_{n}}$ можно использовать в конце вместо вычисления на каждой итерации.

Второй способ, использующий операции совмещённого умножения-сложения начинается с

${displaystyle y_{0}approx 1/{sqrt {S}}}$

(обычно используется поиск в таблице)

${displaystyle x_{0}=Sy_{0}}$

${displaystyle h_{0}=y_{0}/2}$

и осуществляются итерации

${displaystyle r_{n}=0{,}5-x_{n}h_{n}}$

${displaystyle x_{n+1}=x_{n}+x_{n}r_{n}}$

${displaystyle h_{n+1}=h_{n}+h_{n}r_{n}}$

пока $r_{i}$ не станет достаточно близко к 0, либо не будет осуществлено фиксированное число итераций. Значения сходятся к

${displaystyle lim _{nto infty }x_{n}={sqrt {S}}}$

${displaystyle lim _{nto infty }2h_{n}=1/{sqrt {S}}}$

Ряды Тейлора[править | править код]

Если N является приближением к , лучшее приближения может быть найдено использованием ряда Тейлора функции квадратного корня:

${displaystyle {sqrt {N^{2}+d}}=Nsum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)n!^{2}4^{n}}}{frac {d^{n}}{N^{2n}}}=Nleft(1+{frac {d}{2N^{2}}}-{frac {d^{2}}{8N^{4}}}+{frac {d^{3}}{16N^{6}}}-{frac {5d^{4}}{128N^{8}}}+cdots right)}$

Порядок сходимости равен числу используемых членов ряда. При использовании двух членов метод эквивалентен вавилонскому методу. При использовании трёх членов каждая итерация использует почти столько же операций, сколько использует приближение Бакхшали, но сходимость слабее. Поэтому этот метод не является особенно эффективным способом вычисления. Для максимизации скорости сходимости, следует выбрать N так, чтобы ${displaystyle {frac {|d|}{N^{2}}},}$ было как можно меньше.

Разложение в цепную дробь[править | править код]

Квадратичные иррациональности (числа вида ${displaystyle {frac {a+{sqrt {b}}}{c}}}$ , где a, b и c целые числа), и, в частности, квадратные корни из целых чисел, имеют периодические цепные дроби^[en]. Иногда целью является не нахождение численного значения квадратного корня, а его разложение в цепную дробь, а следовательно его рационального приближения. Пусть S будет положительным числом, корень из которого требуется найти. Теперь пусть a будет начальным приближением, а r будет остаточным членом, тогда мы можем записать ${displaystyle S=a^{2}+r.}$ Поскольку мы имеем ${displaystyle S-a^{2}=({sqrt {S}}+a)({sqrt {S}}-a)=r}$ , мы можем выразить квадратный корень из S как

${displaystyle {sqrt {S}}=a+{frac {r}{a+{sqrt {S}}}}.}$

Применяя это выражение для к знаменателю дроби, получим

${displaystyle {sqrt {S}}=a+{frac {r}{a+(a+{frac {r}{a+{sqrt {S}}}})}}=a+{frac {r}{2a+{frac {r}{a+{sqrt {S}}}}}}.}$

Компактная запись

Числитель/знаменатель разложения для непрерывных дробей (см. слева) затруднительно записывать, а также трудно укладывается в существующую систему форматирования документов. По этой причине была разработана специальная нотация для компактного представления целой и периодической частей непрерывных дробей. Одно из таких соглашений использует лексическую «ломаную линию» для представления черты между числителем и знаменателем, что позволяет записывать дробь горизонтально, а не вертикально:

${displaystyle {sqrt {S}}=a+{frac {r|}{|2a}}+{frac {r|}{|2a}}+{frac {r|}{|2a}}+cdots }$

Здесь каждая горизонтальная черта (в дроби) представлена тремя чертами — двумя вертикальными и одной горизонтальной, которые отделяют от .

Ещё более компактная нотация имеет специальный вид

Для периодических непрерывных дробей (которыми являются все квадратные корни), повторяющаяся часть указывается лишь один раз с чертой над повторяющейся частью:

Для √2 значение равно 1, так что представлением будет

Следуя этим путём мы получаем обобщённую непрерывную дробь^[en] для квадратного корня
${displaystyle {sqrt {S}}=a+{cfrac {r}{2a+{cfrac {r}{2a+{cfrac {r}{2a+ddots }}}}}}}$

Первым шагом вычисления такой дроби для получения квадратного корня является подстановки для корня и выбор числа знаменателей. Например, в канонической форме равен 1 и для √2, равен 1, так что численно непрерывной дробью для 3 знаменателей будет

${displaystyle {sqrt {2}}approx 1+{cfrac {1}{2+{cfrac {1}{2+{cfrac {1}{2}}}}}}}$

Шаг 2. Непрерывная дробь свёртывается снизу вверх, один знаменатель за раз, чтобы получить рациональную дробь, числитель и знаменатель которой являются целыми числами. Процесс свёртывания тогда выглядит следующим образом (беря первые три знаменателя):

${displaystyle 1+{cfrac {1}{2+{cfrac {1}{2+{cfrac {1}{2}}}}}}=1+{cfrac {1}{2+{cfrac {1}{frac {5}{2}}}}}}$

${displaystyle =1+{cfrac {1}{2+{cfrac {2}{5}}}}=1+{cfrac {1}{frac {12}{5}}}}$

${displaystyle =1+{cfrac {5}{12}}={frac {17}{12}}}$

Наконец (шаг 3), делим числитель на знаменатель рациональной дроби, чтобы получить приближённое значение корня:

округлено до трёх знаков.

Действительное значение корня √2 равно 1,41 с точностью до трёх значащих цифр. Относительная ошибка равна 0,17%, так что рациональная дробь хороша почти до трёх знаков. Если брать больше знаменателей, получим последовательное улучшение приближения — четыре знаменателя дают дробь ${displaystyle {frac {41}{29}}=1{,}4137}$ , что даёт почти 4 цифры точности, и т.д.

Непрерывные дроби доступны в таблицах по меньшей мере для малых чисел и общеизвестных констант. Для произвольных чисел в десятичной системе счисления предварительно вычисленные значения, скорее всего, бесполезны. Следующая таблица малых рациональных дробей, называемых подходящими дробями, полученных из канонических непрерывных дробей для нескольких констант:

√S	~десятичное	Подходящие дроби
√2	1,41421	${displaystyle {frac {3}{2}},{frac {7}{5}},{frac {17}{12}},{frac {41}{29}},{frac {99}{70}}}$
√3	1,73205	${displaystyle {frac {2}{1}},{frac {5}{3}},{frac {7}{4}},{frac {19}{11}},{frac {26}{15}},{frac {71}{41}},{frac {97}{56}}}$
√5	2,23607	${displaystyle {frac {9}{4}},{frac {38}{17}},{frac {161}{72}}}$
√6	2,44949	${displaystyle {frac {5}{2}},{frac {22}{9}},{frac {49}{20}},{frac {218}{89}}}$
√10	3,16228	${displaystyle {frac {19}{6}},{frac {117}{37}}}$
	1,77245	${displaystyle {frac {2}{1}},{frac {7}{4}},{frac {16}{9}},{frac {23}{13}},{frac {39}{22}}}$
	1,64872	${displaystyle {frac {2}{1}},{frac {3}{2}},{frac {5}{3}},{frac {28}{17}},{frac {33}{20}},{frac {61}{37}}}$
	1,27202	${displaystyle {frac {4}{3}},{frac {5}{4}},{frac {14}{11}}}$

Примечание: Перечислены все подходящие дроби вплоть до знаменателя 99.

В общем виде чем больше знаменатель рациональной дроби, тем лучше аппроксимация. Также можно доказать, что отсечение непрерывной дроби приводит к рациональной дроби, с лучшим приближением к корню любой дроби со знаменателем, меньшим или равным знаменателю этой дроби. Например, никакая дробь со знаменателем, не превосходящем 70, не будет так же хороша, как аппроксимация к √2 числом 99/70.

Метод последовательности Люка[править | править код]

Последовательность Люка первого рода ${displaystyle U_{n}(P,Q)}$ определяется рекуррентным отношением

${displaystyle U_{n}(P,Q)={begin{cases}0&{text{если }}n=0\1&{text{если }}n=1\Pcdot U_{n-1}(P,Q)-Qcdot U_{n-2}(P,Q)&{text{в противном случае}}end{cases}}}$

и его характеристическим многочленом является

${displaystyle x^{2}-Pcdot x+Q=0}$

, он имеет дискриминант ${displaystyle D=P^{2}-4Q}$ и корни

${displaystyle {begin{matrix}x_{1}={dfrac {P+{sqrt {D}}}{2}},&x_{2}={dfrac {P-{sqrt {D}}}{2}}end{matrix}}}$

Всё это даёт следующее положительное значение

${displaystyle lim _{nto infty }{dfrac {U_{n+1}}{U_{n}}}=x_{1}}$

. Так что если мы хотим получить , мы можем выбрать и , а затем вычислить ${displaystyle x_{1}=1+{sqrt {a}}}$ используя ${displaystyle U_{n+1}}$ и $U_{n}$ для больших значений .
Наиболее эффективный способ вычисления ${displaystyle U_{n+1}}$ и $U_{n}$ —

${displaystyle {begin{bmatrix}U_{n}\U_{n+1}end{bmatrix}}={begin{bmatrix}0&1\-Q&Pend{bmatrix}}cdot {begin{bmatrix}U_{n-1}\U_{n}end{bmatrix}}={begin{bmatrix}0&1\-Q&Pend{bmatrix}}^{n}cdot {begin{bmatrix}U_{0}\U_{1}end{bmatrix}}}$

Итог:

${displaystyle {begin{bmatrix}0&1\a-1&2end{bmatrix}}^{n}cdot {begin{bmatrix}0\1end{bmatrix}}={begin{bmatrix}U_{n}\U_{n+1}end{bmatrix}},}$

а тогда при :

${displaystyle {sqrt {a}}={frac {U_{n+1}}{U_{n}}}-1}$

Аппроксимации, зависящие от представления в виде числа с плавающей запятой[править | править код]

Число представляется в виде числа с плавающей запятой как ${displaystyle mtimes b^{p}}$ . Этот формат записи называется также экспоненциальной записью. Квадратный корень из этого числа равен ${displaystyle {sqrt {m}}times b^{tfrac {p}{2}}}$ и аналогичные формулы могут быть представлены для кубических корней и логарифмов. Это не упрощает задачу, но если требуется только аппроксимация, то ${displaystyle b^{tfrac {p}{2}}}$ является хорошей оценкой порядка мантиссы. Далее, понимаем, что некоторые степени p могут оказаться нечётными, тогда для ${displaystyle 3141{,}59=3{,}14159{times }10^{3}}$ вместо работы с дробными степенями основания умножаем на него и вычитаем единицу из степени, делая её чётной. Уточнённое представление превращается в ${displaystyle 31{,}4159{times }10^{2}}$ , так что квадратный корень будет равен ${displaystyle {sqrt {31,4159}}{times }10^{1}}$ .

Если взять лишь целую часть мантиссы, она может принимать значения от 1 до 99 и это можно использовать в качестве индекса в таблице из 99 предварительно вычисленных корней для завершения оценки. Компьютер, использующий шестнадцатеричное основание может потребовать большей таблицы, но при использовании основания 2 таблица будет состоять лишь из трёх величин — возможными битами целой части уточнённого представления мантиссы могут быть 01 (если степень чётная, так что нет никакого сдвига, и заметим, что нормализованное число с плавающей точкой всегда имеет ненулевую старшую цифру), или, если степень была нечётной, 10 или 11, это два первых бита исходной мантиссы. Тогда 6,25 (= 110,01 в двоичном представлении) нормализуется к ${displaystyle 1{,}1001times 2^{2}}$ с чётной степенью, так что парой битов мантиссы будет 01, в то время как 0,625 (= 0,101 в двоичном представлении) нормализуется к ${displaystyle 1{,}01times 2^{-1}}$ с нечётной степенью, так что требуется преобразование числа к ${displaystyle 10{,}1times 2^{-2}}$ , а тогда парой бит будет 10. Заметим, что младший бит порядка отражается в старший бит сгруппированной парами мантиссы. Чётная степень имеет нулевой младший бит и уточнённая мантисса будет начинаться с нуля, в то время как нечётная степень имеет 1 в младшем бите и уточнённая мантисса будет начинаться с 1. Таким образом, когда степень делится пополам, это эквивалентно тому, что младший бит порядка сдвигается в первый бит попарно сгруппированной мантиссы.

Таблица с тремя элементами может быть расширена для включения дополнительных бит мантиссы. Однако в случае компьютеров вместо вычисления интерполяции в таблице часто лучше искать более простой способ вычислений, дающий те же результаты. Всё теперь зависит от точных деталей формата представления чисел и от операций, которые доступны для получения частей числа и работы с ними. Например, Фортран содержит функцию EXPONENT(x) для получения степени. Усилия, потраченные на получение хорошего начального приближения окупаются за счёт исключения дополнительных итераций процесса уточнения, которые потребовались бы в случае плохого приближения.

Многие компьютеры следуют стандарту IEEE для чисел с плавающей запятой^[en] (или достаточно близкое представление) и очень быстрое приближение для квадратного корня может быть получено в качестве стартового значения метода Ньютона. Техника данного приближения вытекает из факта, что формат плавающего числа (по основанию два) аппроксимирует логарифм по основанию 2. То есть, ${displaystyle log _{2}(mtimes 2^{p})=p+log _{2}(m)}$

Так что для 32-битного числа с плавающей запятой в формате IEEE (в котором степень имеет смещение^[en] на 127^[16]) вы можете получить приближённый логарифм путём интерпретации числа как 32-битного целого, умножения его на ${displaystyle 2^{-23}}$ и вычета смещения 127, то есть

${displaystyle x_{text{int}}cdot 2^{-23}-127approx log _{2}(x).}$

Например, число 1,0 в шестнадцатеричной системе имеет вид 0x3F800000, что можно представить как ${displaystyle 1065353216=127cdot 2^{23}}$ , если рассматривать его как целое. Используя вышеприведённую формулу вы получите ${displaystyle 1065353216cdot 2^{-23}-127=0}$ , как и ожидалось от ${displaystyle log _{2}(1{,}0)}$ . Аналогичным образом вы получите 0,5 из 1,5 (=0x3FC00000).

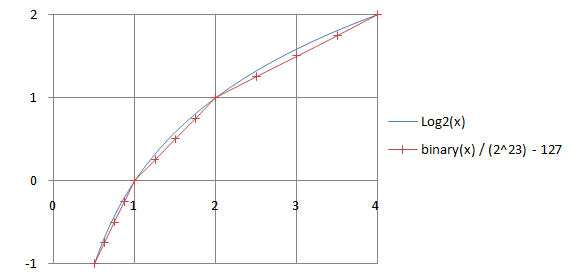
Чтобы получить квадратный корень, делим логарифм на 2 и преобразуем результат обратно. Ниже программа демонстрирует идею. Заметим, что младший бит порядка намеренно переводится в мантиссу. Одним из способов обоснования шагов этой программы, в предположении что является смещением степени, а является числом запоминаемых бит в мантиссе, заключается в доказательстве

${displaystyle (((x_{text{int}}/2^{n}-b)/2)+b)cdot 2^{n}=(x_{text{int}}-2^{n})/2+((b+1)/2)cdot 2^{n}.}$

/* Предполагаем, что плавающее число имеет формат IEEE 754 */
#include <stdint.h>
float sqrt_approx(float z)
{
	union { float f; uint32_t i; } val = {z};	/* Преобразуем тип не меняя битового представления */
	/*
	 * Для обоснования работы кода докажите, что
	 * ((((val.i / 2^m) - b) / 2) + b) * 2^m = ((val.i - 2^m) / 2) + ((b + 1) / 2) * 2^m)
	 * где
	 * b = смещение степени
	 * m = число бит в мантиссе
	 */
	val.i -= 1 << 23;	/* Вычитаем 2^m. */
	val.i >>= 1;		/* Делим на 2. */
	val.i += 1 << 29;	/* Добавляем ((b + 1) / 2) * 2^m. */

	return val.f;		/* Интерпретируем снова как плавающее */
}

Три арифметические операции, образующие ядро функции можно представить в одну строку. Дополнительное уточнение может быть добавлено для уменьшения максимальной относительной ошибки. Таким образом, три операции, не включая приведение к вещественному, можно переписать как

	val.i = (1 << 29) + (val.i >> 1) - (1 << 22) + a;

где a — смещение для уменьшения ошибок аппроксимации. Например, с a = 0 результаты точны для чётных степеней двойки 2 (например, 1,0), но для других чисел результат будет несколько великоват (например, 1,5 для 2,0 вместо 1,414… с ошибкой 6%). При a = −0x4B0D2 максимальная относительная ошибка сокращается до ±3,5%.

Если приближение нужно использовать как начальное значение для метода Ньютона в уравнении ${displaystyle (1/x^{2})-S=0}$ , то обратная форма, показанная в следующем разделе, предпочтительнее.

Обратное значение квадратного корня[править | править код]

Вариант описанной выше процедуры представлен ниже и он может быть использован для вычисления обратного к квадратному корню, то есть ${displaystyle x^{-{1 over 2}}}$ . Этот вариант написал Грег Уолш. Приближение сдвигом даёт относительную ошибку менее 4% и ошибка уменьшается до 0,15% после одной итерации метода Ньютона^[17]. В компьютерной графике это очень эффективный способ нормализации вектора.

float invSqrt(float x) {
    float xhalf = 0.5f * x;
    union {
        float x;
        int i;
    } u;
    u.x = x;
    u.i = 0x5f375a86 - (u.i >> 1);
    /* Следующая строка может быть повторена произвольное число раз для увеличения точности */
    u.x = u.x * (1.5f - xhalf * u.x * u.x);
    return u.x;
}

Некоторые СБИС реализуют нахождение обратной величины к квадратному корню с помощью полиномиальной оценки с последующей итерацией Голдшмидта^[18].

Корень из отрицательного или комплексного числа[править | править код]

Если S<0 , то его главный корень равен

{displaystyle {sqrt {S}}={sqrt {vert Svert }},,i,.}

Если , где a и b вещественные числа и bneq 0 , то его главный корень равен

${displaystyle {sqrt {S}}={sqrt {frac {vert Svert +a}{2}}},+,operatorname {sgn}(b){sqrt {frac {vert Svert -a}{2}}},,i,.}$

Это можно проверить возведением в квадрат^[19]^[20]. Здесь

${displaystyle vert Svert ={sqrt {a^{2}+b^{2}}}}$

является модулем числа S. Главный корень комплексного числа определяется как корень с неотрицательной вещественной частью.

См. также[править | править код]

Алгоритм альфа max плюс бета min^[en]
Целочисленный квадратный корень

Примечания[править | править код]

↑ Кроме главного корня имеется отрицательный квадратный корень, равный по модулю главному корню, но с противоположным знаком, за исключением случая нуль, когда имеется два одинаковых корня, равных нулю.
↑ Множители два и шесть используются ввиду того, что они аппроксимируют среднее геометрическое нижнего и верхнего возможных значений с заданным числом знаков: и .
↑ Неокруглённая оценка имеет максимальную абсолютную ошибку 2,65 в точке 100 и максимальную относительную ошибку в 26,5% в точках y=1, 10 и 100
↑ Если число находится ровно посередине между двумя квадратами, наподобие 30,5, берём большее число, которое в нашем случае 6
↑ Это уравнение касательной прямой к y=x² в точке y=1.
↑ Fowler, Robson, 1998, с. 376.
↑ Heath, 1921, с. 323–324.
↑ Bailey, Borwein, 2012, с. 646–657.
↑ Bucking down to the Bakhshali manuscript. Simply Curious blog (5 июня 2018). Дата обращения: 21 декабря 2020. Архивировано 26 октября 2020 года.
↑ Fast integer square root by Mr. Woo’s abacus algorithm (archived)
↑ Integer Square Root function. Дата обращения: 30 декабря 2021. Архивировано 30 сентября 2007 года.
↑ Wilkes, Wheeler, Gill, 1951.
↑ Campbell-Kelly, 2009.
↑ Gower, 1958, с. 142–143, 1958.
↑ Markstein, Peter (November 2004). Software Division and Square Root Using Goldschmidt’s Algorithms (PDF). 6th Conference on Real Numbers and Computers. Dagstuhl, Germany. CiteSeerX 10.1.1.85.9648. Архивировано (PDF) из оригинала 2022-04-28. Дата обращения 2021-12-30.
↑ К экспоненте числа добавляется 127, что позволяет интерпретировать экспоненту как число без знака.
↑ Fast Inverse Square Root Архивная копия от 6 февраля 2009 на Wayback Machine by Chris Lomont
↑
“High-Speed Double-Precision Computation of Reciprocal, Division, Square Root and Inverse Square Root”
by José-Alejandro Piñeiro and Javier Díaz Bruguera 2002 (abstract)
↑ Abramowitz, Stegun, 1964, с. 17.
↑ Cooke, 2008, с. 59.

Литература[править | править код]

David Fowler, Eleanor Robson. Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context // Historia Mathematica. — 1998. — Т. 25, вып. 4. — doi:10.1006/hmat.1998.2209.
Thomas Little Heath. A History of Greek Mathematics. — Oxford: Clarendon Press, 1921. — Т. 2. — С. 323–324.
David Bailey, Jonathan Borwein. Ancient Indian Square Roots: An Exercise in Forensic Paleo-Mathematics // American Mathematical Monthly. — 2012. — Т. 119, вып. 8.
Miltonn Abramowitz, Irene A. Stegun. Section 3.7.26 // Handbook of mathematical functions with formulas, graphs, and mathematical tables. — Courier Dover Publications, 1964. — С. 17. — ISBN 978-0-486-61272-0.
J. C. Gower. A Note on an Iterative Method for Root Extraction // The Computer Journal. — 1958. — Т. 1 1, вып. 3.
M. Campbell-Kelly. Origin of Computing // Scientific American. — 2009. — Сентябрь.
Roger Cooke. Classical algebra: its nature, origins, and uses. — John Wiley and Sons, 2008. — ISBN 978-0-470-25952-8.
M. V. Wilkes, D. J. Wheeler, S. Gill. The Preparation of Programs for an Electronic Digital Computer. — Addison-Wesley, 1951.

СсылкиWeisstein, Eric W. Square root algorithms (англ.) на сайте Wolfram MathWorld.[править | править код]

Square roots by subtraction
Integer Square Root Algorithm by Andrija Radović
Personal Calculator Algorithms I : Square Roots (William E. Egbert), Hewlett-Packard Journal (may 1977) : page 22
Калькулятор для обучения квадратному корню

Источник

Как с помощью циркуля и линейки находить корни, квадраты и обратные величины чисел

Время на прочтение
3 мин

Количество просмотров 16K

Представьте, что у вас нет под рукой калькулятора (но есть циркуль и линейка или угольник) и вам нужно посчитать результат в виде отрезка. Задача решается за менее чем 5 простых шагов.

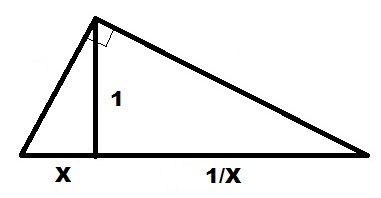
Базовая формула вычисления

Для начала докажем одну формулу, которая нам будет помогать с дальнейшим решением.

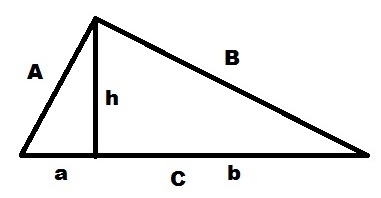
В прямоугольном треугольнике ABC проведем высоту h на сторону C. По теореме Пифагора выводим:

Подставляем всё в первую формулу:

И если раскрыть скобки:

После сокращения получаем:

Вот с помощью этой формулы и будем выводить наши решения.

Единичная мера длины

Так как мы вычисления проводим на плоскости с отрезками, нам необходимо определиться с мерой единичной длины равной 1. Если мы отложим отрезок 1 дециметр, то он так же будет равен 10 сантиметрам, 100 миллиметрам или 4 дюймам. Один отрезок и 4 разных чисел разной меры длины его определяют. Что бы выбрать одну систему счисления длин отрезков, примем за единицу длины какой-то отрезок. Какой – определим по ходу расчетов, и он зафиксирует нужную меру длины.

Циркуль как универсальный инструмент

Циркуль удобно использовать как средство:

отмерить отрезок определенной длины, при этом знать величину этой длины совершенно нет надобности.
прочертить дугу на одинаковом расстоянии от определённой точки.
отложить перпендикуляр к линии через определённую точку. Для этой цели удобнее использовать угольник с прямым углом, чем циркулем чертить 4 дуги.

Вычисление квадрата длины

Для вычисления квадрата величины X используем нашу формулу в виде:

Чертим прямую линию достаточной длины.

Откладываем на ней отрезок единичной длины.

От правого конца единичного отрезка 1 откладываем вверх перпендикуляр длиной X.

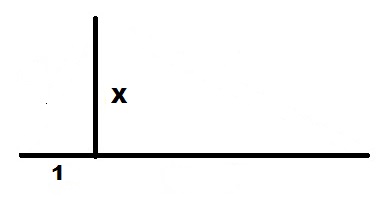
Проводим линию от левого конца единичного отрезка 1 до верхнего конца отрезка X.

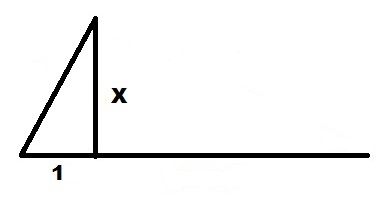
От этого отрезка откладываем перпендикуляр на линию продолжения единичного отрезка 1. Их пересечение и есть правый край квадрата длины. Левый край начинается от точки, где отложена высота.

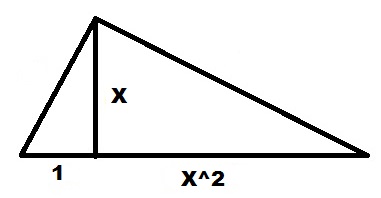
Пример. У вас есть какой-то квадрат, со стороной X, начерченный на плоскости или на земле. Нужно узнать его площадь в попугаях. Одна сторона квадрата длиной X у нас уже есть. На соседней стороне откладываем длину одного попугая (там где 1 находится). Соединяем концы линией, откладываем перпендикуляр, продлеваем отрезок с попугаями до перпендикуляра и получаем решение в квадратных попугаях.

Вычисление квадратного корня длины

Для вычисления квадратного корня величины используем нашу формулу в виде:

Чертим прямую линию достаточной длины.

Откладываем на ней единичный отрезок длины 1.

На продолжении единичного отрезка откладываем отрезок длины X.

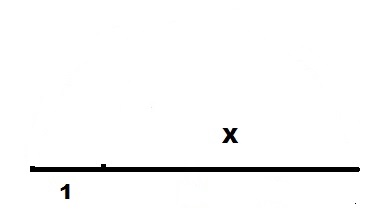
Полученный отрезок 1+X делим пополам с помощью циркуля и получаем точку O. Как это сделать, приводить здесь не буду, это задачка из школьного курса. Обозначим длину найденной половины как R.

Вокруг центра O, циркулем нарисуем дугу радиусом R.

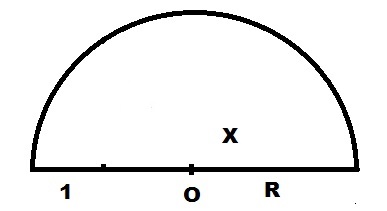
От правого конца отрезка 1 отложим вверх перпендикуляр до пересечения с дугой окружности. Длина этого перпендикуляра и будет равна корню квадратному из длины X.

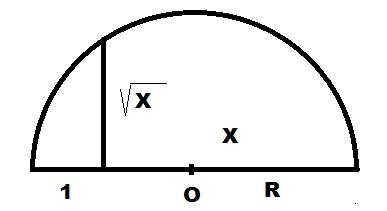
Вычисление обратной величины длины

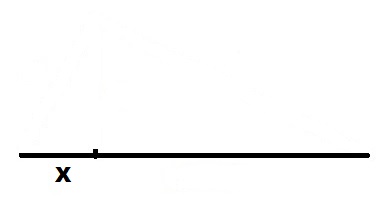
Для вычисления обратной величины длины используем нашу формулу в виде:

Решение очень похоже на нахождение квадрата величины, только a и h меняются местами.

Чертим прямую линию достаточной длины.

Откладываем на ней отрезок длины X.

От правого края отрезка X откладываем вверх перпендикуляр единичной длины 1.

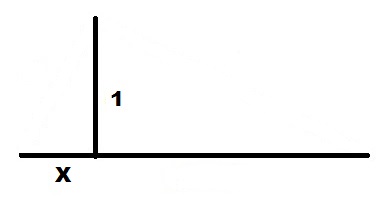
Соединяем концы отрезков линией.

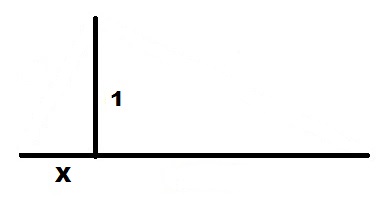
От верхнего конца отрезка X откладываем перпендикуляр к линии продолжения отрезка 1. Полученный отрезок и есть решение.

Выводы

Приведенные выкладки удобны, когда не хочется возиться с цифрами и их арифметическими вычислениями, которые всё равно будут обратно приложены к длинам отрезков.

Если величина X сильно отличается от единичного отрезка 1, ошибка вычисления может быть значительной. Но если применить масштабирование, то ошибку можно значительно уменьшить. Например, при захождении корня длины 20, его можно поделить на 16 (4 раза поделить пополам), а потом ответ умножить на 4 (4 раза отложить полученный отрезок).

Источник

Отбор корней с помощью тригонометрического круга

В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.

«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА

Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.
Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.
Определяем корни, попадающие в эту дугу.
Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.

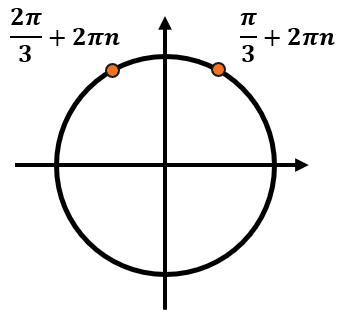
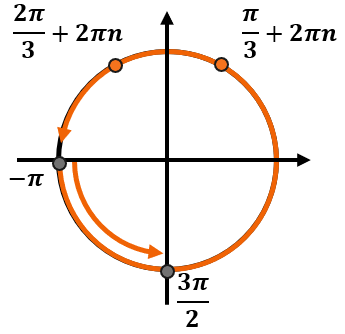
Пример:

Даны корни уравнения:

(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})

(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})

Найдите корни, принадлежащие отрезку (leftlbrack – pi, frac{3pi}{2} rightrbrack).

Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:

При этом мы знаем, что нужные корни должны находиться на промежутке (leftlbrack – pi, frac{3pi}{2} rightrbrack). Этот промежуток занимает больше, чем один оборот. Обозначим его так:

Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.
Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от (- pi) до (frac{3pi}{2}), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:

Запишем ответ.

Ответ: (frac{pi}{3});( frac{2pi}{3}).

Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.

Источник

Отбор корней в тригонометрическом уравнение

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x – cosx = 0

cosx(sqrt(2)cosx – 1) = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx – 1 = 0

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

Обойдем раз против часовой стрелки

Обойдем 2 раза против часовой стрелки

Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

Способы отбора корней в тригонометрических уравнениях

Класс: 10

Автор проекта:
Шелкова Полина,
Класс: 10

Руководитель:
Злобова Людмила Викторовна,
учитель математики

ВВЕДЕНИЕ

Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).

Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.

Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.

I РАЗДЕЛ (теоретический)

Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?

Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
Тригонометрические уравнения включены в КИМы ЕГЭ по математике.

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.

Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.

Задачи:

познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
изучить соответствующую литературу;
научиться решать тригонометрические уравнения;
найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
подготовиться к ЕГЭ по математике.

Приёмы отбора корней тригонометрического уравнения на заданном промежутке.

При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

II РАЗДЕЛ (практический)

Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:

sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]

sinx−(cos 2 x−sin 2 x)=0;

sinx−(1−sin 2 x−sin 2 x)=0;

Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим

Вернемся к замене:

б) Рассмотрим три способа отбора корней, попадающих в отрезок .

1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:

2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни:

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

Нам останется только выбрать корни, которые попали в нужный нам отрезок.

ЗАКЛЮЧЕНИЕ

При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.

СПИСОК ЛИТЕРАТУРЫ

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

Главное — направление, куда мы будем смотреть, а не угол!

Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

Или запомнить такой прием:

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) – ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :

Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
Точки пересечения с окружностью и будут являться корнями уравнения.
Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.

[spoiler title=”источники:”]

http://urok.1sept.ru/articles/687140

http://ik-study.ru/ege_math/trighonomietrichieskiie_uravnieniia

[/spoiler]

Источник

Квадра́тный ко́рень из числа (корень 2-й степени, ) — это число , дающее при возведении в квадрат^[1]. Равносильное определение: квадратный корень из числа — это решение уравнения ${displaystyle x^{2}=a.}$ Операция вычисления значения называется «извлечением квадратного корня» из числа .

Наиболее часто под и подразумеваются вещественные числа, но существуют и обобщения для комплексных чисел и других математических объектов, например матриц и операторов.

Пример для вещественных чисел: потому что ${(pm 3)}^{2}=9.$
У квадратного корня существуют два противоположных, то есть отличающихся знаком, значения (положительное и отрицательное числа), и это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого при всегда неотрицательно (а на положительных — положительно); в примере это число 3.

Содержание

1 Рациональные числа
2 Действительные (вещественные) числа
3 Комплексные числа
4 Квадратный корень как элементарная функция
5 Квадратный корень в элементарной геометрии
6 Квадратный корень в информатике
7 Алгоритмы нахождения квадратного корня
- 7.1 Разложение в ряд Тейлора
- 7.2 Грубая оценка
- 7.3 Геометрическое извлечение квадратного корня
- 7.4 Итерационный аналитический алгоритм
- 7.5 Столбиком
8 Обобщения
9 См. также
10 Примечания
11 Ссылки

Рациональные числа

При рациональных уравнение x^2=a не всегда разрешимо в рациональных числах. Более того, такое уравнение, даже при положительном , разрешимо в рациональных числах тогда и только тогда, когда и числитель и знаменатель числа , представленного в виде несократимой дроби, являются квадратными числами.

Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: $|{sqrt {r}}-p/q|>{frac {1}{Cq^{2}}}$ , где зависит от ^[2]^[3]. Верно и то, что любая периодическая цепная дробь является квадратичной иррациональностью.

Действительные (вещественные) числа

Теорема. Для любого положительного числа существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку.^[4]

Неотрицательный квадратный корень из неотрицательного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала ^[5].

Комплексные числа

Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:

${displaystyle -1=({sqrt {-1}})^{2}={sqrt {(-1)^{2}}}={sqrt {1}}=1}$

(что, конечно, неверно!)

Ошибка возникла из-за того, что квадратный корень является многозначной функцией. В частности, существуют два квадратных корня из 1: -1 и +1.

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если

${displaystyle a=|a|e^{iphi }}$

то (см. Формула Муавра)

${sqrt {a}}={sqrt {|a|}}e^{{i(phi +2pi k)/2}}$

где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом в итоге в ответе получаются два различных результата.

Существует и чисто алгебраическое представление для корня из a+bi ; оба значения корня имеют вид где:

${displaystyle c={sqrt {frac {a+{sqrt {a^{2}+b^{2}}}}{2}}}}$

${displaystyle d=operatorname {sgn}(b){sqrt {frac {-a+{sqrt {a^{2}+b^{2}}}}{2}}}}$

Здесь sgn — функция «знак», а радикалы обозначают обычный арифметический корень из неотрицательного вещественного числа. Формула легко проверяется возведением в квадрат^[6].

Пример: для квадратного корня из формулы дают два значения:

Квадратный корень как элементарная функция

Квадратный корень является элементарной функцией и частным случаем степенной функции ${displaystyle x^{alpha }}$ с . Арифметический квадратный корень является гладким при x>0 , в нуле же он непрерывен справа, но не дифференцируем.^[7]

Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в нуле.

Квадратный корень в элементарной геометрии

Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того.
^[8]

Квадратный корень в информатике

Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).

Алгоритмы нахождения квадратного корня

Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.

Разложение в ряд Тейлора

${displaystyle {sqrt {1+x}}=sum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)(n!)^{2}(4^{n})}}x^{n}=1+textstyle {frac {1}{2}}x-{frac {1}{8}}x^{2}+{frac {1}{16}}x^{3}-{frac {5}{128}}x^{4}+dots ,}$

при

Грубая оценка

Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:

Если D нечётно, D = 2n + 1, тогда используем ${sqrt {S}}approx 2cdot 10^{n}.$

Если D чётно, D = 2n + 2, тогда используем ${sqrt {S}}approx 6cdot 10^{n}.$

Два и шесть используются потому, что и

При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку $2^{{leftlfloor D/2rightrfloor }}$ (здесь D это число двоичных цифр).

Геометрическое извлечение квадратного корня

В частности, если , а , то
^[9]

Итерационный аналитический алгоритм

Последовательные приближения рассчитываются по формуле:
${displaystyle {begin{cases}x_{0}=a\x_{n+1}={frac {1}{2}}left(x_{n}+{frac {a}{x_{n}}}right)end{cases}}}$
тогда $lim _{{nto infty }}x_{n}={sqrt {a}}$

Этот метод сходится очень быстро. Например, если для взять начальное приближение ${displaystyle x_{0}=2,}$ то получим:

${displaystyle x_{1}={frac {9}{4}}=2{,}25; x_{2}={frac {161}{72}}=2{,}23611;;x_{3}={frac {51841}{23184}}=2{,}2360679779.}$

В заключительном значении верны все цифры, кроме последней.

Столбиком

Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.

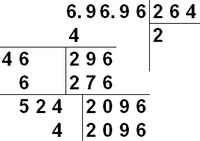
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа N с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234,567 можно представить, как 03 12 34, 56 70. В отличие от деления снос производится такими группами по 2 цифры.

Записать число N (в примере — 69696) на листке.
Найти , квадрат которого меньше или равен группе старших разрядов числа N (старшая группа — самая левая не равная нулю), а квадрат больше группы старших разрядов числа. Записать найденное справа от N (это очередная цифра искомого корня). (На первом шаге примера $a^{2}=2^{2}=2cdot 2=4<6$ , а $(a+1)^{2}=3^{2}=3cdot 3=9>6$ ).
Записать квадрат под старшей группой разрядов. Провести вычитание из старшей группы разрядов N выписанного квадрата числа и записать результат вычитания под ними.
Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число равное уже найденным цифрам результата (мы их выписываем справа от N) умноженное на 20. Назовём это число . (На первом шаге примера это число просто есть , на втором ).
Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа N справа от результата вычитания. Назовем число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число , на втором ). Если сносится первая группа после десятичной точки числа N, то нужно поставить точку справа от уже найденных цифр искомого корня.
Теперь нужно найти такое , что меньше или равно , но больше, чем . Записать найденное справа от N, как очередную цифру искомого корня. Вполне возможно, что окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как , но ) Если число найденных цифр уже удовлетворяет искомой точности прекращаем процесс вычисления.
Записать число под . Провести вычитание столбиком числа из и записать результат вычитания под ними. Перейти к шагу 4.

Наглядное описание алгоритма:

Обобщения

Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц^[10], функций^[11], операторов^[12] и т. п. В качестве операции circ при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.

В алгебре применяется следующее формальное определение: Пусть — группоид и ain G . Элемент xin G называется квадратным корнем из если .

См. также

Быстрый инверсный квадратный корень
Вложенные радикалы
День квадратного корня
Итерационная формула Герона
Квадратное уравнение
Корень (математика)
Кубический корень
Теорема Абеля — Руффини

Примечания

↑ Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
↑ Теорема Лиувилля о приближении алгебраических чисел
↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1975 г., п. 1.2.1
↑ Cooke, Roger. Classical algebra: its nature, origins, and uses. — John Wiley and Sons, 2008. — P. 59. — ISBN 0-470-25952-3.
↑ Фихтенгольц, гл. 2, § 1
↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148
↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.

Ссылки

Алгоритмы вычисления квадратного корня
A geometric view of the square root algorithm
Соловьев Ю., Старый алгоритм

Источник

Начальная оценка[править | править код]

Десятичная оценка[править | править код]

Скалярные оценки[править | править код]

Линейная оценка[править | править код]

Гиперболическая оценка[править | править код]

Арифметическая оценка[править | править код]

Двоичная оценка[править | править код]

Вавилонский метод[править | править код]

Пример[править | править код]

Сходимость[править | править код]

Сходимость в худшем случае[править | править код]

Метод Бакхшали[править | править код]

Пример[править | править код]

Цифра за цифрой[править | править код]

Основной принцип[править | править код]

Десятичная система счисления[править | править код]

Примеры[править | править код]

Двоичная система счисления[править | править код]

Экспоненциальное тождество[править | править код]

Итеративный метод с двумя переменными[править | править код]

Итеративные методы вычисления обратного к квадратному корню числа[править | править код]

Алгоритм Гольдшмидта[править | править код]

Ряды Тейлора[править | править код]

Разложение в цепную дробь[править | править код]

Метод последовательности Люка[править | править код]

Аппроксимации, зависящие от представления в виде числа с плавающей запятой[править | править код]

Обратное значение квадратного корня[править | править код]

Корень из отрицательного или комплексного числа[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

СсылкиWeisstein, Eric W. Square root algorithms (англ.) на сайте Wolfram MathWorld.[править | править код]

Как с помощью циркуля и линейки находить корни, квадраты и обратные величины чисел

Базовая формула вычисления

Единичная мера длины

Циркуль как универсальный инструмент

Вычисление квадрата длины

Вычисление квадратного корня длины

Вычисление обратной величины длины

Выводы

Отбор корней с помощью тригонометрического круга

Отбор корней в тригонометрическом уравнение

Способы отбора корней в тригонометрических уравнениях

Автор проекта: Шелкова Полина, Класс: 10

ВВЕДЕНИЕ

I РАЗДЕЛ (теоретический)

II РАЗДЕЛ (практический)

ЗАКЛЮЧЕНИЕ

Тригонометрические уравнения

Содержание

Рациональные числа

Действительные (вещественные) числа

Комплексные числа

Квадратный корень как элементарная функция

Квадратный корень в элементарной геометрии

Квадратный корень в информатике

Алгоритмы нахождения квадратного корня

Разложение в ряд Тейлора

Грубая оценка

Геометрическое извлечение квадратного корня

Итерационный аналитический алгоритм

Столбиком

Обобщения

См. также

Примечания

Ссылки

Вам также может понравиться

Сталкер тайные тропы 2 как найти сверхпроводник

Как найти комнату для студента

Как найти человека по imei телефона

Добавить комментарий Отменить ответ

Автор проекта:
Шелкова Полина,
Класс: 10