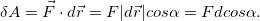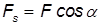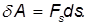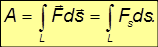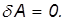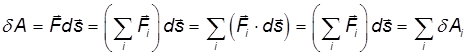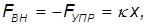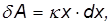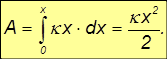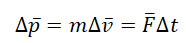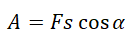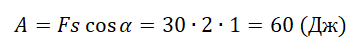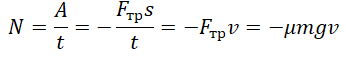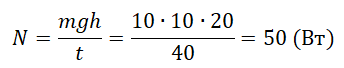Как геометрически найти работу

Механическая работа

О чем эта статья:

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения [°]

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

• чтобы на тело действовала сила,
• чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Е_п = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

За счет чего происходит процесс?

Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости [°]

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

Сила вязкого трения.

Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Работа силы через векторы

4.1. Работа силы

Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).

Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

Рис 4.1. Элементарная работа

Элементарная работа силы 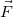равна скалярному произведению вектора силы на вектор перемещения её точки приложения

Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина

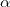
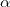
— это проекция силы F на направление перемещения. Следовательно,

Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:

При перемещении вдоль оси x работу графически можно представить как площадь под кривой F_x(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.

Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = F_x(x)

Если перемещение ортогонально силе, то = 0 и работа равна нулю:

Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.

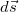
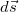
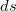
Если на тело действует несколько сил, то

то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.

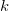
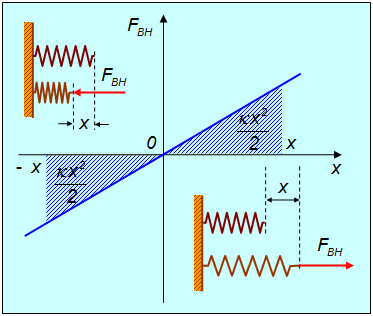
Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью . Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука

где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).

Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины

Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид

так что для полной работы упругой деформации пружины получаем

Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.

Механическая работа

О чем эта статья:

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения []

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

• чтобы на тело действовала сила,
• чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Е_п = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

1. За счет чего происходит процесс?
2. Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости []

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

1. Выталкивающая сила.
2. Сила вязкого трения.
3. Сила тяжести.
4. Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Механическая работа и мощность

теория по физике 🧲 законы сохранения

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

Важно!

Механическая работа совершается, если:

1. На тело действует сила.
2. Под действием этой силы тело перемещается.
3. Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Модуль силы тяжести: F_тяж = mg

Работа силы тяжести: A = mgs cosα

Модуль силы трения скольжения: F_тр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Модуль силы упругости: F_упр = kx

Работа силы упругости:

Работа силы тяжести

Работа силы трения скольжения

Работа силы упругости

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

1. Если α = 0 о , то cosα = 1.
2. Если 0 о o , то cosα > 0.
3. Если α = 90 о , то cosα = 0.
4. Если 90 о o , то cosα о , то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

F_т — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

• Работа затраченная — полная работа силы, совершенной над телом (или телом).
• Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
• Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

Неподвижный блок, рычаг

Наклонная плоскость

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

Механическая работа и мощность

теория по физике 🧲 законы сохранения

Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:

В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.

Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).

Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:

Важно!

Механическая работа совершается, если:

1. На тело действует сила.
2. Под действием этой силы тело перемещается.
3. Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).

Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.

Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.

Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:

Работа различных сил

Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.

Модуль силы тяжести: F_тяж = mg

Работа силы тяжести: A = mgs cosα

Модуль силы трения скольжения: F_тр = μN = μmg

Работа силы трения скольжения: A = μmgs cosα

Модуль силы упругости: F_упр = kx

Работа силы упругости:

Работа силы тяжести

Работа силы трения скольжения

Работа силы упругости

Работа силы упругости

Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:

Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя

Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.

A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)

Знак работы силы

Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:

1. Если α = 0 о , то cosα = 1.
2. Если 0 о o , то cosα > 0.
3. Если α = 90 о , то cosα = 0.
4. Если 90 о o , то cosα о , то cosα = –1.

Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.

Геометрический смысл работы

Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

Мощность

Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.

Мощность при равномерном прямолинейном движении тела

Работа при равномерном прямолинейном движении определяется формулой:

F_т — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:

Мощность при равномерном подъеме груза

Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:

Мгновенная мощность при неравномерном движении

Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:

Мощность силы трения при равномерном движении по горизонтали

Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180 о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:

Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?

Коэффициент полезного действия

Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.

• Работа затраченная — полная работа силы, совершенной над телом (или телом).
• Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
• Коэффициент полезного действия(КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.

КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:

Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:

Устройство

Работа полезная и полная

Неподвижный блок, рычаг

Наклонная плоскость

l — совершенный путь (длина наклонной плоскости).

Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.

В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/rabota-sily-cherez-vektory

[/spoiler]

Многие задачи на совместную работу, решаемые в школьном курсе математики, имеют практическое содержание. Геометрический метод решения таких задач позволяет провести параллель с физикой, где использование системы координат достаточно часто применяется при решении физических задач.

Графический способ решения задач, чтение графиков, а так же умение дать ответ на поставленный вопрос используя только графические данные – неотъемлемая часть знаний, необходимых для успешной сдачи ЕГЭ и ГИА и поступления в ВУЗ.

Кроме того, в ходе освоения графического метода решения текстовых задач формируются практические навыки, развиваются представления о роли вычислений в человеческой практике, развивается вычислительная культура. Благодаря текстовым задачам легко увидеть практическое применение своих знаний в жизни. Умение решать текстовые задачи позволит помочь, например, при ремонте квартиры, при расчетах необходимых затрат или времени. Все вышеперечисленное в свою очередь развивает познавательный интерес к математике и готовит к самостоятельности мышления.     

Рассмотрим несколько текстовых задач на совместную работу и решим их с использованием геометрического метода.

Задача 1.

Двое рабочих, выполняя некоторое задание вместе, могли бы справиться с ним за 12 дней. Если сначала будет работать только один из них, а когда он выполнит половину всей работы, его сменит второй рабочий, то  все задание будет выполнено за 25 дней. За какой срок работая в одиночку второй рабочий сможет выполнить все задание?

Решение.

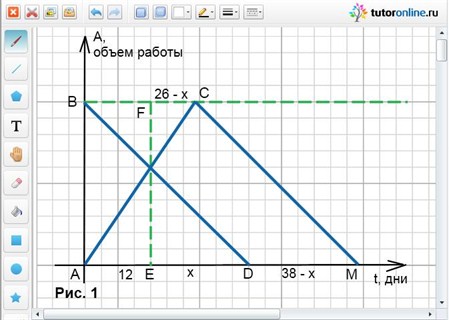
Рассмотрим рис. 1. АС и BD – графики зависимости выполненного объема работы от времени, затраченного первым и вторым рабочими соответственно.

Время совместной работы – 12 дней, на рисунке имеем: BF = AE = 12.

АМ – время, за которое каждый из рабочих выполнит всю работу (второй начинает работать сразу же после того, как первый заканчивает). Сказано, что рабочим необходимо 25 дней, чтобы выполнить по половине всей работы, тогда

АМ = 2 · 25 = 50 дней. Пусть ЕD = x, тогда

DM = 50 – 12 – x = 38 – x;

FC = BC – BF = (38 – x) – 12 = 26 – x.

Рассмотрим пары подобных по двум углам треугольников:

ΔBFO подобен ΔOED, тогда BF/ED = FO/OE; 12/x = FO/OE.

ΔFOC подобен ΔEOA, тогда FC/AE = FO/OE; (26 – x)/12 = FO/OE.

Таким образом, 12/x = (26 – x)/12. Перепишем: (26 – x)х = 12 · 12;

Имеем квадратное уравнение

х² – 26х + 144 = 0, корни которого х = 18 или х = 8.

Очевидно, что х = 18 не подходит по смыслу задачи, так как 12 + 18 = 30 > 25, значит, х = 8, тогда

AD = 12 + 8 = 20 (дней); ВС = 12 + 26 – х = 12 + 26 – 8 = 30 (дней).

Ответ: 30 дней.

Задача 2.

Двое рабочих, работая независимо один от другого, оклеили обоями за 7 дней несколько комнат, причем второй рабочий приступил к работе на 1,5 дня позже первого. Дни, которые понадобились для оклейки 7 комнат, считаются с момента выхода на работу первого рабочего. Если бы эта работа выполнялась каждым рабочим в отдельности, то первому рабочему для ее выполнения понадобилось бы на 3 дня больше, чем второму. За сколько дней второй рабочий выполнил бы всю необходимую работу в одиночку?  

Решение.

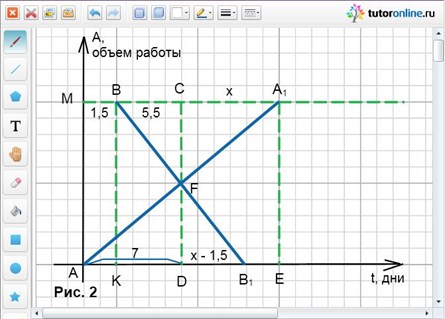
Рассмотрим рис. 2. АА1 и BВ1 – графики зависимости выполненного объема работы от времени, затраченного первым и вторым рабочими соответственно.

Имеем, что ВМ = 1,5 дня,  AD = 7 дней. Время выполнения всей работы каждым рабочим в отдельности – это АЕ и КВ1, причем AE = КВ1 + 3;

По условию задачи В1Е = АЕ – КВ1 = АЕ – 1,5 – (АЕ – 3) = 1,5.

Пусть СА1 = x, тогда DB1 = x – 1,5.

Пользуемся подобием треугольников:

ΔBСF подобен ΔВ1DF (по двум углам), тогда

BC/DB1 = CF/FD; 5,5/(x – 1,5) = CF/FD.

ΔA1CF подобен ΔADF (по двум углам), тогда

A1C/AD = CF/FC; x/7 = CF/FD.

Таким образом, 5,5/(x – 1,5) = x/7.

Перепишем:

х² – 1,5х = 38,5;

2х² – 3х – 77 = 0;

х = 7 или х = -5,5.

Очевидно, что по смыслу задачи х = 7 дней.

Таким образом, КВ1 = АВ1 – АК = 7 + х – 1,5 – 1,5 = 7 + 7 – 3 = 11 дней.

Ответ: 11 дней.

Задача 3.

Чан наполняется водой при помощи двух кранов А и В. Наполнение чана только с помощью крана А длится на 22 минуты дольше, чем наполнение через кран В. Если же оба крана открыть одновременно, то чан наполнится водой за 1 час. За какое время может наполнить водой чан только кран В?

Решение.

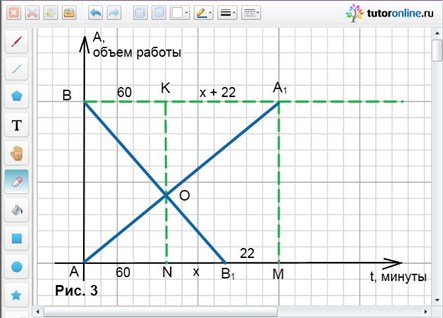
Рассмотрим рис. 3. На нем АА1 и BВ1 – графики зависимости выполненного объема работы от времени наполнения чанов водой кранами А и В соответственно.

По условию задачи ВК = АN = 1 час = 60 минут. В1М = 22 минуты.

Пусть NB1 = x, тогда KA1 = x + 22.

Используем подобие треугольников:

ΔBКО подобен ΔВ1NO, тогда BK/NB1 = KO/ON; 60/x = KO/ON.

ΔKOA1 подобен ΔNOA, тогда KA1/AN = KO/ON; (x + 22)/60 = KO/ON.

Таким образом, имеем пропорцию 60/x = (x + 22)/60.

Перепишем в виде квадратного уравнения:

х² + 22х – 3600 = 0;

х = 50 или х = -72.

По смыслу задачи х = 50 минут.

Таким образом, АВ1 = AN + NВ1 = 60 + 50 = 110 (минут).

Ответ: 110 минут.

Мы рассмотрели решение задач на совместную работу с помощью геометрического способа. Такие навыки решения задач могут пригодиться не только в математике, но и в физике, где графические подходы к решению задач практикуются достаточно часто.

 Остались вопросы? Не знаете, как решать задачи на работу?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Если человек занимается не подходящим ему делом, то это не просто накладывает на него отпечаток, но и загоняет его в рутину. Для того чтобы избежать подобных ситуаций вам стоит пройти психогеометрический тест 5 фигур. Он поможет вам найти свой путь в жизни и расскажет чем вам стоит заниматься.

Этот геометрический тест не говорит вам бросать основную работу и не намекает, что вы выбрали не ту профессию. В данном случае вы сможете найти отдушину, которой стоит посвящать время. Тогда ваша жизнь превратиться в сказку!

Как проводить психогеометрический тест?

Для самостоятельного прохождения теста вам потребуется придерживаться некоторых рекомендаций:

• Тест геометрические фигуры не требует особой подготовки, но вам всё же стоит провести 2-3 минуты в спокойствии и расслабиться.
• После, посмотрите на представленную картинку.
• Долго не раздумывайте и очень быстро принимайте решение.
• По выбранной фигуре прочитайте расшифровку ниже.

Воспрещается читать ответы перед проведением проверки. Если вы поменяете порядок проведения, то вы можете провалить тест.

Ответы на тест с геометрическими фигурами

Читаем расшифровку вашего выбора:

• Круг – вы очень добродушная личность, которая всегда стремиться посеять светлое семечко в этом мире. Вот почему вам стоит работать с людьми, и помогать решать их проблемы.

Это ваше призвание! Вы так же можете посвятить себя благотворительности или стать волонтёром. Вам это воздастся в тройном размере.

• Квадрат – вы очень пунктуальны и ваша работа всегда структурирована. Если вы работаете с расчётами или точными науками, то вам повезло.

Вам начертано судьбой раскладывать всё по полочкам. Если вам нужно расслабляющее занятие, то для вас это тренировка ума: проходите квесты, решайте головоломки или собирайте пазлы.

• Треугольник – вы творческая личность и вам нужен простор для мышления. Поэтому вы можете работать в любой отрасли, где требуется креативное мышление.

В качестве хобби выберите для себя что-нибудь: моделирование одежды, пение, игра на каком-либо инструменте или займитесь оформлением комнаты.

• «Х» – вам повезло! Вы разносторонняя личность, которая интересуется всем, чем только пожелает. Смело выбирайте то, что вам нравится. Однако у вас есть один минус, который вам постоянно мешает.

Вы ленивы! Причём возможно эта лень от большого ума, но всё же. Вы не доводите свои дела до конца и в этом ваша проблема.

Данный геометрический психологический тест поможет вам найти подходящее хобби. Вы обязательно прислушайтесь к советам и попробуйте окунуться в неизведанный вам мир. Тогда перед вами откроются новые границы.

Поделись этим интересным тестом с друзьями, пусть они тоже будут в курсе!

OBRAZOVALKA.COM

OBRAZOVALKA.COM – образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .

Наша доска вопросов и ответов в первую очередь ориентирована на школьников и студентов из России и стран СНГ, а также носителей русского языка в других странах.

Для посетителей из стран СНГ есть возможно задать вопросы по таким предметам как Украинский язык, Белорусский язык, Казакхский язык, Узбекский язык, Кыргызский язык.

На вопросы могут отвечать также любые пользователи, в том числе и педагоги.

---

Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.

В условиях собеседования важна оперативность в получении информации о соискателе. Результаты психологического тестирования, как правило, второстепенны по сравнению с профессиональными навыками и опытом работы, но они могут стать фактической основой для обсуждения личностных и деловых качеств кандидата, а также сориентируют, на что обратить внимание в ходе дальнейшей беседы.

Простой и достаточно популярный психогеометрический тест направлен на диагностику типа личности. Точность результатов данного метода достигает 85%. Перед соискателем кладется лист с изображением 5 геометрических фигур (квадрата, прямоугольника, треугольника, круга и зигзага).Соискателю предлагается выбрать фигуры в порядке привлекательности. То есть первая фигура — та, которая нравится больше всего и так далее.

Наибольшее значение имеет то, какую из фигур респондент расположит первой — это так называемая субъективная форма человека, которая позволяет определить доминирующие черты характера и особенности поведения. Последняя фигура в ряду указывает на форму человека, взаимодействие с которым может вызывать конфликты и непонимание.

Квадрат

Татьяна Маркова, HR-консультант: «Психогеометрия сейчас популярна во многих странах. В своей работе я часто пользуюсь такой методикой. В каждом человеке всегда присутствует определенная пропорция свойств этих фигур. Но посмотрев на первую и последнюю фигуру, можно говорить как о доминантных свойствах личности, так и тех, которые находятся в меньшинстве».

Те, кто поставил квадрат на первое место, пунктуальны, точны, аккуратны и внимательны к деталям. Их идеал — распланированная, предсказуемая жизнь. Они постоянно «упорядочивают», организуют людей и вещи вокруг себя. «Квадраты» могут стать хорошими специалистами — техниками, отличными администраторами, но редко бывают хорошими менеджерами. Чрезмерное пристрастие к деталям, потребность в уточняющей информации для принятия решений лишает Квадрата оперативности. Кроме того, рациональность, эмоциональная сухость, консерватизм в оценках мешают Квадратам устанавливать контакты.

Психологические свойства Квадрата

Положительные	Отрицательные
Организованный	Педант, дотошный, мелочный
Внимателен к деталям	Из-за деревьев не видит леса
Аналитичный	Холодный, отчужденный, сухой
Твердый в решениях	Консервативный, сопротивляющийся инновациям
Терпеливый	Выжидающий, затягивающий решения

Треугольник

Таких людей характеризует лидерство и способность концентрироваться на главной цели, вникнуть в суть проблемы. Потребность быть правым и управлять положением дел, решать не только за себя, но и за других, делает Треугольника личностью, постоянно соперничающей, конкурирующей с другими.

Психологические свойства Треугольника

Положительные	Отрицательные
Лидер, принимающий ответственность на себя	Эгоцентричный, эгоистичный
Решительный	Категоричный, не терпящий возражений
Сконцентрированный на цели	Безразличный ко всему остальному, пока цель не будет достигнута
Уверенный в себе	Самонадеянный
Честолюбивый	Ориентированный на статус, карьеру

Прямоугольник

Переходное состояние личности, что отражается в замешательстве и неопределенности в отношении себя на данный момент времени. Наиболее характерные черты Прямоугольников — непоследовательность и непредсказуемость поступков в течение переходного периода. В то же время в данный период они открыты для новых идей, ценностей, способов мышления и жизни.

Психологические свойства Прямоугольника

Положительные	Отрицательные
Возбужденный	Напряженный, в состоянии замешательства
Ищущий	Непоследовательный, непостоянный
Любознательный	Легковерный, внушаемый
Чувствительный	Эмоционально неустойчивый
Неамбициозный	Низкая самооценка

Круг

Тот, кто уверенно выбирает круг в качестве своей основной формы, искренне заинтересован, прежде всего, в хороших межличностных отношениях. Высшая ценность для Круга — люди, их благополучие. Он чаще всего служит тем «клеем», который скрепляет рабочий коллектив и стабилизирует группу. Они обладают высокой чувствительностью, развитой эмпатией — способностью сопереживать, сочувствовать. Однако они, как правило, слабые менеджеры и руководители в сфере бизнеса. Они пытаются сохранить мир и ради этого иногда избегают занимать «твердую» позицию и принимать непопулярные решения, боясь вступать в межличностный конфликт.

Психологические свойства Круга

Положительные	Отрицательные
Дружелюбный, доброжелательный	Мягкотелый, нетребовательный, уступающий
Сочувствующий	Болтливый, любит посплетничать
Способен убеждать и мотивировать других	Играет на чувствах других
Спокойный, внутренне не напряженный	Ленивый, слабая концентрация, низкая мотивация достижения
Бесконфликтный, стабилизирующий	Слабый «политик»

Зигзаг

Эта фигура символизирует креативность, творчество. Зигзаги просто не могут продуктивно трудиться в хорошо структурированных ситуациях. Их раздражают четкие вертикальные и горизонтальные связи и строго фиксированные обязанности. В работе им требуется независимость от других и высокий уровень стимуляции на рабочем месте. Тогда Зигзаг оживает и начинает выполнять свое основное назначение — генерировать новые идеи и методы работы.

Психологические свойства Зигзага

Положительные	Отрицательные
Креативность, творческий подход к жизни	Неорганизованность, разбросанность
Концептуальность, теоретическая установка	Непрактичность
Интуитивность	Нелогичность, непоследовательность
Остроумие	Эксцентричность
Экспрессивность, прямота	Несдержанность, непосредственность

Безусловно, ни одна из фигур не является лучшей или худшей. Вопрос лишь в том, насколько, по мнению работодателя, для данной конкретной должности важны те или иные личностные качества претендента. И если лучшие психологи получаются из Кругов, то Треугольник вполне может стать отличным руководителем регионального развития.

Елена Никифорова

Разместить резюме
Добавить вакансию