Как герон нашел формула герона

Фо́рмула Герона — формула для вычисления площади треугольника по длинам его сторон a,b,c :

{displaystyle S={sqrt {p(p-a)(p-b)(p-c)}}}

где — полупериметр треугольника: ${displaystyle p={tfrac {1}{2}}cdot (a+b+c)}$ .

Формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми, такие треугольники носят название героновых, простейшим героновым треугольником является египетский треугольник.

Доказательство 1 (тригонометрическое):

Доказательство 2 (на основе теоремы Пифагора):

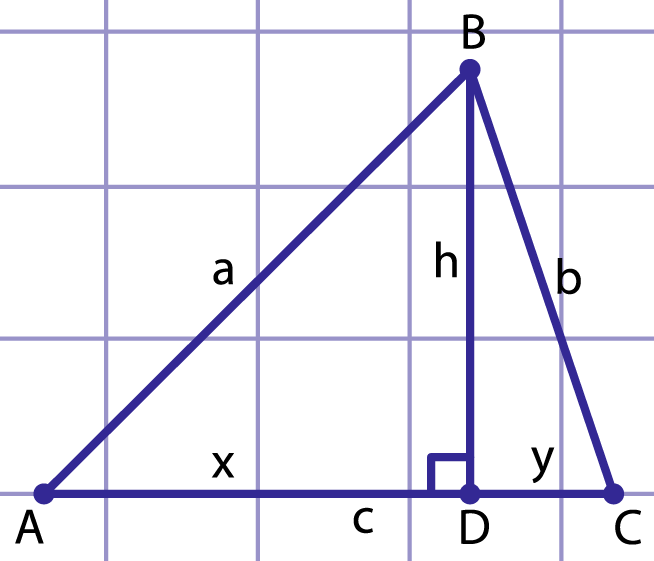
Треугольник со сторонами a, b, c и высотой

h, разделяющей основание

c на

d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a² = h² + (c − d)² и b² = h² + d² — см. рисунок справа. Вычитая из первого равенства второе, получаем a² − b² = c² − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

${displaystyle d={frac {-a^{2}+b^{2}+c^{2}}{2c}}}$

Для высоты h у нас было равенство h² = b² − d², в которое можно подставить полученное выражение для d и применить формулы для квадратов:

${displaystyle {begin{aligned}h^{2}&=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}={frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\&={frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\end{aligned}}}$

Замечая, что , , , , получаем:

${displaystyle {begin{aligned}h^{2}&={frac {2(p-a)cdot 2pcdot 2(p-c)cdot 2(p-b)}{4c^{2}}}={frac {4p(p-a)(p-b)(p-c)}{c^{2}}}end{aligned}}}$

Используя основное равенство для площади треугольника ${displaystyle S={frac {ch}{2}}}$ и подставляя в него полученное выражение для h, в итоге имеем:

${displaystyle {begin{aligned}S={sqrt {{frac {c^{2}}{4}}cdot {frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={sqrt {p(p-a)(p-b)(p-c)}}end{aligned}}}$

ч.т.д.

Вариации и обобщения[править | править код]

Формулу Герона можно записать с помощью определителя в виде^[1]:

$-16S^{2}={begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}={begin{vmatrix}a&b&c&0\b&a&0&c\c&0&a&b\0&c&b&aend{vmatrix}}$

Первый определитель последней формулы является частным случаем определителя Кэли — Менгера^[en] для вычисления гиперобъёма симплекса.

через длины высот $h_{a}$

, $h_{b}$

и $h_{c}$

и полусумму их обратных величин $H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2$

^[3]:

$S^{-1}=4{sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}$

;

через углы треугольника alpha

, полусумму их синусов

{displaystyle s=(sin alpha +sin beta +sin gamma )/2}

и диаметр описанной окружности ${displaystyle D={tfrac {a}{sin alpha }}={tfrac {b}{sin beta }}={tfrac {c}{sin gamma }}}$

^[4]:

$S=D^{2}{sqrt {s(s-sin alpha )(s-sin beta )(s-sin gamma )}}.$

Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты:

,

где $p={frac {a+b+c+d}{2}}$

— полупериметр четырёхугольника; в данном случае треугольник оказывается предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Та же формула Брахмагупты через определитель^[5]:

$S={frac {1}{4}}{sqrt {-{begin{vmatrix}a&b&c&-d\b&a&-d&c\c&-d&a&b\-d&c&b&aend{vmatrix}}}}$

где:

${displaystyle {begin{aligned}a&={sqrt {xYZ}}\b&={sqrt {yZX}}\c&={sqrt {zXY}}\d&={sqrt {xyz}}\X&=(w-U+v),(U+v+w)\x&=(U-v+w),(v-w+U)\Y&=(u-V+w),(V+w+u)\y&=(V-w+u),(w-u+V)\Z&=(v-W+u),(W+u+v)\z&=(W-u+v),(u-v+W)end{aligned}}}$

где $theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}}$

— полупериметр.

Примечания[править | править код]

↑ Weisstein, Eric W. Heron’s Formula. Архивная копия от 5 сентября 2015 на Wayback Machine From MathWorld–A Wolfram Web Resource.
↑ Benyi, Arpad, “A Heron-type formula for the triangle, « Mathematical Gazette» 87, July 2003, 324—326.
↑ Mitchell, Douglas W., “A Heron-type formula for the reciprocal area of a triangle, ” Mathematical Gazette 89, November 2005, 494.
↑ Mitchell, Douglas W., “A Heron-type area formula in terms of sines, ” Mathematical Gazette 93, March 2009, 108—109.
↑ Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1] Архивная копия от 27 июня 2013 на Wayback Machine, pp. 16-17.
↑ Маркелов С. Формула для объёма тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132

Литература[править | править код]

§ 258 в А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
Николаев Н. О площади треугольника // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора

Источник

Формула Герона

Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.

Формулировка теоремы Герона

Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.

Формула и доказательство

Формула Герона выглядит следующим образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(S;=;sqrt{pleft(p-aright)left(p-bright)left(p-cright)})

где S – это площадь треугольника; a, b, c – это стороны треугольника; p – это полупериметр треугольника.

Чтобы вычислять полупериметр, нужно пользоваться формулой:

(p;=;frac{a+b+c}2)

Приведем доказательство.

Для этого рассмотрим треугольник ABC.

CH – высота треугольника.

Тогда (c=x+y).

По теореме Пифагора из треугольников ACH и BCH получаем:

(h^2=b^2-x^2=a^2-y^2)

Из этого:

(y^2-x^2=a^2-b^2)

((y-x)(y+x)=a^2-b^2)

(x+y=c)

Соответственно:

((y-x)c=a^2-b^2) и (y-x=frac1c (a^2-b^2))

Если сложить последнее равенство с (y+x=c), то получается

(y;=;frac{c^2+a^2-b^2}{2c})

Треугольник

Найдем высоту треугольника.

(h^2;=;a^2-y^2=left(a-yright)left(a+yright)=left(a-frac{c^2+a^2-b^2}{2c}right)left(a+frac{c^2+a^2-b^2}{2c}right)=frac{2ac-c^2-a^2+b^2}{2c}timesfrac{2ac+c^2+a^2-b^2}{2c}=frac{b^2-left(a-cright)^2}{2c}timesfrac{left(a+cright)^2-b^2}{2c}=frac{left(b-a+cright)timesleft(b+a-cright)}{2c}timesfrac{left(a+c-bright)timesleft(a+c+bright)}{2c})

Так как (p=frac12left(a+b+cright)), то ( b+c=2p-a),( a+b=2p-c), (a+c=2p-b), (a+b+c=2p).

С помощью этих равенств найдем высоту.

(h^2=frac{left(2p-2aright)left(2p-2cright)left(2p-2bright)2p}{4c^2}=frac{4pleft(p-aright)left(p-cright)left(p-bright)}{c^2})

А так как (S=frac12ch), то теорема доказана.

Для каких треугольников действует теорема

Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.

Примеры решения задач

Задача 1

Рассчитать площадь треугольника, если a=6, b=8, c=6.

Решение

(p=frac{6+8+6}2=10)

Тогда площадь треугольника равна:

(S=10sqrt{left(10-6right)left(10-8right)left(10-6right)}=320)

Ответ: 320 см².

Задача 2

Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.

Решение

Диагонали AC и BD пересекаются в точке O.

Если AD = 51, AC = 40 и BD = 74, то AO = 20, OD = 37.

По формуле Герона:

(S_{ABCD} = 4S_{AOD} = sqrt{54left(54-51right)left(54-37right)left(54-20right)}=1224)

Ответ: 1224 см².

Задача 3

В треугольнике ABC три стороны: AB = 26, BC = 30 и AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.

Решение

Задача 3

BP и BQ – высота и биссектриса треугольника.

По формуле Герона:

(S=sqrt{42left(42-30right)left(42-28right)left(42-26right)}=336)

(S = ½ AC·BP)

Поэтому (BP =frac{2S}{AC}=frac{2times336}{28}=24).

По свойству биссектрисы треугольника:

(frac{AQ}{QC}=frac{AB}{BC}=frac{26}{30}=frac{13}{15})

Соответственно (AQ=frac{13}{28}AC = 13).

По теореме Пифагора из треугольника APB получаем:

(AP=sqrt{AP^2-BP^2}=sqrt{26^2-24^2}=sqrt{2times50}=10)

Следовательно, (PQ = AQ – AP = 13 – 10 = 3)

(S_{BPQ} = ½ PQ·BP = frac{3times24}2=36)

Ответ: 36 см².

Источник

From Wikipedia, the free encyclopedia

This article is about calculating the area of a triangle. For calculating a square root, see Heron’s method.

A triangle with sides a, b, and c

In geometry, Heron’s formula (or Hero’s formula) gives the area of a triangle in terms of the three side lengths a, b, c. If ${textstyle s={tfrac {1}{2}}(a+b+c)}$ is the semiperimeter of the triangle, the area A is,^[1]

It is named after first-century engineer Heron of Alexandria (or Hero) who proved it in his work Metrica, though it was probably known centuries earlier.

Example[edit]

Let △ABC be the triangle with sides a = 4, b = 13 and c = 15.
This triangle’s semiperimeter is

${displaystyle s={frac {a+b+c}{2}}={frac {4+13+15}{2}}=16}$

and so the area is

$begin{align} A &= sqrt{sleft(s-aright)left(s-bright)left(s-cright)} = sqrt{16 cdot (16-4) cdot (16-13) cdot (16-15)}\ &= sqrt{16 cdot 12 cdot 3 cdot 1} = sqrt{576} = 24. end{align}$

In this example, the side lengths and area are integers, making it a Heronian triangle. However, Heron’s formula works equally well in cases where one or more of the side lengths are not integers.

Alternate expressions[edit]

Heron’s formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways,

${displaystyle {begin{aligned}A&={tfrac {1}{4}}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\[6mu]&={tfrac {1}{4}}{sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}\[6mu]&={tfrac {1}{4}}{sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}\[6mu]&={tfrac {1}{4}}{sqrt {4(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{2}+b^{2}+c^{2})^{2}}}\[6mu]&={tfrac {1}{4}}{sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}.end{aligned}}}$

After expansion, the expression under the square root is a quadratic polynomial of the squared side lengths a², b², c².

The same relation can be expressed using the Cayley–Menger determinant,

${displaystyle -16A^{2}={begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}.}$

History[edit]

The formula is credited to Heron (or Hero) of Alexandria (fl. 60 AD),^[2] and a proof can be found in his book Metrica. Mathematical historian Thomas Heath suggested that Archimedes knew the formula over two centuries earlier,^[3] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.^[4]

A formula equivalent to Heron’s, namely,

${displaystyle A={frac {1}{2}}{sqrt {a^{2}c^{2}-left({frac {a^{2}+c^{2}-b^{2}}{2}}right)^{2}}}}$

was discovered by the Chinese. It was published in Mathematical Treatise in Nine Sections (Qin Jiushao, 1247).^[5]

Proofs[edit]

There are many ways to prove Heron’s formula, for example using trigonometry as below, or the incenter and one excircle of the triangle,^[6] or as a special case of De Gua’s theorem (for the particular case of acute triangles),^[7] or as a special case of Brahmagupta’s formula (for the case of a degenerate cyclic quadrilateral).

Trigonometric proof using the law of cosines[edit]

A modern proof, which uses algebra and is quite different from the one provided by Heron, follows.^[8]
Let a, b, c be the sides of the triangle and α, β, γ the angles opposite those sides.
Applying the law of cosines we get

$cos gamma = frac{a^2+b^2-c^2}{2ab}$

From this proof, we get the algebraic statement that

$sin gamma = sqrt{1-cos^2 gamma} = frac{sqrt{4a^2 b^2 -(a^2 +b^2 -c^2)^2 }}{2ab}.$

The altitude of the triangle on base a has length b sin γ, and it follows

${displaystyle {begin{aligned}A&={tfrac {1}{2}}({mbox{base}})({mbox{altitude}})\[6mu]&={tfrac {1}{2}}absin gamma \[6mu]&={frac {ab}{4ab}}{sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}\[6mu]&={tfrac {1}{4}}{sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2a^{2}c^{2}+2b^{2}c^{2}}}\[6mu]&={tfrac {1}{4}}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\[6mu]&={sqrt {left({frac {a+b+c}{2}}right)left({frac {-a+b+c}{2}}right)left({frac {a-b+c}{2}}right)left({frac {a+b-c}{2}}right)}}\[6mu]&={sqrt {s(s-a)(s-b)(s-c)}}.end{aligned}}}$

Algebraic proof using the Pythagorean theorem[edit]

Triangle with altitude h cutting base c into d + (c − d)

The following proof is very similar to one given by Raifaizen.^[9]
By the Pythagorean theorem we have b² = h² + d² and a² = h² + (c − d)² according to the figure at the right. Subtracting these yields a² − b² = c² − 2cd. This equation allows us to express d in terms of the sides of the triangle:

${displaystyle d={frac {-a^{2}+b^{2}+c^{2}}{2c}}.}$

For the height of the triangle we have that h² = b² − d². By replacing d with the formula given above and applying the difference of squares identity we get

${displaystyle {begin{aligned}h^{2}&=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}\&={frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\&={frac {{big (}(b+c)^{2}-a^{2}{big )}{big (}a^{2}-(b-c)^{2}{big )}}{4c^{2}}}\&={frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\&={frac {2(s-a)cdot 2scdot 2(s-c)cdot 2(s-b)}{4c^{2}}}\&={frac {4s(s-a)(s-b)(s-c)}{c^{2}}}.end{aligned}}}$

We now apply this result to the formula that calculates the area of a triangle from its height:

${displaystyle {begin{aligned}A&={frac {ch}{2}}\&={sqrt {{frac {c^{2}}{4}}cdot {frac {4s(s-a)(s-b)(s-c)}{c^{2}}}}}\&={sqrt {s(s-a)(s-b)(s-c)}}.end{aligned}}}$

Trigonometric proof using the law of cotangents[edit]

Geometrical significance of s − a, s − b, and s − c. See the law of cotangents for the reasoning behind this.

If r is the radius of the incircle of the triangle, then the triangle can be broken into three triangles of equal altitude r and bases a, b, and c. Their combined area is

${displaystyle A={tfrac {1}{2}}ar+{tfrac {1}{2}}br+{tfrac {1}{2}}cr=rs,}$

where ${textstyle s={tfrac {1}{2}}(a+b+c)}$ is the semiperimeter.

The triangle can alternately be broken into six triangles (in congruent pairs) of altitude r and bases s − a, s − b, and s − c, of combined area (see law of cotangents)

${displaystyle {begin{aligned}A&=r(s-a)+r(s-b)+r(s-c)\[2mu]&=r^{2}left({frac {s-a}{r}}+{frac {s-b}{r}}+{frac {s-c}{r}}right)\[2mu]&=r^{2}left(cot {frac {alpha }{2}}+cot {frac {beta }{2}}+cot {frac {gamma }{2}}right)\[3mu]&=r^{2}left(cot {frac {alpha }{2}}cot {frac {beta }{2}}cot {frac {gamma }{2}}right)\[3mu]&=r^{2}left({frac {s-a}{r}}cdot {frac {s-b}{r}}cdot {frac {s-c}{r}}right)\[3mu]&={frac {(s-a)(s-b)(s-c)}{r}}.end{aligned}}}$

The middle step above is ${textstyle cot {tfrac {alpha }{2}}+cot {tfrac {beta }{2}}+cot {tfrac {gamma }{2}}=cot {tfrac {alpha }{2}}cot {tfrac {beta }{2}}cot {tfrac {gamma }{2}},}$ the triple cotangent identity, which applies because the sum of half-angles is ${textstyle {tfrac {alpha }{2}}+{tfrac {beta }{2}}+{tfrac {gamma }{2}}={tfrac {pi }{2}}.}$

Combining the two, we get

${displaystyle A^{2}=s(s-a)(s-b)(s-c),}$

from which the result follows.

Numerical stability[edit]

Heron’s formula as given above is numerically unstable for triangles with a very small angle when using floating-point arithmetic. A stable alternative^[10]^[11] involves arranging the lengths of the sides so that a ≥ b ≥ c and computing

${displaystyle A={frac {1}{4}}{sqrt {{big (}a+(b+c){big )}{big (}c-(a-b){big )}{big (}c+(a-b){big )}{big (}a+(b-c){big )}}}.}$

The brackets in the above formula are required in order to prevent numerical instability in the evaluation.

Similar triangle-area formulae[edit]

Three other formulae for the area of a general triangle have a similar structure as Heron’s formula, expressed in terms of different variables.

First, if m_a, m_b, and m_c are the medians from sides a, b, and c respectively, and their semi-sum is ${displaystyle sigma ={tfrac {1}{2}}(m_{a}+m_{b}+m_{c}),}$ then^[12]

$A = frac{4}{3} sqrt{sigma (sigma - m_a)(sigma - m_b)(sigma - m_c)}.$

Next, if h_a, h_b, and h_c are the altitudes from sides a, b, and c respectively, and semi-sum of their reciprocals is ${displaystyle H={tfrac {1}{2}}{bigl (}h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1}{bigr )},}$ then^[13]

${displaystyle A^{-1}=4{sqrt {H{bigl (}H-h_{a}^{-1}{bigr )}{bigl (}H-h_{b}^{-1}{bigr )}{bigl (}H-h_{c}^{-1}{bigr )}}}.}$

Finally, if α, β, and γ are the three angle measures of the triangle, and the semi-sum of their sines is ${displaystyle S={tfrac {1}{2}}(sin alpha +sin beta +sin gamma ),}$ then^[14]^[15]

${displaystyle {begin{aligned}A&=D^{2}{sqrt {S(S-sin alpha )(S-sin beta )(S-sin gamma )}}\[5mu]&={tfrac {1}{2}}D^{2}sin alpha ,sin beta ,sin gamma ,end{aligned}}}$

where D is the diameter of the circumcircle, ${textstyle D={frac {a}{sin alpha }}={frac {b}{sin beta }}={frac {c}{sin gamma }}.}$ This last formula coincides with the standard Heron formula when the circumcircle has unit diameter.

Generalizations[edit]

Heron’s formula is a special case of Brahmagupta’s formula for the area of a cyclic quadrilateral. Heron’s formula and Brahmagupta’s formula are both special cases of Bretschneider’s formula for the area of a quadrilateral. Heron’s formula can be obtained from Brahmagupta’s formula or Bretschneider’s formula by setting one of the sides of the quadrilateral to zero.

Brahmagupta’s formula gives the area K of a cyclic quadrilateral whose sides have lengths a, b, c, d as

where s, the semiperimeter, is defined to be

$s={frac {a+b+c+d}{2}}.$

Heron’s formula is also a special case of the formula for the area of a trapezoid or trapezium based only on its sides. Heron’s formula is obtained by setting the smaller parallel side to zero.

Expressing Heron’s formula with a Cayley–Menger determinant in terms of the squares of the distances between the three given vertices,

${displaystyle A={frac {1}{4}}{sqrt {-{begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}}}}$

illustrates its similarity to Tartaglia’s formula for the volume of a three-simplex.

Another generalization of Heron’s formula to pentagons and hexagons inscribed in a circle was discovered by David P. Robbins.^[16]

Heron-type formula for the volume of a tetrahedron[edit]

If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; u opposite to U and so on), then^[17]

${text{volume}}={frac {sqrt {,(-a+b+c+d),(a-b+c+d),(a+b-c+d),(a+b+c-d)}}{192,u,v,w}}$

where

Heron formulae in non-Euclidean geometries[edit]

There are also formulae for the area of a triangle in terms of its side lengths for triangles in the sphere or the hyperbolic plane. ^[18]
For a triangle in the sphere with side lengths a,b,c , half perimeter and area such a formula is

${displaystyle tan ^{2}{frac {S}{4}}=tan {frac {s}{2}}tan {frac {s-a}{2}}tan {frac {s-b}{2}}tan {frac {s-c}{2}}}$

while for the hyperbolic plane we have

${displaystyle tan ^{2}{frac {S}{4}}=tanh {frac {s}{2}}tanh {frac {s-a}{2}}tanh {frac {s-b}{2}}tanh {frac {s-c}{2}}.}$

References[edit]

^ Kendig, Keith (2000). “Is a 2000-year-old formula still keeping some secrets?”. The American Mathematical Monthly. 107 (5): 402–415. doi:10.1080/00029890.2000.12005213. JSTOR 2695295. MR 1763392. S2CID 1214184.
^ Id, Yusuf; Kennedy, E. S. (1969). “A medieval proof of Heron’s formula”. The Mathematics Teacher. 62 (7): 585–587. doi:10.5951/MT.62.7.0585. JSTOR 27958225. MR 0256819.
^ Heath, Thomas L. (1921). A History of Greek Mathematics. Vol. II. Oxford University Press. pp. 321–323.
^ Weisstein, Eric W. “Heron’s Formula”. MathWorld.
^ 秦, 九韶 (1773). “卷三上, 三斜求积”. 數學九章 (四庫全書本) (in Chinese).
^ “Personal email communication between mathematicians John Conway and Peter Doyle”. 15 December 1997. Retrieved 25 September 2020.
^ Lévy-Leblond, Jean-Marc (2020-09-14). “A Symmetric 3D Proof of Heron’s Formula”. The Mathematical Intelligencer. 43 (2): 37–39. doi:10.1007/s00283-020-09996-8. ISSN 0343-6993.
^ Niven, Ivan (1981). Maxima and Minima Without Calculus. The Mathematical Association of America. pp. 7–8.
^ Raifaizen, Claude H. (1971). “A Simpler Proof of Heron’s Formula”. Mathematics Magazine. 44 (1): 27–28. doi:10.1080/0025570X.1971.11976093.
^ Sterbenz, Pat H. (1974-05-01). Floating-Point Computation. Prentice-Hall Series in Automatic Computation (1st ed.). Englewood Cliffs, New Jersey, USA: Prentice Hall. ISBN 0-13-322495-3.
^ William M. Kahan (24 March 2000). “Miscalculating Area and Angles of a Needle-like Triangle” (PDF).
^ Benyi, Arpad, “A Heron-type formula for the triangle,” Mathematical Gazette 87, July 2003, 324–326.
^ Mitchell, Douglas W., “A Heron-type formula for the reciprocal area of a triangle,” Mathematical Gazette 89, November 2005, 494.
^ Mitchell, Douglas W. (2009). “A Heron-type area formula in terms of sines”. Mathematical Gazette. 93: 108–109. doi:10.1017/S002555720018430X. S2CID 132042882.
^ Kocik, Jerzy; Solecki, Andrzej (2009). “Disentangling a triangle” (PDF). American Mathematical Monthly. 116 (3): 228–237. doi:10.1080/00029890.2009.11920932. S2CID 28155804.
^ D. P. Robbins, “Areas of Polygons Inscribed in a Circle”, Discr. Comput. Geom. 12, 223-236, 1994.
^ W. Kahan, “What has the Volume of a Tetrahedron to do with Computer Programming Languages?”, [1], pp. 16–17.
^ Page 66 in Alekseevskij, D. V.; Vinberg, E. B.; Solodovnikov, A. S. (1993), “Geometry of spaces of constant curvature”, in Gamkrelidze, R. V.; Vinberg, E. B. (eds.), Geometry. II: Spaces of constant curvature, Encycl. Math. Sci., vol. 29, Springer-Verlag, pp. 1–138, ISBN 1-56085-072-8

External links[edit]

A Proof of the Pythagorean Theorem From Heron’s Formula at cut-the-knot
Interactive applet and area calculator using Heron’s Formula
J. H. Conway discussion on Heron’s Formula
“Heron’s Formula and Brahmagupta’s Generalization”. MathPages.com.
A Geometric Proof of Heron’s Formula
An alternative proof of Heron’s Formula without words
Factoring Heron

Источник

Приветствую Вас, уважаемые Читатели! Предлагаю вспомнить школьные годы, когда Вы только начинали познавать азы геометрии. Еще в седьмом классе учитель обязательно рассказывал Вам о различных способах нахождения площади треугольника. Особняком среди различных подходов стояла формула Герона, связывающая площадь треугольника с его полупериметром.

Герон Александрийский. Источник: https://www.ilovegreece.ru/mediaResource/00/010/009.jpg

К сожалению, по моим школьным воспоминаниям попытки применить в той или иной задаче формулу Герона практически всегда приводили в тупик: тут и там возникали уравнения высших степеней и процесс стопорился.

Вот чего в школе не рассказывали, так это того, откуда выводится эта замечательная, не лишенная изящества, формула. Поехали!

Итак, дан произвольный треугольник. Сначала воспользуемся формулой площади через две стороны и угол между ними:

Формула, которую в школе знал каждый, но никто не знал, откуда она появилась

Почему используется основное тригонометрическое тождество для преобразования синуса в косинус? А потому, что дальше мы будем применять теорему косинусов:

Теперь нам лишь необходимо совместить две формулы. Процесс вроде несложный, то требуется последовательного поиска разностей/сумм квадратов и квадратов разностей/сумм в нагромождении символов:

И вот она, замечательная формула Герона, в которой p обозначает полупериметр треугольника:

Надеюсь, все её признали! Спасибо за внимание!

Конспект урока: Формула Герона

Площади

План урока

Вклад в математику Герона Александрийского.
Формула Герона.
Примеры применения формулы Герона.

Цели урока

Знать формулу Герона.
Уметь применять формулу Герона для решения задач.

Разминка

Как вычислить площадь треугольника?
Выразите катет прямоугольного треугольника через гипотенузу и другой катет?
Как разложить на множители разность квадратов?

Историческая справка

Рис. 1. Герон Александрийский

Геро́н Александри́йский (др.-греч. Ἥρων ὁ Ἀλεξανδρεύς) — греческий математик и механик (Рис. 1).

Время жизни отнесено ко второй половине I века н. э. на том основании, что он приводит в качестве примера лунное затмение 13 марта 62 г. н. э. Подробности его жизни неизвестны.

Герона относят к величайшим инженерам за всю историю человечества. Он первым изобрёл автоматические двери, автоматический театр кукол, автомат для продаж, скорострельный самозаряжающийся арбалет, паровую турбину, автоматические декорации, прибор для измерения протяжённости дорог (древний одометр) и др. Первым начал создавать программируемые устройства: вал со штырьками с намотанной на него верёвкой.

Занимался геометрией, механикой, гидростатикой, оптикой. Основные произведения: «Метрика», «Пневматика», «Автоматопоэтика», «Механика» (произведение сохранилось целиком в арабском переводе), «Катоптрика» (наука о зеркалах; сохранилась только в латинском переводе) и др. В 1814 году было найдено сочинение Герона «О диоптре», в котором изложены правила земельной съёмки, фактически основанные на использовании прямоугольных координат. Герон использовал достижения своих предшественников: Евклида, Архимеда, Стратона из Лампсака.

Многие из его книг безвозвратно утеряны (свитки содержались в Александрийской библиотеке). Одна из копий его книг, сделанная в XVI веке, содержится в Оксфордском Университете.

В средние века многие из его изобретений были отвергнуты, забыты или не представляли практического интереса.

«Метрика» (Μετρική) Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений:

Целочисленные героновы треугольники.
Формулы для площадей правильных многоугольников.
Объёмы правильных многогранников, пирамиды, конуса, усечённого конуса, тора, шарового сегмента.
Формула Герона для расчёта площади треугольника по длинам его сторон (открытая Архимедом).
Правила численного решения квадратных уравнений.
Алгоритмы извлечения квадратных и кубических корней.

В основном изложение в математических трудах Герона догматично: правила часто не выводятся, а только показываются на примерах.

Книга Герона «Определения» представляет собой обширный свод геометрических определений, по большей части совпадающих с определениями «Начал» Евклида.

Теорема (формула Герона)

Площадь S треугольника со сторонами a, b, c выражается формулой

S=p(p-a)(p-b)(p-c),

где p=a+b+c2 — полупериметр треугольника.

Доказательство

Рис. 2. К доказательству формулы Герона

Рассмотрим треугольник ABC, в котором AB=a, BC=b, AC=c, p=a+b+c2. Пусть углы A и C острые, проведем высоту BD=h из вершины большего угла треугольника.

Обозначим AD=x, CD=y (Рис. 2). По теореме Пифагора выразим высоту BD из прямоугольных треугольников ABD и CBD:

h2=a2-x2=b2-y2.

Следовательно, a2-b2=x2-y2, откуда (x+y)(x-y)=a2-b2. Так как x+y=c, то x-y=1c(a2-b2). Выразим x, сложив два последних равенства и поделив на 2:

x=a2+c2-b22c.

Тогда,

h2=a2-x2=(a-x)(a+x)=(a-a2+c2-b22c)(a+a2+c2-b22c)=

=b2-(a-c)22c×(a+c)2-b22c=(b+c-a)(b+a-c)(a+c-b)(a+c+b)4c2.

Поскольку

p=a+b+c2,

то a+b+c=2p и b+c=2p-a, b+a=2p-c, a+c=2p-b.

Тогда

(b+c-a)(b+a-c)(a+c-b)(a+c+b)4c2=

=(2p-2a)(2p-2c)(2p-2b)2p4c2=4p(p-a)(p-b)(p-c)c2.

Следовательно,

h=2p(p-a)(p-b)(p-c)c.

S=12c×h=12c×2p((p-a)(p-b)(p-c)c=p(p-a)(p-b)(p-c).

Теорема доказана.

Пример 1

Найдите площадь треугольника со сторонами 5, 5, 6.

Решение

Для вычисления площади используем формулу Герона:

p=5+5+62=8.

S=8×(8-5)×(8-5)×(8-6)=8×3×3×2=12.

Ответ: 12.

Пример 2

Найдите наименьшую высоту треугольника со сторонами 13, 14 и 15.

Решение

Для решения задачи используем метод площадей: вычислим площадь треугольника, используя формулу Герона, а после, используя теорему о площади треугольника, вычислим высоту треугольника. Поскольку площадь треугольника величина постоянная, то меньшая высота проведена к большей стороне.

p=13+14+152=21,

S=21×(21-13)×(21-14)×(21-15)=21×8×7×6=84.

Обозначим искомую высоту h:

S=12×15×h, h=8412×15=11,2.

Ответ: 11,2.

Пример 3

Основания трапеции равны 20 см и 60 см, а боковые стороны — 13 см и 37 см. Найдите площадь трапеции.

Решение

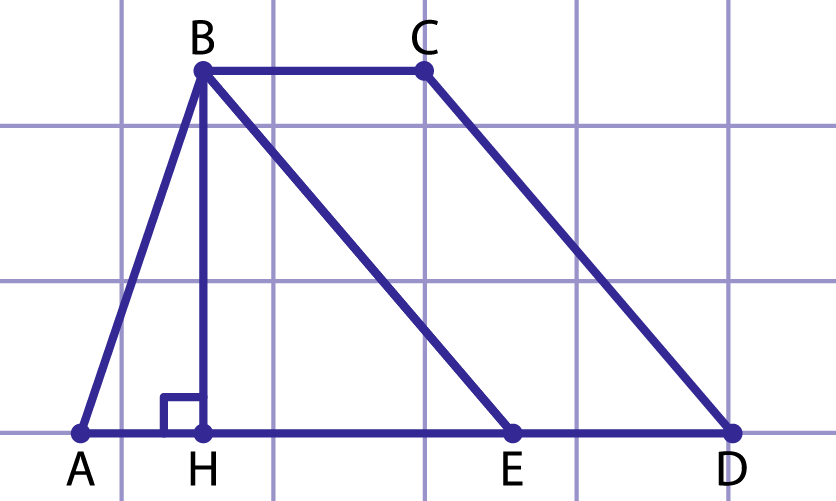
Рис. 3. К решению примера 3

Рассмотрим трапецию ABCD, AB=13 см, BC=20 см, AD=60 см, CD=37 см (Рис. 3). Проведем прямую BE параллельную CD, по определению BCDE — параллелограмм, тогда BC=DE, BE=CD.

AE=AD-DE=60-20=40 (см).

Высота треугольника ABE совпадает с высотой трапеции ABCD. Вычислим высоту BH как показано в примере 2 с применением формулы Герона:

p=13+37+402=45 (см).

S=45×(45-13)×(45-37)×(45-40)=240 (см2).

BH=24012×40=12 см.

Зная высоту и длины оснований трапеции, вычислим площадь:

SABCD=12×(20+60)×12=480 (см2).

Ответ: 480 см2.

Упражнения

1. Найдите площадь треугольника со сторонами 29 см, 25 см, 6 см.

2. Найдите наименьшую высоту треугольника со сторонами 15 см, 13 см и 4 см.

3. Вычислите площадь параллелограмма, стороны которого равны 1 дм и 9 см, а одна из диагоналей равна 17 см.

Контрольные вопросы

1. Сформулируйте формулу Герона.

2. Приведите пример задачи, в которой площадь треугольника можно вычислить с помощью формулы Герона, но нельзя вычислить с помощью теоремы о площади треугольника.

1. 60 см2.

2. 3,2 см.

3. 72 см2.

Предыдущий урок

Площадь параллелограмма. Площадь треугольника

Площади

Следующий урок

Осевая и центральная симметрии

Общие геометрические сведения

Источник

Вариации и обобщения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Формула Герона

Формулировка теоремы Герона

Формула и доказательство

Для каких треугольников действует теорема

Примеры решения задач

Example[edit]

Alternate expressions[edit]

History[edit]

Proofs[edit]

Trigonometric proof using the law of cosines[edit]

Algebraic proof using the Pythagorean theorem[edit]

Trigonometric proof using the law of cotangents[edit]

Numerical stability[edit]

Similar triangle-area formulae[edit]

Generalizations[edit]

Heron-type formula for the volume of a tetrahedron[edit]

Heron formulae in non-Euclidean geometries[edit]

See also[edit]

References[edit]

External links[edit]

Читайте также:

Конспект урока: Формула Герона

Площади

Добавить комментарий Отменить ответ

Вариации и обобщения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Формула Герона

Формулировка теоремы Герона

Формула и доказательство

Для каких треугольников действует теорема

Примеры решения задач

Example[edit]

Alternate expressions[edit]

History[edit]

Proofs[edit]

Trigonometric proof using the law of cosines[edit]

Algebraic proof using the Pythagorean theorem[edit]

Trigonometric proof using the law of cotangents[edit]

Numerical stability[edit]

Similar triangle-area formulae[edit]

Generalizations[edit]

Heron-type formula for the volume of a tetrahedron[edit]

Heron formulae in non-Euclidean geometries[edit]

See also[edit]

References[edit]

External links[edit]

Читайте также:

Конспект урока: Формула Герона

Площади

Вам также может понравиться

Как найти выставку динозавров

Как найти настройки провайдера

Правила как составить синквейн

Добавить комментарий Отменить ответ