Тип урока: Обобщение, закрепление
пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического
способа решения уравнений; - закрепление навыков записи и
копирования формул, построения графиков
функций в электронных таблицах Excel 2007; - формирование и первичное закрепление
знаний о решении уравнений с
использованием возможностей электронных
таблиц Excel 2007; - формирование мышления, направленного на
выбор оптимального решения; - формирование информационной культуры
школьников.
Оборудование: персональные
компьютеры, мультимедиапроектор,
проекционный экран.
Материалы к уроку: презентация Power Point
на компьютере учителя (Приложение 1).
Ход урока
Организационный момент.
Слайд 1 из Приложения1 ( далее
ссылки на слайды идут без указания
Приложения1).
Объявление темы урока.
1. Устная работа (актуализация
знаний).
Слайд 2 – Соотнесите перечисленные
ниже функции с графиками на чертеже (Рис. 1):
у = 6 – х; у = 2х + 3; у = (х + 3)2; у = -(х – 4)2;
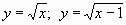 .
.
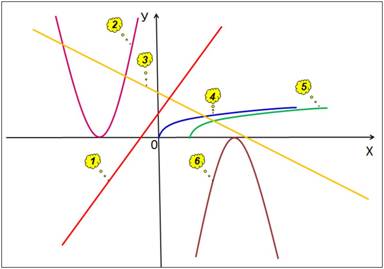
Рис. 1.
Слайд 3 Графический способ решения
уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются
значения х1, х2, … точек
пересечения графика функции y=f(x) с осью
абсцисс (Рис. 2).
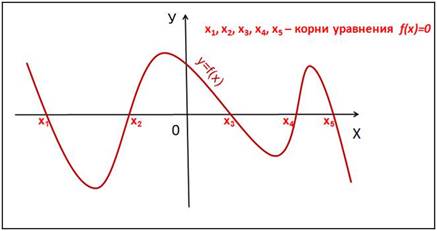
Рис. 2.
Слайд 4
Найдите корни уравнения х2-2х-3=0,
используя графический способ решения
уравнений (Рис.3).
Ответ: -1; 3.
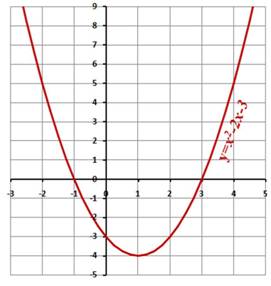
Рис. 3.
Слайд 5 Графический способ решения
уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются
значения х1, х2, … точек
пересечения графиков функций y=f(x) и у=g(x).
(Рис. 4):
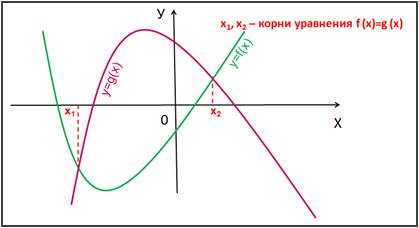
Рис. 4.
Слайд 6 Найдите корни уравнения 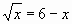 ,
,
используя графический способ решения
уравнений (Рис. 5).
Ответ: 4.
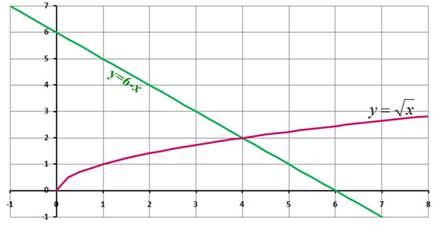
Рис. 5.
2. Объяснение нового материала.
Практическая работа.
Решение уравнений графическим способом
требует больших временных затрат на
построение графиков функций и в
большинстве случаев дает грубо
приближенные решения. При использовании
электронных таблиц, в данном случае – Microsoft
Excel 2007, существенно экономится время на
построение графиков функций, и появляются
дополнительные возможности нахождения
корней уравнения с заданной точностью (метод
Подбор параметра).
I. Графический способ решения
уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в
Excel одновременно с учениками с подробными (при
необходимости) инструкциями и выводом
результатов на проекционный экран. Слайды
Приложения 1 используются для формулировки
задач и подведения промежуточных итогов.
Слайд 7
Пример1: Используя средства построения
диаграмм в Excel, решить графическим способом
уравнение –х2+5х-4=0.
Для этого: построить график функции у=-х2+5х-4
на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения
графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в
табличной форме (рис. 6):

Рис. 6.
Для этого:
- в ячейку А1 ввести текст Х, в
ячейку A2 — Y; - в ячейку В1 ввести число 0, в ячейку С1
– число 0,25; - выделить ячейки В1:С1, подвести
указатель мыши к маркеру выделения, и в
тот момент, когда указатель мыши примет
форму черного крестика, протянуть маркер
выделения вправо до ячейки V1 (Рис. 7).

Рис. 7.
- в ячейку B2 ввести формулу =-(B1^2)+5*B1-4;
При вводе формулы можно
вводить адрес ячейки с клавиатуры (не
забыть переключиться на латиницу), а
можно просто щелкнуть мышью на ячейке с
нужным адресом.
После ввода формулы в ячейке
окажется результат вычисления по
формуле, а в поле ввода строки формул –
сама формула (Рис. 8):
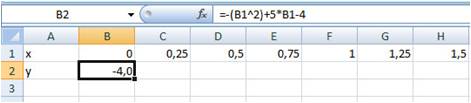
Рис. 8.
- скопировать содержимое ячейки B2 в
ячейки C2:V2 за маркер выделения. Весь
ряд выделенных ячеек заполнится
содержимым первой ячейки. При этом ссылки
на ячейки в формулах изменятся
относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
Для этого:
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График
выбрать вид График; - на вкладке Конструктор|Выбрать данные
(Рис. 9) в открывшемся окне «Выбор
источника данных» щелкнуть по кнопке Изменить
в поле Подписи горизонтальной оси –
откроется окно «Подписи оси». Выделить в
таблице диапазон ячеек B1:V1 (значения
переменной х). В обоих окнах щелкнуть
по кнопкам ОК;
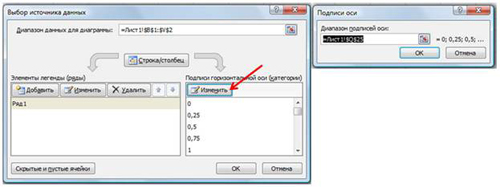
Рис. 9.
- на вкладке Макет|Оси|Основная
горизонтальная ось|Дополнительные
параметры основной горизонтальной оси
выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица
измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки
Тип
линии и Цвет линии);
- самостоятельно изменить ширину и цвет
линии для вертикальной оси; - на вкладке Макет|Сетка|Вертикальные
линии сетки по основной оси выбрать Основные
линии сетки.
Примерный результат работы приведен на
рис. 10:
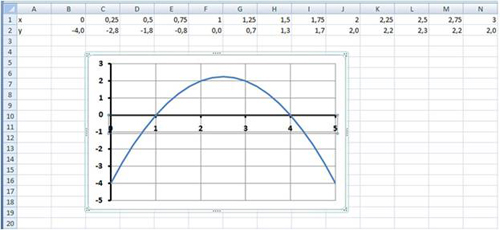
Рис. 10.
3 этап: Определение корней уравнения.
График функции у=-х2+5х-4
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня: х1=1; х2=4.
II. Графический способ решения уравнений
вида f(x)=g(x) в Excel.
Слайд 8
Пример 2: Решить графическим способом
уравнение 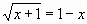 .
.
Для этого: в одной системе координат
построить графики функций у1=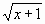
и у2=1-х
на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки
пересечения графиков функций.
1 этап: Представление функций в
табличной форме (рис. 1):
- Перейти на Лист2.
- Аналогично Примеру 1, применив
приемы копирования, заполнить таблицу.
При табулировании функции у1=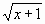
воспользоваться встроенной функцией Корень
(Рис. 11).

Рис. 11.
2 этап: Построение диаграммы типа График.
- Выделить диапазон ячеек (А2:V3);
- Аналогично Примеру 1 вставить и
отформатировать диаграмму типа График,
выбрав дополнительно в настройках
горизонтальной оси: вертикальная ось
пересекает в категории с номером 5.
Примерный результат работы приведен на
Рис. 12:
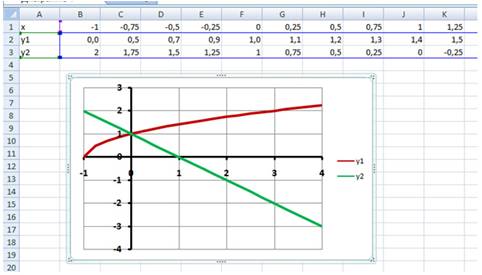
Рис. 12.
3 этап: Определение корней уравнения.
Графики функций у1=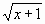
и у2=1-х пересекаются в одной
точке (0;1) и, следовательно, уравнение 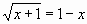
имеет один корень – абсцисса этой точки: х=0.
III. Метод Подбор параметра.
Слайд 9
Графический способ решения уравнений
красив, но далеко не всегда точки
пересечения могут быть такими «хорошими»,
как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц
позволяют находить приближенные значения
коней уравнения с заданной точностью. Для
этого используется метод Подбор
параметра.
Слайд 10
Пример 3: Разберем метод Подбор
параметра на примере решения уравнения –х2+5х-3=0.
1 этап: Построение диаграммы типа График
для приближенного определения корней
уравнения.
Построить график функции у=–х2+5х-3,
отредактировав полученные в Примере 1
формулы.
Для этого:
- выполнить двойной щелчок по ячейке B2,
внести необходимые изменения; - с помощью маркера выделения
скопировать формулу во все ячейки
диапазона C2:V2.
Все изменения сразу отобразятся на
графике.
Примерный результат работы приведен на
Рис. 13:
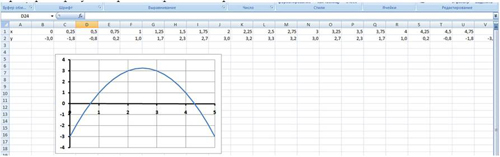
Рис. 13.
2 этап: Определение приближенных
значений корней уравнения.
График функции у=-х2+5х-3
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня.
По графику приближенно можно
определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения
уравнения с заданной точностью методом Подбор
параметра.
1) Начать с поиска более точного
значения меньшего корня.
По графику видно, что ближайший
аргумент к точке пересечения графика с
осью абсцисс равен 0,75. В таблице
значений функции этот аргумент
размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор
параметра…;
В открывшемся диалоговом окне Подбор
параметра (Рис. 14) в поле Значение
ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки:
ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
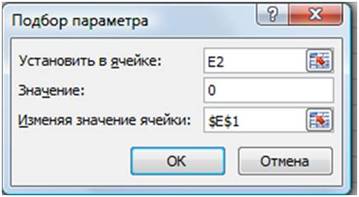
Рис. 14.
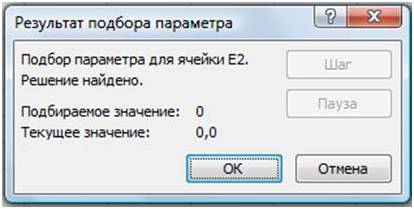
Рис. 15.
- В окне Результат подбора (Рис. 15)
выводится информация о величине
подбираемого и подобранного значения
функции: - В ячейке E1 выводится подобранное
значение аргумента 0,6972 с требуемой
точностью (0,0001).
Установить точность можно путем
установки в ячейках таблицы точности
представления чисел – числа знаков
после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения
определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение
большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для
решения уравнений вида f(x)=g(x).
При использовании метода Подбор
параметров для решения уравнений вида f(x)=g(x)
вводят вспомогательную функцию y(x)=f(x)-g(x)
и находят с требуемой точностью значения х
точек пересечения графика функции y(x) с
осью абсцисс.
3. Закрепление изученного материала. Самостоятельная
работа.
Слайд 11
Задание: Используя метода Подбор
параметров, найти корни уравнения 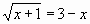
с точностью до 0,001.
Для этого:
- ввести функцию у=
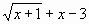
и построить ее график на промежутке [ -1; 4 ] с
шагом 0,25 (Рис. 16):
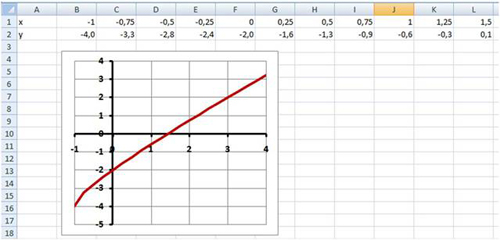
Рис. 16.
- найти приближенное значение х
точки пересечения графика функции с
осью абсцисс (х≈1,4); - найти приближенное решение уравнения с
точностью до 0,001 методом Подбор
параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной
работы.
Слайд 13 Повторение графического
способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического
способа решения уравнения вида f(x)=g(x).
Выставление оценок.
5. Домашнее задание.
Слайд 15 .
Используя средства построения диаграмм
в Excel и метод Подбор параметра, определите
корни уравнения х2-5х+2=0 с
точностью до 0,01.
Нахождение корней уравнения и уточнение их значений средствами MS Excel.



Работа 5.
Рассмотрим пример нахождения всех вещественных корней уравнения в заданном интервале [-1;1] независимой переменной x
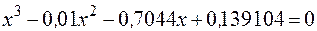
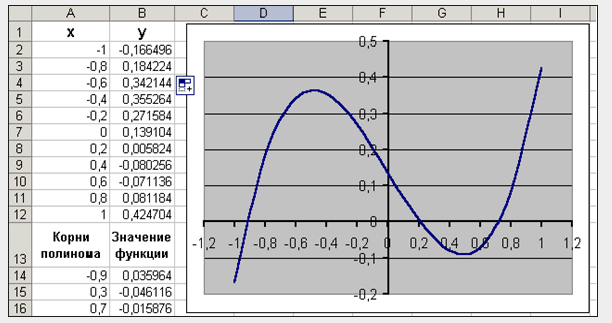
Отметим, что у полинома третей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно нужно локализовать. С этой целью табулируем функцию в заданном интервале и построим график (рис. 1, табл.1) Например, на отрезке [-1;1]. Результат табуляции приведён на рис.1, где в ячейку С7 введена следующая формула:
= B7^3-0.01*B7^2-0,7044*B7+0,139104
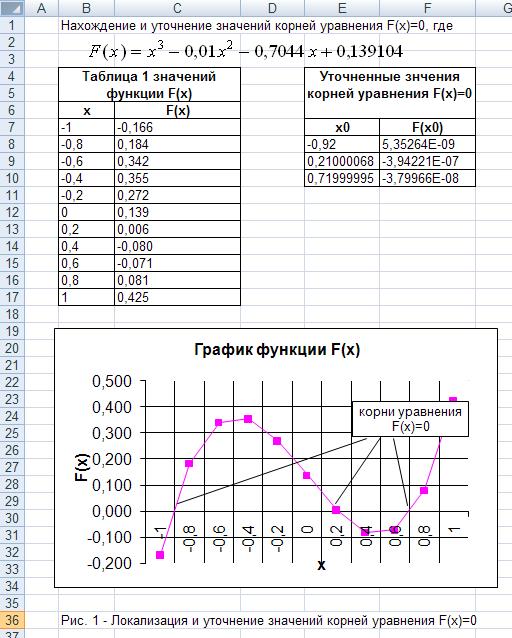
Из рисунка видно, что полином меняет знак на интервалах [-1,-08], [0.2, 0.4] и [0.6, 0.8]. Это означает, что на каждом из них имеется корень данного полинома. И, как видно из графика, эти корни приблизительно равны x0=-0.9, x1=0.2 и x3=0.7.
Уточним значения корней, используя встроенную в MS Excel процедуру Подбор параметра.
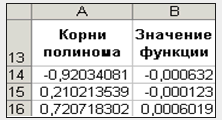
Предварительно построим отдельную таблицу для уточнения значения корней (рис.1, табл. 2).
В клетку E8 введем приближенное значение 1-го корня -0,9. В клетку F8 введём формулу = E8^3-0,01*E8^2-0,7044*E8+0,139104
Данные, Анализ «что-если», Подбор параметра, Установить в ячейке: F8, Значение: 0, Изменяя значение ячейки: $E$8, Ok.
В диалоговом окне Подбора параметра просматриваем значение полинома при найденном значении корня и нажимаем Ok.
Найденное значение корня MS Excel помещает в клетку E8.
Аналогично можно уточнить взятые из графика значения других корней уравнения. В качестве начальных значений корней взяты х=0.3 и х=0.7
Варианты индивидуальных заданий
1. Построив график функции f(x), определите грубо интервал [a,b] расположения корней уравнения f(x) = 0;
2. Используя приёмы, рассмотренные выше, найдите более точные значения корней с относительной погрешностью не более 0,0001.
| № | f(x) | f(x) |
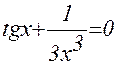 |
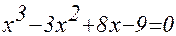 |
|
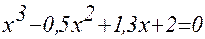 |
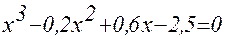 |
|
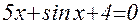 |
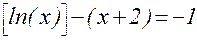 |
|
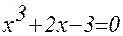 |
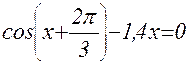 |
|
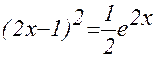 |
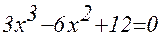 |
|
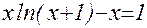 |
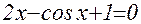 |
|
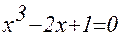 |
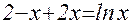 |
|
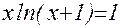 |
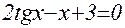 |
|
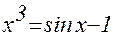 |
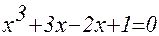 |
|
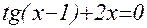 |
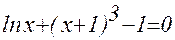 |
|
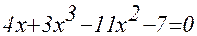 |
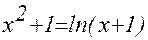 |
|
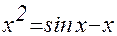 |
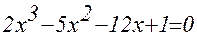 |
|
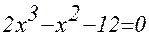 |
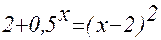 |
|
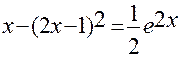 |
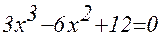 |
|
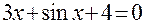 |
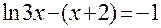 |
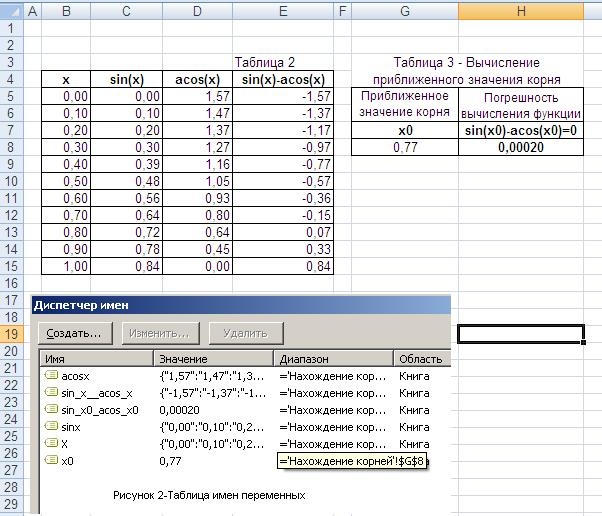
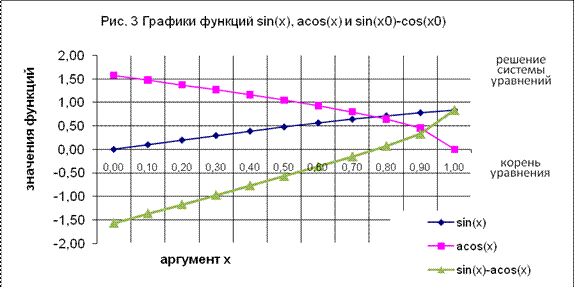
Ниже приведён пример вычисления уточненного значения корня уравнения sin(x)-acos(x)=0,
при выбранном x0=0,7.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Прямо сейчас студенты читают про:
По способу восприятия сигналы подразделяются на видимые и звуковые Видимые сигналы выражаются: цветом, формой, положением и числом сигнальных показаний.
Рационализм. Рене Декарт Решающая роль разума в процессе познания. Рационализм (от лат. rationalis — «разумный») в противовес.
Столыпинская аграрная реформа: цели, основные направления, содержание, результаты, значение В российском обществе важнейшим вопросом всегда был аграрный. Крестьяне.
Симметрия относительно плоскости Постановка задачи. Найти координаты точки , симметричной точке относительно плоскости . План решения. 1. Находим уравнение прямой.
Химическая посуда и другие принадлежности В каждой лаборатории необходима химическая посуда, которая может быть разделена на ряд групп.
Источник
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ;  .
.

Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).

Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).

Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):

Слайд 6 Найдите корни уравнения  , используя графический способ решения уравнений (Рис. 5).
, используя графический способ решения уравнений (Рис. 5).

2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):

- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).

При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):

- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;

- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:

3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение  .
.
Для этого: в одной системе координат построить графики функций у1=  и у2=1-х на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки пересечения графиков функций.
и у2=1-х на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки пересечения графиков функций.
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).
2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:

3 этап: Определение корней уравнения.
Графики функций у1=  и у2=1-х пересекаются в одной точке (0;1) и, следовательно, уравнение
и у2=1-х пересекаются в одной точке (0;1) и, следовательно, уравнение  имеет один корень – абсцисса этой точки: х=0.
имеет один корень – абсцисса этой точки: х=0.
III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:

2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.


- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения  с точностью до 0,001.
с точностью до 0,001.
- ввести функцию у=
 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):

- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Источник
Применение табличного процессора Microsoft Excel для
графического решения уравнений n-ой степени
·
Москалёва
Елена Александровна
·
Разделы: Математика, Информатика
Из курса математики
известно, что корнями уравнения являются значения точек пересечения графика
функции с осью абсцисс. Если же мы решаем систему уравнений, то ее решениями
будут координаты точек пересечения графиков функций. Этот метод нахождения
корней уравнения называется графическим. Мы уже знаем, что с помощью EXCEL
можно строить практически любые графики. Воспользуемся этими знаниями для
нахождения корней системы уравнений:

Преобразуем данную систему в приведенную:

Для оценки решений воспользуемся диаграммой, на которой
отобразим графики обеих функций. Сначала построим таблицу:
Первая строка – строка заголовков.
При заполнении столбца А: в ячейку А2 заносится начальное
значение аргумента Х = – 10, для автоматического заполнения всего столбца в
ячейку А3 занести формулу “= А2 + 1” и скопировать ее до ячейки А22.
При заполнении столбца В: в ячейку В2 заносится формула “= А2 *
А2”, которая затем копируется до ячейки В22.
При заполнении столбца С: в ячейку С2 заносится формула “ = 2 *
А2 + 9”, и также копируется до С22

Рисунок 1
С помощью Мастера диаграмм построим в одной координатной
плоскости графики заданных функций для первоначальной оценки решений/

Рисунок 2
На диаграмме видно, что оба графика имеют точки пересечения –
координаты этих точек и есть решения системы. Так как шаг изменения аргумента
достаточно велик, то мы получим приближенные значения решений.

Рисунок 3
Уточним их, построив два графика в интервалах от – 3 до 0, где
находится первое решение, и от 3 до 5, где находится второе решение. Составим
новые таблицы. Для первого решения – рисунок 4, для второго – рисунок 5.

Рисунок 4

Рисунок 5
Для более точного построения мы уменьшили шаг изменения
аргумента. Решением нашей системы будут координаты точек пересечения графиков:
Х1 = – 2,2; Y1 =
4,6; Х2 = 4,2; Y2 =
17,4. Как вы уже поняли, графическое решение системы дает приблизительные результаты.
Это можно сделать, построив график и определив координаты точек его пересечения
с осью OX, либо построив два графика: Y = X3;
Y = 2X2 + 4X – 12 и определив точки их пересечения.

Рисунок 6
Решение нелинейных
уравнений и систем»
Цель работы:
Изучение возможностей пакета Ms Excel 2007
при решении нелинейных уравнений и
систем. Приобретение навыков решения
нелинейных уравнений и систем средствами
пакета.
Задание1.
Найти корни
полинома x3
– 0,01x2
– 0,7044x + 0,139104 = 0.
Для начала решим
уравнение графически. Известно, что
графическим решением уравнения f(x)=0
является точка пересечения графика
функции f(x) с осью абсцисс, т.е. такое
значение x, при котором функция обращается
в ноль.
Проведем табулирование
нашего полинома на интервале от -1 до 1
с шагом 0,2. Результаты вычислений
приведены на ри., где в ячейку В2 была
введена формула: = A2^3 – 0,01*A2^2 – 0,7044*A2 +
0,139104. На графике видно, что функция три
раза пересекает ось Оx, а так как полином
третьей степени имеется не более трех
вещественных корней, то графическое
решение поставленной задачи найдено.
Иначе говоря, была проведена локализация
корней, т.е. определены интервалы, на
которых находятся корни данного полинома:
[-1,-0.8], [0.2,0.4] и [0.6,0.8].
Теперь можно найти
корни полинома методом последовательных
приближений с помощью команды
Данные→Работа с данными→Анализ
«Что-Если» →Подбор параметра.
После ввода
начальных приближений и значений функции
можно обратиться к команде Данные→Работа
с данными→Анализ «Что-Если» →Подбор
параметра
и заполнить диалоговое окно следующим
образом.

В поле Установить
в ячейке дается
ссылка на ячейку, в которую введена
формула, вычисляющая значение левой
части уравнения (уравнение должно быть
записано так, чтобы его правая часть не
содержала переменную). В поле Значение
вводим правую часть уравнения, а в поле
Изменяя
значения ячейки
дается ссылка на ячейку, отведенную под
переменную. Заметим, что вводить ссылки
на ячейки в поля диалогового окна Подбор
параметров
удобнее не с клавиатуры, а щелчком на
соответствующей ячейке.
После нажатия
кнопки ОК появится диалоговое окно
Результат подбора параметра с сообщением
об успешном завершении поиска решения,
приближенное значение корня будет
помещено в ячейку А14.

Два оставшихся
корня находим аналогично. Результаты
вычислений будут помещены в ячейки А15
и А16.
Задание 2. Решить
уравнение ex–
(2x – 1)2
= 0.
Проведем локализацию
корней нелинейного уравнения.
Для этого представим
его в виде f(x) = g(x) , т.е. ex
= (2x – 1)2
или f(x) = ex,
g(x) = (2x – 1)2,
и решим графически.
Графическим
решением уравнения f(x) = g(x) будет точка
пересечения линий f(x) и g(x).
Построим графики
f(x) и g(x). Для этого в диапазон А3:А18 введем
значения аргумента. В ячейку В3 введем
формулу для вычисления значений функции
f(x): = EXP(A3), а в С3 для вычисления g(x): =
(2*A3-1)^2.
Результаты
вычислений и построение графиков f(x) и
g(x):

На графике видно,
что линии f(x)
и g(x)
пересекаются дважды, т.е. данное уравнение
имеет два решения. Одно из них тривиальное
и может быть вычислено точно:

Для второго можно
определить интервал изоляции корня:
1,5 < x
< 2.
Теперь можно найти
корень уравнения на отрезке [1.5,2] методом
последовательных приближений.
Введём начальное
приближение в ячейку Н17 = 1,5, и само
уравнение, со ссылкой на начальное
приближение, в ячейку I17
= EXP(H17)
– (2*H17-1)^2.
Далее воспользуемся
командой
Данные→Работа с данными→Анализ
«Что-Если» →Подбор параметра.
и заполним
диалоговое окно Подбор
параметра.

Результат поиска
решения будет выведен в ячейку Н17.

Задание 3.
Решить
систему уравнений:

Прежде чем
воспользоваться описанными выше методами
решения систем уравнений, найдем
графическое решение этой системы.
Отметим, что оба уравнения системы
заданы неявно и для построения графиков,
функций соответствующих этим уравнениям,
необходимо разрешить заданные уравнения
относительно переменной y.
Для первого
уравнения системы имеем:
![]()
Выясним ОДЗ
полученной функции:

Второе уравнение
данной системы описывает окружность.
Фрагмент рабочего
листа MS Excel с формулами, которые необходимо
ввести в ячейки для построения линий,
описанных уравнениями системы. Точки
пересечения линий изображенных являются
графическим решением системы нелинейных
уравнений.

Не трудно заметить,
что заданная система имеет два решения.
Поэтому процедуру поиска решений системы
необходимо выполнить дважды, предварительно
определив интервал изоляции корней по
осям Оx и Oy . В нашем случае первый корень
лежит в интервалах (-0.5;0)x
и (0.5;1)y,
а второй – (0;0.5)x
и (-0.5;-1)y.
Далее поступим следующим образом. Введем
начальные значения переменных x и y,
формулы отображающие уравнения системы
и функцию цели.

Теперь дважды
воспользуемся командой Данные→Анализ→Поиск
решений, заполняя появляющиеся диалоговые
окна.


Сравнив полученное
решение системы с графическим, убеждаемся,
что система решена верно.

Задания для
самостоятельного решения
Задание
1.
Найти корни полинома
Задание 2.
Найдите решение нелинейного уравнения.
Задание
3.
Найдите решение системы нелинейных
уравнений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
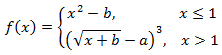
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
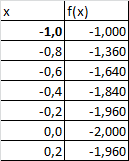
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
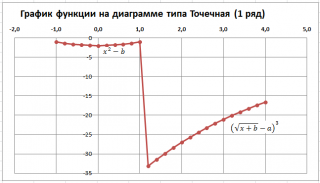
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
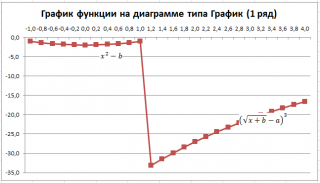
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
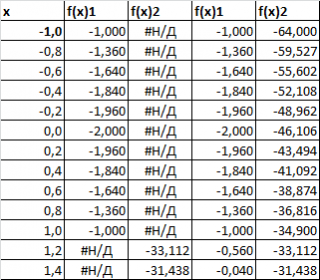
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
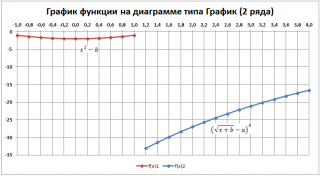
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Практическая работа “Графический метод решения уравнений в Excel”

Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Просмотр содержимого документа
«Практическая работа «Графический метод решения уравнений в Excel»»
Графический метод решения уравнений.
Найти графическим методом корень уравнения 10sin(x)-2x 2 +5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.

Исследование физических моделей
Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол, при котором дальность полета будет максимальной.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;
изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с 2 и движение по оси OY можно считать равноускоренным;
скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.
2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:
Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:
 или
или 
 или
или 
3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.
Использование графических возможностей Excel для решения математических задач
методическая разработка по алгебре на тему

Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
Скачать:
| Вложение | Размер |
|---|---|
| ispolzovanie_graficheskih_vozmozhnostey_excel.doc | 292 КБ |
Предварительный просмотр:
Использование графических возможностей Excel для решения математических задач
Возможности ЭТ Microsoft Excel весьма многогранны. Всем известно, что Excel является мощным вычислительным инструментом, позволяющим производить простые и сложные расчеты в различных областях человеческой деятельности: математике, физике, инженерных науках, экономике, технологии. Но помимо осуществления расчетов возможно применение ЭТ Excel и в других областях. Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
Построение графиков элементарных функций в Excel
Для построения графика функции в Excel прежде всего надо построить таблицу, в одну колонку которой занести значение аргумента функции, а в другую — значение функции при заданном значении аргумента.
Для этого в рабочем поле Excel в ячейках 1-й строки напечатаем наименование работы, во 2-ой строке – заголовок «Расчетная таблица», в 3-й – наименование колонок (столбцов) расчетной таблицы.
Начиная с ячейки А5 произведем формирование значение таблицы. Для этого необходимо в ячейку А5 ввести первое значение аргумента вычисляемой функции из заданного диапазона значений аргументов. В ячейку А6 введем второе значение аргумента, отличающееся от первого на заданный шаг изменения аргумента. Далее пометим эти ячейки и, ухватив указателем мыши квадратную точку в правом нижнем углу помеченной области ячеек, движением вниз по столбцу с нажатой левой кнопкой мыши рассчитаем значения аргумента с шагом, который вычислил Excel по указанным первым двум ячейкам (рис.1).
Пометив ячейку В5, вычисляем первое значении функции, используя Мастер формул, и если функция проста, то записываем формулу вручную. Запись формулы в ячейку вручную следует начать со знака «=» и закончить нажатием клавиши Enter. Затем, используя квадратную точку помеченной ячейки, копируем формулу в остальные ячейки.
Для построения графика заданной функции по построенной таким образом таблице необходимо воспользоваться Мастером диаграмм. Следуя указаниям Мастера, выбираем форму диаграммы Точечная.
Построение графика функции y=ax 2 +bx+c.
Построим график указанной функции при а-2, b=5, c=-10. Для построения графика функции будем изменять аргумент в диапазоне -5≤x≤2,5 с шагом 0,5.
Выполним последовательно все действия, описанные выше, сравнивая получаемый результат с рис.1.