|
неправильная дробь – дробь, у которой числитель больше знаменателя. правильная – та дробь, у которой, соответственно, числитель меньше знаменателя. неправильную дробь превратить в правильную никак нельзя, но зато ее можно представить в виде смешанного числа, состоящего из двух частей (одна часть будет целым числом, а другая – как раз правильной дробью). например 5/2=2+1/2 (только пишут дробь обычно сразу после целого числа без знака “плюс”) здесь нужно числитель неправильной дроби разделить на знаменатель. записываем целую часть от деления (в нашем случае 2). затем остаток от деления (то есть 1) записываем как числитель дроби, которую мы записываем рядом с двойкой. автор вопроса выбрал этот ответ лучшим
Mirra-Mi 8 лет назад Для того чтобы преобразовать неправильную дробь в правильную для начала необходимо сказать: -У неправильной дроби числитель (верхнее число в дроби) больше знаменателя ил равна ему; -У правильной дроби все наоборот. Процесс преобразования разберем на примере дроби 260/7: 1) Сначала делим 260 на 7, получаем число 37,14.. 2) Число 37 будет стоять впереди дроби как целое число 3) Теперь 37 * 7 = 259 4) От числителя отнимаем получившееся число 260 – 259 = 1 – это число и будет в числители нашей правильной дроби. 5) При записи новой дроби знаменатель остается неизменной. В данном случае это 7. Правильная дробь будет выглядит следующим образом:
Проверка преобразованной дроби: Целое число умножаем на знаменатель и прибавляем числитель 37 * 7 + 1 = 260.
Leather-Radish 8 лет назад Неправильной дробью называют такую дробь, у которой числитель больше знаменателя. Значит правильная дробь та, у которой числитель меньше знаменателя. Чтобы превратить неправильную дробь в правильную можно представить в виде десятичного числа. Например 17/8 можно записать так: 2,125. Или записать так: 2 1/8. Чтобы решить поставленную задачу, сначала нужно четко уяснить для себя, что такое правильная дробь, а что такое неправильная. Начнем с того, что утверждение верно далеко не для всех чисел на числовой оси. Пример числитель равен (-10), знаменатель равен (-4)
аналогичное утверждение верно также не всегда Пример числитель равен 2, знаменатель равен (-3)
Поэтому Неправильную дробь можно записать с помощью суммы целого числа и правильной дроби (смешанной дроби) и для этого нужно: разделить числитель на знаменатель, полученное целое число записать в целой части, остаток в числителе, знаменатель оставить без изменений Пример в числителе (-15), в знаменателе 2, минус вынесем за пределы дроби – (15/2), 15 разделим на 2, целое число 7 ставим в целую часть дроби, остаток от деления 1 запишем в числителе, а знаменатель 2 оставим без изменений.
Правильной дробью называется такая дробь, у которой знаменатель больше числителя. Это говорит о том, что эта дробь показывает какую-то часть целого. Например дробь 1/2 говорит о том что у нас есть половина например арбуза, а дробь 7/9 – что у нас осталось семь кусочков арбуза разрезанного на 9 частей. Две части кто-то съел. Если же дробь неправильная, то есть числитель больше знаменателя, то совершенно непонятно, какая у нас часть целого, но разрезанного арбуза и сколько еще целых арбузов в наличии. Поэтому приходится перевести неправильную дробь в правильную. при этом мы получим какое-то целое число и остаток – именно правильную дробь. Для перевода делим числитель на знаменатель в столбик. Пример: 7/4. Семь на четыре дает единицу и остаток 3/4. Вот мы и перевели дробь в правильную – ответ 1 и 3/4. Полина Липатова 8 лет назад Например 4 целых и три одиннадцатых, мы 4 умножаем на 11 и +3 , потом мы делим на 11 , получается 44 +3 и делим на 11 , и получим дробь 47/11 . Неправильная дробь это когда есть целое число например 5,10 , то есть пять целых и 10/100 , пять мы умножаем 100 и +10 , получается 10/500 . Так же если например 6,6 , тут проще , 6 умножаем на 6 и +6 получается 12/6 , сокращаем на два , получается шесть третьих, шесть третьих мы сокращаем на три получается две первых , два делим на один получается два. То есть 6,6 =2.
Leona-100 8 лет назад Из школьного курса математики мы знаем. что неправильная дробь представляет собой дробь у которой числитель больше, чем ее знаменатель. Чтобы перевести ее в правильную дробь, нужно числитель такой дроби разделить на ее знаменатель. Все очень просто, таким образом она станет правильной, либо десятичной дробью.
[пользователь заблокирован] 8 лет назад Перевести неправильную дробь в правильную можно путем деления числителя такой дроби на знаменатель – таким образом мы получим правильную дробь. По другому неправильную дробь можно записать в виде простого десятичного числа.
Про100 й 8 лет назад Неправильная дробь например: 9/5 выделим у нее целую часть это будет: 1 4/5 теперь она немного похоже на правильную только с целой частью это единица. Можно и превратить ее в десятичную дробь в нашем случае будет 1.8 Апрели 8 лет назад Правильной дробью принято считать такую, у которой знаменатель выше числителя. Для того чтобы неправильную дробь перевести в правильную, надо разделить числитель неправильной дроби на ее знаменатель, результатом будет число с остатком. Знаете ответ? |
При решении примеров, связанных с дробными выражениями, часто приходится выполнять упрощения и различные арифметические операции. Зная, как перевести неправильную дробь в правильную, можно узнать, сколько целых частей содержится в числе, тем самым сделать вычисление проще. Такое действие актуально и при умножении или делении смешанных выражений. Метод преобразования довольно прост и не требует заучивания каких-либо сложных формул.
Оглавление:
- Общие сведения
- Способ деления
- Классический метод
- Преобразование на математическом калькуляторе
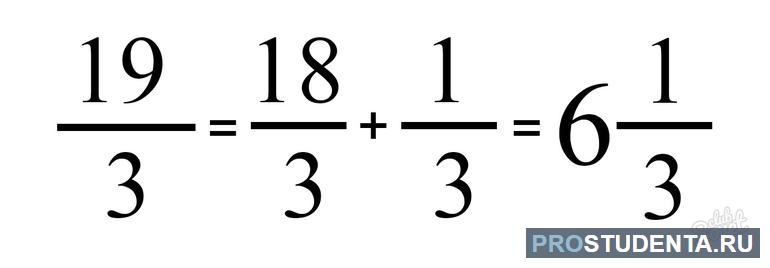
Общие сведения
При выполнении каких-либо математических расчётов часто приходится иметь дело с нецелыми числами. Одним из видов их записи является дробь. По сути, это отношение двух чисел. Пусть есть круг, разделённый на четыре равные части. Если в нём закрасить одну из них, то выполненное действие можно записать как ¼. То есть из целого выделили одну часть. Если закрасить два круга, то запись примет вид: 2/4. Фактически дробное выражение обозначает операцию обратную умножению, другими словами — деление.
Число, которое располагается слева, называют числителем. Он обозначает, сколько долей от целого была забрано. Поэтому его называют делимым. Число же, стоящее справа, называют знаменателем или делителем. Существует и другая форма записи — десятичная. В этом способе используют запятую, отделяя целую часть от десятичной. Например, ½ — это дробная запись, а 0,5 — десятичная. Причём эти две формы обозначения равнозначные. Так, если выполнить операцию деления, один разделить на два, то получится 0,5.
Существуют несколько типов дробей. По способу записи их разделяют на четыре вида:

- Правильные — дробные числа, у которых значение числителя меньше чем знаменателя: x/y, где x < y.
- Неправильные — дроби, в записи которых величина делимого превышает значение делителя: x/y, где x > y.
- Смешанные — выражения, состоящие из целого и дробного числа. По сути, такая дробь обозначает их сумму: Z (X/Y) = Z + (X/Y).
- Составные — содержат в записи несколько операций деления: (x/z)/y; (x/y)/(s/z).
Так как дроби — это способ записи чисел, то с ними можно выполнять любые математические действия. Например, складывать, вычитать, умножать, логарифмировать, возводить в степень и так далее. Причём для удобства выполнения операций часто приходится выполнять преобразования по переводу выражений из одного вида в другой.
Существуют специальные алгоритмы и правила, позволяющие как из неправильной дроби сделать правильную, так и преобразовать смешанное выражение.
Выполнение превращений относится к элементарным операциям и в ряде случаев позволяет значительно упростить решение примеров. Так, на первый взгляд, громоздкое выражение после преобразования становится простым и легко решаемым. При этом существуют и так называемые онлайн-калькуляторы. Это сервисы, выполняющие автоматический перевод из одного вида дроби в другой.
Способ деления

Любую неправильную дробь можно представить, как сумму натурального числа и правильного выражения. В отличие от записи, в которой числитель больше знаменателя, неправильное дробное выражение представляет собой число, которое больше либо равно единице. Одним из способов выполнить переход является простое деление. Выполнять его удобно с помощью метода «уголок».
Для этого сначала первую цифру числителя делят на знаменатель. Если результат действия не целое число, то операцию выполняют для двух первых знаков. То число, на которое числитель делится нацело, записывают под делителем. Это и будет значение целой доли. Затем определяют остаток. Вычисляют его по следующему алгоритму:
- умножают целое число на делитель;
- результат операции записывают под значением знаменателя;
- находят результат вычитания результата умножения из делимого.
Таким образом, первое число образует целую часть, второе записывают в числитель, а знаменатель оставляют без изменения. Например, 15/4. Так как 15 разделить на четыре без остатка нельзя, то подбирается ближайшее целое число. Им будет 12, так как 3 * 4 = 12. Если взять четыре, то при умножении получится 16, а это выражение уже превышает значение числителя. Затем из пятнадцати нужно вычесть двенадцать: 15 — 12 = 3. Все нужные вычисления выполнены, остаётся только записать правильно ответ: 3 (¾).
Вот ещё один пример. Преобразовать неправильную дробь: 78/32. По аналогии с предыдущим заданием превращение выполняют в два этапа. На первом находят целую составляющую, а на втором — дробную. Итак, ближайшее цело число к 78 при умножении на 32 будет 64: 32 * 2 = 64. Отсюда следует: 78 — 64 = 14. Значит, результат превращения будет иметь вид: 78/32 = 2 (14/32).
Как видно, ничего сложного в рассмотренном способе нет.
Главное — правильно подобрать число, на которое нацело делится числитель. Чаще всего им являются простые цифры. Но при этом, конечно же, всё зависит от конкретно рассматриваемого примера.
Классический метод
Этот способ считается классическим и обычно, если необходимо превратить неправильную дробь в выражение другого вида, используют его. Суть метода заключается в следующем. Пусть имеется неправильная дробь вида x/y, где икс превышает по значению игрек. Чтобы выполнить преобразование, нужно знать, что при делении числа само на себя получается единица. Например, 234/234 = 1, 6/6 = 1.
Используя это знание, исходную дробь нужно представить в виде суммы единицы и правильного выражения. Для этого в первом слагаемом в числителе пишут число, равняющееся знаменателю, то есть c/n = (n/n) + (?/n). Теперь нужно определить числитель во втором слагаемом.

По правилам сложения дробей с одинаковым знаменателем, при их суммировании последний остаётся без изменения, а над числителями выполняется нужное арифметическое действие. Таким образом, чтобы найти неизвестное, следует записать равенство: c/n = (n/n) + (?/n). Из правила сложения следует, что искомый числитель можно определить, как разницу между c и n. Теперь остаётся переписать исходную дробь как обычную смешанную: 1 ((c — n)/n).
Чтобы стало более понятно можно рассмотреть несколько конкретных примеров. Пусть нужно выполнить преобразование для дроби: 5/3. В соответствии с рассмотренным методом необходимо выражение представить в виде суммы: 3/3 + x/3. Теперь, чтобы найти неизвестное, следует из исходного числителя вычесть делимое, стоящее в первом слагаемом: 5 — 3 = 2. Значит, преобразование можно представить так: 5/3 = (3/3) + (2/3) = 1 + (2/3) = 1 (2/3).
Вот ещё один пример: 7/2 = (2/2) + (7 — 2)/2 = 1 + 5/2 = 1 + (2/2) + (3/2) = 1 + 1 + 2/2 + ½ = 3 (½). Как видно из второго примера, превратить дробь в неправильную не всегда получается в одно действие. В этом примере понадобилось три раза представлять выражение в виде суммы. Поэтому этот способ неудобно использовать при работе с длинными числами из-за большого числа выполняемых операций.

Следует отметить, что можно осуществлять и обратные действия, то есть переводить дробь в неправильную. Для этого целую часть нужно умножить на знаменатель дробной части, а после полученный результат сложить с числителем.
Полученная сумма будет являться числителем преобразованного выражения. Знаменатель же остаётся без изменения.
Например, 5 (4/7) = (5 * 7 + 4)/7 = 39/7.
Преобразование на математическом калькуляторе
Превращать неправильную дробь в правильную несложно. Но бывает так, что приходится иметь дело с большими числами. При этом преобразование может занять довольно длительное время. В таком случае хорошим выходом будет использовать математический калькулятор. Его принцип работы основан на алгоритмах превращения дроби из одного вида в другой. Это программа, занимающаяся расчётами, адаптирована под различные веб-браузеры и выполня ет вычисления в режиме реального времени.
Достоинства математических калькуляторов, умеющих преобразовывать дроби ещё и в том, что, кроме непосредственно результата действий, они выводят на экран подробное описание решения. Это помогает пользователю даже со слабой подготовкой научиться самостоятельно выполнять преобразования. Кроме этого, калькуляторы содержат необходимый минимум теоретической информации и даже примеры простых превращений. При этом они умеют выполнять и другие операции. Например, переводить смешанную дробь в неправильное число или выполнять какое-либо другое математическое действие.

Пользоваться математическими калькуляторами удобно будет как инженерам, которым необходимо быстро и правильно выполнить то или иное преобразование и учащимся.
Для первых это возможность не отвлекаться на расчёты и быть уверенным в правильности вычислений, а для вторых — подспорье в учёбе. Ведь с помощью такого калькулятора можно проверить самостоятельно полученный результат, а в случае необходимости найти и устранить ошибку.
Таким образом, чтобы преобразовать дробь можно применить два способа: классический и деления. Какой из них предпочтительно использовать зависит от конкретного примера. Но если вдруг перевод вызовет трудности, всегда можно воспользоваться программой для автоматического расчёта.
Как преобразовать неправильную дробь в правильную: шаг за шагом руководство
Неправильная дробь — это дробь, в которой числитель больше знаменателя. Примером такой дроби может быть 7/4 или 5/3. Преобразование неправильной дроби в правильную требует некоторых математических операций, но оно не сложно. В этой статье мы расскажем, как преобразовать неправильную дробь в правильную в несколько простых шагов.
Шаг 1. Деление числителя на знаменатель
Первым шагом необходимо разделить числитель на знаменатель неправильной дроби. Например, если у нас есть дробь 7/4, мы должны разделить 7 на 4. Результат этого деления будет равен 1 с остатком 3. Таким образом, мы получили правильную дробь 1 3/4.
Шаг 2. Упрощение правильной дроби
Вторым шагом необходимо упростить правильную дробь, полученную на предыдущем шаге. Для этого нужно найти наибольший общий делитель числителя и знаменателя, а затем разделить их на этот делитель. Например, если мы рассматриваем дробь 1 3/4, то наибольший общий делитель чисел 3 и 4 равен 1. Мы делим числитель и знаменатель на 1 и получаем упрощенную дробь 1 3/4.
Шаг 3. Проверка правильности упрощенной дроби
Третьим шагом необходимо проверить правильность упрощенной дроби. Для этого нужно убедиться, что числитель меньше знаменателя. Если это так, то мы получили правильную дробь. Если же числитель по-прежнему больше знаменателя, то мы должны повторить первый и второй шаги до тех пор, пока не получим правильную дробь.
Преобразование неправильной дроби в правильную, несмотря на то, что может показаться сложным на первый взгляд, на самом деле не требует никаких особенных знаний или навыков. Достаточно просто следовать приведенным выше шагам, чтобы получить правильную дробь из неправильной. Надеемся, что наша статья была полезна для вас!
Как перевести неправильную дробь в правильную


4.5
Средняя оценка: 4.5
Всего получено оценок: 408.
4.5
Средняя оценка: 4.5
Всего получено оценок: 408.
Как перевести неправильную дробь в правильную? Это невозможно. Объясним, почему так происходит и откуда берется желание сделать неправильную дробь правильной.
Что такое дробь?
Представим себе большую пиццу. Ее взяли и разрезали на кусочки компания друзей. Так вот, каждый кусочек представляет собой часть целого, верно? Так же и с дробью. Изначально дроби обозначали часть чего-то целого.
Знаменатель обозначал, на сколько кусочков разделили целое. Числитель говорит нам, сколько частей было принято для вычисления. Нас, как математиков, не особо волнует, куда делись остальные части.
Сегодня дробь – это число, которое можно назвать еще и незавершенной операцией деления. В любую минуту черту дроби можно заменить на знак деления, не нарушая математических законов.
Правильная дробь
Правильной дробь называют дробь, у которой числитель меньше знаменателя. Именно правильные дроби появились раньше всех прочих. Такими дробями были доли в пиратской добыче, пай в купеческих компаниях и части в крестьянских хозяйствах.
Правильной дробь зовут потому, что она соответствует понятию дроби людей Древнего мира. Дробью всегда обозначали часть целого, но сегодня дробь зачастую сильно превышают единицу. А правильные дроби соответствуют первоначальному значению, поэтому и зовутся именно так.
Неправильная дробь
Неправильная дробь это дробь, числитель которой больше знаменателя. Такая дробь больше единицы, поэтому и зовется неправильной. В счете неправильные дроби поддаются тем же правилам, что и правильные.
Перевести неправильную дробь в правильную невозможно. Это две разные категории чисел. Как нельзя перевести положительно число в отрицательное, потому что одно больше 0, а другое меньше.
Под переводом одного числа в другое подразумевается изменение записи числа без изменения реального значения. Для того, чтобы проверить не изменилось ли число в простой пример можно подставить сначала число до преобразования, а потом число после преобразования. Результат должен быть одинаковым.
Неправильную дробь можно перевести:
- В смешанное число
- В десятичную дробь
Смешанное число
Смешанным числом называют число, состоящее из двух части: дробной и целой. В неправильной дроби выделяют целую часть и получается подобное значение. Смешанные дроби нельзя перемножать и достаточно трудно складывать или вычитать.
Неправильную дробь в смешанное число переводят, только если все вычисления уже окончены и требуется красиво оформить результат. Для расчета смешанные дроби сначала переводят в неправильные дроби, выполняют вычисления и снова выделяют целую часть.

Что мы узнали?
Мы вспомнили, что такое правильная и неправильная дроби. Рассказали, почему числа получили такие названия. Сказали, что перевод неправильной дроби в правильную невозможен и объяснили, почему.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Кирилл Калинко
5/5
-

Нина Кононова
5/5
-

I–Саша ПАВЛЕНКО
5/5
-

Марина Туровец
5/5
-

Фёдор Худайгулов
5/5
-

Анжелика Афраилова
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 408.
А какая ваша оценка?


Как перевести неправильную дробь в правильную
Нехитрые математические правила и приемы, если они не используются постоянно, забываются быстрее всего. Еще быстрее уходят из памяти термины.
Одно из таких простых действий – преобразование неправильной дроби в правильную или, по-другому – смешанную.
1
Неправильная дробь
Неправильной называется дробь, у которой числитель (число над дробной чертой) больше или равно знаменателю (число под чертой). Такая дробь получается при сложении дробей или умножении дроби на целое число. По правилам математики такую дробь обязательно нужно превратить в правильную.
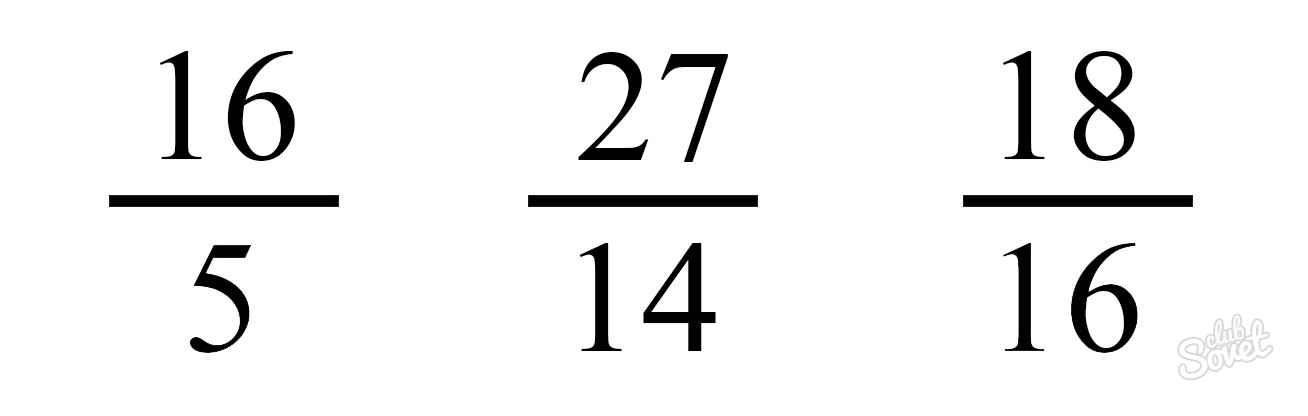
2
Правильная дробь
Логично предположить, что правильными называются все остальные дроби. Строгое определение – правильной называется дробь, у которой числитель меньше знаменателя. Дробь, у которой есть целая часть иногда называется смешанной.
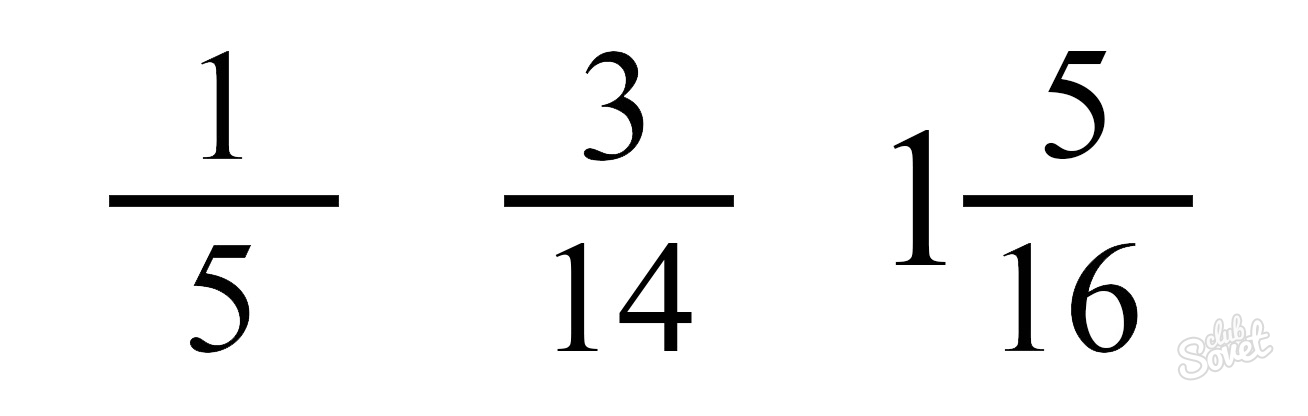
3
Преобразование неправильной дроби в правильную
- Первый случай: числитель и знаменатель равны друг другу. В результате преобразования любой такой дроби получится единица. Неважно, три третьих это или сто двадцать пять сто двадцать пятых. По сути, такая дробь обозначает действие деления числа на само себя.
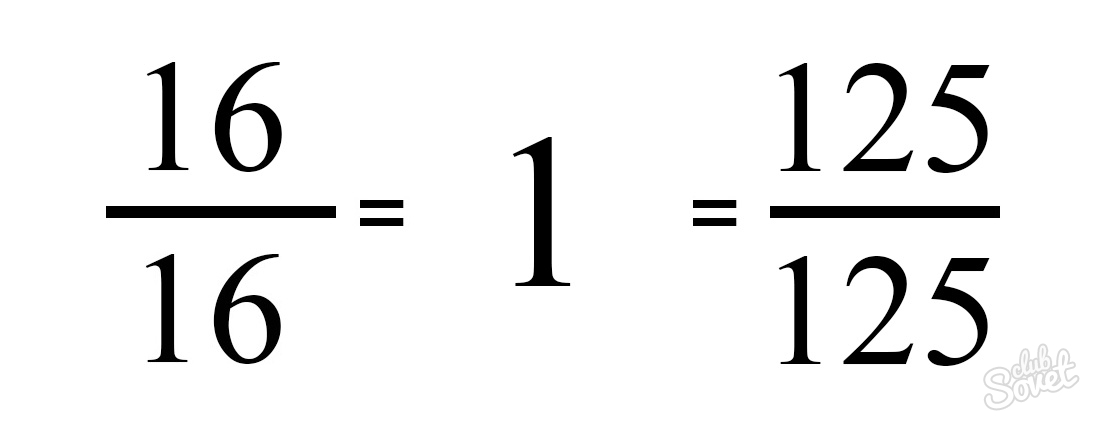
- Второй случай: числитель больше знаменателя. Здесь нужно вспомнить метод деления чисел с остатком.
Для этого нужно найти самое близкое к значению числителя число, которое делится на знаменатель без остатка. Например, у вас есть дробь девятнадцать третьих. Наиболее близкое число, которое можно разделить на три – это восемнадцать. Получится шесть. Теперь отнимите от числителя полученное число. Получим единицу. Это и есть остаток. Запишите результат преобразования: шесть целых и одна треть.
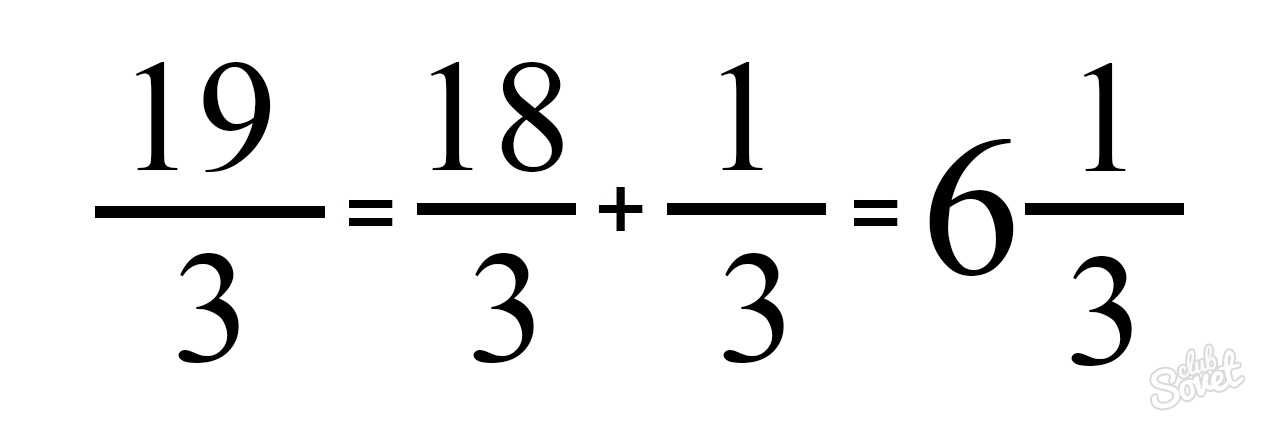
Но прежде чем приводить дробь к правильному виду, нужно проверить, можно ли её сократить.
Сокращение дроби возможно, если у числителя и знаменателя есть общий делитель. То есть такое число, на которое и то, и другое делится без остатка. Если таких делителей несколько, нужно найти наибольший.
Например, у всех четных чисел такой общий делитель – двойка. А у дроби шестнадцатых двенадцатых, есть еще один общий делитель – четверка. Это наибольший делитель. Разделите числитель и знаменатель на четыре. Результат сокращения: четыре третьих. А теперь, в качестве тренировки, преобразуйте эту дробь в правильную.







