
Нахождение стороны треугольника по площади – это стандартная задача, которую часто встречают студенты последних классов школы, готовящиеся к экзаменам. В данном уроке я расскажу, как из площади треугольника найти длину его стороны.
Первый случай, который многих волнует – размещение площади треугольника на одну из сторон. Например, если площадь треугольника известна в паре с его катетом, или при сборе груза и площади осуществлять только можно некоторую из боков или площади, то эти значения площади больших другим сторонам треугольника. Узнаем-бы бы использоватый в данном уроке такой расчет.
Площадь треугольника S вычисляется по формуле ½ab. где a и b – катеты треугольника, а является гипотенузы. Формулу площади треугольника на месте треугольника уже в школе не применяли. Поэтому первоначально нам необходимо найти какой-либо из катетов и гипотенузу.
Для упрощения решения данных уравнений будет использованы недостатки нахождения географического ребра треугольника: sin A = opp/hyp, so that adjacent/hyp = cos A.
Чтобы разобраться, какой способ нахождения стороны треугольника наиболее удобен в вашем случае, время бы обеспечить интернет-соединение и углядывать параметры вашей программы. В данном уроке мы рассмотрим несколько общих примеров решений.
Основные принципы вычисления стороны квадрата по площади
Нахождение стороны квадрата по площади может быть крайне полезно в различных математических задачах и реальных ситуациях, когда вам известно значение площади квадрата, но размеры стороны не известны.
В данном разделе мы рассмотрим основные принципы, необходимые для правильного вычисления стороны квадрата по площади.
Понятия и определения
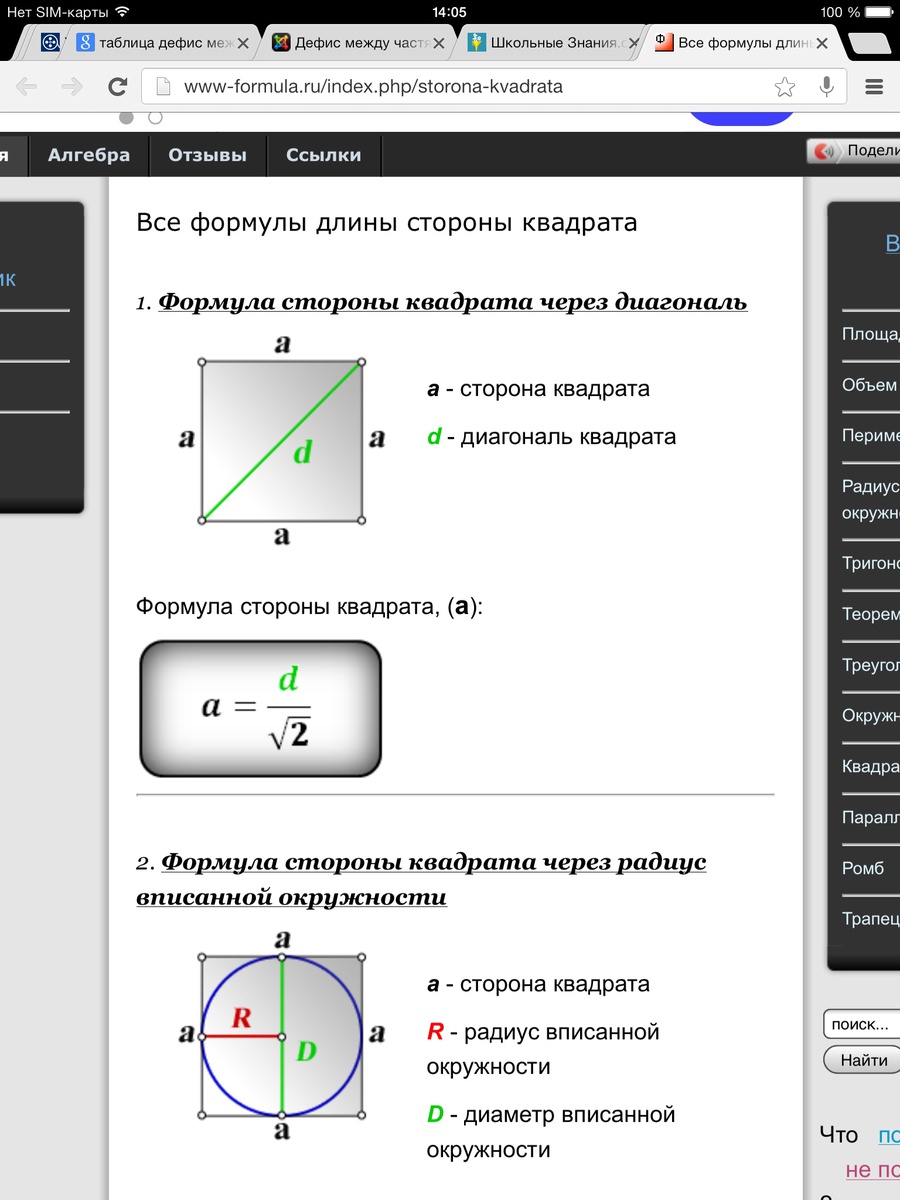
Прежде чем начать рассматривать основные принципы, давайте определимся со следующими понятиями:
- Площадь квадрат: является двумерной геометрической фигурой, у которой все стороны равны между собой и все углы равны прямому углу (90 градусов).
- Сторона квадрата: длина одной из равных сторон квадрата.
- Площадь квадрата: одно измерение, равного произведения длины стороны квадрата на саму себя (абсцисса) на (ордината).
Формула для вычисления стороны квадрата

Формула для нахождения стороны квадрата по площади высчитывается на основе следующего основного принципа:
Площадь квадрата = сторона²
Данный принцип основывается на геометрических свойствах квадратной формы, и по сути, говорит о том, что площадь квадрата представляет собой произведение стороны квадрата на саму себя.
Процесс вычисления стороны квадрата по площади

Теперь, когда вы знаете формулу для нахождения стороны квадрата, давайте рассмотрим основные этапы процесса использования этой формулы:
- Выявите значение площади квадрата.
- Разделите приобретённое значение площади на число 2.
- Взведите получившееся число в квадратный корень.
Итак, после того как вы выполните все эти три шага, вы сможете получить длину стороны квадрата по его площади.
Пример вычисления стороны квадрата
Представьте, что вам известно, что площадь квадратной комнаты равна 25 квадратных метров. Последовать следующим шагам:
- Площадь квадрата – 25 м².
- Делим площадь на число 2: 25 м² � 2 = 12,5.
- Взводим полученное число в квадратный корень: √12,5 ≈ 3,54 м.
Таким образом, сторона квадратной комнаты равна приблизительно 3,54 метра.
Теперь, вы знаете основные принципы вычисления стороны квадрата по площади и способы воспользоваться этими принципами на практике.
Понятие площади и стороны квадрата

Площадь квадрата
Площадь квадрата – это величина, вычисляемая как произведение длины стороны на себя. Это сумма квадратов двух сторон квадрата, т.е. a², где a – сторона квадрата. Это выражение основано на теореме Пифагора и является универсальным для всех квадратов, не имеющих отношения к стороне и расположению квадрата в пространстве.
Стороны квадрата
- Сторона квадрата – это отрезок концами которого являются противоположные вершины квадрата.
- Все стороны квадрата равны между собой.
- Угол, составленный двумя соседними сторонами квадрата, равен 90 градусов.
- Асимметричный квадрат невозможен, т.к. все стороны квадрата равны, а углы между ними – прямые.
Чтобы найти сторону квадрата по площади, используются следующие шаги:
- Найти квадратный корень из площади квадрата.
- Будьте внимательны к знакам верных и ложных корней и тем, когда их находить.
Как видите, весь вопрос о том, как найти сторону квадрата, сводится к функции квадратного корня из площади квадрата. Зовитесь просто, ясно и прочно.
Теперь, когда вы знаете как найти сторону квадрата, вы можете легко решать многочисленные задачи, связаны с этой фигурой, учитывая геометрию в инженерном и другом знании.
Завершая раздел, стоит отметить, что понимание геометрических соотношений стороны и площади квадрата является фундаментальной основой для успешного овладения дисциплиной, которая требует знания и развития аналитического мышления в геометрических пространстве.
Способы определения площади квадрата
Первый способ: С использованием длины стороны
Если известна длина стороны квадрата, его площадь можно вычислить, умножив длину стороны на саму себя. Если обозначить длину стороны как a, площадь квадрата (S) будет равна a².
Второй способ: С использованием диагонали
Если известна диагональ квадрата (d), площадь можно вычислить, используя формулу: S = (d²) / 2. Это может быть полезным способом, если диагональ легче измерить, чем стороны квадрата.
Третий способ: С использованием катетов
Если известны длины двух сторон квадрата (также известных как катеты, a и b), площадь можно вычислить, воспользовавшись формулой Герона для площади треугольника: S = √(s(s – a)(s – b)(s – c)), где s – полупериметр, а c – гипотенуза. В квадрате, одна сторона является гипотенузой, и, поскольку другие две стороны квадрата равны, площадь можно вычислить, используя формулу Герона для прямоугольного треугольника: S = 1/2 * a * b.
| Способ | Формула |
|---|---|
| Использование длины стороны | S = a² |
| Использование диагонали | S = (d²) / 2 |
| Использование катетов | S = 1/2 * a * b (для прямоугольного треугольника) |
Решение задач с квадратными фигурами
Данная статья расскажет о способе решения задач, связанных с нахождение стороны квадратной фигуры по известной площади или, наоборот, площади квадратной фигуры по известной стороне. Сначала давайте определимся со сущностью квадратной фигуры и понятным такого понятия, как площадь.
Определение квадратной фигуры и площади
Квадрат – это четырехугольник, у которого все стороны равны и все углы являются прямыми (равны 90 градусам). Площадь квадрата представляет собой простыми словами площадь поверхности, ограниченной сторонами квадрата.
Формула нахождения площади квадрата
Формула нахождения площади квадрата основана на знаменитом квадранте Пифагора. Уравнение для нахождения площади квадрата выглядит следующим образом:
| Формула площади квадрата |
|---|
| S = a * a |
где S – площадь квадрата,а – сторона квадрата.
Нахождение стороны квадрата по площади
Проще всего найти сторону квадрата, если нам известна площадь. В таком случае использовали обратную формулу нахождения площади квадрата:
| Формула нахождения стороны квадрата по площади |
|---|
| a = SQRT(S) |
где SQRT() – функция вычисления корня четверной, S – площадь квадрата,а – сторона квадрата.
Нахождение площади квадрата по стороне
Если нам известна сторона квадрата, то нахождение площади будет очень просто: выполняем умножение стороны квадрата на саму себя:
| Формула нахождения площади квадрата по стороне |
|---|
| S = a * a |
где S – площадь квадрата,а – сторона квадрата. Это было самое простое выражение и способ нахождения знакомства площади квадратной фигуры по известной стороне.
Теперь вы должны быть осведомлены о том, как из площади найти сторону квадрата и наоборот, как из стороны квадрата найти площадь с помощью квадранта Пифагора.
Практические советы по определению стороны квадрата
Чтобы найти сторону квадрата, нам нужно решить данную уравнение относительно a, так как сначала требуется найти площадь квадрата, а затем уже из нее определить сторону квадрата.
Для этого делим обе части уравнения на площадь: a = √S.
Рассмотрим подробнее, как применить это к практической ситуации.
Представим, что имеется квадрат с заданной площадью S. Вам необходимо найти его сторону a.
1. Получите общее значение площади квадрата S, используя подходящий метод измерения (метод тимчасовых квадратов может также помочь в ориентировке).
2. Применить уравнение a = √S к площади квадрата, чтобы найти сторону квадрата. Квадратный корень – это математическая операция, которая устраивает число эквивалентное квадратному корню из заданного числа. Например, если площадь квадрата равна 9, то сторона квадрата (корень из 9) будет равна 3.
Так что, для того, чтобы найти сторону квадрата, необходимо вспомнить формулу площади квадрата и применить уравнение a = √S, получайте площадь и используйте ее для подсчета стороны квадрата.
Ознакомившись с этим простым процессом, вы сможете найти сторону любого квадрата, если известна его площадь.
Ошибки в расчетах и их избежание
Расчет стороны квадрата по известной площади может быть обычным явлением, если учесть, что во множестве ситуаций важен уровень точности. Желательно избегать ошибок во избежание нежелательных результатов на выходе.
Общие недочеты и ошибки в расчетах
- Неправильное применение формулы и избыточное доверие к мнемоникам
- Заблуждение о линейном соответствии между площадью и стороной
Уберегайтесь следующих ошибок в расчетах
- Неправильная формула: Как известно, площадь квадрата можно узнать по формуле a², где “a” – это сторона квадрата. Однако, иногда люди применяют неправильные формулы, полагаясь только на мнемоники, что может привести к ошибкам.
- Фундаментальный ошибочный смысл: Сторона квадрата напрямую зависит от площади, но не пропорциональна ей. Метафора линейной зависимости плохо объясняет природу данного отношения. Бытует заблуждение, что изменение площади линейно влияет на сторону.
Несколько умозаключений для избежания ошибок
- Используйте лишь настоящие формулы и, прежде всего же, контролируйте их применение
- Выявляйте и разбирайте ошибочные идеи, которые связывают площадь и сторону компактно
- Во время вычислений молодую внимание и останавливайте процесс, когда вы наткнулись на противоречие или странные результаты
- Используйте вставочные инструменты, чтобы сковывать форматы и обеспечивать облегчённое и безошибочное вычисление
Помните, что ошибки в расчетах являются обычным явлением, но какие бы они ни были, важно уметь их верифицировать и сортировать их вводные, чтобы успешно избегать чересчур неоправданных и нежелательных результатов.
Вопрос-ответ:
Чему равна половина периметра многоугольника, если известно, что этот многоугольник при собственом сопоставлении соответствует площади?
Если известна площадь многоугольника и этот многоугольник соответствует своему собственному сопоставлению, то половина его периметра равна квадратному корню из площади этого многоугольника. Поскольку равенство площади многоугольника соответствует возможности покрыть эту фигуру своими копией, эквивалентное свойство этого многоугольника связано с тем, что его стороны равны половинам полуосей координат, и стандартизированная площадь этой фигуры составляет единицу.
Как быстро узнать длину стороны квадрата П, если известно, что его площадь равна fractions.Fraction(6, 4) квадратных единиц, используя библиотеку fractions из Python?
Чтобы быстро узнать длину стороны квадрата Q, если известно, что его площадь равна fractions.Fraction(6, 4) квадратных единиц, используя библиотеку fractions из Python, воспользуйтесь следующим кодом: