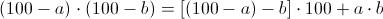Как легко найти число в квадрате

Когда надо найти квадрат какого-то двузначного числа, то в приницпе не так уж и сложно умножить его само на себя столбиком. Но что если надо найти много квадратов? Например, все квадраты чисел от 70 до 80? В этом случае умножать столбиком 11 раз будет не очень удобно. А если нужно найти квадраты чисел от 20 до 99, например?

В общем, показываю алгоритм, по которому все это находится буквально за секунды.

1. Нужно найти квадраты круглых чисел. В нашем случае квадраты 70 и 80 соответственно равны 4900 и 6400 — это легко. Плюс желательно вспомнить квадрат 75. У меня есть отдельная статья о том, как возводить в квадрат числа, заканчивающиеся на 5, но если коротко, то в конце надо написать 25, а в начале записать произведение 7•(7+1)=56. То есть 75²=5625. На картинке ниже изобразил схематично.

2. Дальше действуем по алгоритму. Числа 71 и 72 находятся ближе к 70, 73, 74, 76 и 77 ближе к 75, а 78 и 79 — к 80. На это мы будем опираться при вычислениях. Сейчас всё поймете. Чтобы считать быстрее, рекомендую прочитать мою статью о способах быстрого сложения и вычитания больших числе в уме.

71²=70²+70+71=4900+70+71=5041.

По такому же алгоритму считаем 76, но опираться будет не на 70, а на 75:

76²=75²+75+76=5625+75+76=5776.

С 74 и 79 почти точно так же, только мы не складываем, а отнимаем, так эти числа стоят слева от опорных 75 и 80.

74²=75²-75-74=5625-75-74=5550-74=5476.

79²=80²-80-79=6900-80-79=6320-79=6241.

3. Числа, которые стоят через одно от опорного, считаются чуть-чуть по-другому.

72²=70²+4•71=4900+284=5184

77²=75²+4•76=5625+304=5929

В числах, которые левее опорных, делаем вычитание вместо сложения:

73²=75²-4•74=5625-280-16=5329

78²=80²-4•79=640-320+4=6084.

На первый взгляд кажется сложно и громоздко, но стоит один раз понять, освоить и попробовать, как все сразу становится на свои места, и вы буквально за секунды сможете находить квадраты двухзначных чисел, немного потренировавшись и запомнив алгоритм.

Для простоты, постарался записать для вас алгоритм действий на одном листе. Сохраните картинку или лайкните этот пост. Можно будет поражать всех своим умением быстро считать в уме.

Напоминаю, тем кто ещё не подписался, что у меня появился одноименный канал на Ютубе, где я делюсь решениями интересных задач и всякими математическими и физическими хитростями.

Ещё интересно: Два простых способа быстрого сложения и вычитания в уме

90% европейских выпускников не смогли решить задачу, которую решили российские восьмиклассники

Простой и очень быстрый способ возведения в квадрат чисел, оканчивающихся на 5

Did this article help you?

Быстрое возведение чисел в квадрат без калькулятора

21 сентября 2013

Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.

Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:

[{{34}^{2}}=times frac{34}{frac{34}{+frac{136}{frac{102}{1156}}}}]

1156 — это и есть квадрат 34.

Проблему данного способа можно описать двумя пунктами:

1) он требует письменного оформления;

2) в процессе вычисления очень легко допустить ошибку.

Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.

Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:

[{{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]

[{{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}]

Что нам это дает? Дело в том, что любое значение в пределах от 10 до 100 представимо в виде числа $a$, которое делится на 10, и числа $b$, которое является остатком от деления на 10.

Например, 28 можно представить в следующем виде:

[begin{align}& {{28}^{2}} \& 20+8 \& 30-2 \end{align}]

Аналогично представляем оставшиеся примеры:

[begin{align}& {{51}^{2}} \& 50+1 \& 60-9 \end{align}]

[begin{align}& {{42}^{2}} \& 40+2 \& 50-8 \end{align}]

[begin{align}& {{42}^{2}} \& 40+2 \& 50-8 \end{align}]

[begin{align}& {{77}^{2}} \& 70+7 \& 80-3 \end{align}]

[begin{align}& {{21}^{2}} \& 20+1 \& 30-9 \end{align}]

[begin{align}& {{26}^{2}} \& 20+6 \& 30-4 \end{align}]

[begin{align}& {{39}^{2}} \& 30+9 \& 40-1 \end{align}]

[begin{align}& {{81}^{2}} \& 80+1 \& 90-9 \end{align}]

Что дает нам такое представление? Дело в том, что при сумме или разности, мы можем применить вышеописанные выкладки. Разумеется, чтобы сократить вычисления, для каждого из элементов следует выбрать выражение с наименьшим вторым слагаемым. Например, из вариантов $20+8$ и $30-2$ следует выбрать вариант $30-2$.

Аналогично выбираем варианты и для остальных примеров:

[begin{align}& {{28}^{2}} \& 30-2 \end{align}]

[begin{align}& {{51}^{2}} \& 50+1 \end{align}]

[begin{align}& {{42}^{2}} \& 40+2 \end{align}]

[begin{align}& {{77}^{2}} \& 80-3 \end{align}]

[begin{align}& {{21}^{2}} \& 20+1 \end{align}]

[begin{align}& {{26}^{2}} \& 30-4 \end{align}]

[begin{align}& {{39}^{2}} \& 40-1 \end{align}]

[begin{align}& {{81}^{2}} \& 80+1 \end{align}]

Почему следует стремиться к уменьшению второго слагаемого при быстром умножении? Все дело в исходных выкладках квадрата суммы и разности. Дело в том, что слагаемое $2ab$ с плюсом или с минусом труднее всего считается при решении настоящих задач. И если множитель $a$, кратный 10, всегда перемножается легко, то вот с множителем $b$, который является числом в пределах от одного до десяти, у многих учеников регулярно возникают затруднения.

Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:

[{{28}^{2}}={{(30-2)}^{2}}=200-120+4=784]

[{{51}^{2}}={{(50+1)}^{2}}=2500+100+1=2601]

[{{42}^{2}}={{(40+2)}^{2}}=1600+160+4=1764]

[{{77}^{2}}={{(80-3)}^{2}}=6400-480+9=5929]

[{{21}^{2}}={{(20+1)}^{2}}=400+40+1=441]

[{{26}^{2}}={{(30-4)}^{2}}=900-240+16=676]

[{{39}^{2}}={{(40-1)}^{2}}=1600-80+1=1521]

[{{81}^{2}}={{(80+1)}^{2}}=6400+160+1=6561]

Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.

Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.

Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:

[{{50}^{2}}=2500]

Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:

[{{51}^{2}}=2500+50+51=2601]

И так со всеми числами, отличающимися на единицу.

Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:

[{{21}^{2}}=400+20+21=441]

[{{39}^{2}}=1600-40-39=1521]

[{{81}^{2}}=6400+80+81=6561]

Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:

[begin{align}& {{26}^{2}}=625+25+26=676 \& 26=25+1 \end{align}]

При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.

Ключевые моменты

С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!

Для начала запомните квадраты значений, кратных 10:

[begin{align}& {{10}^{2}}=100,{{20}^{2}}=400,{{30}^{2}}=900,…, \& {{80}^{2}}=6400,{{90}^{2}}=8100. \end{align}]

Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:

[begin{align}& {{34}^{2}}={{(30+4)}^{2}}={{30}^{2}}+2cdot 30cdot 4+{{4}^{2}}= \& =900+240+16=1156; \end{align}]

[begin{align}& {{27}^{2}}={{(30-3)}^{2}}={{30}^{2}}-2cdot 30cdot 3+{{3}^{2}}= \& =900-180+9=729. \end{align}]

Как считать еще быстрее

Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:

[begin{align}& {{14}^{2}}={{15}^{2}}-14-15= \& =225-29=196. \end{align}]

Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:

[begin{align}& {{31}^{2}}={{30}^{2}}+30+31= \& =900+61=961. \end{align}]

Почему так происходит? Давайте запишем формулу квадрата суммы (и разности). Пусть $n$ — наше опорное значение. Тогда они считаются так:

[begin{align}& {{(n-1)}^{2}}=(n-1)(n-1)= \& =(n-1)cdot n-(n-1)= \& =={{n}^{2}}-n-(n-1) \end{align}]

— это и есть формула.

[begin{align}& {{(n+1)}^{2}}=(n+1)(n+1)= \& =(n+1)cdot n+(n+1)= \& ={{n}^{2}}+n+(n+1) \end{align}]

— аналогичная формула для чисел, больших на 1.

Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!

Смотрите также:

1. Решение ЕГЭ-2011: вариант 1, часть B
2. Задача B1 — время, числа и проценты
3. Комбинаторика в задаче B6: легкий тест
4. Интегрирование по частям
5. Нестандартная задача B2: студенты, гонорары и налоги
6. Особенности решения неравенств с радикалами

Время на прочтение
3 мин

Количество просмотров 114K

Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

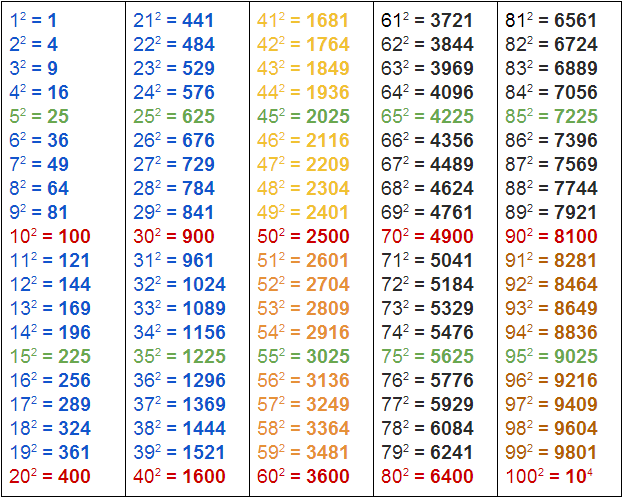
*квадраты до сотни

Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.

Правило 1 (отсекает 10 чисел)

Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.

70 * 70 = 4900.

В таблице отмечены красным.

Правило 2 (отсекает 10 чисел)

Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.

75 * 75 = 7 * 8 = 56 … 25 = 5625.

В таблице отмечены зеленым.

Правило 3 (отсекает 8 чисел)

Для чисел от 40 до 50.

XX * XX = 1500 + 100 * вторую цифру + (10 - вторая цифра)^2

Достаточно трудно, верно? Давайте разберем пример:

43 * 43 = 1500 + 100 * 3 + (10 - 3)^2 = 1500 + 300 + 49 = 1849.

В таблице отмечены светло-оранжевым.

Правило 4 (отсекает 8 чисел)

Для чисел от 50 до 60.

XX * XX = 2500 + 100 * вторую цифру + (вторая цифра)^2

Тоже достаточно трудно для восприятия. Давайте разберем пример:

53 * 53 = 2500 + 100 * 3 + 3^2 = 2500 + 300 + 9 = 2809.

В таблице отмечены темно-оранжевым.

Правило 5 (отсекает 8 чисел)

Для чисел от 90 до 100.

XX * XX = 8000+ 200 * вторую цифру + (10 - вторая цифра)^2

Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:

93 * 93 = 8000 + 200 * 3 + (10 - 3)^2 = 8000 + 600 + 49 = 8649.

В таблице отмечены темно-темно-оранжевым.

Правило №6 (отсекает 32 числа)

Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.

Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:

Формулы (осталось 24 числа)

Для чисел от 25 до 50

XX * XX = 100(XX - 25) + (50 - XX)^2

Например:

37 * 37 = 100(37 - 25) + (50 - 37)^2 = 1200 + 169 = 1369

Для чисел от 50 до 100

XX * XX = 200(XX - 50) + (100 - XX)^2

Например:

67 * 67 = 200(67 - 50) + (100 - 67)^2 = 3400 + 1089 = 4489

Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):

(a+b)^2 = a^2 + 2ab + b^2.
56^2 = 50^2 + 2*50*6 + 6*2 = 2500 + 600 + 36 = 3136. 

UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:

Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».

Для квадратов, соответственно, еще проще.

92*92 = (92-8)*100+8*8 = 8464

(от sielover)

Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.

Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.

Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.

Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

Как найти квадрат числа

Учитель на уроке диктует математическое выражение для того, чтобы учащиеся записали его в тетрадь: «Три в квадрате минус пять…» Один ученик не успевая, просит: «Подождите, не говорите слишком быстро, я еще квадрат не нарисовал». Так вот, дабы не рисовать квадраты и кубы на математике, нужно знать, что квадратом числа является его вторая степень, то есть когда число умножается на себя два раза. Вычислять квадраты учат в еще школе: дважды два – четыре, пятью пять – двадцать пять.

Вам понадобится

• – таблицы умножения;
• – таблица квадратов двузначных чисел;
• – калькулятор.

Инструкция

Чтобы найти квадрат любого числа достаточно только это число умножить на себя. Пример 1. 6*6 =36; 4*4 = 16; 7*7 = 49. Произведение чисел до 10, состоящих из одной цифры, размещено в таблице, знакомой всем еще с начальной школы: таблицы умножения. В ней по диагонали можно увидеть квадраты чисел: 1*1=1, 2*2=4, 3*3=9,4*4=16,5*5=25,6*6=36,7*7=49,8*8=64,9*9=81.

Вторая степень двузначных чисел (например, числа 16, 79, 54) определяется тем же способом: умножением числа на себя. Пример2. 20*20=400; 25*25=625; 40*40=1600. Существует специальная таблица квадратов двузначных чисел, размещенная в учебнике по алгебре для седьмого класса. В ней легко найти квадрат любого числа. Для этого разбейте число, возводимое в квадрат на десятки и единицы. Найдите пересечение строки-десятков и столбца-единиц по указанной таблице – ячейка на пересечении и будет содержать квадрат данного числа.

Если под рукой нет таблицы, квадрат числа можно найти произведением числа на само себя, выполненное в столбик. Этим способом находится и квадрат числа, состоящего из любого количества цифр. Однако квадрат большого числа лучше вычислить с помощью калькулятора. Для этого умножьте на нем заданное число само на себя. Сначала наберите нужное число с помощью цифровой клавиатуры, затем нажмите кнопку “*”. После этого еще раз наберите это же число и в заключении кнопку “=”. Калькулятор представит на экране точный ответ квадрата числа.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?