Метод интегрирования по частям используется тогда, когда нужно упростить имеющийся неопределенный интеграл или свести его к табличному значению. Чаще всего он применяется в случае наличия показательных, логарифмических, прямых и обратных тригонометрических формул и их сочетаний в подынтегральном выражении.
Основная формула, необходимая для использования этого метода, выглядит так:
∫f(x)dx=∫u(x)d(v(x))=u(x)v(x)-∫v(x)d(u(x))
Она означает, что нам нужно сначала представить выражение под интегралом в качестве произведения функции u(x) и дифференциала функции v(x). После этого мы вычисляем значение функции v(x) каким-либо методом (чаще всего применяется метод непосредственного интегрирования), а полученные выражения подставляем в указанную формулу, сводя исходный интеграл к разности u(x)v(x)-∫v(x)d(u(x)). Полученный в итоге интеграл также можно взять, используя любой метод интегрирования.
Рассмотрим задачу, в которой нужно найти множество первообразных функции логарифма.
Вычислите неопределенный интеграл ∫ln(x)dx.
Решение
Используем метод интегрирования по частям. Для этого берем ln(x) как функцию u(x), а остаток подынтегрального выражения – как d(v(x)). В итоге получаем, что ln(x)dx=u(x)d(v(x)), где u(x)=ln(x), d(v(x))=dx.
Дифференциалом функции u(x) является d(u(x))-u'(x)dx=dxx, а функция v(x) может быть представлена как v(x)=∫d(v(x))=∫dx=x
Важно: константа C при вычислении функции v(x) будет считаться равной 0.
Подставим то, что у нас получилось, в формулу интегрирования по частям:
∫ln(x)dx=u(x)v(x)-∫v(x)d(u(x))==ln(x)·x-∫x·dxx=ln(x)·x-∫dx=ln(x)·x-x+C1==x(ln(x)-1)+C
где C=-C1
Ответ: ∫ln(x)dx=x(ln(x)-1)+C.
Наиболее сложным в применении данного метода является выбор, какую именно часть исходного выражения под интегралом взять в качестве u(x), а какую – d(v(x)).
Разберем несколько стандартных случаев.
Если у нас в условии стоят интегралы вида ∫Pn(x)·eaxdx, ∫Pn(x)·sin(ax)dx либо ∫Pn(x)·cos(ax)dx, где a является коэффициентом, а Pn(x) – многочленом степени n, то в качестве функции u(x) нужно взять именно Pn(x).
Найдите множество первообразных функции f(x)=(x+1)·sin(2x).
Решение
Мы можем взять по частям неопределенный интеграл ∫(x+1)·sin(2x)dx. Берем x+1 в качестве u(x) и sin(2x)dx в качестве d(v(x)), то есть d(u(x)) = d(x+1) = dx.
Используя непосредственное интегрирование, получим:
v(x)=∫sin(2x)dx=-12cos(2x)
Подставляем в формулу интегрирования по частям:
∫(x+1)·sin(2x)dx=u(x)v(x)-∫v(x)d(u(x))==(x+1)·-12cos(2x)-∫-12cos(2x)dx==-12(x+1)·cos(2x)+12∫cos(2x)·d(x)==-12(x+1)·cos(2x)+14sin(2x)+C
Ответ: ∫(x+1)·sin(2x)dx=-12(x+1)·cos(2x)+14sin(2x)+C.
Вычислите неопределенный интеграл ∫(x2+2x)exdx.
Решение
Берем многочлен второго порядка x2+2x в качестве u(x) и d(v(x))-exdx.
∫x2+2xexdx=u(x)=x2+2x, d(v(x))=exdxd(u(x))=(2x+2)dx, v(x)=∫exdx=ex==u(x)v(x)-∫v(x)d(u(x))=(x2+2x)ex-∫(2x+2)exdx
К тому, что у нас получилось, надо опять применить метод интегрирования по частям:
∫(2x+2)exdx=(x2+2x)ex-∫2x+2exdx==u(x)=(2x+2), d(v(x))=exdxd(u(x))=2dx, v(x)=∫exdx=ex==(x2+2x)ex-(2x+2)ex-∫v(x)d(u(x))==(x2+2x)ex-(2x+2)ex-∫2exdx==(x2+2x-2x-2)ex+2∫exdx=(x2-2)ex+2ex+C=x2ex+C
Ответ: ∫(x2+2x)exdx=x2ex+C.
Вычислите интеграл ∫x3cos13xdx.
Решение
Согласно методу интегрирования по частям, берем u(x)=x3 и d(v(x))=cos13xdx.
В таком случае d(u(x))=3x2dx и v(x)=∫cos13xdx=3sin13x.
Теперь подставим полученные выражения в формулу:
∫x3cos13xdx=u(x)v(x)-∫v(x)d(u))==x33sin13x-∫3x23sin13xdx==3x3sin13x-9∫x2sin13xdx
У нас получился неопределенный интеграл, который опять же нужно взять по частям:
∫x3cos13xdx=3x3sin13x-9∫x2sin13xdx==u(x)=x2, d(v(x))=sin13xdxd(u(x))=2xdx, v(x)=∫sin13xdx=-3cos13x==3x3sin13x-9-3x2cos13x-∫-3cos13x·2xdx==3x3sin13x+27×2·cos13x-54∫xcos13xdx
Выполняем частичное интегрирование еще раз:
∫x3cos13xdx=3x3sin13x+27×2·cos13x-54∫xcos13xdx==u(x)=x, d(v(x))=cos13xdxd(u(x))=dx, v(x)=∫cos13xdx=3sin13x==3x3sin13x+27x2cos13x-543xsin13x-∫3sin13xdx==3×3-162xsin13x+27x2cos13x+162∫sin13xdx==(3×3-162x)sin13x+27x2cos13x-486cos13x+C==(3×3-162x)sin13x+(27×2-486)cos13x+C
Ответ: ∫x3cos13xdx=(3×3-162x)sin13x+(27×2-486)cos13x+C.
Если же у нас в условии стоят интегралы вида ∫Pn(x)·ln(ax)dx, ∫Pn(x)·arcsin(ax)dx,∫Pn(x)·arccos(ax)dx, ∫Pn(x)·arctg(ax)dx, ∫Pn(x)·arcctg(ax)dx
то нам следует брать в качестве u(x) функции arctg(ax), arcctg(x), ln(ax), arcsin(ax), arcos(ax).
Вычислите множество первообразных функции (x+1)ln(2x).
Решение
Принимаем ln(2x) в качестве u(x), а (x+1)dx – в качестве d(v(x)). Получаем:
d(u(x))=(ln(2x))’dx=12x(2x)’dx=dxxv(x)=∫(x+1)dx=x22+x
Подставим эти выражения в формулу:
∫(x+1)ln(2x)dx=u(x)v(x)-∫v(x)d(u(x))==x22+xln2x-∫x22+xdxx==x22+xln(2x)-∫x2+1dx=x22+xln2x-12∫xdx-∫dx==x22+xln(2x)-x24-x+C
Ответ: ∫(x+1)ln(2x)dx=x22+xln(2x)-x24-x+C.
Вычислите неопределенный интеграл ∫x·arcsin(2x)dx.
Решение
Решаем, какую часть взять за u(x), а какую – за d(v(x)). Согласно правилу, приведенному выше, в качестве первой функции нужно взять arcsin(2x), а d(v(x)) = xdx. Получим:
d(u(x))=(arcsin(2x)’dx=2x’dx1-(2x)2=2dx1-(2x)2, v(x)=∫xdx=x22
Подставляем значения в формулу:
∫x·arcsin(2x)dx=u(x)v(x)-∫v(x)d(u(x))==x22arcsin(2x)-∫x22-2dx1-(2x)2=x22arcsin(2x)-∫x2dx1-4×2
В итоге мы пришли к следующему равенству:
∫x·arcsin(2x)dx=x22arcsin(2x)-∫x2dx1-4×2
Теперь вычислим получившийся в итоге интеграл ∫x2dx1-4×2:
∫x2dx1-4×2=∫x2dx414-x2=12∫x2dx14-x2=-12∫-x2dx14-x2==-12∫14-x2-1414-x2dx=-1214-x2dx+18∫dx14-x2==-12∫14-x2dx+18arcsin(2x)
Здесь можно применить метод интегрирования по частям и получить:
∫x2dx1-4×2=-12∫14-x2dx+18arcsin(2x)==u(x)=14-x2, d(v(x))=dxd(u(x))=14-x2’dx214-x2=-xdx14-x2, v(x)=∫dx=x==-12u(x)v(x)-∫v(x)d(u(x))+18arcsin(2x)==-12×14-x2-∫-x2dx14-x2+18arcsin(2x)==-12×14-x2-12∫x2dx14-x2+18arcsin(2x)==-12×14-x2-∫x2dx1-4×2+18arcsin(2x)
Теперь наше равенство выглядит так:
∫x2dx1-4×2=-12×14-x2-∫x2dx1-4×2+18arcsin(2x)
Мы видим, что интеграл справа аналогичен тому, что получился слева. Переносим его в другую часть и получаем:
2∫x2dx1-4×2=-12×14-x2+18arcsin(2x)+C1⇒x2dx1-4×2=-14×14-x2+116arcsin(2x)+C2x2dx1-4×2=-18×14-x2+116arcsin(2x)+C2
где C2=C12
Вернемся к исходным переменным:
∫x·arcsin(2x)dx=x22arcsin(2x)-∫x2dx1-4×2==x22arcsin(2x)–18×1-4×2+116arcsin(2x)+C2==12×2-18arcsin(2x)+18×1-4×2+C
где С=-С2
Ответ: ∫x·arcsin(2x)dx=12×2-18arcsin(2x)+18×1-4×2+C.
Если же у нас в задаче стоит интеграл вида ∫ea·x·sin(bx)dx либо ∫ea·x·cos(bx)dx, то в качестве u(x) может быть выбрана любая функция.
Вычислите неопределенный интеграл ∫ex·sin(2x)dx.
Решение
∫exsin(2x)dx=u(x)=sin(2x), d(v(x))=exdxd(u(x))=2cos(2x)dx, v(x)=∫exdx=ex==u(x)v(x)-∫v(x)d(u(x))=sin(2x)ex-∫ex·2cos2xdx==sin(2x)ex-2∫excos(2x)dx=u(x)=cos(2x), d(v(x))=exdxd(u(x))=-2sin(2x)dx, v(x)=∫exdx=ex==sin(2x)ex-2cos(2x)ex-∫(ex(-2sin(2x)dx))==sin(2x)ex=2cos(2x)ex-4∫exsin(2x)dx
В итоге у нас получится:
∫exsin(2x)dx=sin(2x)ex-2cos(2x)ex-4∫exsin(2x)dx
Мы видим одинаковые интегралы слева и справа, значит, можем привести подобные слагаемые:
5∫exsin(2x)dx=sin(2x)ex-2cos(2x)ex⇒∫exsin(2x)dx=15sin(2x)ex-25cos(2x)ex+C
Ответ: ∫exsin(2x)dx=15sin(2x)ex-25cos(2x)ex+C
Этот способ решения является стандартным, и справа нередко получается интеграл, который идентичен исходному.
Мы рассмотрели наиболее типовые задачи, в которых можно точно определить, какую часть выражения взять за d(v(x)), а какую за u(x). В остальных случаях это приходится определять самостоятельно.
Также советуем вам ознакомиться с материалом, посвященным основным методам интегрирования.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Интегрирование по частям
Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.
Формула для неопределенного интеграла:
$$ int udv = uv – int vdu $$
Формула для определенного интеграла:
$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} – int limits_{a}^{b} vdu $$
Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.
| Пример 1 |
| Найти интеграл $ int xe^xdx $ |
| Решение |
|
Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $ Подставляем найденные значения в первую формулу интегрирования и получаем $$ int xe^x dx = xe^x – int e^x dx = xe^x – e^x + C. $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ int xe^x dx = xe^x – e^x + C $$ |
| Пример 2 |
| Найти интеграл $ int xcos x dx $ |
| Решение |
|
В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $. Подставим функции $ u $ и $ v $ в первую формулу $$ int x cos x dx = x sin x – int sin x dx = x sin x + cos x + C. $$ |
| Ответ |
|
$$ int x cos x dx = x sin x + cos x + C $$ |
| Пример 3 |
| Вычислить интеграл $ int limits_1 ^e xln x dx $ |
| Решение |
|
В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения $$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$ Осталось подставить это в формулу $$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e – int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} – 0 – frac{1}{2} int limits_1 ^e xdx = $$ $$ =frac{e^2}{2} – frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} – frac{1}{2}(frac{e^2}{2} – frac{1}{2}) = frac{e^2}{2} – frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$ |
| Ответ |
|
$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$ |
| Пример 4 |
| Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $ |
| Решение |
|
По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет “на руку”. Поэтом поступаем так $$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$ Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу $$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 – int limits_0 ^1 frac{3^x dx}{ln 3} = $$ $$ = frac{18}{ln 3} – frac{5}{ln 3} – frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} – frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$ |
| Ответ |
| $$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$ |
Пусть
![]() и
и![]() – непрерывно дифференцируемые функции.
– непрерывно дифференцируемые функции.
На основании формулы дифференциала
произведения имеем
![]() .
.
Отсюда
![]() .
.
Интегрируя,
получим:
![]() или окончательно
или окончательно
|
|
(4) |
Формула (4) называется формулой
интегрирования по частям.
Выведенная формула показывает, что
интеграл
![]() приводится к интегралу
приводится к интегралу![]() ,
,
который может оказаться более простым,
чем исходный, или даже табличным. Сущность
метода интегрирования по частям вполне
соответствует его названию. Дело в том,
что при вычислении интеграла этим
методом подынтегральное выражение![]() представляется в виде произведения
представляется в виде произведения
множителейuиdv.
При этом dx обязательно входит в
dv. В результате получается, что заданный
интеграл находится по частям: сначала
находим![]() ,
,
а затем![]() .
.
Пример 1.
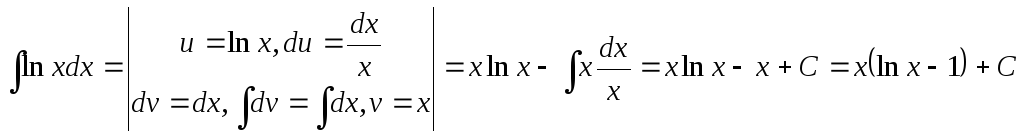 .
.
В представленном примере, как и в
дальнейших, вертикальными черточками
отделены вспомогательные записи. Отметим
также, что в качестве vможно взять любую функцию видаx+C,гдеС– постоянная. Мы взялиv=x,
т.е.С=0.
Пример
2.

![]() .
.
Пример
3.

![]() .
.
Пример 4.
 .
.
Иногда для вычисления
интеграла формулу интегрирования по
частям приходится применять несколько
раз.
Пример
5.
![]()
![]()
![]() .
.
Таким образом, интеграл
![]() вычислен двукратным интегрированием
вычислен двукратным интегрированием
по частям.
Пример 6.
![]()
![]() .
.
Если бы выражение
u
и dv
мы выбрали иначе, т.е.
![]() ,
,
то получили бы![]() ,
,
откуда![]() ,
,
и пришли бы к интегралу более сложному,
чем исходный, т.к. степень сомножителя
при тригонометрической функции повысилась
на единицу.
Приведенный пример показывает, что при
вычислении интегралов методом
интегрирования по частям главным
является разумное разбиение подынтегрального
выражения на множители uиdv. Общих установок
по этому вопросу не имеется. Однако, для
некоторых типов интегралов сделать это
возможно.
а) В интегралах вида
![]()
![]()
![]()
где
P(х)
– многочлен относительно x,
а –
некоторое число, полагают u=P(x),
а остальные сомножители за
![]() .
.
Пример 7.
Найти
![]() .
.
Положим
![]() ,
,![]() ,
,
тогда![]() ,
,![]() .
.
Следовательно,
![]()
б) В интегралах вида
![]()
![]()
![]()
![]()
![]()
полагают
![]() а
а
остальные сомножители – заu.
Пример 8.
Найти
![]() .
.
Следовательно,
![]() .
.
Вычислим отдельно последний интеграл:
![]() .
.
Итак,
![]() .
.
Отметим, что на
практике важно научиться применять
формулу (4), не выписывая по возможности
в стороне выражения для функций u
и v.
Так, решение приведенного примера может
быть представлено в виде:
![]()
=![]() .
.
Возвращение к исходному интегралу
Формула интегрирования
по частям применима и для нахождения
интегралов вида
![]() и
и![]() ,
,
гдеа
и b
– числа. При
нахождении этих интегралов она применяется
последовательно два раза, причем оба
раза за u
выбирается либо показательная функция,
либо тригонометрическая. После
двукратного интегрирования по частям
получается линейное уравнение относительно
искомого интеграла.
Пример 9.
Найти I
=![]() .
.
Положим
![]() ,
,![]() .
.
Тогда![]() ,
,![]() .
.
Следовательно,
I
=![]() .
.
Для вычисления
интеграла
![]() снова
снова
применим интегрирование по частям.
Положим![]() ,
,![]() .
.
Тогда![]() ,
,![]() .
.
Таким образом,
I=![]() =
=![]()
![]() .
.
Так как в правой части стоит искомый
интеграл, то, перенося его в левую часть,
получим:
![]() .
.
Отсюда получаем окончательный результат:
![]() =
=![]() .
.
Применим изложенный
метод к вычислению еще двух, часто
используемых в приложении, интегралов.
Пример
10. Найти
I
=![]() .
.
Положим
![]() ,
,![]() .
.
Тогда![]() ,
,![]() .
.
Следовательно,
|
|
(*) |
Так
как
![]() ,
,
то
![]()
(см.
лекция 2, п.2б, пример 20).
Подставив
полученное выражение в равенство (*),
будем иметь
![]() .
.
Таким
образом,
![]() .
.
Пример
11. Найти
![]() ,(а0)
,(а0)
Положим
![]() ,
,![]() ,
,
откуда![]() ,
,![]() .
.
Следовательно,
![]() ,
,
или
![]() .
.
Отсюда получаем:
![]() .
.
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 апреля 2020 года; проверки требуют 6 правок.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие равенства
- для неопределённого интеграла
или в другой записи
- для определённого интеграла
Предполагается, что нахождение интеграла 

Получение формул[править | править код]
Для неопределённого интеграла[править | править код]
Функции 

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:
Операция интегрирования обратна дифференцированию:
После перестановок:
Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.
Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:
Отсюда «следствие»: 
Для определённого интеграла[править | править код]
В целом аналогично случаю неопределённого интеграла:
Данные формулы справедливы, если каждая из функций 

Табличное интегрирование по частям[править | править код]
Основной процесс приведённой выше формулы может быть обобщено в таблице.
Например, рассмотрим интеграл
Начнем перечислять в столбце D функцию 



-
# i Знак D: производные u(i) I: интегралы v(n−i) 0 + 1 − 2 + 3 − 4 +
Произведение значений в ряду i столбцов D и I вместе с соответствующим им знаком выдают соответствующие интегралы на шаге i в течение повторяющихся шагов интегрирования по частям. Шаг i = 0 несет в себе исходный интеграл. для полного результата в шаге i > 0 i-й интеграл должен быть добавлен к предыдущим произведениям(0 ≤ j < i) j-го значения столбца D и (j + 1)-го значения столбца I (т.е., умножить 1-ое значение столбца D на 2-ое значение столбца I, 2-ое значение столбца D на 3-е значение столбца I, и т.д. …) не забывая о j-м знаке. Процесс завершается, когда произведение, которое несет в себе интеграл, принимает значение 0 (i = 4 в нашем примере). Конечный результат следующий: (включая разные знаки в каждом сегменте):
В итоге:
Примеры[править | править код]
- Данный метод также используется для нахождения интегралов от элементарных функций:
- В некоторых случаях интегрирование по частям не даёт прямого ответа:
- Таким образом один интеграл выражается через другой:
- Решив полученную систему, получаем:
Многомерный случай[править | править код]
Существует обобщение формулы интегрирования по частям для функций от нескольких переменных. В таком случае вместо интервала рассматривается подмножество 
Пусть 





где 




См. также[править | править код]
- Интеграл
- Интеграл Римана
- Преобразование Лежандра
- Методы интегрирования
- Дискретное преобразование Абеля — аналог интегрирования по частям для сумм.
Литература[править | править код]
- Маслов А. П., Белоус Е. А. Тема 5.2 // Математика для инженеров (2 курс).
- Тимофеев А. Ф. Интегрирование функций. — М.—Лен.: ОГИЗ, Гостехиздат, 1948. — С. 37—42.
Также см. Математический анализ#Библиография.
Ссылки[править | править код]
- Математика для заочников и не только. Дата обращения: 11 мая 2011.
- Канал СЗТУ на сайте youtube.com. Дата обращения: 11 мая 2011.
Содержание:
- Объяснение
- Примеры решения интегралов данным методом
Рассмотрим функции $u=u(x)$ и
$v=v(x)$, которые имеют непрерывные
производные.
Согласно свойствам дифференциалов, имеет место следующее равенство:
$d(u v)=u d v+v d u$
Проинтегрировав левую и правую части последнего равенства, получим:
$int d(u v)=int(u d v+v d u) Rightarrow u v=int u d v+int v d u$
Полученное равенство перепишем в виде:
$int u d v=u v-int v d u$
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл
$int u d v$ можно свести к нахождению интеграла
$int v d u$, который может быть более простым.
Замечание
В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
1) $int P_{n}(x) e^{k x} d x$ ;
$int P_{n}(x) sin (k x) d x$ ;
$int P_{n}(x) cos (k x) d x$
Здесь $P_{n}(x)$ – многочлен степени
$n$,
$k$ – некоторая константа. В данном случае в качестве
функции $u$ берется многочлен, а в качестве
$d v$ – оставшиеся сомножители. Для интегралов такого
типа формула интегрирования по частям применяется $n$ раз.
Примеры решения интегралов данным методом
Пример
Задание. Найти интеграл
$int(x+1) e^{2 x} d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.
$$int(x+1) e^{2 x} d x quadleft|begin{array}{cc}
u=x+1 & d v=e^{2 x} d x \
d u=d x & v=frac{1}{2} e^{2 x}
end{array}right|=(x+1) cdot frac{1}{2} e^{2 x}-int frac{1}{2} e^{2 x} d x=$$
$=frac{(x+1) e^{2 x}}{2}-frac{1}{2} int e^{2 x} d x=frac{(x+1) e^{2 x}}{2}-frac{1}{2} cdot frac{1}{2} e^{2 x}+C=$
$=frac{(x+1) e^{2 x}}{2}-frac{e^{2 x}}{4}+C$
Ответ. $int(x+1) e^{2 x} d x=frac{(x+1) e^{2 x}}{2}-frac{e^{2 x}}{4}+C$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти интеграл
$int x^{2} cos x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям. Для решения
данного интеграла эту операцию надо повторить 2 раза.
$$int x^{2} cos x d xleft|begin{array}{ll}
u=x^{2} & d v=cos x d x \
d u=2 x d x & v=sin x
end{array}right|=x^{2} sin x-int sin x cdot 2 x d x=$$
$$=x^{2} sin x-2 int x sin x d x | begin{array}{ll}
u=x & d v=sin x d x \
d u=d x & v=-cos x
end{array}$$
$=x^{2} sin x-2left(x cdot(-cos ) x-int(-cos x) d xright)=$
$=x^{2} sin x+2 x cos x-2 int cos x d x=$
$=x^{2} sin x+2 x cos x-2 sin x+C=left(x^{2}-1right) sin x+2 x cos x+C$
Ответ. $int x^{2} cos x d x=left(x^{2}-1right) sin x+2 x cos x+C$
2)$int P_{n}(x) arcsin x d x$ ;
$int P_{n}(x) arccos x d x$ ;
$int P_{n}(x) ln x d x$
Здесь принимают, что $d v=P_{n}(x) d x$, а в
качестве $u$ оставшиеся сомножители.
Пример
Задание. Найти интеграл
$int ln x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.
$$int ln x d xleft|begin{array}{l}
u=ln x quad d v=d x \
d u=frac{d x}{x} quad v=x
end{array} quadright|=x ln x-int x cdot frac{d x}{x}=$$
$=x ln x-int d x=x ln x-x+C=x(ln x-1)+C$
Ответ. $int ln x d x=x(ln x-1)+C$
Пример
Задание. Найти интеграл
$int arcsin x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям. Для решения
данного интеграла эту операцию надо повторить 2 раза.
$$int arcsin x d xleft|begin{array}{cc}
u=arcsin x & d v=d x \
d u=frac{d x}{sqrt{1-x^{2}}} & v=x
end{array}right|=$$
$$begin{array}{r||l||}
=x arcsin x-int frac{x d x}{sqrt{1-x^{2}}} & begin{array}{l}
1-x^{2}=t^{2} \
-2 x d x=2 t d t \
x d x=-t d t
end{array}
end{array}$$
$=x arcsin x-int frac{-t d t}{sqrt{t^{2}}}=x arcsin x+int frac{t d t}{t}=x arcsin x+int d t=$
$=x arcsin x+t+C=x arcsin x+sqrt{1-x^{2}}+C$
Ответ. $int arcsin x d x=x arcsin x+sqrt{1-x^{2}}+C$
3)$int e^{k x+b} sin (c x+f) d x$ ;
$int e^{k x+b} cos (c x+f) d x$
В данном случае в качество $u$ берется либо экспонента,
либо тригонометрическая функция. Единственным условием есть то, что при дальнейшем применении формулы интегрирования по частям в
качестве функции $u$ берется та же функция, то есть либо
экспонента, либо тригонометрическая функция соответственно.
Пример
Задание. Найти интеграл
$int e^{2 x+1} sin x d x$
Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям.
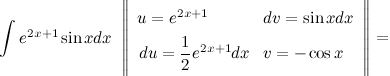
$=-e^{2 x+1} cos x-int(-cos x) cdot frac{e^{2 x+1}}{2} d x=$
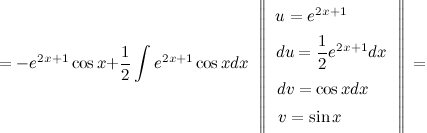
$=-e^{2 x+1} cos x+frac{1}{2}left(e^{2 x+1} sin x-int sin x cdot frac{e^{2 x+1}}{2} d xright)=$
$=-e^{2 x+1} cos x+frac{e^{2 x+1} sin x}{2}-frac{1}{4} int e^{2 x+1} sin x d x$
Таким образом, получили равенство:
$int e^{2 x+1} sin x d x=-e^{2 x+1} cos x+frac{e^{2 x+1} sin x}{2}-frac{1}{4} int e^{2 x+1} sin x d$
Перенося интеграл из правой части равенства в левую, имеем:
$int e^{2 x+1} sin x d x+frac{1}{4} int e^{2 x+1} sin x d x=-e^{2 x+1} cos x+frac{e^{2 x+1} sin }{2}$
или
$frac{5}{4} int e^{2 x+1} sin x d x=-e^{2 x+1} cos x+frac{e^{2 x+1} sin x}{2}$
Далее домножая левую и правую части равенства на $frac{4}{5}$ , окончательно имеем:
$int e^{2 x+1} sin x d x=-frac{4 e^{2 x+1} cos x}{5}+frac{2 e^{2 x+1} sin x}{5}+C$
Ответ. $int e^{2 x+1} sin x d x=-frac{4 e^{2 x+1} cos x}{5}+frac{2 e^{2 x+1} sin x}{5}+C$
Читать дальше: простейшие дроби.

































