Треугольник
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак  . Так, запись
. Так, запись  ABC будет читаться: треугольник ABC .
ABC будет читаться: треугольник ABC .
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота  ABC. Отрезок EL высота
ABC. Отрезок EL высота  DEF, опущенная на продолжение стороны DF.
DEF, опущенная на продолжение стороны DF.
Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса  ABC.
ABC.
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана  ABC.
ABC.
Вершина треугольника


Средняя оценка: 4.2
Всего получено оценок: 192.
Средняя оценка: 4.2
Всего получено оценок: 192.
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.
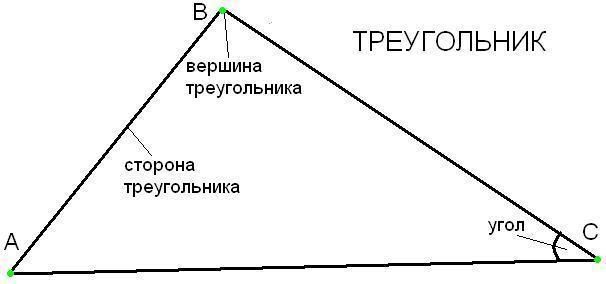 Рис. 1. Вершина в треугольнике.
Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.

Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Вершина треугольника – определение
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.

Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.

Рис. 2. Обозначение вершин в треугольнике.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.

Рис. 3. Свойство внешнего угла треугольника.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
[spoiler title=”источники:”]
http://obrazovaka.ru/matematika/vershina-treugolnika.html
http://sprint-olympic.ru/uroki/matematika-uroki/15500-vershina-treygolnika-opredelenie.html
[/spoiler]
Вершина треугольника


4.2
Средняя оценка: 4.2
Всего получено оценок: 215.
4.2
Средняя оценка: 4.2
Всего получено оценок: 215.
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

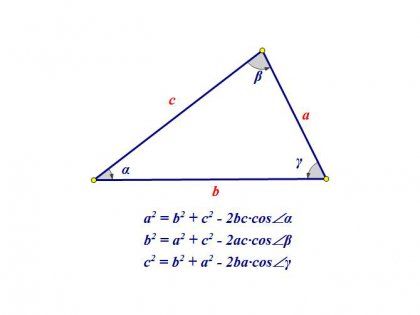
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.
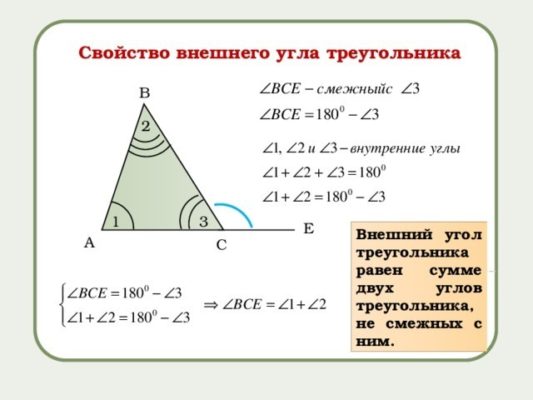
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.

Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Лёня Кондратьев
5/5
-

Али Юсупов
3/5
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 215.
А какая ваша оценка?
Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)

- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
![]()
получим систему уравнений
![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)
Вычтем из первого уравнения системы второе:
![]()
![]()
![]()
![]()
Теперь из второго уравнения системы вычтем третье:
![]()
![]()
![]()
Приравняем правые части равенств b=-2a+10 и b=3a-20:
![]()
![]()
![]()
![]()
Подставим в первое уравнение системы a=6 и b=-2:
![]()
![]()
![]()
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
![]()
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости

Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой: 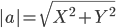
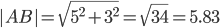
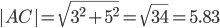
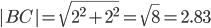
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле: 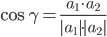
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC 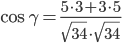
γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2) , представляется уравнениями: 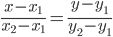
Уравнение прямой AB . Каноническое уравнение прямой: 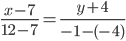 или
или 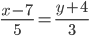
y= 3 /5x- 41 /5 или 5y-3x+41=0
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.

Содержание
- Определение вершины треугольника
- Характеристики понятия
- Использование вершины треугольника
- Что мы узнали?
Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.

Рис. 2. Обозначение вершин в треугольнике.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.

Рис. 3. Свойство внешнего угла треугольника.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Предыдущая
МатематикаЧто такое отрезок в математике? (тема математики, 5 класс)
Следующая
МатематикаВиды треугольников – острый, равнобедренный, равносторонний (5 класс, математика)
Раз уж вы нашли косинус и синус угла в треугольнике – дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.
Но есть и решение в векторах, вообще без тригонометрии.
Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны – AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:

Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:
(rC-rA)² = a²
(rC-rB)² = b²
Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:
(rC-rA)² - (rC-rB)² = a² - b²
(rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b²
2rC(rB-rA) + rA² - rB² = a² - b²
2rC(rB-rA) = a² - b² - (rA² - rB²)
У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм. Этой прямой по построению принадлежат точки C и C’ – значит, это уравнение прямой CC’. Кстати, разности rB – rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).
В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием “сингулярность”: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная – деление на ноль будет при попытке выразить x через y.
Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’. Напомню, что параметрический вид уравнения прямой выглядит вот так:
r = r0 + t u
Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем – задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.
Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:
r = rA + tAB
2r·AB = a² - b² - (rA² - rB²)
Подставим первое уравнение во второе и решим его относительно переменной t:
2(rA + tAB)·AB = a² - b² - (rA² - rB²)
2rA·AB + 2t AB² = a² - b² - (rA² - rB²)
t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB²
t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB²
t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB²
t = (a² - b² + (rA - rB)²) / 2AB²
t = (a² - b² + AB²) / 2AB²
Осталось подставить эту переменную обратно в параметрическое уравнение:
t = (a² - b² + AB²) / 2AB²
r0 = rA + tAB
Формула выглядит страшно, но не имеет сингулярностей пока A и B – разные точки. Даже в случае некорректных начальных данных у тут будет какое-то решение.
Кстати, для проверки корректности формулы можно подставить сюда вырожденные треугольники: при a=0, b=AB точка r0 окажется равна rA; а при a=AB, b=0 точка r0 окажется равна rB. Пока всё нормально.
И так, у нас есть точка r0, осталось найти направляющий вектор прямой CC’. Ну, это тоже просто: надо лишь взять вектор AB и повернуть его на прямой угол в любую сторону. Это делается тоже просто, если вектор AB был с координатами (xB – xA, yB – yA) – то повёрнутый будет с координатами (-yB + yA, xB – xA). Почему так – объясняется по ссылке, которую я уже приводил ранее. Обозначим его через AB^.
Ну, теперь у нас есть параметрическое уравнение прямой CC’ и уравнение одной из окружностей, осталось их пересечь и мы найдём точки C и C’.
rC = r0 + k AB^
(rC-rA)² = a²
И снова мы можем просто подставить одно уравнение в другое (вот почему я так люблю параметрические уравнения прямых в задачах на геометрию!):
(r0-rA + k AB^)² = a²
k² AB^² + 2k AB^ (r0-rA) + (r0-rA)² - a² = 0
Тут есть и дальнейшие упрощения: вектор r0–rA сонаправлен AB, а потому при умножении на AB^ будет чистый ноль, можно и не считать. Кстати, длина вектора AB^ равна длине вектора AB, что тоже позволяет чуть упростить формулу.
Суммируя всё что написано выше, получаем следующую систему уравнений:
t = (a² - b² + AB²) / 2AB²
k² AB² = a² - t² AB²
r0 = rA + t AB
rC = r0 + k AB^
Осталось решить примитивное квадратное уравнение:
t = (a² - b² + AB²) / 2AB²
k = ± sqrt(a² / AB² - t²)
rC = rA + t AB + k AB^
Дальше осталось перейти от векторов к координатам и решение готово.
