Как найти максимальную скорость

Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.
Запишите уравнение зависимости скорости от времени.
Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.
Из полученных значений t выберите точки максимума функции. Точка максимума — это минус.
Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.
Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.
Движение тела, брошенного под углом к горизонту

H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .
h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .
l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .
H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .
H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )
H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )
H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )
H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )
H = 1 , 4 + 0 , 6 = 2 ( м )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17980 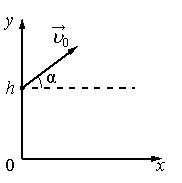
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.



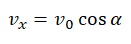

pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Как найти предельную скорость
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 11 человек(а).
Количество просмотров этой статьи: 34 610.
Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.
Как найти максимальную скорость
Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.

Инструкция
Запишите уравнение зависимости скорости от времени.
Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.
Из полученных значений t выберите точки максимума функции. Точка максимума – это минус.
Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.
Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.
Видео по теме
Полезный совет
Функцию зависимости скорости от времени можно получить, дифференцируя функцию пройденного пути, либо интегрируя функцию ускорения. Во втором случае понадобятся еще начальные условия.
Источники:
- как находится максимальная скорость
Как найти предельную скорость
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 11 человек(а).
Количество просмотров этой статьи: 34 506.
Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.
Как определить максимальную и минимальную скорости движущихся объектов — манекены — Бизнес — 2022
Одним из наиболее практических применений дифференциации является поиск максимальных или минимальных значений функции реального мира, например максимальной и минимальной скоростей движущегося объекта.
Вы можете представить v elocity как более техническую версию скорость .
Вот пример. Йо-йо движется прямо вверх и вниз. Его высота над землей, как функция времени, задается функцией H ( t ) = t 3 — 6 t 2 + 5 t + 30, где t находится в секундах и H ( t ) находится в дюймов. При t = 0 yo-yo составляет 30 дюймов над землей, а через 4 секунды он находится на высоте 18 дюймов, как показано на этом рисунке.

Высота yo-yo, от 0 до 4 секунд.
Чтобы определить общее расстояние, пройденное yo-yo, вам нужно добавить расстояния, пройденные на каждой ноге поездки yo-yo: вверх нога, нога и вторая нога.
Во-первых, йо-йо поднимается с высоты от 30 дюймов до 31 дюймов (где первая точка поворота). Это расстояние около 1,1 дюйма. Затем он опускается примерно с 31. 1 до 16. 9 (высота второй точки поворота). Это расстояние 31. 1 минус 16. 9, или около 14. 2 дюйма. Наконец, yo-yo снова поднимается с 16 дюймов до конечной высоты 18 дюймов. Это еще 1 дюйм. Добавьте эти три расстояния, чтобы получить общее пройденное расстояние:

Примечание: Сравните этот ответ с общим объемом перемещения — 12, который вы получаете от вычитания конечной высоты yo-yo, 18 дюймов, от ее начальная высота 30 дюймов. Смещение отрицательно, потому что движение сети вниз. И положительная величина смещения (а именно 12) меньше расстояния, пройденного 16. 4, потому что при смещении верхние ноги рейса yo-yo отменяют часть расстояния вниз. Посмотрите математику:

Средняя скорость yo-yo определяется общим пройденным пройденным расстоянием, деленным на прошедшее время. Таким образом,

Скажем, вы определяете, что максимальная скорость yo-yo составляет 5 дюймов в секунду, а ее минимальная скорость составляет -7 дюймов в секунду. Скорость -7 — это скорость 7, так что это максимальная скорость yo-yo. Его минимальная скорость равна нулю в двух оборотных точках.
Хорошим способом анализа максимальной и минимальной скорости является рассмотрение функции скорости и ее графика. (Или, если вы являетесь обжором для наказания, ознакомьтесь со следующим mumbo jumbo.) Скорость равна абсолютному значению скорости.
Velocity, V ( t ), является производной от позиции (высота, в этой задаче). Таким образом:

Итак, для задачи yo-yo, функция скорости,

Посмотрите на график S ( t ) на следующем рисунке.

Функция скорости yo-yo S ( t )
Глядя на этот график , легко видеть, что максимальная скорость yo-yo происходит при t = 2

и что минимальная скорость равна нулю на двух x -перехватах.
Минимальная и максимальная скорость: Для непрерывной функции скорость минимальная скорость равна нулю всякий раз, когда максимальная и минимальная скорости имеют противоположные знаки или когда один из них нуль. Когда максимальная и минимальная скорости являются как положительными, так и отрицательными, скорость минимум меньше абсолютных значений максимальной и минимальной скоростей. Во всех случаях максимальная скорость представляет собой больше абсолютных значений максимальной и минимальной скоростей. Это глоток или что?
Как найти максимальную скорость по графику
Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.
Берем любую точку, например, 0.
— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)
Берем например, точку 1.
— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)
Значит, t = 1/2 — это точка максимума.
Подставим это значение в уравнение скорости.
v = — 30t 2 + 30t + 2
v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.
Ответ: максимальная скорость движения равна 9,5.
Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

- Попроси больше объяснений
- Следить
- Отметить нарушение
Ответ

Ответ:
Объяснение:
Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)
1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²
S = 0 + 15*1/2 = 7,5 м
2. S = V*t = 15*3 = 45 м
3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.
Еще раз о том, что такое равноускоренное движение
Автомобиль за каждую секунду увеличивает свою скорость на  . Движется ли автомобиль равноускоренно?
. Движется ли автомобиль равноускоренно?
На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением  . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).
. Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).
Уравнение скорости
Воспользовавшись уравнением, определяющим ускорение  , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:
, удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:


Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.
К вопросу о направлении скорости и ускорения
В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения.
1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой
В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.
2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой
Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.
3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны
Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.
Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.
График скорости
График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения
Проанализируем различные графики.
Первый. Уравнение проекции скорости: 


Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:



График начинается в точке 
Где 

Рис. 5. График функции 
Это уравнение прямой, что подтверждается графиками, рассмотренными нами.
Некоторые частные случаи
Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость,  , равняется нулю, проекция ускорения больше нуля.
, равняется нулю, проекция ускорения больше нуля.
Запись этого уравнения  . А сам вид графика достаточно простой (график 1).
. А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения
Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси .
.
Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси  . При этом модуль скорости постоянно возрастает, тело ускоряется.
. При этом модуль скорости постоянно возрастает, тело ускоряется.
График зависимости ускорения от времени
Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени
Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.
Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.


Рис. 8. Изменение скорости
Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.
Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.
Заключение
На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «youtube.com» (Источник)
- Интернет-портал «fizmat.by» (Источник)
- Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)
1. Что такое равноускоренное движение?
2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при  ?
?
Максимальную скорость
Vamax
, развивающую проектируемым автомобилем
на горизонтальной дороге, определим
как по тяговой характеристике, так и по
динамической. Допускается небольшое
несовпадение максимальных скоростей,
определенным по двум разным характеристикам;
большое несовпадение (более 4%) говорит
о погрешности в ходе проведения тягового
расчета.
Используя данные
таблицы 15, на графике тяговой характеристики
(пункт 1.7.1) строим кривую, соответствующую
суммарной силе сопротивления движения
автомобиля (сила сопротивления дороги
Fψ
плюс сила сопротивления воздуха FB);
точка пересечения данной кривой (Fψ
+ FB)
и кривой, соответствующей полной окружной
силе FK0
на высшей передаче, позволяет определить
максимальную скорость Va
max на дороге без
уклона: опустив линию на горизонтальную
ось (I = 0), по которой
отложена скорость Va
автомобиля. Если кривые Fψ
+ FB и
FK0
на высшей передаче не пересеклись, то
Vamax
соответствует максимальной скорости
по кривой FK0
на высшей передаче (данная Vamax
называется максимальной кинематической
скоростью, определяемой передаточными
числами трансмиссии и максимальной
частотой вращения коленчатого вала
двигателя); запас окружной силы FK0
в данном случае (кривые Fψ
+ FB и
FK0
не пересеклись) может быть использован
для достижения Vamax
при движении автомобиля на подъеме.
Аналогично определяется
Vamax
по динамической характеристике: используя
данные таблицы 15 на графике динамической
характеристики (пункт 1.7.2) строится для
высшей передачи кривая ψ = fV
(i=0) – безразмерного
фактора сопротивления движению
автомобиля. Точка пересечения кривой
ψ и кривой динамического фактора D
(движущего фактора) определяет Vamax,
если кривее не пересеклись, то Vamax
(кинематическая) соответствует максимуму
скорости по кривой D на
высшей передаче.
Максимально возможные
скорости движения автомобиля, определенные
по тяговой и динамической характеристикам,
должны быть равны между собой, и
соответствовать той максимальной
скорости Va
max, которая была
определена в техническом задании на
проектирование (см. пункт 1.2). Результаты
расчетов заносим в таблицу 16.
Таблица 16 – Максимальная
скорость Vаmax
автомобиля
|
Условия определения |
Vаmax |
Погрешность |
|
Тяговая характеристика |
92 |
0% |
|
Динамическая |
92 |
0% |
|
Мощносной баланс |
92 |
0% |
При движении автомобиля
на подъем (уклон дороги i)
максимальную скорость, по динамической
характеристике, в данных дорожных
условиях определяют следующим образом:
величину уклона i складывают
с коэффициентом сопротивления качению
колес fV
и ищут точку пересечения кривой i+fV
с кривой D – полученная
точка позволяет определить: какую
максимальную скорость развивает
проектируемый автомобиль и на какой
передаче в КПП.
Определяется максимальная
скорость автомобиля при преодолении
уклона в 5% и максимального уклона по
таблице 15. Найденные значения скоростей
не должны быть меньше значений, приведенных
в таблице 17.
Таблица 17 – Максимальные
скорости автомобилей
-
Максимальная скорость,
км/чГрузовые автомобили
полноприводные
неполноприводные
автопоезда
На горизонтальной
дороге, i = 080
90
80
На подъеме в 5%,
i
= 0,0540
45
25
На максимальном
подъеме i max5
12
8
Максимальная скорость
при преодолении уклона в 5%
Vаmax
= 40км/ч
Максимальная скорость
при преодолении максимального уклона
Vаmax
=7 км/ч
что соответствует
рекомендациям.
1.8
Путь и время разгона автомобиля
Считаем, что разгон
начинается с минимальной устойчивой
скорости
Vamin
(соответствующей nemin
– минимальной устойчивой частоте
вращения коленчатого вала ДВС) на
передаче, используемой для трогания
автомобиля с места. Разгон осуществляется
при полной подаче топлива т.е. двигатель
работает по ВСХ (имеем наибольшую
интенсивность разгона).
Ускорение, как известно,
можно определить по формуле:
аx![]()
(45)
где dVa
– приращение скорости за промежуток
времени dt.
Тогда
dt![]()
(46)
откуда время разгона
t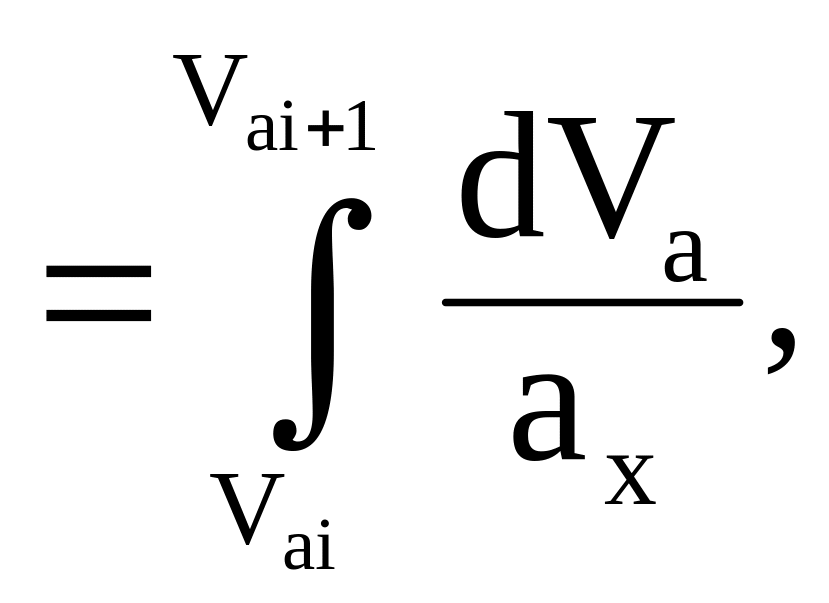
(47)
Считаем, что в небольшом
интервале скоростей ΔVai=Vai+1-Vai
движение является равноускоренным
со средним ускорением аmi
, тогда время движения в данном
интервале, между двумя точками, определим
по формуле:
![]()
(48)
где ∆Vai
– изменение скорости между двумя
точками, м/с;
Дальнейшие результаты
расчётов сведены в таблицу 18.
аmi
– среднее ускорение между двумя точками
![]()
(49)
Дальнейшие результаты
расчётов сведены в таблицу
Путь, проходимый за
время движения между двумя точками:
∆S=Vmi·∆ti
(50)
где Vmi
– средняя скорость в рассматриваемом
интервале
![]()
(51)
Дальнейшие результаты
расчётов сведены в таблицу 18.
Потери скорости за
время переключения ∆Vn
определим по формуле:
![]()
,
м/с (52)
где tn=1c
– время переключения передач
δi+1
– коэффициент учёта вращающихся масс
Путь, проходимый
автомобилем, за время переключения tn
c К-ой на К+1 передачу:
∆Sn=(Vкmax–
0,5∆Vnк-(к+1))·tn,
м (53)
где Vкmax
– скорость, соответствующая моменту
переключения
Таблица 18 – Разгон
автомобиля
Разгон автомобиля на
первой передаче
|
Пара- метр |
Раз-мер- ность |
№ точки |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
Va |
км/ч |
3,0 |
3,86 |
4,71 |
5,57 |
6,43 |
7,28 |
8,14 |
9 |
|
Va |
м/с |
0,83 |
1,07 |
1,31 |
1,55 |
1,79 |
2,02 |
2,26 |
2,5 |
|
∆Vi |
м/с |
– |
0,24 |
0,24 |
0,24 |
0,24 |
0,23 |
0,24 |
0,24 |
|
ax |
м/с2 |
0,748 |
0,816 |
0,869 |
0,899 |
0,908 |
0,899 |
0,866 |
0,818 |
|
ami |
м/с2 |
– |
0,872 |
0,843 |
0,884 |
0,904 |
0,904 |
0,883 |
0,842 |
|
∆ti |
с |
– |
0,31 |
0,29 |
0,27 |
0,27 |
0,25 |
0,27 |
0,29 |
|
t |
с |
– |
0,31 |
0,6 |
0,87 |
1,14 |
1,39 |
1,66 |
1,95 |
|
Vmi |
м/с |
– |
0,95 |
1,19 |
1,43 |
1,67 |
1,91 |
2,14 |
2,38 |
|
∆Si |
м |
– |
0,3 |
0,35 |
0,39 |
0,45 |
0,48 |
0,58 |
0,69 |
|
S |
м |
– |
0,3 |
0,65 |
1,04 |
1,49 |
1,97 |
2,55 |
3,24 |
Разгон автомобиля на
второй передаче
-
Параметр
Размерность
№ точки
9
10
11
12
13
14
Va
км/ч
8,68
9,67
11,15
12,64
14,13
15,61
Va
м/с
2,41
2,69
3,1
3,51
3,93
4,34
∆Vi
м/с
(0,09)
0,28
0,41
0,41
0,42
0,41
ax
м/с2
0,895
0,923
0,936
0,925
0,892
0,836
ami
м/с2
–
0,91
0,93
0,93
0,91
0,87
∆ti
с
(1,5)
0,31
0,44
0,44
0,46
0,47
t
с
3,45
3,76
4,2
4,64
5,1
5,57
Vmi
м/с
–
2,55
2,9
3,31
3,72
4,14
∆Si
м
3,68
0,79
1,28
1,46
1,71
1,95
S
м
6,92
7,71
8,99
10,45
12,16
14,11
Разгон автомобиля на
третьей передаче
-
Параметр
Размерность
№ точки
15
16
17
18
19
Va
км/ч
15,23
16,26
18,43
20,6
22,76
Va
м/с
4,23
4,52
5,12
5,72
6,32
∆Vi
м/с
(0,11)
0,29
0,6
0,6
0,6
ax
м/с2
0,785
0,796
0,788
0,759
0,71
ami
м/с2
–
0,791
0,792
0,77
0,735
∆ti
с
(1,5)
0,37
0,76
0,78
0,82
t
с
7,07
0,44
8,2
8,98
9,8
Vmi
м/с
–
4,38
4,82
5,42
6,02
∆Si
м
(6,43)
1,62
3,66
4,23
4,94
S
м
20,54
22,16
25,82
30,05
34,99
Разгон автомобиля на
четвёртой передаче
-
Параметр
Размерность
№ точки
20
21
22
23
24
Va
км/ч
22,31
22,42
25,41
28,4
31,39
Va
м/с
6,193
6,23
7,06
7,89
8,72
∆Vi
м/с
(0,123)
0,037
0,83
0,83
0,83
ax
м/с2
0,63
0,634
0,618
0,593
0,552
ami
м/с2
–
0,632
0,626
0,606
0,573
∆ti
с
(1,5)
0,06
1,33
1,37
1,45
t
с
11,3
11,36
12,69
14,06
15,51
Vmi
м/с
–
6,21
6,65
7,48
8,31
∆Si
м
(9,39)
0,37
8,85
10,25
12,05
S
м
44,38
44,75
53,6
63,85
75,9
Разгон автомобиля на
пятой передаче
-
Параметр
Размерность
№ точки
25
26
27
28
Va
км/ч
30,91
34,24
38,27
42,3
Va
м/с
8,586
9,51
10,63
11,75
∆Vi
м/с
(0,134)
0,924
1,12
1,12
ax
м/с2
0,465
0,47
0,443
0,408
ami
м/с2
–
0,47
0,46
0,43
∆ti
с
(1,5)
1,97
2,43
2,6
t
с
17,01
18,98
21,41
24,01
Vmi
м/с
–
9,05
10,07
11,19
∆Si
м
(12,98)
17,83
24,47
29,09
S
м
88,88
106,71
131,18
160,27
Разгон автомобиля на
шестой передаче
-
Параметр
Размерность
№ точки
29
30
31
32
Va
км/ч
41,79
45,12
50,43
55,72
Va
м/с
11,61
12,53
14,01
15,48
∆Vi
м/с
(0,142)
0,92
1,48
1,47
ax
м/с2
0,34
0,333
0,313
0,285
ami
м/с2
–
0,336
0,323
0,299
∆ti
с
(1,5)
2,74
4,58
4,92
t
с
25,51
28,25
32,83
37,75
Vmi
м/с
–
12,07
13,27
14,75
∆Si
м
(17,52)
33,07
60,78
72,57
S
м
177,79
210,86
271,64
344,21
Разгон автомобиля на
седьмой передаче
-
Параметр
Размерность
№ точки
33
34
35
36
Va
км/ч
55,18
58,17
65,01
71,86
Va
м/с
15,33
16,16
18,06
19,96
∆Vi
м/с
(0,151)
0,83
1,9
1,9
ax
м/с2
0,225
0,225
0,204
0,174
ami
м/с2
–
0,225
0,215
0,189
∆ti
с
(1,5)
3,69
8,84
10,05
t
с
39,25
42,94
51,78
61,83
Vmi
м/с
–
15,75
17,11
19,01
∆Si
м
(23,11)
58,12
151,25
191,05
S
м
367,32
425,44
576,69
767,74
Разгон автомобиля на
восьмой передаче
-
Параметр
Размерность
№ точки
37
38
39
40
Va
км/ч
71,26
74,28
83,02
92
Va
м/с
19,795
20,63
23,06
25,56
∆Vi
м/с
(0,165)
0,84
2,43
2,5
ax
м/с2
0,125
0,12
0,097
0,064
ami
м/с2
–
0,123
0,109
0,081
∆ti
с
(1,5)
6,83
22,29
30,86
t
с
63,33
70,16
92,45
123,31
Vmi
м/с
–
20,21
21,85
24,31
∆Si
м
29,82
138,03
487,04
750,21
S
м
797,56
935,59
1422,63
2172,84
По данным таблицы 18
строим графики пути и времени разгона
автомобиля, по которым определяем:
1) время разгона до
скорости 60 км/ч
t60=45с
2) путь проходимый АТС
до достижения Vamax
– Sv
Sv=2172,84м
3) время разгона с места
на пути 1000м – t1000
t1000=72c
1.9
Мощностной баланс
Расчет мощностного
баланса, проведем на высшей передаче.
Уравнение мощностного
баланса имеет вид:
NK=NB+
N+
Nia
(54)
где NК
– мощность, подведенная к ведущим
колесам:
NK
= Nе
Т, кВт
(55)
где Ne –
эффективная мощность двигателя (таб.2),
кВт;
ηТ – КПД
трансмиссии;
Nк=73,34,38·0,82=60,14
кВт
Дальнейшие результаты
расчётов сведены в таблицу 19
N
– мощность, затрачиваемая на преодоление
сопротивления дороги;
Nψ=Fψ·Va,
кВт (56)
где Fψ
– сила сопротивления дороги (таблица
15), Н;
Va –
скорость автомобиля (таблица 15),м/с;
Nψ=2900·8,5=24650Вт=24,65кВт
Дальнейшие результаты
расчётов сведены в таблицу 19
NВ
– мощность, затрачиваемая на преодоление
сопротивления воздуха:
NВ =
FB
Va,
кВт (57)
где FB
– сила сопротивления воздуха (таблица
15),Н;
NВ=51,8·5,047=261Вт=0,261кВт
Дальнейшие результаты
расчётов сведены в таблицу 12
Nia
– мощность, которая может быть затрачена
на разгон автомобиля.
Таблица 19 – Мощносной
баланс автомобиля на высшей передаче
|
ne, об/мин |
Va, км/ч |
Va, м/с |
Ne, кВт |
NК, кВт |
NВ, кВт |
NК кВт |
N, кВт |
|
700 |
30,59 |
8,5 |
73,34 |
60,14 |
1,95 |
58,19 |
24,65 |
|
900 |
39,32 |
10,92 |
102,57 |
84,11 |
4,13 |
79,98 |
32,54 |
|
1100 |
48,06 |
13,35 |
133,01 |
109,07 |
7,53 |
101,54 |
40,72 |
|
1300 |
56,8 |
15,78 |
162,73 |
133,44 |
12,43 |
121,01 |
49,71 |
|
1500 |
65,54 |
18,21 |
190,05 |
155,84 |
19,1 |
136,74 |
59,36 |
|
1700 |
74,28 |
20,63 |
212,82 |
174,51 |
27,79 |
146,72 |
69,52 |
|
1900 |
83,02 |
23,06 |
229,83 |
188,46 |
38,81 |
149,65 |
80,94 |
|
2100 |
92 |
25,56 |
239,66 |
196,52 |
52,91 |
143,61 |
94,06 |
По данным таблицы 19
строим график мощностного баланса
автомобиля на высшей передаче и определяем
Vаmax
– точка пересечения кривых Nψ
и Nк-Nв
Vаmax=92
км/ч
1.10
Топливная экономичность
Построим топливную
характеристику установившегося движения
– зависимость путевого расхода топлива
Qs от скорости
движения Vа и
определим эксплуатационный расход
топлива проектируемого автомобиля,
(все расчёты будем вести на высшей
передаче).
Путевой расход будет
определяться по зависимости:
![]()
,
л/100 км (58)
где geN
– средний удельный эффективный расход
топлива при максимальной мощности
двигателя, г/кВтч;
geN
= (1,05 … 1,1) gemin
(59)
где gemin
– минимальный удельный расход топлива,
г/кВтч;
gemin
= 180 … 240 г/кВтч;
geN
=1,05·180=189 г/кВтч
KИ
– коэффициент использования мощности
двигателя;
KИ =
1, 2 + 0,14 · U – 1.8 · U2
+ 1,46 · U3
(60)
![]()
(61)
![]()
Дальнейшие результаты
расчётов сведены в таблицу 20
KИ =
1,2 + 0,14 · 0,442 – 1,8 · 0,442 2 + 1,46 · 0,442 3=
1,036
Дальнейшие результаты
расчётов сведены в таблицу 20
KЕ
– коэффициент использования частоты
вращения коленчатого вала двигателя;
KЕ
= 1,25 – 0,99 · Е + 0,98 · Е2 – 0,24 · Е3
(62)
![]()
(63)
где ne,
Va –
текущая соответственно частота вращения
коленчатого вала и скорость АТС;
nN,
VaN –
соответственно частота вращения
коленчатого вала и скорость автомобиля
при максимальной мощности двигателя;
![]()
Дальнейшие результаты
расчётов сведены в таблицу 20
KЕ
= 1,25 – 0,99·0,333 + 0,98·0,3332 –
0,24·0,3333=1,018
Дальнейшие результаты
расчётов сведены в таблицу 20
N
и NВ – см. таблицу
19
T
– плотность топлива, кг/м3 : для
дизельного топлива;
T=835
кг/м3
Va,
км/ч – см. таблицу 15
![]()
л/100 км
Дальнейшие результаты
расчётов заносим в таблицу 20 и строим
топливную характеристику автомобиля,
по которой определяем:
1) расход топлива при
скорости 80км/ч и 60км/ч
расход топлива при
скорости 80км/ч равен 35,5 л/100 км
расход топлива при
скорости 60км/ч равен 30,2 л/100 км
2) эксплуатационный
расход (э.р.) топлива
э.р. = 1,1·QP
(64)
где QP
– путевой расход при расчетной скорости
VP
![]()
;
(65)
![]()
км/ч;
QP=32,4
л/100 км;
э.р. = 1,1·32,4=35,64 л/100 км;
3) контрольный расход
топлива Qк –
минимальный расход по топливной
характеристике
Qк=28
л/100 км
Таблица 20 – Топливная
экономичность автомобиля на высшей
передаче
-
Va,
км/чNК,
кВтN
+ NВ,кВт
U
E
KИ
KЕ
QS
,л/100кмч
30,59
60,14
26,6
0,442
0,333
1,036
1,018
25,32
39,32
84,11
36,67
0,436
0,427
1,04
0,987
26,43
48,06
109,07
48,25
0,442
0,522
1,036
0,966
27,74
56,8
133,44
62,14
0,466
0,617
1,022
0,956
29,5
65,54
155,84
78,46
0,504
0,712
1,001
0,955
31,59
74,28
174,51
97,31
0,558
0,807
0,972
0,963
33,85
83,02
188,46
119,75
0,635
0,902
0,937
0,978
36,48
92
196,52
146,97
0,748
1
0,909
1
40,08
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лучший ответ
daybit
Высший разум
(146360)
10 лет назад
400 м делишь на 32 секунды, получаешь среднюю скорость 12.5 м/с, или 45 км/ч. никаких максимальных или минимальных скоростей. только средняя
Остальные ответы
Сергей Гаврилов
Искусственный Интеллект
(184997)
10 лет назад
Никак. Среднюю скорость легко найти.
Михаил Иванов
Профи
(822)
10 лет назад
максимальная скорость может быть указана в документах, прилагаемых к велосипеду когда он продается, а из указанных данных можно найти лишь скорость с которой велик проехал в данном случае, и она равна 400 м / 32 с = 12.5 м/с
Александр Николаев.
Просветленный
(35193)
10 лет назад
Это можно найти если к тому же знать как зависело ускорение от времени.
Если к примеру велосипед двигался всё время равно ускоренно то S=a*t*t/2
S=Vmax*t/2; Vmax=S*2/t=400*2/32=25метров в секуду
