У этого термина существуют и другие значения, см. Масса (значения).
Не следует путать с весом.
| Масса | |
|---|---|
 |
|
| Размерность | M |
| Единицы измерения | |
| СИ | кг |
| СГС | г |
Ма́сса — скалярная физическая величина, определяющая инерционные и гравитационные свойства тел в ситуациях, когда их скорость намного меньше скорости света[1]. В обыденной жизни и в физике XIX века масса синонимична весу[2].
Будучи тесно связанной с такими понятиями механики, как «энергия» и «импульс», масса проявляется в природе двумя качественно разными способами, что даёт основания для подразделения её на две разновидности:
- инертная масса характеризует инертность тел и фигурирует в выражении второго закона Ньютона: если заданная сила в инерциальной системе отсчёта одинаково ускоряет различные тела, им приписывают одинаковую инертную массу;
- гравитационная масса (пассивная и активная) показывает, с какой силой тело взаимодействует с внешними полями тяготения[3] и какое гравитационное поле создаёт само это тело[4], она входит в закон всемирного тяготения и положена в основу измерения массы взвешиванием.
Однако экспериментально с высокой точностью установлена пропорциональность гравитационной и инертной масс[5][6], и подбором единиц они сделаны в теории равными друг другу. Поэтому, когда речь не идёт об особой «новой физике», принято оперировать термином «масса» и использовать обозначение m без пояснений.
Массой обладают все макроскопические объекты, бытовые предметы, а также большинство элементарных частиц (электроны, нейтроны и др.), хотя среди последних имеются и безмассовые (например, фотоны). Наличие массы у частиц объясняется их взаимодействием с полем Хиггса.
Масса в классической механике[править | править код]
Простое определение инертной массы[править | править код]
Величина массы входит в нерелятивистское выражение второго закона Ньютона F = ma, дающее связь между силой и вызываемым ею ускорением свободного тела. Указанный закон, одновременно с утверждением линейности соотношения «сила—ускорение», по сути, выступает определением инертной массы. Сила при этом определяется логически независимо и от закона Ньютона, и от понятия «ускорение»[7]: она равна деформации специальной тестовой пружины (с точностью до калибровочного множителя).
Масса может измеряться в килограммах. Официальным эталоном массы «1 кг» по 2018 год служил конкретный объект (см. фото выше); по соглашению, если приложенная к эталону сила обеспечивает ускорение 1 м/с2, то такая сила имеет величину 1 Н. Данным соглашением задаётся единичная сила — приложив её к упомянутой пружине, можно прокалибровать последнюю и использовать для измерений. Инертная масса любого исследуемого тела находится затем как F / a: достаточно знать ускорение при каком-то одном значении силы.
В 2018 году учёные заменили эталон килограмма, хранящийся в Международном бюро мер и весов во Франции с 1889 года. Теперь единица массы определяется с помощью постоянной Планка. Для создания нового эталона массы применяются весы Киббла — устройство, которое определяет, какой ток нужен для того, чтобы создать электромагнитное поле, способное уравновесить чашу с тестируемым эталоном[8]. Старый эталон отныне играет роль очень точной гири.
Гравитационная масса. Принцип эквивалентности[править | править код]
По своему смыслу гравитационная масса — характеристика тел в классической механике, являющаяся мерой их гравитационного взаимодействия
где G — гравитационная постоянная (константа Ньютона), r — расстояние между материальными точками, обладающими гравитационными массами 

Первая проверка пропорциональности двух видов массы была выполнена Галилеем, изучавшим свободное падение. Согласно опытам Галилея, все тела, независимо от их массы и материала, падают с одинаковым ускорением. Сейчас эти опыты можно трактовать так, что увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Позднее на пропорциональность инертной и гравитационной масс обратил внимание Ньютон, он же впервые доказал, что эта пропорциональность выдерживается с точностью не хуже 0,1 %[9].
С учётом сказанного раздельных единиц для гравитационной и инертной массы не вводят, а коэффициент их пропорциональности принят равным 1 с надлежащим подбором константы G. На сегодня пропорциональность (условно говоря, «равенство масс») экспериментально проверена с очень высокой точностью: чувствительность к относительной разности в лучшем эксперименте на 2009 год[5][6] имеет порядок 10−13.
Подобные эксперименты привели к формулированию принципа эквивалентности:
Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.
имеющего два уровня глобальности охвата «всех явлений». Так называемый «сильный» принцип гласит: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в неускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы. «Слабый» принцип отличается заменой слов «законы природы» словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.
Единицы измерения массы[править | править код]
Килограмм является одной из семи основных единиц СИ. По современному определению, его величина выражается через величины трёх выбранных физических постоянных: постоянная Планка, скорость света и частота определённого электронного перехода.
В Международной системе единиц (СИ) масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (1⁄1000 килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их числа произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс·с²/м (называлась «техническая единица массы» или «инерта»). В атомной физике и химии принято сравнивать [соотносить] массу с относительной атомной массой (а.е.м.), в физике твёрдого тела — с массой электрона (Атомная система единиц), в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрофизике единицей для сравнения масс небесных тел служит масса Солнца.
В некоторых естественных системах единиц в качестве единицы массы используются массы элементарных частиц: электрона или протона[10]. В планковской системе единиц, также относящейся к естественным системам, единицей массы является планковская масса.
Массы очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны: 1 см-1 ≈ 3,52⋅10-41 кг. Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом: 1 см ≈ 6,73⋅1024 кг.
Основные свойства массы как величины[править | править код]
Масса — одна из важнейших величин в физике. Это скалярная неотрицательная релятивистски инвариантная величина. По современным представлениям, масса эквивалентна энергии покоя (mc2, где c — скорость света в вакууме). Масса входит в выражения кинетической энергии (mv2/2, где v — скорость) и импульса (mv) материальной точки.
Масса тела, выраженная в килограммах, численно примерно равна весу этого тела, выраженному в кгс (1 кгс ≈ 10 Н), когда оно покоится вблизи поверхности Земли. Поэтому в повседневных ситуациях слово «вес» нередко синонимизируется со словом «масса». Однако это разные понятия, и в общем случае численные значения массы и веса не совпадают, не говоря уже о различии размерностей. Например, при помещении предмета на обычные магазинные весы показания колеблются в течение нескольких секунд: в это время вес претерпевает изменения, а масса постоянна. Также возможны ситуации с нулевым весом и ненулевой массой одного и того же тела: в условиях невесомости вес всех тел равен нулю, а масса у каждого тела своя.
В классической механике масса инвариантна относительно смены системы отсчёта и аддитивна, то есть масса системы тел равна сумме масс составляющих её тел.
Масса в релятивистской механике[править | править код]
Строгое определение массы[править | править код]
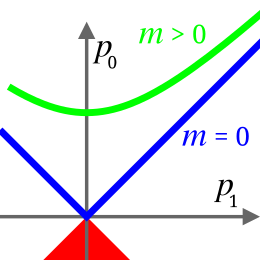
Возможные 4-импульсы тел с нулевой и положительной массой покоя. Векторы 4-импульса, построенные от точки пересечения осей до любой точки на зелёной гиперболе, имеют одну и ту же (положительную) длину, то есть массу частицы, несущей этот четырёхимпульс, и различаются энергией и 4-скоростью частицы. Ускорение частицы сводится к движению конца 4-импульса по гиперболе. Векторы четырёхимпульса, построенные от точки пересечения осей до любой точки на синих полупрямых, имеют нулевую длину и могут относиться только к частицам нулевой массы (например, фотонам); энергия этих частиц (с точностью до коэффициента
c) равна модулю их 3-импульса
Наиболее строгое определение массы даётся в специальной теории относительности (СТО): масса — это абсолютная величина 4-вектора энергии-импульса[11]:
где E — полная энергия свободного тела, p — его 3-импульс, c — скорость света. В СТО масса является неаддитивной, но, как и в классической физике, инвариантной величиной.
В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:
Здесь 

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то 
Особенно просто выглядят эти определения в системе единиц, в которой за единицу измерения скорости принята скорость света (например, в планковской или же в принятой в физике элементарных частиц для описания процессов при высоких энергиях релятивистской системе единиц, в которой масса, импульс и энергия имеют размерность энергии[12] и измеряются в электронвольтах):
- В СТО:
- В ОТО:
Частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300 000 км/с), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.
О «массе покоя» и «релятивистской массе»[править | править код]
В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом подразделе.
В большом количестве источников[13][14], относящихся к началу и середине XX века, а также в научно-популярных[15], введённое выше понятие массы называли «массой покоя», при этом саму массу вводили на основе классического определения импульса
В таком случае 
Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство
где m — инвариантная масса, а uμ — 4-скорость (производная от 4-координаты по собственному времени частицы 
Также можно записать ковариантный эквивалент второго закона Ньютона:
где 
Масса составных и нестабильных систем[править | править код]
В релятивистской механике, в отличие от классической, масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс её компонентов. Масса системы зависит от характера движения частиц друг относительно друга и в случае взаимодействующих частиц также включает в себя энергию связи[Комм 1].
Масса устойчивой системы взаимодействующих частиц, совершающих финитное движение (например, нуклонов в атомном ядре), может зависеть от внутреннего состояния этой системы. Она меньше суммы масс частиц на величину 


Масса системы невзаимодействующих релятивистских частиц не меньше суммы их масс и равна данной сумме, только когда все частицы покоятся друг относительно друга[18]. Это утверждение следует из того, что в релятивистской механике массой системы частиц называется модуль её четырёхимпульса[19]: 





Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: 
Классификация частиц по значению массы[править | править код]
- Масса частиц микромира
Масса всех известных на сей день частиц является неотрицательной величиной. В физике элементарных частиц понятие массы чрезвычайно важно, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света, как фотоны) от массивных (скорость которых всегда ниже скорости света).
Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения, меняющего частицы и античастицы). Наличие массы у кварков и лептонов объясняется их взаимодействием с полем Хиггса, и чем сильнее это взаимодействие, тем больше масса[20][21]. Масса элементарной частицы постоянна, она одинакова у всех частиц данного типа и их античастиц. В то же время в физике элементарных частиц рассматриваются объекты без определённой массы (которые также можно называть элементарными частицами); эти частицы являются линейными квантовомеханическими комбинациями частиц, имеющих определённую массу (массовых состояний). Так, нейтрино с определёнными флейворами (то есть электронное, мюонное и тау-нейтрино и соответствующие им антинейтрино) не имеют определённых масс, и наоборот, массовые состояния нейтрино не обладают определёнными флейворами, а являются смесью флейворных состояний; этот факт является причиной нейтринных осцилляций. То же относится и к ряду нейтральных мезонов (K0, B0– и D0-мезоны). В частности, K0
и K0
-мезоны, являющиеся собственными состояниями гамильтониана сильного взаимодействия, не обладают, строго говоря, определённой массой (и временем жизни), будучи суперпозицией двух массовых состояний K0
S и K0
L (см. Смешивание нейтральных каонов); однако разность масс m(K0
S) − m(K0
L) = 3,5·10−6 эВ настолько мала по сравнению с их массой mK ≈ m(K0
S) ≈ m(K0
L) ≈ 497,611 МэВ и даже с экспериментальной погрешностью её измерения (13 кэВ), что можно считать массу каона K0
и антикаона K0
определённой и равной mK[22].
- Положительная масса
К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны (включая нейтрино, которые в первоначальной версии Стандартной модели считались безмассовыми), кварки, W- и Z-бозоны, бозон Хиггса. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: барионы (в том числе протон и нейтрон) и мезоны.
- Нулевая масса
К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому говорят о «скорости света»). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.
Комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.
- Отрицательная масса
Частицы с отрицательной массой двигались бы с любой скоростью, меньшей скорости света, аналогично тардионам, и имели бы отрицательную энергию и импульс, направленный в сторону, противоположную направлению движения. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. В то же время в общей теории относительности допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. В частности, подобную область можно создать с помощью эффекта Казимира[23].
- Мнимая масса
В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.
Измерение массы[править | править код]
Методы и устройства для измерения[править | править код]
Основная статья: Весы
Большинство приборов для измерения массы основано на использовании принципа эквивалентности инертной и гравитационной массы. С помощью таких приборов, называемых весами, массу тел определяют по их весу. В пружинных весах вес измеряется по степени деформации гибкой пружины. В рычажных — вес определяется путём сравнения веса интересующего тела с весом эталонов (гирь) известной массы.
Однако в ситуации невесомости (скажем, на космических станциях) весы неприменимы, и используются другие устройства — массметры, действие которых основано на измерении периода свободных колебаний груза на пружине; этот период, как известно, зависит от массы тела.
Массы заряженных элементарных частиц определяют по их следам в камере Вильсона[24]. Массы короткоживущих элементарных частиц, не оставляющих следов в камере Вильсона, определяют, оценивая суммарную энергию продуктов их распада[25][26].
Массу Земли определяют на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной и радиуса Земли[27]. Массу Солнца определяют также на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной, расстояния между Землёй и Солнцем и периода обращения Земли вокруг Солнца[28]. Масса нашей Галактики определяется исходя из периода обращения окрестностей Солнца вокруг центра Галактики и расстояния до центра Галактики[29].
Массы ближайших двойных звезд определяются по расстоянию между ними и периоду их обращения. Если звезда не имеет спутника и принадлежит главной последовательности, то её массу можно определить исходя из её светимости или температуры поверхности[30].
Значения масс различных объектов[править | править код]
| Объект | Масса (кг) | В других единицах | |
|---|---|---|---|
| Нейтрино | < 1,5⋅10−37 | < 0,12 | эВ |
| Электрон | 9,1⋅10−31 | 5,1⋅105 | эВ |
| Протон | 1,7⋅10−27 | 9,4⋅108 | эВ |
| Бозон Хиггса | 2,4⋅10−25 | 1,3⋅1011 | эВ |
| Вирус гриппа | 6⋅10−19 | 4⋅108 | а.е.м. |
| Снежинка | 1⋅10−7 | 0,1 | мг |
| Человек | 80 | 176 |
фунт |
| Слон | 4,5⋅103 | 4,5 | тонн |
| Кит | 1,5⋅105 | 150 | тонн |
| Пирамида Хеопса | 6,0⋅109 | 6,0⋅106 | тонн |
| Земля | 6,0⋅1024 |  |
масс Земли |
| Юпитер | 1,9⋅1027 |  |
масс Земли |
| Солнце | 2,0⋅1030 |  |
масс Солнца |
| Другие звёзды | 4,0⋅1028—1,8⋅1032 | 0,02—90 | масс Солнца |
| Наша Галактика | 2,6⋅1041 | 1,3⋅1011 | масс Солнца |
| Другие галактики | 2,0⋅1036—2,0⋅1043 | 106—1013 | масс Солнца |
Этимология и история понятия[править | править код]
Слово масса (лат. massa, от др.-греч. μαζα) первоначально в античные времена обозначало кусок теста. Позднее смысл слова расширился, и оно стало обозначать цельный, необработанный кусок произвольного вещества; в этом смысле слово используется, например, у Овидия и Плиния[31]. В ряде областей науки и техники это слово (часто во множественном числе) до сих пор продолжает использоваться в значении какой-либо относительно однородной субстанции (воздушные массы, пластмасса, бумажная масса, селевая масса, народные массы).
Масса как научный термин для меры количества вещества была введена Ньютоном, до этого естествоиспытатели оперировали понятием веса. В труде «Математические начала натуральной философии» (1687) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон ввёл массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе[32]. Ньютон явно указал на эту пропорциональность и даже проверил её на опыте со всей возможной в те годы точностью: «Определяется масса по весу тела, ибо она пропорциональна весу, что мной найдено опытами над маятниками, произведенными точнейшим образом»[33] (эти опыты Ньютон подробно описал в III томе своих «Начал»).
Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения[34]. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, оно сохранялось в XVII—XIX веке, но затем подверглось критике как нефизическое и бессодержательное[35]. В настоящее время понятие «количество вещества» применяется, но имеет совершенно другой смысл.
Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии и во многих ситуациях не соблюдается.
Обобщения понятия массы[править | править код]
Прямые обобщения понятия массы включают в себя такие тензорные характеристики, как момент инерции, и такие показатели свойств системы «тело плюс среда», как массовое водоизмещение, присоединённая масса и эффективная масса, используемые в гидростатике, гидродинамике и квантовой теории.
Например, введение так называемой эффективной массы позволяет учесть взаимодействие электрона (или дырки) с периодическим электромагнитным полем кристаллической решетки в полупроводнике, что необходимо для корректного квантовомеханического описания движения носителей заряда.
См. также[править | править код]
- Эквивалентность массы и энергии
- Принцип эквивалентности сил гравитации и инерции
- Скрытая масса
- Сравнение массы и веса
- Эффективная масса
Комментарии[править | править код]
- ↑ Так, например, суммарная масса двух свободных частиц зависит от угла между их импульсами. В частности, масса системы, состоящей из двух фотонов, обладающих энергией Е каждый, равна нулю, если импульсы фотонов сонаправлены, и равна 2E/c2, если их импульсы направлены в противоположные стороны[15].
Примечания[править | править код]
- ↑ Окунь Л. Б. Масса // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 50—52. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Дмитрий Иванович Сахаров, Михаил Иванович Блюдов. Физика для техникумов «Наука», 1969. С. 28.
- ↑ Неравенство пассивной гравитационной и инертной масс протяженного тела. Дата обращения: 23 июля 2014. Архивировано 13 августа 2014 года.
- ↑ Вебер Дж. — Общая теория относительности и гравитационные волны. Дата обращения: 25 июля 2014. Архивировано 27 июля 2014 года.
- ↑ 1 2 Phys. Rev. Lett. 100, 041101 (2008): Test of the Equivalence Principle Using a Rotating Torsion Balance
- ↑ 1 2 [1]Архивная копия от 21 октября 2016 на Wayback Machine [0712.0607] Test of the Equivalence Principle Using a Rotating Torsion Balance
- ↑ Матвеев А. Н. Механика и теория относительности. — М.: ОНИКС, 2003. — 432 с. — ISBN 5-329-00742-9 [гл. 5, §§ 19—20].
- ↑ Мировой эталон килограмма заменили. lenta.ru. Дата обращения: 13 декабря 2018. Архивировано 18 ноября 2018 года.
- ↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5. Дата обращения: 18 февраля 2011. Архивировано 4 января 2010 года.
- ↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7., § 9. Энергия и импульс.
- ↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 6.
- ↑ Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с.
- ↑ Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с.
- ↑ 1 2 3 Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?» // Успехи физических наук. — 2000. — Т. 170, № 12. — С. 1366—1371. — doi:10.3367/UFNr.0170.200012j.1366.
- ↑
Окунь Л. Б. Понятие массы (Масса, энергия, относительность) (Методические заметки) // УФН. — 1989. — Т. 158. — С. 511—530. - ↑ Широков Ю. М. Ядерная физика. — М., Наука,1980. — С. 37.
- ↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 25.
- ↑ В этом абзаце для простоты используется рассмотренная выше система единиц с = 1.
- ↑ Рубаков В. А. Долгожданное открытие: бозон Хиггса Архивная копия от 29 октября 2013 на Wayback Machine // Наука и жизнь. — 2012. — № 10. — С. 20—40. — ISSN 0028-1263. —
- ↑ Садовский М. В. Лекции по квантовой теории поля. — Москва-Ижевск : Институт компьютерных исследований, 2003. — С. 370 — ISBN 5-93972-241-5. — URL: http://eqworld.ipmnet.ru/ru/library/books/Sadovskij2002ru.pdf Архивная копия от 9 сентября 2016 на Wayback Machine
- ↑ Герштейн С. С., Захаров В. И. K-мезоны // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 384—388. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition Архивировано 17 июля 2012 года., Physical Review, 61, 13, September 1988, pp. 1446—1449
- ↑ Завельский, 1970, с. 119.
- ↑ Завельский, 1970, с. 123.
- ↑ Копылов Г. И. Всего лишь кинематика. — М.: Атомиздат, 1968. — 176 с.
- ↑ Завельский, 1970, с. 136.
- ↑ Завельский, 1970, с. 150.
- ↑ Завельский, 1970, с. 161.
- ↑ Киппенхан Р. 100 миллиардов солнц. Рождение, жизнь и смерть звезд. — М.: Мир, 1990. — С. 281—284 — ISBN 5-03-001195-1.
- ↑ Джеммер, М., 1967, Глава I.
- ↑ Спасский Б. И. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
- ↑ Ньютон И. Математические начала натуральной философии, том I, определение 1.
- ↑ Тюлина И. А. Об основах ньютоновой механики (к трёхсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: Изд-во Моск. ун-та, 1989. — Вып. 36. — С. 184—196..
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: НИЦ РХД, 2000. — 456 с. — ISBN 5-89806-023-5.
Литература[править | править код]
- Джеммер, Макс. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
- Переиздание: Едиториал УРСС, 2003, ISBN 5-354-00363-6.
- Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
- Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
- L. B. Okun. On the concepts of vacuum and mass and the search for higgs (англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — doi:10.1142/S0217732312300418. — arXiv:1212.1031.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
- Gordon Kane. The Mysteries of Mass. // Scientific American. June 27, 2005.
- Завельский Ф. С. Взвешивание миров, атомов и элементарных частиц. — М.: Атомиздат, 1970. — 176 с.
Статьи[править | править код]
- Государственный первичный эталон единицы массы ГЭТ 3-2008
Содержание:
- Масса
- Второй закон Ньютона
- Масса — мера инертности тела
- Система единиц измерения механических величин
- Примеры решения задач на второй закон Ньютона
Масса – это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Масса
Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.
Массой тела называется количество вещества, содержащегося в этом теле.
Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.
Рис. 98. Измерение массы тела.
Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.
За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.
В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).
В практике эталоны масс изготовляют в виде гирь различной величины.
Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.
Второй закон Ньютона
Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.
Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.
Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле 
Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.
Результаты таких измерений и вычислений отражены в таблице.
Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.
Математически это можно записать в виде формулы:
Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.
Нагружая тележку гирями, изменим массу движущихся тел.
Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.
Результаты опытов снова занесём в таблицу.
Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:
Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.
Кроме того, ускорение тела совпадает с этой силой по направлению.
Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.
Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.
Второй закон Ньютона математически можно выразить в виде следующей формулы:

Величина силы равна произведению массы тела на ускорение.
Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.
В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:
Р = mg.
Из сопоставления формулы F=ma и P=mg видно, что
т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.
При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.
Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением 
Р=70 кГ;
g=
а =
F = ?
Из формулы 
Масса — мера инертности тела
Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.
Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.
Рис. 100. Масса наковальни значительно больше массы молота.
Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона 
Итак, масса тела является мерой его инертности.
Из второго закона Ньютона 
Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.
Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.
Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.
Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.
Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.
Рис. 101. Машина на массивном фундаменте.
Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.
Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:
Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.
Система единиц измерения механических величин
Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.
Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в
Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.
Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.
В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( 
Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).
Единица скорости в этой системе 
Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:
За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным 
В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:
единица длины — 1 м,
единица массы — 1 кг,
единица времени — 1 сек,
единица тока — 1 ампер.
Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).
Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением 
Вычислим, сколько в одном ньютоне содержится дин.

В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:
единица длины —1 м,
единица силы —1 кГ,
единица времени—1 сек.
Единица массы в этой системе единиц является производной и может быть определена из равенства 
Сокращённое обозначение этой единицы—т. е. м. Таким образом,
Между различными единицами массы и силы существуют следующие соотношения:
1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение 

Так как 
Примеры решения задач на второй закон Ньютона
1. Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?
Расчёты ведём в системе CGS.
Дано: F = 2 кГ=2*980000 дн = 1960000 дн;
m=19600 г; t = 5 сек. Найти
Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:
Время t дано по условиям задачи.
Ускорение найдем на основании второго закона:
Ответ:
2. Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.
Дано: Р = 98 кГ; 
Искомую силу найдём на основании второго закона:
F = mа.
Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;



По второму закону Ньютона Р = mg, откуда
Ответ.
3. На тело, движущееся с начальной скоростью в 
Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона:
Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, 
откуда
Масса тела
Ответ.
При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.
Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.
Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.
Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.
m = 10 г; t = 60 сек.; s = 1800 см.
По второму закону Ньютона F = ma. (1)
Масса дана, ускорение а находим по формуле пути равноускоренного движения: 
Подставим значение а из равенства (2) в равенство (1), получим:
Подставляя численные значения величин в равенство (3), определим величину силы F:
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Масса является одним из важных свойств материи. Это понятие применяют при решении задач различного характера, начиная от проблем в механике и заканчивая химическими расчетами. Рассмотрим в статье, с помощью каких формул массу в физике можно рассчитать.
Что это такое?
Прежде чем приводить формулы массы в физике, дадим ей определение. Этим термином называется физическая величина, которая пропорциональна количеству материи, заключенной в данном теле. Следует не путать ее с количеством вещества, которое выражается в молях. Масса в СИ вычисляется в килограммах. Другими ее единицами являются тонны и граммы.

Масса бывает двух важных видов:
- инерционная;
- гравитационная.
Первый вид рассматриваемой физической величины характеризует инерционные свойства тела, то есть способность некоторой силы изменять скорость тела, а также кинетическую энергию, которой оно обладает.
Гравитационная масса связана с интенсивностью притяжения между любыми телами. Она играет важную роль в космосе, поскольку благодаря притяжению между звездами и планетами существует наша галактика и наша Солнечная система. Однако гравитационная масса проявляет себя и в повседневной жизни в виде наличия у всех тел некоторого веса.
Формулы для инерции
В физике формула нахождения массы инерционной имеет следующий вид:
m = F / a
Здесь F – сила, которая на тело действует и вызывает появление у него ускорения a. Формула показывает, что чем больше будет действующая сила и чем меньше она сообщит ускорение телу, тем больше инерционная масса m.
Помимо записанного выражения, следует привести еще одну формулу нахождения массы в физике, которая связана с явлением инерции. Эта формула имеет вид:
m = p / v
Здесь p – количество движения (импульс), v – скорость тела. Чем большим количеством движения обладает тело и чем меньше его скорость, тем большую инерционную массу оно имеет.
Формула для гравитации
Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:
F = G * m1 * m2 / r2
Где r – расстояние между телами, G – некоторая постоянная.
Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:
m = F / g
Здесь F – сила тяжести, g – ускорение, с которым тела падают на землю вблизи ее поверхности.
Как известно, наличие силы тяжести обуславливает то, что все тела имеют вес. Многие путают вес и массу, полагая, что это одна и та же величина. Обе величины действительно связаны через коэффициент g, однако вес – величина изменчивая (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса в килограммах.
Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.

Плотность и объем
Как было отмечено, масса – это неотъемлемое свойство материи, поэтому ее можно вычислить с помощью других физических характеристик тел. Этими характеристиками являются объем и плотность.
Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.
Плотность – это свойство вещества, которое отражает количество материи, помещенной в единице объема.
Формула массы вещества через объем и плотность записывается так:
m = ρ * V
Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.
Относительная
Понятие об относительной массе применяется в атомной физике и в химии. Поскольку массы атомов и молекул имеют очень маленькие значения (≈10-27 кг), то оперировать ими на практике при решении задач оказывается крайне неудобно. Поэтому сообществом ученых было решено использовать так называемую относительную массу, то есть рассматриваемая величина выражается в единицах массы по отношению к массе известного эталона. Этим эталоном стала 1/12 массы атома углерода, которая равна 1,66057*10-27 кг. Соответствующая относительная величина получила название атомной единицы (а. е. м.).

Формулу относительной массы M можно записать так:
M = ma / (1 / 12 * mC)
Где ma – масса атома в килограммах, mC – масса атома углерода в килограммах. Например, если в это выражение подставить значение массы атома кислорода, то его а. е. м. будет равна:
M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.
Поскольку а. е. м. является относительной величиной, то она не имеет размерности.
Удобство применения этого термина на практике заключается не только в небольших и целых значениях этой единицы измерения. Дело в том, что значение а. е. м. совпадает по величине с молярной массой, выраженной в граммах. Последняя представляет собой массу одного моль вещества.
Энергия

Выше были приведены разные формулы, как найти массу в физике. Завершая статью, хотелось бы отметить связь массы и энергии. Это связь носит фундаментальный характер, который отражает пространственно-временные свойства нашей Вселенной. Соответствующая формула массы в физике, полученная Альбертом Эйнштейном, имеет вид:
E = m * c2
Квадрат скорости света c является коэффициентом перевода между массой и энергией. Это выражение говорит о том, что обе величины, по сути, являются одной и той же характеристикой материи.
Записанное выражение было подтверждено экспериментально при изучении ядерных реакций и реакций элементарных частиц.
Содержание:
- Определение и формула массы тела
- Инертная масса
- Гравитационная масса
- Формула расчета массы через плотность тела
- Масса в специальной теории относительности
- Примеры решения задач
Определение и формула массы тела
Определение
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна
сумме масс всех отдельных частей системы (mi):
$$m=sum_{i=1}^{n} m_{i}(1)$$
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$bar{F}=m bar{a}(2)$$
где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать
величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой
тяжести (Ft) избранного тела:
$$m=frac{F_{t}}{g}(3)$$
где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.
Формула расчета массы через плотность тела
Масса тела может быть рассчитана как:
$$m=int_{V} rho d V(4)$$
где $rho$ – плотность вещества тела, где интегрирование
проводится по объему тела. Если тело однородное ( $rho = const$ ),
то масса может быть рассчитана как:
$m = rho V (5)$
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
$$m=sqrt{frac{E^{2}}{c^{4}}-frac{p^{2}}{c^{2}}}$$
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
$$m=frac{m_{0}}{sqrt{1-frac{v^{2}}{c^{2}}}}(7)$$
где m0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
В СГС: [m]=гр.
Примеры решения задач
Пример
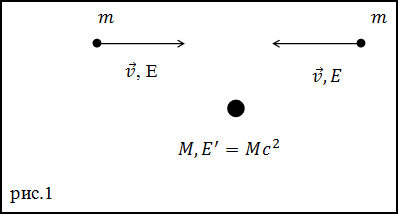
Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.
Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:
$$E^{prime}=M c^{2}(1.1)$$
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:
$$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$
где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.
Закон сохранения энергии запишем в виде:
$$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$
Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:
$$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=rho V$$
При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 cdot 2=17800$ (кг)
Ответ. $m=8900 cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Download Article
Download Article
Mass is one of the fundamental properties of an object in Physics, and is a measurement of how much matter there is in something. Matter is any substance that you can touch — anything that takes up physical space and has volume. Often, mass is related to size, but this isn’t a perfect relationship, as objects like a large hot-air balloon often have less mass than a small boulder. To calculate mass, you’ll first need the density and volume of the object. Read on for details of the formula and to learn about different types of mass across scientific disciplines.
-
1
Look up the object’s density. Density measures how tightly the matter in an object is packed together. Each material has its own density, which you can look up online or in a textbook. The scientific unit of density is kilograms per cubic meter (kg/m3), but you can use grams per cubic centimeter (g/cm3) for smaller objects.
- Use this formula to convert between these units: 1,000 kg/m3 = 1 g/cm3
- The density of liquids is often measured in kilograms per liter (kg/L) or grams per milliliter (g/mL) instead. These units are equivalent: 1 kg/L = 1 g/mL.
- Example: Diamond has a density of 3.52 g/cm3.
-
2
Measure the object’s volume. The volume is the amount of space the object occupies. Measure the volume of solids in cubic meters (m3) or cubic centimeters (cm3), and the volume of liquids in liters (L) or milliliters (mL). The formula for volume depends on the shape of the object. Refer to this article for common shapes.
- Use the same unit that appears as part of your density measurement.
- Example: Since we measured the density of diamond in g/cm3, we should measure our diamond’s volume in cm3. Let’s say our diamond’s volume is 5,000 cm3.
Advertisement
-
3
Multiply the volume and density together. Multiply your two numbers together, and you’ll know the mass of your object.[1]
Keep track of the units as you do this, and you’ll see that you end up with units of mass (kilograms or grams).- Example: We have a diamond with volume 5,000 cm3 and density 3.52 g/cm3. To find the diamond’s mass, multiply 5,000 cm3 x 3.52 g/cm3 = 17,600 grams.
Advertisement
-
1
Determine mass with force and acceleration. Newton’s second law of motion states that force equals mass times acceleration: F = ma. If you know the net force on the object, and it’s acceleration, you can rearrange this formula to find the mass: m = F / a.
- Force is measured in N (newton), which you can also write as (kg * m)/ s2. Acceleration is measured in m/s2. When you calculate F / a, the units cancel to give you an answer in kilograms (kg).[2]
- Force is measured in N (newton), which you can also write as (kg * m)/ s2. Acceleration is measured in m/s2. When you calculate F / a, the units cancel to give you an answer in kilograms (kg).[2]
-
2
Understand mass and weight. Mass is the amount of matter in an object; this does not change unless you cut off part of the object, or attach more material. Weight is a measurement of gravity’s effect on mass. If you move the object to an area with different gravity (such as from the earth to the moon), it’s weight will change, but it’s mass will not. [3]
- An object with more mass does weigh more than an object with less mass, if they’re experiencing the same gravity.
-
3
Calculate molar mass. If you’re doing your chemistry homework, you may come across the term “molar mass.” This is a related concept, but instead of measuring an object, you measure exactly one mole of a substance. Here’s how to calculate it in most contexts:
- For an element: look up the atomic mass of the element or compound you are measuring. This will be in “atomic mass units” (amu). Multiply by the molar mass constant, 1 g/mol, to put it into standard molar mass units: g/mol.
- For a compound: add the atomic masses of each atom in the compound to find the total amu of the molecule. Multiply this total by 1 g/mol.
Advertisement
-
1
Use a triple-beam balance. The balance is a device widely used to calculate an object’s mass. The balance has three beams. These beams carry weights. [4]
The weights allow you to move known masses along the beams.[5]
- The triple beam balance is not affected by gravity. Thus, it gives a true measurement of mass. It works by comparing a known mass to an unknown mass.
- The middle beam reads in 100g increments. The far beam reads in 10g increments. The weights will sit in a notch. The weight on the front beam can read from 0 to 10 grams.
- You should be able to get a very precise measurement of mass with this balance. The reading error for a triple-beam balance is only 0.06 grams. Think of the triple-beam balance as operating like a teeter-totter.[6]
-
2
Move the three sliders to their leftmost positions. You want to do this maneuver when the pan is empty. You want the balance to read zero.
- If the indicator on the far right does not align with the fixed mark, you should calibrate the balance by turning the set screw that you will find on the left under the pan.
- The reason you need to do this is because you need to make sure that the empty pan is 0.000g so its weight does not skew the mass reading you ultimately get. The weight of the container or pan is called its tare.
- You can also set the pan to 0 by screwing the knob under the pan in or out. Again, the balance must read zero. Place the object to be measured on the pan. You are now ready to determine the object’s mass using the sliding beams.
-
3
Move the sliding beams one at a time. First, move the 100-gram slider along the beam to the right first. Do this until the indicator drops below the fixed mark. The position that is to the left of this point indicates the number of hundreds of grams. You are sliding it one notch at a time.
- Move the 10-gram slider along the beam to the right. Do this until the indicator drops below the fixed mark. The notched position immediately to the left of this point indicates the number of tens of grams.
- The beam in the front does not have notches. You can move the slider anywhere you want on the beam. The beam’s boldface numbers are grams. The tick marks between the boldface numbers indicate tenths of grams.
-
4
Calculate the mass. You are now ready to find the mass of the object you placed in the pan. To do so, you should add the numbers from the three beams.
- Read the front scale as you would a ruler. You can read it to the nearest half tick mark.
- For example, let’s say you are trying to measure a can of soda. If the rear weight is in the notch that reads 70g, if the middle weight is in the notch reading 300g, and if the the front beam weight is 3.34g, then the can of soda weighs 373.34g.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you calculate the mass of a solution?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
To find the total mass of a solution, you’ll need to add the mass of the solute to the mass of the solvent. If you don’t know the mass of the solvent or the solute, you can calculate them if you know their density and volume.
-
Question
How do you calculate mass from weight?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Divide the object’s weight by the acceleration of gravity to find the mass. You’ll need to convert the weight units to Newtons. For example, 1 kg = 9.807 N. If you’re measuring the mass of an object on Earth, divide the weight in Newtons by the acceleration of gravity on Earth (9.8 meters/second2) to get mass.
-
Question
How do you calculate mass from weight?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Divide the object’s weight by the acceleration of gravity to find the mass. You’ll need to convert the weight units to Newtons. For example, 1 kg = 9.807 N. If you’re measuring the mass of an object on Earth, divide the weight in Newtons by the acceleration of gravity on Earth (9.8 meters/second2) to get mass.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
You can use online calculators to find the mass if you know the volume and density.[7]
[8]
-
The symbol for mass is m or M.
Advertisement
-
Don’t use pounds and ounces to measure mass; these are units of weight, and not used in scientific contexts. Technically, in the United States, the measurement of mass is called a “slug.”[9]
Advertisement
Video
References
About This Article
Article SummaryX
To calculate the mass of an object, look up the recorded density of the object online or in a textbook, which will be in units of kg/m3 or g/cm3. Then, multiply the density of the object by it’s measured volume. Make sure that your measurements for volume and density are in the same units! For example, if you have a diamond with a volume of 5,000 cm3 and density of 3.52 g/cm3, multiply 5,000 cm3 by 3.52 g/cm3 to get the mass of 17,600 grams. If you want to learn how to find mass using a balance scale, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,094,440 times.
Reader Success Stories
-
Michelle John
Nov 17, 2020
“It really helped me. Cause I’m in JSS2 and we didn’t do physics, chemistry and biology so I am new to it.…” more