Как можно найти наименьшее значение выражения

Общая информация

Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.

Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:

1. Нахождение области определения функции (ОДФ).
2. Понятие дифференциала и основные методы его нахождения.
3. Умение решать уравнения.
4. Знание графиков простых функций.
5. Основные типы функций, полуинтервал и интервал.

Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.

Наибольшее и наименьшее значение функции на отрезке

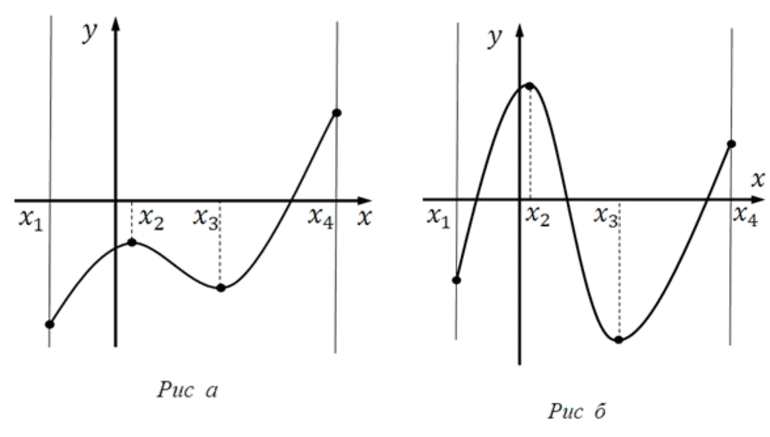
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [—6;6].

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [—3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.

Видео

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям.  Их определяет вид интервала.

• Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b—f(x).
• Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+f(x).
• Если интервал имеет вид  (a;b), то нам надо вычислить односторонние пределы limx→b—f(x),limx→a+f(x).
• Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
• Если интервал выглядит как (—∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→—∞f(x).
• Если —∞; b, то считаем односторонний предел limx→b—f(x) и предел на минус бесконечности limx→—∞f(x)
• Если же —∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x),  limx→—∞f(x).

1. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4—8 в первой части материала.

Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее  и наименьшее значение в интервалах  -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в :

x2+x-6=D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62

Следовательно, производные функции существуют на всей области ее определения.

Перейдем к нахождению стационарных точек. Производная функции обращается в при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).

Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:

y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-.456limx→-∞3e1x2+x-6=3e-4=-1

Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.

Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:

limx→-3-3e1x2+x-6-4=limx→-3-3e1(x+3)(x-3)-4=3e1(-3-+3)(-3—2)-4==3e1(+)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e-4=-1

Значит, значения функции будут расположены в интервале -1; +∞

Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке  x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:

y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+3e1x2+x-6-4=limx→-3+3e1(x+3)(x-2)-4=3e1-3++3(-3+-2)-4==3e1(-)-4=3e-∞-4=3·-4=-4

У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.

Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:

y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+3e1x2+x-6-4=-4limx→2-3e1x2+x-6-4=limx→-3+3e1(x+3)(x-2)-4=3e1(2-+3)(2—2)-4==3e1—4=3e-∞-4=3·-4=-4

Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.

Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.

На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.

limx→2+3e1x2+x-6-4=limx→-3+3e1(x+3)(x-2)-4=3e1(2++3)(2+-2)-4==3e1(+)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e-4=-1

Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.

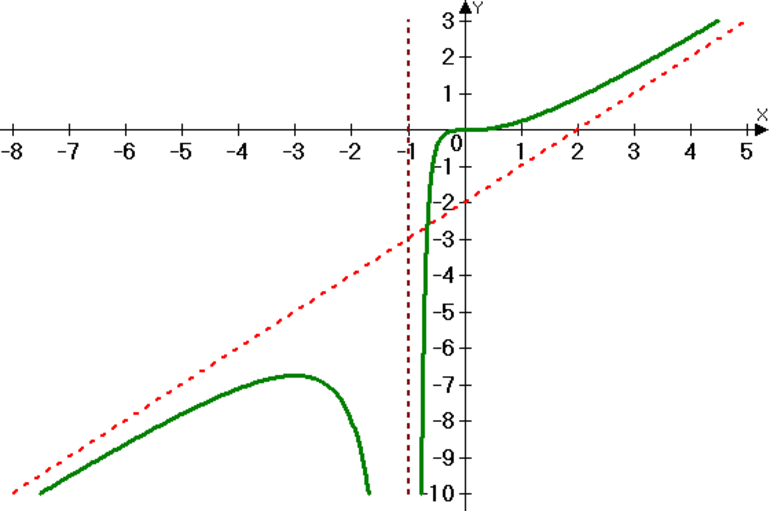
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы  хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Всё ещё сложно? Наши эксперты помогут разобраться Все услуги

Теги

Наибольшее и наименьшее значение функции

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Основные определения

Начнем, как всегда, с формулировки основных определений.

Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.

Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

Наибольшее и наименьшее значение функции на открытом интервале

Наибольшее и наименьшее значение функции на бесконечности

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.

Посмотрим, как правильно применить этот алгоритм при решении задач.

Решение:

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:

y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4

Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

Следовательно, производные функции существуют на всей области ее определения.

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Источник

Как найти наибольшее и наименьшее значение функции

Общая информация

Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.

Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:

Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.

Область определения

Область определения какой-либо функции вида y = f(x) — область значений аргумента, при которых она существует. У каждой функции существует два типа неизвестных: зависимые и независимые. К первым следует отнести переменную y, которая зависит от независимой переменной «х». Необходимо отметить, что бывают функции, в которых нет аргумента. Примером их считается функция вида y = const, где const — константа (любое число).

Обозначение интервалов

Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:

Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.

Зависимость от типа

Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:

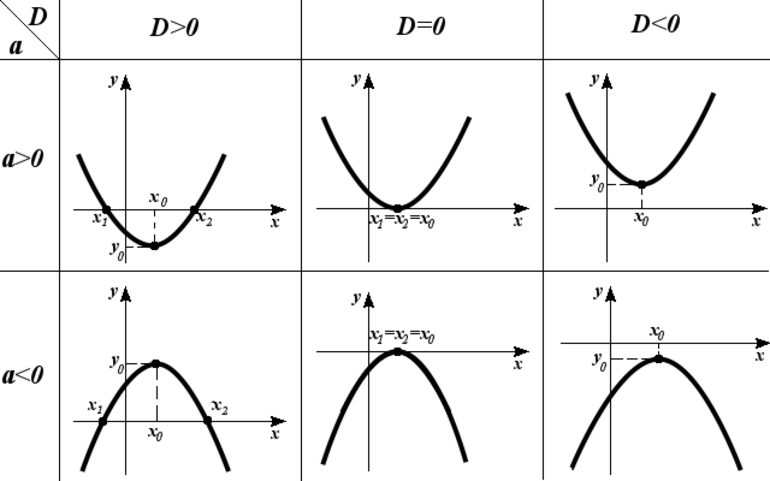
Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.

Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.

Метод нахождения

Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:

В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.

Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.

Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.

Примеры решений

Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:

Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:

Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.

Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.

Источник

Конспект урока по алгебре на тему «Наибольшее и наименьшее значение величин» (9 класс)

Ищем педагогов в команду «Инфоурок»

Тема урока: Наибольшее и наименьшее значения.

Продолжительность: 40 минут.

Цель урока: систематизировать знания по теме «Наибольшее и наименьшее значения величин».

Образовательные: способствовать формированию алгоритма нахождения наибольшего и наименьшего значений линейной и квадратичной функций.

Развивающие: способствовать развитию внимания, памяти, умственной деятельности и познавательного интереса учащихся, коммуникабельности.

Воспитательные: обеспечить условия для развития интереса к математике, уверенности в собственных силах, ответственного отношения к труду.

Тип урока: Обобщающий урок.

Оборудование: мультимедийный проектор, карточки для самостоятельной работы, презентация.

1) Организационный момент (2 минуты);

2) Актуализация опорных знаний (5 минут);

3) Мотивация (4 минуты);

4) Обобщение и решение задач по теме (13 минут);

5) Самостоятельная работа (12 минут);

6) Итог урока (2 минуты);

7) Рефлексия (2 минуты).

— формировать коммуникативную компетентность в общении и сотрудничестве с людьми в процессе образовательной деятельности;

— формировать умение соотносить полученный результат с поставленной целью.

— формировать умение устанавливать причинно-следственные связи, оценивать правильность выполнения учебной задачи, собственные возможности её решения, делать выводы;

— развитие умений использования свойств функций для нахождения наибольшего и наименьшего значений, чтения графиков функций.

1. Организационный момент

Здравствуйте, ребята! Сегодня мы с вами поговорим о задачах определённого типа, с которыми мы встречаемся очень часто в нашей жизни. Например,

1. Из проволоки длиной 10 м надо изготовить обручи, на каждый из которых идёт 45 см. Какое наибольшее количество обручей можно изготовить? (10*100/45=22,2..)

2. Из города в посёлок идёт 3 дороги. По первой, длиной 24 км, ходит автобус со скоростью 80 км/ч, по второй, длиной 20 км можно проехать со скоростью 60 км/ч, а по третьей, длиной 28 км –со скоростью 70 км/ч Какой вариант самый выгодный?

Приветствуют учителя, настраиваются на работу

Познавательные
осознанное и произвольное построение речевого высказывания.

Регулятивные
Прогнозирование своей деятельности.

Коммуникативные
Умение слушать и вступать в диалог.

Личностные
умение выделять нравственный аспект поведения.

Учитель: Великий швейцарский, немецкий и российский математик Леонард Эйлер говорил: «В мире не происходит ничего, в чём бы не был виден смысл какого-нибудь максимума или минимума». И действительно, ещё с незапамятных времён перед человеком возникают проблемы нахождения наибольшего и наименьшего, наилучшего и наихудшего.

Сформулируйте тему урока. Приведите свои примеры.

Формулируют тему урока, приводят примеры

Познавательные: самостоятельное выделение-формулирование темы, аналогия, анализ объектов с целью выделения признаков, осознанное построение речевого высказывания.

Регулятивные: определение темы урока.

3. Актуализация опорных знаний

Ученикам предлагается вспомнить, как можно найти наибольшее и наименьшее значения выражения, функции:

1. Какие вы знаете методы нахождения наименьшего и наибольшего значения выражения?

2. Как принято обозначать наименьшее и наибольшее значение функции?

3. Как найти наибольшее и наименьшее значения линейной функции на замкнутом промежутке?

4. Можно ли найти наименьшее и наибольшее значение линейной функции на незамкнутом интервале?

5. Сформулируйте алгоритм нахождения наибольшего и наименьшего значения линейной функции, заданной на отрезке.

6. Как найти наименьшее и наибольшее значение квадратичной функции на заданном множестве? Приведите возможные варианты.

7. Сформулируйте алгоритм нахождения наибольшего и наименьшего значений квадратичной функции, заданной на отрезке.

Ученики отвечают по поднятой руке, после этого ответы появляются на слайде.

Отвечают на вопросы учителя.

1. Графический, исходящий из свойств функции и пр.

5. а) Определяем монотонность (возр/убыв);

б) Подставляем концы отрезка;

в) Выбираем наименьшее и наибольшее значение;

6. Все зависит от того, входит ли абсцисса вершины в указанный отрезок. В нахождении наибольшего и наименьшего значений помогает график. (строят графики квадратичной функции, где первый коэффициент положительный и отрицательный. Выделяют интервал:

-включает абсциссу вершины,

— правее абсциссы вершины)

Познавательные
Поиск и выделение необходимой информации.

Регулятивные
Выделение и осознание того, что уже пройдено.
Постановка цели учебной задачи, темы урока.

Коммуникативные
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог.

3. Р ешение задач по теме.

№1. Найдите наименьшее и наибольшее значения линейной функции на заданном промежутке:

а) у=0,5х+3, [2; 3); б) у=2,5х-4, (1; 2];

№2. Найдите наименьшее и наибольшее значения линейной функции на заданном промежутке:

Решение: Линейная функция монотонна, значит, для того чтобы найти наибольшее и наименьшее значения, нужно вычислить значения функции на концах отрезка.

Решение: Так как функция у=2х-3 возрастает, А=2•2-3=1.

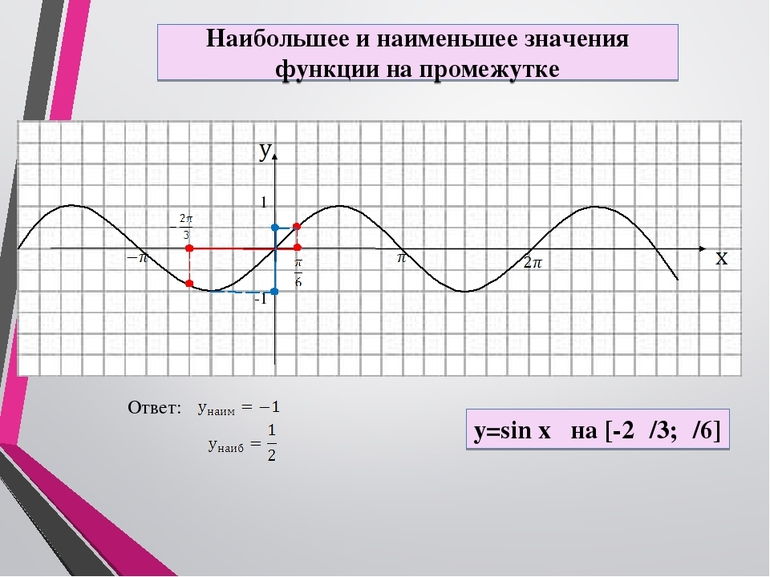
№4. График функции: у=–х 2 +2х+3. Найдите наибольшее и наименьшее значение функции

б) на полуинтервале (1;3]

Решение:

(1;4) – вершина параболы.

[0;2]: y _наим = 3 (х = 0 и х = 2); y _наиб = 4 (х = 1).

(1;3]: y _наим = 0 (х = 3); y _наиб = не существует.

№6. (Дополнительное задание, компетенция индивидуального обучения) Из квадратной заготовки жести вырезают круг. Отходы составляют 10% заготовки. Возможно ли такое?

Цель данной задачи – положить фундамент для дальнейшего изучения максимума и минимума, а также дать ученикам понять, что данная тема выходит за рамки алгебры.

Решение: Наименьшее количество отходов будет в том случае, если площадь вырезанного круга будет наибольшей, т.е. r = a /2

Значит отходы составляют не менее 21,5%.

Решают задания вместе с учителем, один ученик решает у доски, остальные в тетради, рассуждают, анализируют.

Рефлексия способов и условий действия.
Анализ и синтез объектов

Регулятивные
Планирование своей деятельности для решения поставленной задачи и контроль полученного результата

Коммуникативные
Умение слушать и вступать в диалог,

Коллективное обсуждение проблем (при необходимости).

Личностные
Ориентация в межличностных отношениях.
Развитие мышления.
Смыслообразование, развитие логического мышления.

5. Самостоятельная работа(тест)

(Компетенция индивидуального обучения)

1. Вычислите наибольшее значение линейной функции y=4x на отрезке [-2;1], не выполняя построения. (4)

2. При каком значении b принимает наименьшее значение дробь: ? ( дробь принимает наименьшее значение при b =0)

3. Найдите наименьшее и наибольшее значение функции на отрезке [0;2]. (у_наим=-2 при x=2, y_наиб=0 при х=0;)

Для тех, кто справился быстро и правильно с работой, предложить индивидуальное задание, способы решения которого имеет смысл обсудить с этой группой ребят после уроков.

Найдите наименьшее значение выражения: .

Решение: 1 способ. Для того, чтобы удобно было открывать скобки, введём новую переменную, крайний левый ноль скобок а=1, крайний правый ноль: а=6. Точка посередине: .

2 способ. Заметим, что

;

;

Пусть

Тогда , т.е. ;

;

.

Самостоятельно решают тест, работают в парах.

Коммуникативные управление поведением партнёра- контроль, коррекция, оценка.

Личностные
Ориентация в межличностных отношениях.
Развитие мышления.

Учитель: Сегодня на уроке мы рассмотрели различные виды заданий на нахождение наибольших и наименьших значений, проверили и закрепили навыки в этом вопросе, научились решать достаточно трудные задания, в конце урока провели проверочную работу, которая покажет ваш уровень подготовки по этой теме. Повторим алгоритмы, которые нам потребовались при решении задач

1. Число 10 разложите на два слагаемых так чтобы произведение этих слагаемых было наибольшим. (10 = 5+5)

2. Изобразить фигуру, ограниченную графиками функций

и . Указать координаты точки этой фигуры, имеющей наибольшую ординату. (Ответ: (3;9))

Подводят итоги вместе с учителем, анализируют свою деятельность, записывают домашнее задание.

Регулятивные: оценка-осознание уровня и качества усвоения; контроль.

Рефлексия. Выбери утверждение, которое соответствует тому, как тебе работалось на уроке.

Поднимите номер ответа на карточке и сдайте карточку мне на стол при выходе

1. Мне было всё понятно, я смог повторить теоретический материал и могу решать задачи без посторонней помощи.

2. Я вспомнил теоретический материал, решил задачи, но некоторые задачи требуют посторонней помощи.

3. Я плохо знаю теоретический материал, не смог его вспомнить и не могу решать задачи по данной теме.

Анализируют свою деятельность на уроке.

Познавательные: контроль и оценка процессов результата деятельности, адекватное понимание причин успеха и неуспеха.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник

В этой статье вы узнаете, как использовать функцию МИН в Excel 2007-2019, найти минимальное значение, наименьшее значение по условию и выделить самое маленькое число в вашем диапазоне.

Сегодня мы расскажем вам, как использовать базовую, но очень важную функцию МИН в Excel. Вы увидите способы найти минимальное значение, в том числе исключая нули, абсолютный минимум и наименьшее значение с учётом условий. Кроме того, я покажу вам пошагово, как выделить цветом наименьшее число, а также подскажу, что делать, если ваша функция МИН возвращает ошибку вместо нужного результата.

Функция МИН проверяет ваш диапазон данных и возвращает минимальное значение в этом наборе.

Синтаксис для Excel МИН следующий:

Функция МИН является одной из самых простых в применении. Вот пару примеров, доказывающих это:

1. Нахождение наименьшего значения

1: Ввести каждое значение из столбца «Количество на складе» в формулу:

2: Сделать ссылки на каждую ячейку столбца Количество:

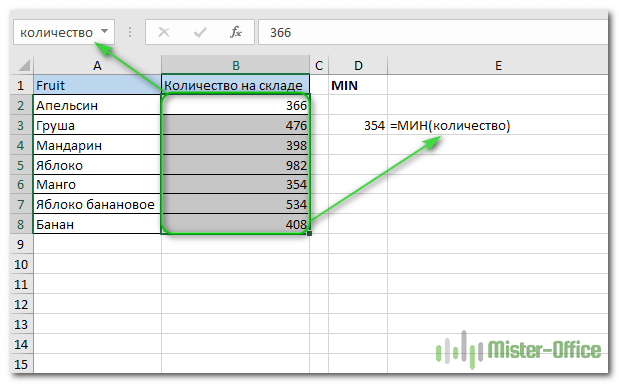
3: Или просто сослаться на весь диапазон ячеек:

4: в качестве альтернативы вы можете создать именованный диапазон и использовать его вместо этого, чтобы избежать любых прямых ссылок:

2. Как найти самую раннюю дату

Представьте, что вы ждете несколько доставок и хотели бы быть готовыми к самой ближайшей. Как узнать самую раннюю дату в Excel? Легко! Используйте функцию МИН, следуя логике из примера 1:

Примените МИН и выберите даты, ссылаясь непосредственно на ячейки:

или на именованный диапазон:

3. Поиск абсолютного минимума в Excel

Предположим, что у вас есть диапазон чисел, и вам нужно определить не просто самое маленькое из них, но найти абсолютный минимум или минимум по абсолютному значению (по модулю). Одна только МИН функция не сможет справиться с этим, поскольку она просто будет искать минимальное число. Здесь вам нужна вспомогательная функция, которая может конвертировать все отрицательные числа в положительные.

Есть ли готовое решение для этого случая? Вопрос был риторическим, в Excel есть решение любой задачи. Если у вас есть какие-либо сомнения, просто просмотрите наш блог.

Но вернемся к нашей задаче. Готовое решение для этого конкретного случая называется функцией ABS, которая возвращает абсолютное значение заданных вами чисел. Таким образом, комбинация функций МИН и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:

Как найти самое маленькое значение в Excel, исключая нули

Вам кажется, что вы уже знаете все о поиске минимальных значений в Excel? Не спешите с выводами, всегда есть чему поучиться. Например, как бы вы определили наименьшее ненулевое значение? Есть идеи? Не обманывай и не гугли, просто продолжай читать;)

Дело в том, что Excel МИН работает не только с положительными и отрицательными числами, но и с нулями. Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:

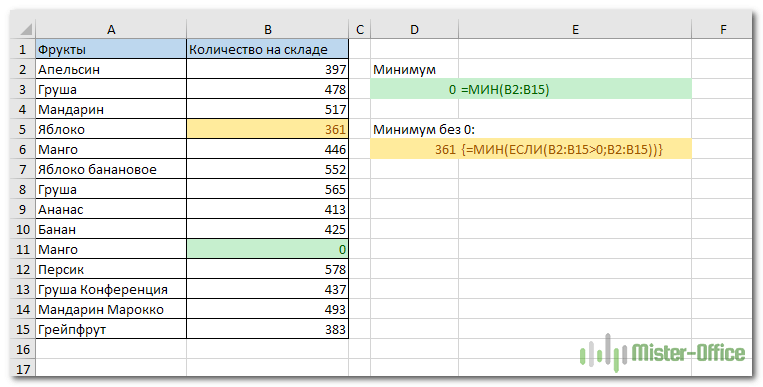
Вы, наверное, заметили фигурные скобки вокруг формулы массива. Просто помните, что вы не вводите их вручную. Они появляются в тот момент, когда вы нажимаете Ctrl + Shift + Enter на клавиатуре.

Нахождение минимума на основе условия

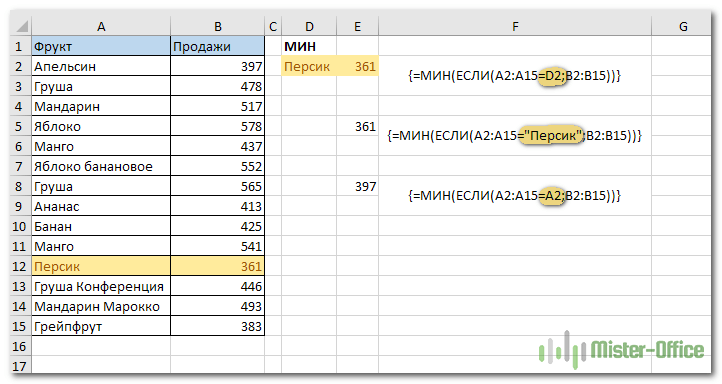
Нажмите Ctrl + Shift + Enter, чтобы эта функция массива работала, и наслаждайтесь результатом.

Выглядит довольно легко, правда? И как вы определите минимум на основе 2 или более условий? Может быть, есть более простая формула для этой задачи, доступная в Excel? Читайте дальше, чтобы узнать ответ.

Как подсветить наименьшее число в Excel

2 Когда откроется диалоговое окно «Создание правила форматирования», выберите тип правила «Форматировать только первые или последние значения».

3 Поскольку задача состоит в том, чтобы найти одно-единственное наименьшее значение, выберите опцию «последним» в раскрывающемся списке и укажите 1 в качестве количества ячеек, которые нужно выделить.

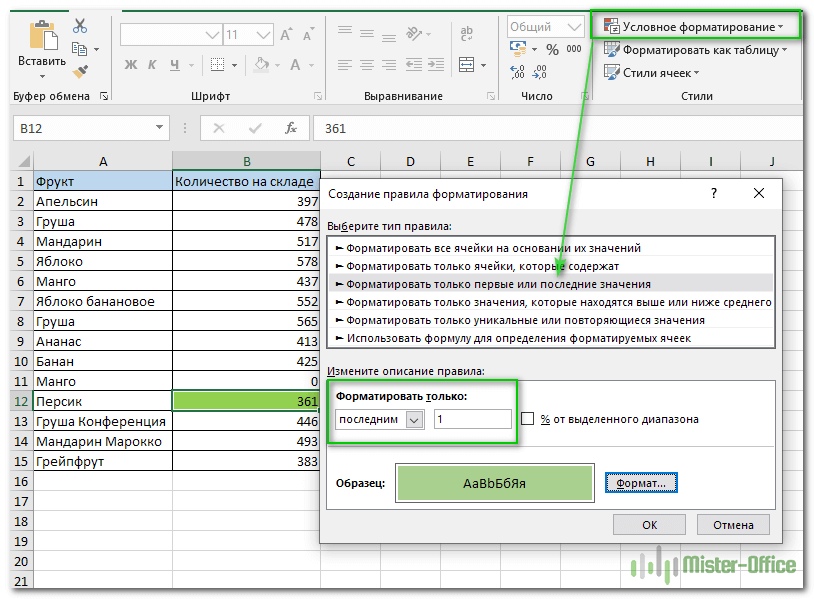
Но что делать, если в вашей таблице снова есть ноль? Как игнорировать нули при выделении минимального значения? Не беспокойтесь, для этого случая тоже есть маленькая хитрость:

1. Создайте новое правило условного форматирования, выбрав опцию «Использовать формулу для определения форматируемых ячеек».

2. Введите это выражение в поле «Значения формата» для проверки условия:

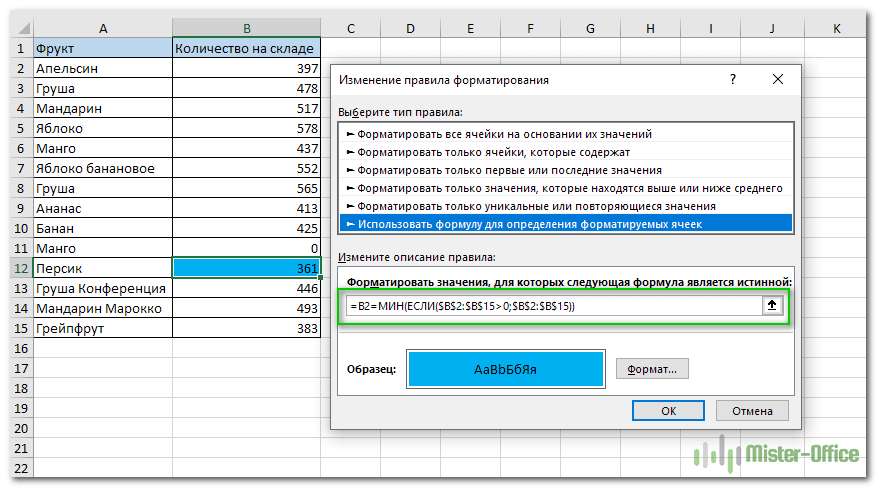
Почему не работает функция МИН?

Исправление ошибки #ЗНАЧ! в формуле МИН

Как правило, вы получаете #ЗНАЧ! сообщение об ошибке, когда хотя бы одно из значений, использованных в формуле, неверно. Что касается МИН, это может произойти, когда один из аргументов поврежден, например, что-то не так с ячейками, которые использует формула.

Например, #ЗНАЧ! может появиться, если один из аргументов является ячейкой с ошибкой или в ссылке на ячейку есть опечатка.

Я получаю сообщение #ДЕЛ/0!, что делать?

Ищете минимум, но получаете #ИМЯ?

Другая возможная причина этой проблемы лежит в именованном диапазоне. Итак, если вы ссылаетесь на несуществующий диапазон или в нем есть опечатка, вы увидите #ИМЯ? в ячейке с результатом.

Это были некоторые из способов найти минимум в Microsoft Excel с помощью функции МИН. Для вас я рассмотрел различные подходы, чтобы найти самое маленькое значение в Excel и найти абсолютный минимум. Вы можете считать эту статью своей шпаргалкой и использовать всякий раз, когда вам нужно найти минимальное число в зависимости от условия, чтобы предотвратить и исправить возможные ошибки.

Вот и все на сегодня. Пожалуйста, не стесняйтесь делиться своими мыслями и вопросами в разделе комментариев, я буду рад получить от вас обратную связь!

Источник