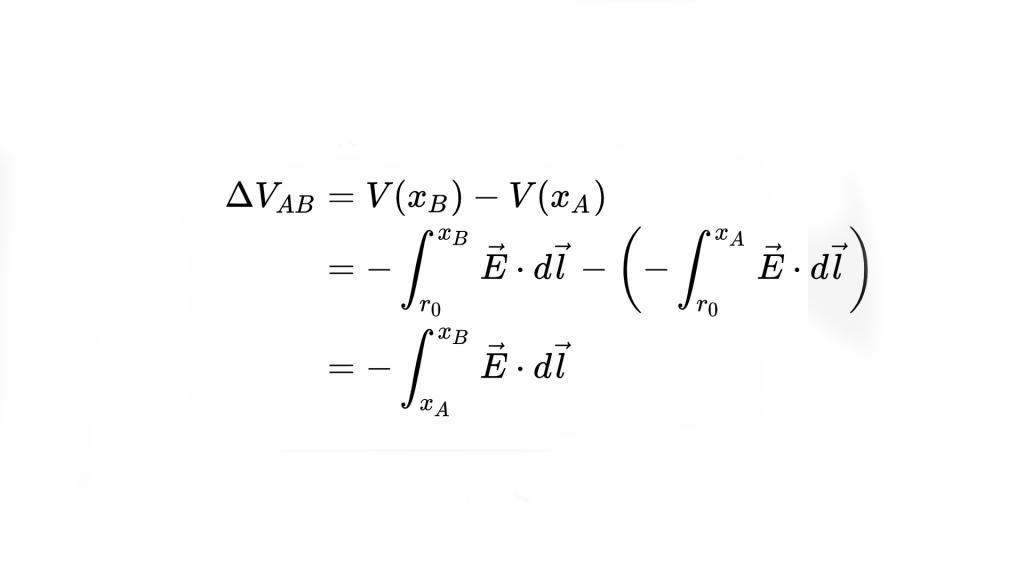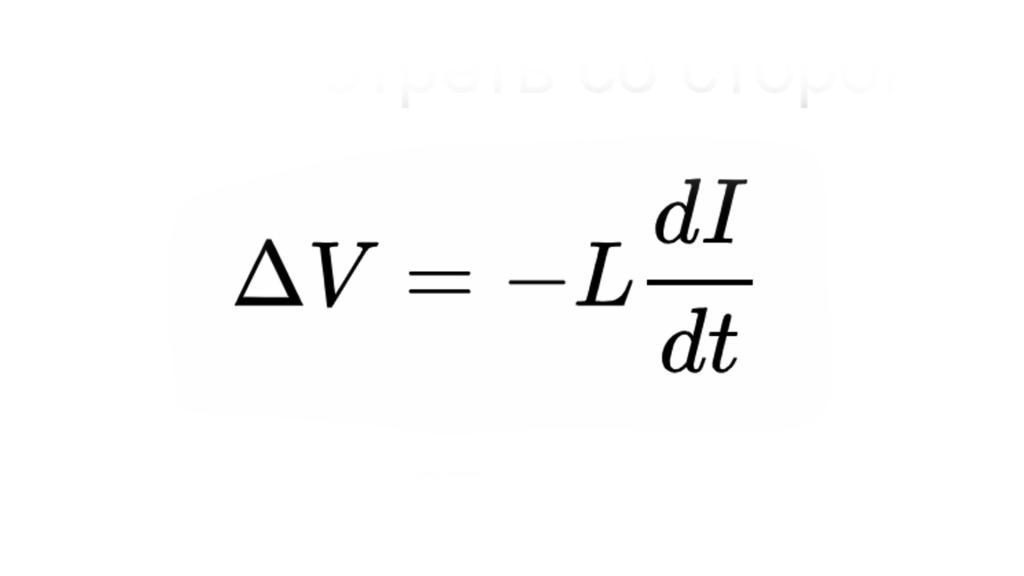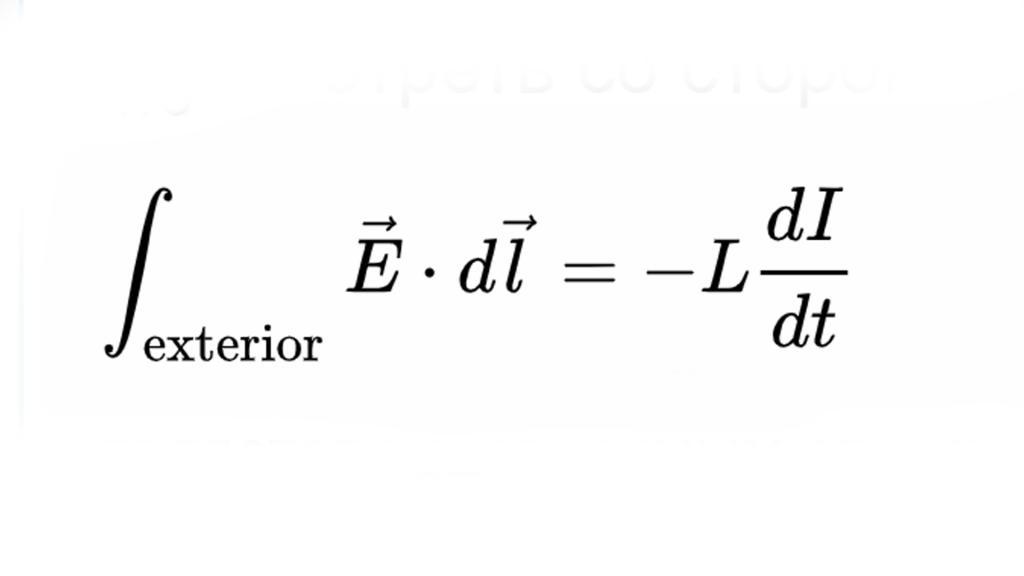Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.
Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.
Сопротивление
Формула механической мощности — средняя и мгновенная мощность
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Для переменного тока
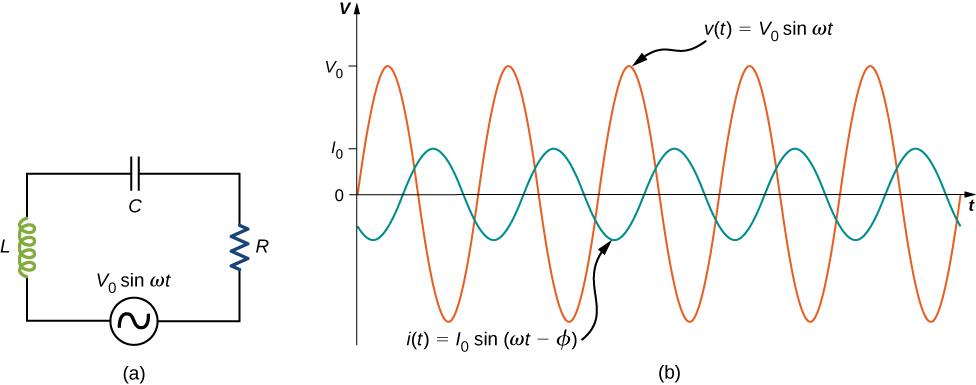
Нужно понимать, что закон не применим напрямую к переменным цепям, например, с катушками индуктивности, конденсаторами или линиям передач. Закон может использоваться только для чисто резистивных цепей переменного тока без каких-либо изменений. В цепи RLC противодействие току является импедансом Z, который образует комбинацию двух ортогональных частей сопротивления.
Переменный ток
Im=Vm/Z
В этом случае Vm связано с Im с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R. Для чисто резистивных линий, где (Z = R).
Vm = ImZ и Vm = ImR
Z — это общее сопротивление участка к переменному току, состоящее из реальной части — сопротивления и мнимой — реактивности.
Формула ее определяется теоремой Пифагора, поскольку угол Ф зависит от реактивной составляющей.
Интегральная форма
Взаимосвязь параметров электрической цепи
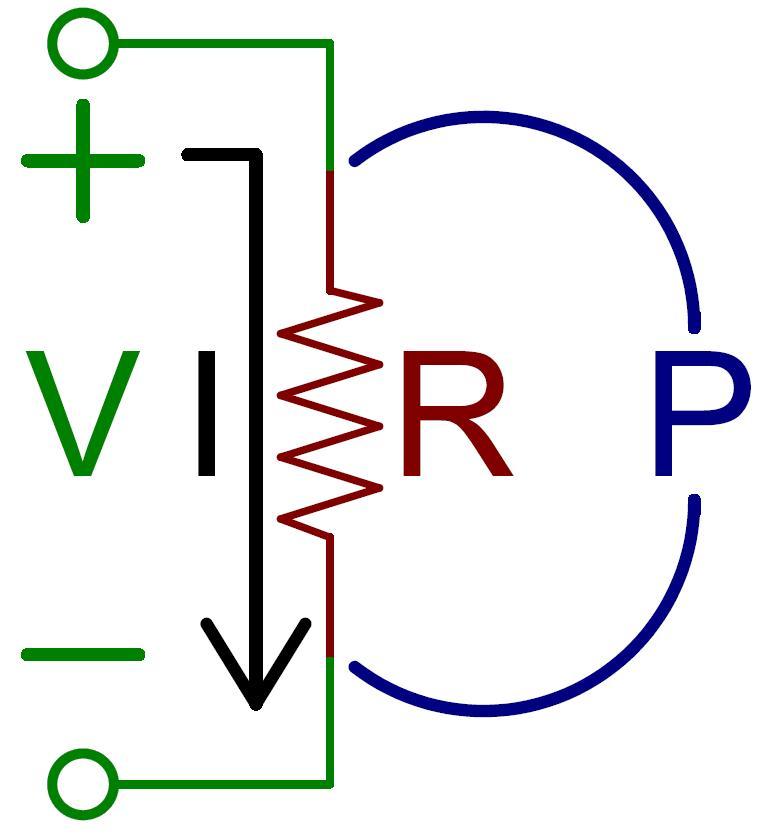
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Закон Ома для неоднородного участка цепи
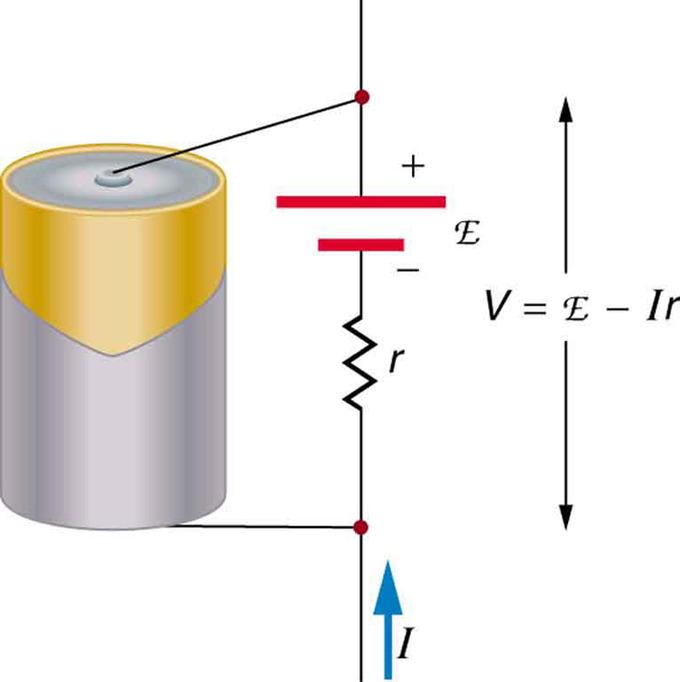
Физическая величина, равная отношению работы сторонних сил Aст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника Eэдс:
$ E_{эдс} = {A_{cт}over q} $ (1).
Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.
Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе Eэдс, действующей на данном участке. Поэтому полная работа равна:
$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).
Величина Uп называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
$ U_п = φ_1 – φ_2 $ (3).
Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
$ I = {U over R} $ (4).
Рис. 2. Портрет Георга Ома.
Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:
$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).
Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
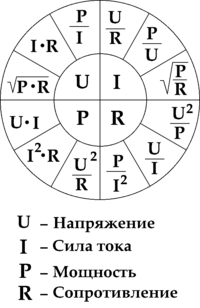
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Определение через разложение электрического поля
Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.
В показанной выше формуле Е — индуцированный — вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Единицы измерения в формуле
Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы
В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.
Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.
Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Вычисления напряжения в сети электричества
В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.
Что такое напряжение в сети электричества.
Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.
Показатель напряжения на вольтметре
За единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.
Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.
Чему равно напряжение.
Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.
Изображение вольтметра и электрической цепи
Напряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.
Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.
Формула закона Ома
Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.
Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.
Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению в сети и обратно пропорционально силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.
Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.
Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.
Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.
Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].
Как найти сопротивление нагрузки
Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.
Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.
Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.
Последовательное/параллельное соединения
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Как найти силу тока через сопротивление и напряжение
Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.
Мужчина считает силу тока
Существуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.
При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.
Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.
Источник
Физика: формула напряжения тока. Как найти и вычислить электрическое напряжение?
Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.
Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.
Единицы измерения в формуле
В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.
Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.
Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.
Как работает закон в реальной жизни
Формулу напряжения в физике иногда очень сложно понять. Более конкретным примером из реальной жизни является резервуар для воды со шлангом, идущим снизу. Жидкость представляет собой накопленный заряд. Требуется работа, чтобы наполнить бак водой. Это создает запас жидкости. Как разделение заряда в батарее. Чем больше ее в резервуаре, тем сильнее давление — и вода может выходить через шланг с большей энергией. Если бы в аквариуме было меньше жидкости, она вышла бы с минимальным количеством интенсивности.
Пример с обычной водой
Этот потенциал давления эквивалентен напряжению. Чем больше воды в баке, тем сильнее воздействие. Чем мощнее заряд хранится в батарее, тем выше напряжение.
Когда открываешь шланг, течет поток воды. Давление в резервуаре определяет, насколько быстро он вытекает. Электрический ток измеряется в амперах. Чем больше вольт, тем сильнее А тока. Значит, чем сильнее давление воды, тем быстрее она вытечет из бака.
Тем не менее ток также зависит от сопротивления. В случае шланга — это его ширина. Широкая труба позволяет пропускать больше воды за меньшее время, а узкая — противостоит потоку жидкости. С электрическим током также может быть сопротивление, измеренное в Омах.
По какой формуле определяется напряжение
Закон Ома гласит, что U равно текущему временному сопротивлению.
Если это 12-вольтовая батарея, то ее значение составляет два Ом, а ток составит шесть ампер. Если сопротивление было одним Ом, ток был бы 12 ампер.
Формула напряжения в физике гласит, что интенсивность, разница электрического потенциала и давления — это различие между двумя точками. Отличие в данном случае между двумя объектами (т. е. их напряжением) в статическом электрическом поле определяется как работа, необходимая на единицу заряда для перемещения испытательного резерва между точками. В Международной системе единиц полученный блок называется напряжением.
Различные используемые величины
В СИ работа выражается в джоулях на кулон, где 1 вольт = 1 джоуль за 1 кулон. Официальное определение СИ для вольта использует мощность и ток, где 1 вольт = 1 ватт (мощности) на 1 ампер (тока). Это определение эквивалентно более часто используемому «джоулю на кулон». Напряжение или разность электрических потенциалов обозначается символически DV, но чаще просто как V, например, в контексте Ома или Правилах Кирхгофа.
Различия электрического потенциала между точками могут быть вызваны зарядом, током через магнитное поле или некоторой комбинацией этих трех составляющих.
Вольтметр может быть использован для измерения напряжения (или разности потенциалов) между двумя точками в системе; часто в качестве одного объекта используется общий опорный потенциал, такой как заземление системы. Напряжение может представлять собой либо источник энергии (электродвижущая сила) либо потерянную, использованную или накопленную (падение потенциала) энергию.
Существует несколько полезных способов узнать какая формула напряжения в конкретном случае необходима.
Грубо говоря, сила определяется так, что отрицательно заряженные объекты притягиваются к более высоким напряжениям, а положительно — к более низким. Поэтому обычный ток в проводе или резисторе всегда течет от меньшего к большему.
Исторически формула закона напряжения упоминалась с использованием такого термина, как давление. Даже сегодня «натяжение» все еще применяется в таком контексте, например, в термине «высокое напряжение», которое обычно употребляется в электронике на основе термоэлектронных клапанов (вакуумных трубок).
Как найти напряжение, формула. Потенциал электрического поля
Увеличение напряжения с некоторой точки xA в какой-то момент xB дан кем-то.
В этой формуле для вычисления напряжения увеличение от точки A до B равно работе, которую нужно было бы выполнить за единицу заряда, против электрического поля, чтобы переместить частицу с A на B, не вызывая какого-либо ускорения. Математически это выражается как криволинейный интеграл от электрического поля вдоль этого пути. Согласно данному определению, разность напряжений между двумя точками не формируется однозначно, когда существуют изменяющиеся во времени магнитные поля, поскольку электрическая сила не является консервативной в таких случаях.
Если используется это определение напряжения, любая цепь, в которой существуют изменяющиеся во времени магнитные поля, например, ряды, содержащие индукторы, не будет иметь четко определенного напряжения между узлами в цепи. Однако если магнитные поля надлежащим образом содержатся в каждом компоненте, то электрическое является консервативным во внешней области, и составляющие хорошо определены в ней. В этом случае напряжение на индукторе, если смотреть со стороны, оказывается.
Несмотря на то, что внутреннее электрическое поле в катушке равно нулю (при условии, что это идеальный проводник). Существует еще несколько способов, чтобы узнать, какая формула напряжения необходима в конкретном случае.
Определение через разложение электрического поля
Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.
В показанной выше формуле Е — индуцированный — вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.
Еще один способ
Разберем формулу механического напряжения в физике, теории цепей.
В схемотехническом анализе и электротехнике сила на катушке индуктивности не считается нулевым или неопределенным, как предполагает стандартное определение. Это связано с тем, что инженеры-электрики используют модель с сосредоточенными элементами для представления и анализа цепей.
При этом предполагается, что в области окружающего ряда нет магнитных полей, и их влияние содержится в «сосредоточенных элементах», которые являются идеализированными и автономными составляющими схемы, используемыми для моделирования физических компонентов. Если предположение о незначительных утечках полей является слишком неточным, их эффекты могут быть смоделированы паразитными компонентами.
Однако в случае физического индуктора идеальное представление с сосредоточенными параметрами часто является точным. Это связано с тем, что поля утечки в индуктивности, как правило, незначительны, особенно если заряд представляет собой тороид. Если протекшие поля небольшие, можно найти, что является независимым от пути, и на клеммах индуктора имеется четко определенное напряжение. Это причина того, что измерения с помощью вольтметра на катушке часто в достаточной степени не зависят от расположения измерительных проводов.
Гидравлическая аналогия
Простая параллель для электрического контура в формуле изменения напряжения — вода, протекающая по замкнутому трубопроводу, приводимая в действие механическим насосом. Это можно назвать «водным контуром». Разность потенциалов между двумя точками соответствует отличием давлений между ними. Если насос создает перепад напора, то вода, текущая из одной колбы в другую, сможет выполнять работу, например, приводить турбину в движение. Точно так же работа может выполняться электрическим током, управляемым разностью потенциалов, обеспечиваемой батареей. Например, напряжение, которое достаточно заряжено автомобильным аккумулятором, может «проталкивать» большой ток через обмотки стартерного двигателя. Если насос не работает, он не создает разности давлений, и турбина не вращается. Аналогично если аккумуляторная батарея машины очень слаба или разряжена, то она не будет вращать стартер.
Гидравлическая аналогия является полезным способом понимания многих электрических концепций. В такой системе напряжение вычисляется по формуле давления, умноженного на объем перемещаемого заряда. В электрической цепи работа, выполняемая для передвижения частиц или других носителей, равна «электрическому давлению», умноженному на количество перемещенных электрочастиц. Чем больше перепад давления между двумя точками в отношении потока (разность потенциалов или перепад давления воды), тем больше расстояние между ними (электрический ток или поток воды).
Измерительные приборы
Инструментарий для определения напряжения включает в себя вольтметр, потенциометр и осциллограф. Первый работает путем измерения тока через фиксированный резистор, который, согласно закону Ома, пропорционален напряжению. Потенциометр работает путем балансировки неизвестного напряжения с известным в мостовой цепи. Катодно-лучевой осциллограф вычисляет, усиливая U и используя его для отклонения электронного луча от прямой траектории.
Типичные напряжения
Общий поток для батарей фонарика составляет 1,5 V. А совместное напряжение для автомобильных аккумуляторов — 12 вольт.
Общая сила, поставляемая большими энергокомпаниями потребителю, составляет от 110 до 120 вольт и от 220 до 240 вольт. Напряжения в передаче энергии, используемые для распределения всего тока от электростанций, может быть в несколько сотен раз больше, чем любые потребительские напряжения, как правило, от 110 до 1200 кВ (переменного тока).
Сила, которая используется в воздушных линиях для питания всех железнодорожных локомотивов, составляет от 12 кВ до 50 кВ (переменного тока) или от 1,5 кВ до 3 кВ (постоянного тока).
Потенциал Гальвани
Внутри проводящего материала на энергию электрона влияют не только средние возможности, но и конкретная тепловая и атомная среда, в которой он находится. Когда вольтметр подключен между двумя различными типами металла, он не измеряет разность электростатического потенциала.
Величина, измеренная с помощью вольтметра, является отрицательной и обычно называется разностью напряжений. В то время как чистая нескорректированная электростатическая возможность (неизмеряемая с помощью вольтметра) иногда называется Гальванической. Термины «напряжение» и «электрический потенциал» неоднозначны в том смысле, что на практике они могут относиться к любому из них в различных контекстах.
Источник
{I = dfrac{U}{R}}
На этой странице вы можете рассчитать силу тока, напряжение и сопротивление по закону Ома для участка цепи с помощью удобного калькулятора онлайн
Закон Ома – один из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Он был открыт эмпирическим путем Георгом Омом в 1826 году.
Содержание:
- калькулятор закона Ома
- закон Ома для участка цепи
- формула силы тока
- формула напряжения
- формула сопротивления
- примеры задач
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи I= dfrac{U}{R}
Формула силы тока
Формула позволяет найти силу тока I через напряжение U и сопротивление R по закону Ома для участка цепи.
{I = dfrac{U}{R}}
I – сила тока
U – напряжение
R – сопротивление
Сила тока (I) в проводнике прямо пропорциональна напряжению (U) на его концах и обратно пропорциональна его сопротивлению (R).
Формула напряжения
Формула позволяет найти напряжение U через силу тока I и сопротивление R по закону Ома для участка цепи.
{U = I cdot R}
U – напряжение
I – сила тока
R – сопротивление
Падение напряжение на проводнике равно произведению сопротивления проводника на силу тока в нем.
Формула сопротивления
Формула позволяет найти сопротивление R через силу тока I и напряжение U по закону Ома для участка цепи.
{R = dfrac{U}{I}}
R – сопротивление
U – напряжение
I – сила тока
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него.
Примеры задач на нахождение силы тока, напряжения и сопротивления по закону Ома
Задача 1
Найдите силу тока в участке цепи, если его сопротивление 40 Ом, а напряжение на его концах 4 В.
Решение
Воспользуемся формулой силы тока. Подставим в нее значения напряжения и сопротивления, после чего останется произвести простейший математический расчет.
I = dfrac{U}{R} = dfrac{4}{40} = 0.1 А
Ответ: 0.1 А
На этой странице есть калькулятор, который поможет проверить полученный ответ.
Задача 2
Найдите напряжение на концах нагревательного элемента, если его сопротивление 40 Ом, а сила тока 2А.
Решение
Для решения этой задачи нам пригодится формула напряжения.
U = I cdot R = 2 cdot 40 = 80 В
Ответ: 80 В
Проверим получившийся результат с помощью калькулятора .
Задача 3
Найдите сопротивление спирали, сила тока в которой 0.5 А, а напряжение на ее концах 120 В.
Решение
Чтобы найти сопротивление спирали нам потребуется формула сопротивления.
R = dfrac{U}{I} = dfrac{120}{0.5} = 240 Ом
Ответ: 240 Ом
Проверка .
Одним из самых фундаментальных терминов в электротехнике является термин «электрическое напряжение». В этой статье мы объясним, что это такое и как его рассчитать.
Объяснение простыми словами
Электрическое напряжение U является той самой причиной, которая «заставляет» протекать электрический ток I. Электрическое напряжение всегда возникает, когда заряды разделены друг от друга, то есть все отрицательные заряды на одной стороне, а все положительные — на другой. Если соединить эти две стороны электропроводящим материалом, потечет электрический ток.
Общепринятое определение термина «электрическое напряжение».
Электрическое напряжение (или просто напряжение) — это разность потенциалов между двумя точками в электрическом поле. Это движущая сила для электрического заряда.
Потенциал в электрическом поле — это энергия заряженного тела, не зависящая от его электрического заряда. Для пояснения вы можете посмотреть на сравнение с водяным контуром чуть ниже в статье.
Есть другое определение (из учебника по физике 8 класса):
Напряжение — это физическая велuчuна, характеризующая электрическое поле. Электрическое напряжение между двумя точками электрического поля численно равно работе, совершенной при переносе между ними заряда 1 Кл силами электрического поля.
Сравнение с использованием модели протекания воды.
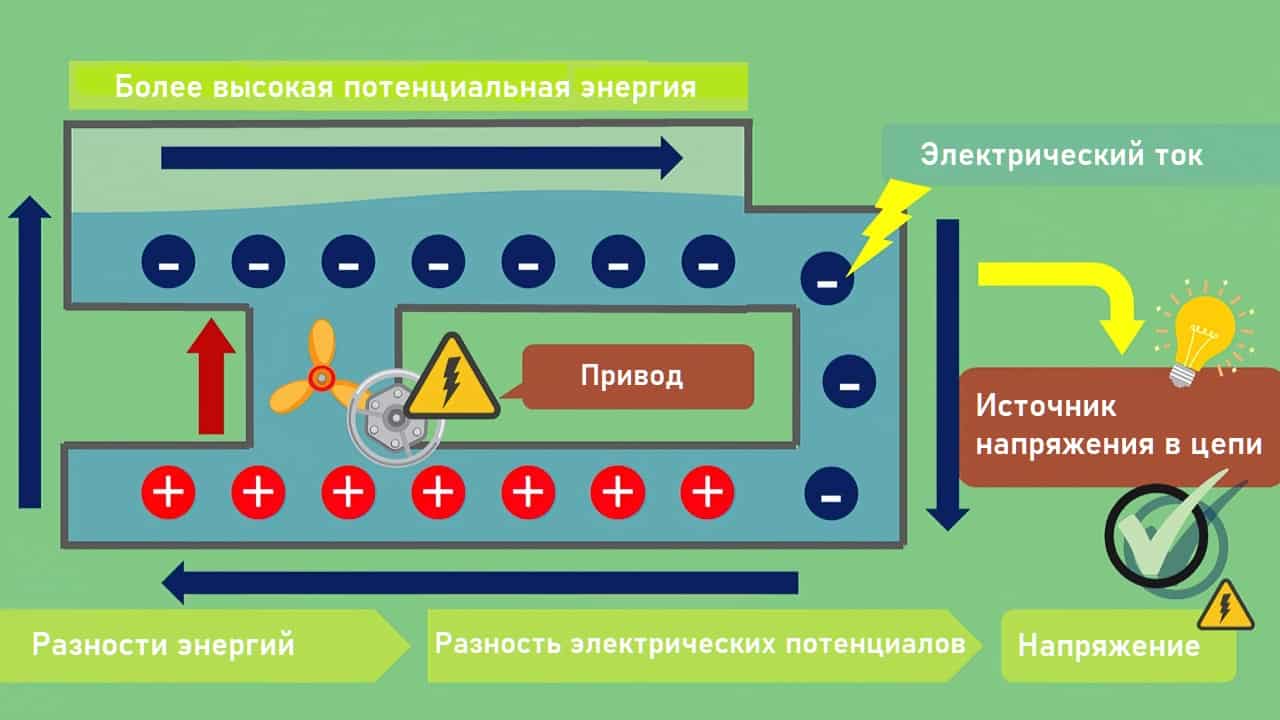
Хорошей аналогией, которая поможет вам представить себе электрическое напряжение и потенциал, является водяной контур. В этой схеме у вас есть два бассейна на разной высоте, которые соединены трубой. В этой трубе вода может перетекать из верхнего бассейна в нижний. Затем вода перекачивается обратно в верхний бассейн с помощью насоса, как показано на рисунке ниже.
В своих размышлениях вы теперь легко можете сравнить насос с источником электрического напряжения. Кроме того, поток воды можно сравнить с электрическим током. Насос транспортирует воду из нижнего бассейна в верхний. Оттуда она самостоятельно течет обратно в нижний бассейн. В данном примере насос является приводом для потока. Чем больше разница в высоте, тем сильнее поток. Решающим фактором является потенциальная энергия верхнего бассейна. Вы можете сравнить разность энергий двух бассейнов с разностью электрических потенциалов. Проще говоря, большая разница в высоте соответствует большему электрическому напряжению.
Формула
Формула для электрического напряжения U, согласно закона Ома для участка цепи, имеет вид
U = R * I .
Как видно из этой формулы, если электрическое напряжение остается неизменным, то чем больше электрическое сопротивление (R), тем меньше сила тока (I).
Другая формула для расчета электрического напряжения такова:
U = P / I .
То есть электрическое напряжение U равно мощности деленной на силу тока I.
Единица измерения электрического напряжения
Единицей измерения электрического напряжения в СИ является Вольт, сокращенно В (в честь итальянского учёного А. Вольта).
1 вольт (1 В) — это напряжение между двумя точками электрического поля, при переносе между которыми заряда 1 Кл совершается работа 1 Дж.
[U] = 1 В
Теперь вы можете объяснить смысл надписи 4,5 В или 9 В на круглой или плоской батарейке. Смысл в том, что при переносе с одного полюса источника на другой (через спираль лампочки или другой проводник) заряда 1 Кл силами электрического поля может быть совершена работа соответственно 4,5 Дж или 9 Дж.
В электротехнике напряжение может варьироваться от микровольт (1 мкВ = 1 * 10-6 В) и миливольт (1 мВ = 10-3 В), до киловольт (1 кВ = 1 * 103 В) и мегавольт (1 МВ = 106 В)
Вы можете преобразовать отдельные единицы измерения следующим образом:
1 В = 1000 мВ, 1 мВ = 1000 мкВ, 1 МВ = 1000 кВ, 1 кВ = 1000 В.
Электрическое напряжение в цепи
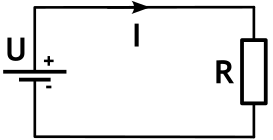
Для источников напряжения в схемах обычно используется один из следующих символов.
Источник напряжения всегда имеет два соединения/полюса. Полюс «плюс» и полюс «минус». Само напряжение обозначено стрелкой напряжения (UQ). Для источников оно всегда отображается от плюса к минусу.
Электрическое напряжение, падающее на резисторе, также можно обозначить стрелкой напряжения (на схеме обозначена как красная стрелка UR ). Это указывает на техническое направление электрического тока.
Также часто можно услышать термин «напряжение холостого хода» или «напряжение источника». Это выходное напряжение ненагруженного источника, т.е. источника, к которому ничего не подключено. Если цепь замкнута с нагрузкой, то можно измерить только напряжение на полюсах источника.
Электрические напряжения при последовательном и параллельном соединении
У нас уже есть статья о последовательном и параллельном соединении проводников, в котором мы обсуждаем эту тему более подробно. Поэтому здесь мы рассмотрим лишь некоторые основы.
При последовательном соединении компоненты подключаются в ряд.
Здесь электрическое напряжение источника делится на резисторы. Этот момент также описывается вторым правилом Кирхгофа. Здесь применимо следующее:
UQ = U1 + U2 + U3
то есть напряжение источника равно сумме электрических напряжений на отдельных резисторах. Напряжение источника по-разному распределяется по разным резисторам.
В электрической цепи с параллельным соединением компоненты расположены, соответственно, параллельно друг относительно друга. Это можно увидеть на следующей схеме.
Здесь гораздо проще определить электрические напряжения на резисторах, так как при параллельном соединении:
UQ = U1 = U2 = U3
Поэтому электрическое напряжение на резисторах такое же высокое, как и электрическое напряжение источника.
Измерение электрического напряжения
Приборы для измерения напряжения, также называемые вольтметрами, всегда подключаются параллельно потребителю, на котором необходимо измерить электрическое напряжение.
Одним из наиболее часто используемых вольтметров является цифровой мультиметр (DMM), поэтому мы покажем вам процедуру измерения напряжения с помощью DMM. Сначала необходимо установить тип электрического напряжения (DC — постоянный ток или AC — переменный ток).
Для постоянного тока необходимо обратить внимание на правильную полярность, т.е. подключить плюс к положительному полюсу. На следующем этапе необходимо выбрать правильный диапазон измерения. Если вы не можете оценить, насколько велика измеряемая величина, установите наибольший возможный диапазон и двигайтесь от него вниз, пока не найдете нужный. Наконец, вам нужно только «считать» электрическое напряжение прибором.
Примеры типовых значений электрического напряжения
Для некоторых применений соответствующее электрическое напряжение можно найти в таблице ниже.
| Светодиод | 1,2 — 1,5 В |
| Зарядное устройство USB | 5 В |
| Напряжение автомобильного аккумулятора | 12, 4 — 12,8 В |
| Напряжение в розетке (среднеквадратичное или действующее значение) | 230 В |
| Высоковольтные линии электропередач (ЛЭП) | 60 кВ — 1 МВ |
Вы можете видеть, что на высоковольтных линиях присутствует напряжение до мегавольт. Такие большие электрические напряжения используются для того, чтобы уменьшить потери в длинных линиях.
Решающим фактором для потребителя является мощность P, которую можно рассчитать для постоянного напряжения с помощью формулы:
P = U * I
Это означает, что электрический ток I так же важен для потребителя, как и электрическое напряжение. Согласно закону Ома, зависимость между током и напряжением имеет вид:
U = R * I .
Если напряжение остается неизменным, сопротивление определяет величину тока. Чтобы проиллюстрировать это, представьте следующее. У вас есть три разных бассейна, которые заполнены одинаковым количеством воды. Каждый бассейн имеет слив, который различается по сечению, т.е. в одном бассейне сливная труба очень маленькая, а в другом — очень большая.
Постоянное электрическое напряжение можно определить по тому, что все емкости заполнены на одинаковую высоту. Если слив узкий в нижней части, он представляет собой большое сопротивление. Ток здесь может течь только медленно. Если сечение сливной трубы больше, то сопротивление меньше и, соответственно, может протекать больший ток.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 июля 2020 года; проверки требуют 25 правок.
У этого термина существуют и другие значения, см. Напряжение.
| Напряже́ние | |
|---|---|
| U, V | |
| Размерность | L2MT-3I-1 |
| Единицы измерения | |
| СИ | вольт |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — скалярная физическая величина, значение которой численно равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B[1][2], деленной на величину этого заряда.
При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). Напряжение в общем случае формируется из вкладов двух работ: работы электрических сил 
и работы сторонних сил 
. Если на участке цепи не действуют сторонние силы (то есть 
), работа по перемещению включает только работу потенциального электрического поля (которая не зависит от пути, по которому перемещается заряд), и электрическое напряжение 
между точками A и B совпадает с разностью потенциалов между этими точками (поскольку 
). В общем случае напряжение между точками A и B отличается от разницы потенциалов между этими точками[3] на работу сторонних сил по перемещению единичного положительного заряда. Эту работу называют электродвижущей силой 
на данном участке цепи: 
Определение электрического напряжения можно записать в другой форме. Для этого нужно представить работу 
как интеграл вдоль траектории L, проложенной из точки A в точку B.
— интеграл от проекции эффективной напряжённости поля 
(включающего сторонние поля) на касательную к траектории L, направление которой в каждой точке траектории совпадает с направлением вектора 
в данной точке. В электростатическом поле, когда сторонних сил нет, значение этого интеграла не зависит от пути интегрирования и совпадает с разностью потенциалов.
Размерность электрического напряжения в Международной системе величин (англ. International System of Quantities, ISQ), на которой основана Международная система единиц (СИ), — L2MT-3I-1. Единицей измерения напряжения в СИ является вольт (русское обозначение: В; международное: V).
Понятие напряжение ввёл Георг Ом в работе 1827 года, в которой предлагалась гидродинамическая модель электрического тока для объяснения открытого им в 1826 году эмпирического закона Ома: 
.
Напряжение в цепях постоянного тока[править | править код]
Исторически принято, что направление тока совпадает с направлением движения положительных зарядов в проводнике (Б. Франклин).
Напряжение в цепи постоянного тока между точками A и B — работа, которую совершает электрическое поле при переносе пробного положительного заряда из точки A в точку B.
Напряжение может быть условно отрицательным, например, при двуполярном питании.
При однополярном источнике питания обычно «землёй» считают один из выводов источника, чаще отрицательный вывод.
Например, в автомобилях «землёй» принято читать корпус автомобиля, который соединяют с отрицательной (тонкой) клеммой свинцового аккумулятора (так было не всегда).
При двуполярном источнике за землю принимают его среднюю точку, соответственно появляется условно положительное напряжение, — от средней точки источника до плюсовой клеммы, и условно отрицательное — от средней точки до минусовой клеммы. Это условное соглашение называют «полярностью напряжения».
Напряжение в цепях переменного тока[править | править код]
Для описания цепей переменного тока применяются следующие напряжения:
- мгновенное напряжение;
- амплитудное значение напряжения;
- среднее значение напряжения;
- среднеквадратическое значение напряжения;
- средневыпрямленное значение напряжения.
Мгновенное напряжение есть разность потенциалов между двумя точками, измеренная в данный момент времени. Зависит от времени (является функцией времени):
Амплитудное значение напряжения есть максимальное по модулю значение мгновенного напряжения за весь период колебаний:
Для гармонических (синусоидальных) колебаний напряжения мгновенное значение напряжения выражается как:
Для сети переменного синусоидального напряжения со среднеквадратическим значением 220 В амплитудное напряжение равно приблизительно 311 В.
Амплитудное напряжение можно измерить с помощью осциллографа.
Среднее значение напряжения (постоянная составляющая напряжения) есть напряжение, определяемое за весь период колебаний, как:
Для синусоиды среднее значение напряжения равно нулю.
Среднеквадратическое значение напряжения (электротехнические наименования: действующее, эффективное) есть напряжение, определяемое за весь период колебаний, как:
Среднеквадратическое значение напряжения наиболее удобно для практических расчётов, так как на линейной активной нагрузке оно совершает ту же работу (например, лампа накаливания имеет ту же яркость свечения, нагревательный элемент выделяет столько же тепла), что и равное ему постоянное напряжение.
Для синусоидального напряжения справедливо равенство:
В технике и быту при использовании переменного тока под термином «напряжение» имеется в виду именно среднеквадратическое значение напряжения, и все вольтметры проградуированы, исходя из его определения. Однако конструктивно большинство приборов фактически измеряют не среднеквадратическое, а средневыпрямленное (см. ниже) значение напряжения, поэтому для несинусоидального сигнала их показания могут отличаться от истинного значения.
Средневыпрямленное значение напряжения есть среднее значение модуля напряжения:
Для синусоидального напряжения справедливо равенство:
На практике используется редко, однако большинство вольтметров переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала и проградуирована по среднеквадратическим значениям.
Напряжение в цепях трёхфазного тока[править | править код]
В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки относительно нейтрали, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в треугольник фазное напряжение равно линейному, а при соединении в звезду (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в 
раз больше фазного.
На практике напряжение трёхфазной сети обозначают дробью, в числителе которой стоит фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли), а в знаменателе — линейное напряжение. Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.
Характерные значения и стандарты[править | править код]
| Объект | Тип напряжения | Значение (на вводе потребителя) | Значение (на выходе источника) |
|---|---|---|---|
| Электрокардиограмма | Импульсное | 1—2 мВ | – |
| Телевизионная антенна | Переменное высокочастотное | 1—100 мВ | – |
| Гальванический цинковый элемент типа АА («пальчиковый») | Постоянное | 1,5 В | – |
| Литиевый гальванический элемент | Постоянное | 3—3,5 В (в исполнении пальчикового элемента, на примере Varta Professional Lithium, AA) | – |
| Логические сигналы компьютерных компонентов | Импульсное | 3,3 В; 5 В | – |
| Батарейка типа 6F22 («Крона») | Постоянное | 9 В | – |
| Силовое питание компьютерных компонентов | Постоянное | 5 В, 12 В | – |
| Электрооборудование автомобилей | Постоянное | 12/24 В | – |
| Блок питания ноутбука и жидкокристаллических мониторов | Постоянное | 19 В | – |
| Сеть «безопасного» пониженного напряжения для работы в опасных условиях | Переменное | 12—42 В | – |
| Напряжение наиболее стабильного горения свечи Яблочкова | Постоянное | 55 В | – |
| Напряжение в телефонной линии (при опущенной трубке) | Постоянное | 60 В | – |
| Напряжение в электросети Японии | Переменное трёхфазное | 100/172 В | – |
| Напряжение в домашних электросетях США | Переменное трёхфазное | 120 В / 240 В (сплит-фаза[en]) | – |
| Напряжение в бытовых электросетях России | Переменное трёхфазное | 220/380 В | 230/400 В |
| Разряд электрического ската | Постоянное | до 200—250 В | – |
| Контактная сеть трамвая и троллейбуса | Постоянное | 550 В | 600 В |
| Разряд электрического угря | Постоянное | до 650 В | – |
| Контактная сеть метрополитена | Постоянное | 750 В | 825 В |
| Контактная сеть электрифицированной железной дороги (Россия, постоянный ток) | Постоянное | 3 кВ | 3,3 кВ |
| Распределительная воздушная линия электропередачи небольшой мощности | Переменное трёхфазное | 6—20 кВ | 6,6—22 кВ |
| Генераторы электростанций, мощные электродвигатели | Переменное трёхфазное | 10—35 кВ | – |
| На аноде кинескопа | Постоянное | 7—30 кВ | – |
| Статическое электричество | Постоянное | 1—100 кВ | – |
| На свече зажигания автомобиля | Импульсное | 10—25 кВ | – |
| Контактная сеть электрифицированной железной дороги (Россия, переменный ток) | Переменное | 25 кВ | 27,5 кВ |
| Пробой воздуха на расстоянии 1 см | 10—20 кВ | – | |
| Катушка Румкорфа | Импульсное | до 50 кВ | – |
| Пробой слоя трансформаторного масла толщиной 1 см | 100—200 кВ | – | |
| Воздушная линия электропередачи большой мощности | Переменное трёхфазное | 35 кВ, 110 кВ, 220 кВ, 330 кВ | 38 кВ, 120 кВ, 240 кВ, 360 кВ |
| Электрофорная машина | Постоянное | 50—500 кВ | – |
| Воздушная линия электропередачи сверхвысокого напряжения (межсистемные) | Переменное трёхфазное | 500 кВ, 750 кВ, 1150 кВ | 545 кВ, 800 кВ, 1250 кВ |
| Трансформатор Тесла | Импульсное высокочастотное | до нескольких МВ | – |
| Генератор Ван де Граафа | Постоянное | до 7 МВ | – |
| Грозовое облако | Постоянное | От 2 до 10 ГВ | – |
См. также[править | править код]
- Источник напряжения
- Список параметров напряжения и силы электрического тока
- Закон Пашена
Примечания[править | править код]
- ↑ Миллер М. А., Пермитин Г. В. Напряжение электрическое // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 244—245. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Напряжение электрическое / Юрьев Ю. В. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. — 1977. — Т. 2.
Литература[править | править код]
- Миллер М. А., Пермитин Г. В. Напряжение электрическое // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 244—245. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- Детлаф А. А., Яворский Б. М., Милковская Л. Б.. Курс физики. Электричество и магнетизм. — М.: “ВЫСШАЯ ШКОЛА”, 1977. — Т. 2.
Ссылки[править | править код]
- Электрическое напряжение // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Про разность потенциалов, электродвижущую силу и напряжение
- «Глоссарий.ру»: Словарь по естественным наукам.
