У этого термина существуют и другие значения, см. Объём (значения).
| Объём | |
|---|---|
 |
|
| Размерность | L3 |
| Единицы измерения | |
| СИ | м3 |
| СГС | см3 |
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей[1].
Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма[править | править код]
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.
Математически[править | править код]
Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром 

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Сводка формул[править | править код]
| Форма тела | Формула для вычисления объёма | Обозначения |
|---|---|---|
| Куб | 
|

|
| Прямоугольный параллелепипед | 
|

|
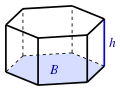
| Призма
(B: площадь основания) |

|
|
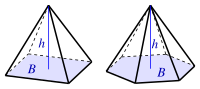
| Пирамида
(B: площадь основания) |

|
|
| Параллелепипед | 
|

|
| Тетраэдр | 
|

|
| Шар | 
|

|
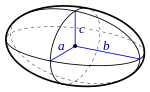
| Эллипсоид | 
|
|
| Прямой круговой цилиндр | 
|

|
| Конус | 
|

|
| Тело вращения | 
|

|
Через плотность[править | править код]
Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: 
Единицы объёма жидкости[править | править код]
- 1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские[2][править | править код]
- Ведро = 12,3 литра
- Бочка = 40 вёдер = 492 литра
Английские[править | править код]
- 1 пинта = 0,568 литра
- 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
- 1 галлон = 8 пинтам = 4,55 литра
- 1 галлон (амер.) = 3,785 литра
Античные[править | править код]
- Котила = 0,275 литра
Немецкие[править | править код]
- Шоппен
Древнееврейские[3][править | править код]
- Эйфа = 24,883 литра
- Гин = 1/6 эйфы = 4,147 литра
- Омер = 1/10 эйфы = 2,4883 литра
- Кав = 1/3 гина = 1,382 литра
Единицы объёма сыпучих веществ[править | править код]
Русские[править | править код]
- Четверик = 26,24 литра (1 пуд зерна)
- Гарнец = 3,28 литра
- Четверть = 1/4 ведра = 3,075 литра
- Штоф = 1/8 ведра = 1,54 литра
- Кружка = 1/10 ведра = 1,23 литра
- Бутылка (винная) = 1/16 ведра = 0,77 литра
- Бутылка (пивная) = 1/20 ведра = 0,61 литра
- Чарка = 1/10 кружки = 0,123 литра
- Шкалик (косушка) = 1/2 чарки = 0,0615 литра
Английские[править | править код]
- 1 бушель = 8 галлонов = 36,36872 литра
- 1 баррель = 163,65 литра
Прочие единицы[править | править код]
- 1 унция (англ.) = 2,841⋅10−5 м³
- 1 унция (амер.) = 2,957⋅10−5 м³
- 1 кубический дюйм = 1,63871⋅10−5 м³
- 1 кубический фут = 2,83168⋅10−2 м³
- 1 кубический ярд = 0,76455 м³
- 1 кубическая астрономическая единица =3,348⋅1024 км³
- 1 кубический световой год = 8,466⋅1038 км³
- 1 кубический парсек = 2,938⋅1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅1049 км³
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1982, с. 1149.
- ↑ Меры объёма в Древней Руси. Дата обращения: 17 ноября 2013. Архивировано 14 июля 2014 года.
- ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4
Литература[править | править код]
- Объём // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020. Архивировано 24 ноября 2020 года.
Измерение объёма тела по формуле — возможные способы, единицы измерения
Содержание:
- Понятие объема тела
- Свойства объема тела
- Как вычислить объем тела: все формулы
- Примеры решения задач
- Задания для самостоятельной работы
Понятие объема тела
Объем является количественным параметром пространства, занятого телом или веществом.
Термин объема можно рассматривать совместно с понятием вместимости. Это обозначение для объема какого-то внутреннего пространства сосуда, коробки и тому подобного. Объем тела, как и вместимость некой емкости, зависит от таких характеристик, как:
- форма;
- линейные размеры.
Главным свойством объема принято считать аддитивность.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Аддитивность означает равенство объема какого-либо тела сумме объемов частей этого тела, которые не пересекаются между собой.
Согласно СИ, единицей измерения объема является метр кубический (м³). В процессе решения задач можно встретить единицы измерения объемов тел в виде см³, дм³, или литров. В иностранной литературе также используются указания объемов веществ, находящихся в жидком или сыпучем состоянии, в таких единицах измерения, как, например, галлон, баррель и другие.
Величина объема используется при составлении различных уравнений и неравенств. При этом данный параметр обозначают с помощью буквы V. Это сокращение от латинского слова volume, которое в переводе означает объем или наполнение.
Свойства объема тела
В процессе решения разнообразных задач по физике, алгебре и геометрии целесообразно использовать свойства, которыми обладает объем тела. Перечислим основные из них:
- Объем тела не может быть отрицательной величиной.
- В том случае, когда некое геометрическое тело состоит из определенного количества геометрических тел, не обладающих едиными внутренними точками, объем такого тела складывается из объемов составляющих его тел.
- Объем фигуры в виде куба с ребром, значение которого равно единице измерения длины, равен единице.
- Аналогичные друг другу геометрические тела обладают одинаковыми объемами.
- В том случае, когда тело имеет объем V1 и расположено в другом теле с объемом V2, справедливо следующее соотношение: (V1<V2
).
Как вычислить объем тела: все формулы
Существует практический способ определения объема тела, включая тела, обладающие сложной формой и геометрией. Данная методика основана на законе Архимеда и предполагает погружение рассматриваемого тела в некую жидкость. По результатам следует измерить объем вытесненной телом жидкости. Данная величина равна объему измеряемого тела.
Формула расчета объема тела, исходя из известных величин массы и плотности:
(V={frac {m}{rho }})
Здесь m определяется, как масса, а rho является средней плотностью тела.
В том случае, когда тела обладают простыми геометрическими формами, в решении задач допустимо использовать специальные формулы. К примеру, для того чтобы найти объем куба, ребро которого равно а, следует применить такую формулу: (V=a^{3}).
Вычислить объем некого прямоугольного параллелепипеда можно путем умножения длины, ширины и высоты. Запишем другие распространенные формулы для расчета объемов геометрических фигур:
- куб, формула объема: (V=a^{3}):
- прямоугольный параллелепипед, формула объема: (V=abc) (произведение длин трех сторон):
- призма, формула объема: ( V=Bh) (произведение площади основания и высоты):
- пирамида, формула объема: (V={frac {1}{3}}Bh:)
- параллелепипед, формула объема: (V=abc{sqrt {K}}, {begin{aligned}K=1&+2cos(alpha )cos(beta )cos(gamma )\&-cos ^{2}(alpha )-cos ^{2}(beta )-cos ^{2}(gamma )end{aligned}}:
) -
- тетраэдр, формула объема: (V={{sqrt {2}} over 12}a^{3}:)
- шар, формула объема: (V={frac {4}{3}}pi r^{3}):
- эллипсоид, формула объема: (V={frac {4}{3}}pi abc):
- прямой круговой цилиндр, формула объема: (V=pi r^{2}h):
- конус, формула объема: (V={frac {1}{3}}pi r^{2}h):
- тело вращения, формула объема: (V=pi cdot int _{a}^{b}f(x)^{2}mathrm {d} x):
В том случае, когда необходимо определить объем, которым обладает некое тело, имеющее сложную форму, нужно разбить мысленно данное тело на отдельные части. Такие части целого должны иметь простую форму. Далее следует сложить вычисленные объемы простых тел. Результат будет являться значением объема начального тела.
Примеры решения задач
Задача 1
Задача
Имеется пара шаров. Радиус первого шара в 5 раз превышает радиус второго шара.
Требуется определить, во сколько раз площадь поверхности второго шара меньше по сравнению с площадью поверхности первого шара
Решение
Рассчитать площадь поверхности можно по формуле:
(S=4pi R^2)
Тогда запишем отношения площадей пары шаров:
(dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2})
Сравним радиусы геометрических фигур:
(R_1=5R_2)
В результате:
(dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их (K_1) и (K_2).
Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.
Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).
Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
(S=pi R (R+l))
Запишем отношения площадей полной поверхности заданных конусов:
(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})
Согласно условию задачи, имеем:
(R_1=4l_1, R_2=frac12R_1=2l_1)
В результате:
(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)
Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})
Известно, что:
(a_1=7a_2, b_2=2b_1, c_1=3c_2)
В результате:
(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)
Ответ: 10.
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Решение
Составим формулу для расчета площади боковой поверхности конуса:
(S=pi Rl)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)
Ответ: 0,2.
Задача 5
Имеется пара шаров. Объем первой фигуры составляет 54. Радиус второй фигуры в 3 раза меньше по сравнению с радиусом первой. Нужно определить объем второго шара.
Решение
Запишем формулу, согласно которой можно определить объем шара:
(V=dfrac43 pi R^3)
Составим отношение объемов двух фигур:
(dfrac{54}{V_2}=dfrac{V_1}{V_2}= dfrac{frac43 pi ,R_1^3}{frac43 pi ,R_2^3}=left(dfrac{R_1}{R_2}right)^3)
По условиям задачи:
(R_1=3R_2)
В результате:
(dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad V_2=dfrac{54}{27}=2)
Ответ: 2.
Задача 6
Имеется некая емкость конусообразной формы. Ее заполнили до половины с помощью 75 гр жидкости. Необходимо вычислить вес жидкости, которую нужно добавить в емкость, чтобы заполнить ее до верхнего края.
Решение
Вспомним формулу объема из курса физики:
(V=frac{m}{rho})
Предположим, что O является центром основания большего конуса. Пусть Q — центр основания меньшего конуса, а S обозначает общую вершину данных фигур. В одной плоскости построим радиусы OA и QB:
В таком случае:
(QBparallel OA)
(triangle SQBsim triangle SOA)
В результате:
(dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21)
Получим, что:
(m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho= dfrac13cdot picdot QScdot QB^2 cdot rho)
Можно сделать вывод, что:
(m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho= dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
Таким образом, потребуется долить в емкость:
(600-75=525 {small{text{грамм}}})
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой.
Исследуем плоскость ASO. Построим (A’Hparallel SO), где SO представляет собой высоту начальной фигуры. В таком случае:
(A’Hperp ABC)
В результате получилось расстояние, которое равно (frac13SO:)
(triangle AA’Hsim triangle ASO)
(dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad SA=3AA’ quadRightarrowquad SA’=dfrac23SA)
Таким образом:
(SQ=frac23SO)
(triangle ASBsim triangle A’SB’)
Получим, что:
(dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad A’B’=dfrac23AB)
Запишем отношения объемов пирамид:
(dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}= dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot AB^2}=dfrac{SQ}{SO}cdot left(dfrac{A’B’}{AB}right)^2=dfrac23cdot left(dfrac23right)^2=dfrac8{27})
В результате объем малой фигуры составит:
(V_{{small{text{м}}}}=dfrac8{27}cdot 54=16)
Ответ: 16.
Задания для самостоятельной работы
Задание 1
Имеется пара конусов. Вторая фигура обладает радиусом, который в три раза больше по сравнению с радиусом первой фигуры. Второй конус выше первого в шесть раз. Объем второй фигуры равен 18. Требуется вычислить, чему равен объем первого конуса.
Решение
Формула определения объема конуса:
(V=frac13pi R^2h)
Запишем отношения объемов двух фигур:
(dfrac{V_1}{18}=dfrac{V_1}{V_2}= dfrac{frac13pi ,R_1^2,h_1}{frac13 pi ,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot dfrac{h_1}{h_2})
Исходя из условий задачи:
(R_2=3R_1)
(h_1=6h_2)
В результате:
(dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}= dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot 18=12)
Ответ: 12
Задание 2
Дано два шара. Объем первого шара в 343 раза больше по сравнению с объемом второго шара. Нужно вычислить, во сколько раз радиус первой фигуры больше, чем радиус второй фигуры.
Решение
Запишем формулу для нахождения объема шара:
(V=dfrac43 pi R^3)
Составим отношения объемов данных шаров:
(dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}= left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
(S=2pi RH)
Составим отношение площадей боковых поверхностей двух фигур:
(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})
В результате:
(R_2=4R_1, H_1=5H_2)
Таким образом:
(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)
Получим, что:
(S_2=dfrac{16cdot 4}5=12,8)
Ответ: 12,8.
Задание 4
Имеется некая емкость конусообразной формы. Объем этой емкости составляет 2700 мл. Требуется рассчитать количество жидкости, налитой в емкость, если ее уровень в 3 раза меньше по сравнению с высотой емкости.
Решение
Введем обозначения, как на рисунке:
В таком случае:
(QBparallel OA и triangle SQBsim triangle SOA)
Таким образом:
(dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13)
Соотношение объемов жидкости до определенной линии и емкости:
(dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}= dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27})
В результате:
(V_{small{text{ж}}}=dfrac1{27}V=100)
Ответ: 100.
Задача 5
На рисунке изображены фигуры в виде шаров. Первый шар имеет радиус 6. Второй шар имеет радиус 2. Нужно вычислить, во сколько раз объем первой фигуры превышает объем второй фигуры.
Решение
Запишем формулу для расчета объема шара, который не может изменяться:
(V=dfrac43 pi R^3)
Составим отношение объемов двух шаров:
(dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}= left(dfrac62right)^3=27)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.
Kiru
Ученик
(226)
2 дня назад
Да, в физике есть формула для вычисления объёма различных тел. Формула для объёма зависит от формы тела. Например, для параллелепипеда объём вычисляется по формуле:
V = a × b × h,
где a, b и h – длина, ширина и высота соответственно.
Для сферы объём вычисляется по формуле:
V = (4/3) × π × r³,
где r – радиус сферы.
Для цилиндра объём вычисляется по формуле:
V = π × r² × h,
где r – радиус основания цилиндра, h – высота.
стас прачкис
Гуру
(3765)
2 дня назад
Учительница права. Физика занимается изучением физических Явлений. Объëм это просто число, получение в результате арифметических вычислений. А арифметика не является физическим явлением.
К примеру Сила Тока так же просто число, получение в результате арифметических вычислений. Вот Напряжение есть, потому что благодаря этому явлению возникает электрический ток. Сопротивление существует потому, что оно обусловлено свойствами вещества. А Сила Тока просто число, а не явление.
Физика всегда обращается к Математике, чтобы узнать количество того, или иного явления.
Поэтому чтобы хорошо решать задачи по физике, необходимо учится математическим преобразованиям и вычислениям.
Как найти объем тела?
Объем (V) физического тела любой формы можно определить, если знать его массу (m) и среднюю плотность материала (p) — эти две величины надо перемножить: V=m∗p.
Как найти объем с помощью воды?
V = πr2h, где π ≈ 3,14; r – радиус цилиндра; h – расстояние между двумя метками. Посредством этой формулы вы вычислите объем вытесненной воды, а значит и объем тела.
Как найти объем по весу?
Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.
Чему равен объем погруженной части тела?
= m ⋅ g = ρ тела ⋅ V всего тела ⏟ ∥ m ⋅ g . Отношение объёма погруженной части тела к полному объёму тела равно отношению плотности тела к плотности жидкости.
Как найти объем в физике 7 класс?
Объём тела вычисляют по формулам: Для прямоугольного параллелепипеда: объём = длина ⋅ ширина ⋅ высота . Если длина равна l 1 , ширина l 2 , высота l 3 , тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3 .
Как найти массу тела по его весу?
Получится m = P/g. Подставьте известные значения: m = 549/9,8 = 56 кг. Вы решили задачу. Ответ: масса тела, которое весит 549 Н (на поверхности Земли) равна 56 кг, или m = 56 кг.
Как определить объем погруженного тела?
Согласно закону Архимеда, объем тела, погруженного в воду равен объему вытесненной им воды. Чтобы определить таким образом объем цилиндра, нужно взять мерный стакан с водой со шкалой объема. Определить по шкале первоначальный объем воды — V1. Затем погружаем цилиндр в воду и отмечаем объем воды после погружения — V2.
Как найти вес и массу?
1 Часть 1 из 4: Вычисление веса
- Так как вес является силой, X Источник информации эту формулу можно записать и как F = mg.
- P или F — соответственно, вес или сила (измеряется в ньютонах, Н).
- m — масса тела (измеряется в килограммах, кг).
- g — ускорение свободного падения (измеряется в метрах на секунду в квадрате, м/с2).
Как найти вес жидкости формула?
Вес тела направлен вниз. Архимедова сила: F А = m ж ⋅ g . Сила направлена вверх. Вес тела в жидкости: P 1 = P − F А = mg − m ж g .
Что такое выталкивающая сила 4 класс?
На тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объёме погружённой части тела. Эта выталкивающая сила и называется силой Архимеда. У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.
Чему равна выталкивающая сила?
Закон Архимеда: Выталкивающая сила равна силе тяжести жидкости (или газа) вытесненной телом.
Как определить объем 7 класс?
Объём тела вычисляют по формулам: Для прямоугольного параллелепипеда: объём = длина ⋅ ширина ⋅ высота . Если длина равна l 1 , ширина l 2 , высота l 3 , тогда объём будет V = l 1 ⋅ l 2 ⋅ l 3 .
Как найти объем по формуле?
Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани. = 30.
Как найти вес подвижного тела?
P=m(g-a) — вес тела в случае, когда вектор ускорения совпадает по направлению с вектором ускорения свободного падения. В этом случае сила веса по модулю меньше силы тяжести.
Как найти массу зная вес и объём?
Исходя из определения, d=m/V, гдеm – масса предмета (кг),V — его объем (м3). Как видно из формулы, плотность вещества – это масса единицы его объема. 3.
Как найти объем цилиндра?
Чтобы определить объем цилиндра по радиусу, необходимо произвести расчет по формуле:
- V = π·r²·h.
- π — константа равная (3.14);
В чем измеряется объем?
| Объём | |
|---|---|
| Размерность | L3 |
| Единицы измерения | |
| СИ | м3 |
| СГС | см3 |
).
 2}=25)
2}=25)
Таким образом, первый шар имеет площадь поверхности, которая в 25 раз больше по сравнению с аналогичной характеристикой второго шара.
Ответ: 25.
Задача 2
На рисунке изображены конусы. Назовем их (K_1) и (K_2).
Полная поверхность (K_1) по площади относится к площади полной поверхности (K_2) как 4:1.
Фигура (K_1) обладает радиусом, который в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2).
Требуется вычислить, как относится образующая (K_2) к образующей (K_1.)
Источник: shkolkovo.net
Решение
Представим, что образующая конуса равна 1, а радиус основания обозначим, как R. Тогда можно записать следующее соотношение:
(S=pi R (R+l))
Запишем отношения площадей полной поверхности заданных конусов:
(dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)})
Согласно условию задачи, имеем:
(R_1=4l_1, R_2=frac12R_1=2l_1)
В результате:
(dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)} quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5)
Ответ: 0,5.
Задача 3
Даны два прямоугольных параллелепипеда. Объем первой фигуры равен 105. Известно, что первый параллелепипед по высоте превышает второй в 7 раз. Ширина второй фигуры в 2 раза больше по сравнению с аналогичным параметром первой фигуры. Первый параллелепипед длиннее в три раза, чем второй. Необходимо вычислить объем, который имеет второй параллелепипед.
Источник: shkolkovo.net
Решение
Обозначим высоту, ширину и длину геометрических фигур с помощью букв а, b, с соответственно. Вспомним формулу, по которой можно найти объем прямоугольного параллелепипеда:
V=abc
Применительно к нашей задаче, запишем:
(dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2})
Известно, что:
(a_1=7a_2, b_2=2b_1, c_1=3c_2)
В результате:
(dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}= dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot 2}{21}=10)
Ответ: 10.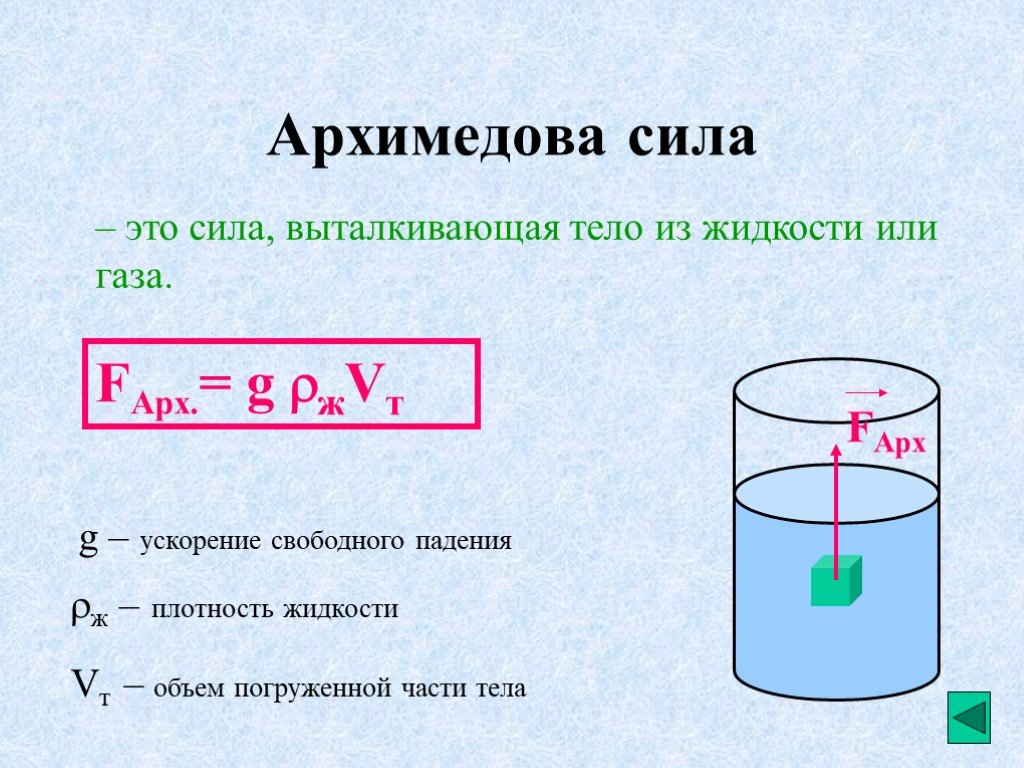
Задача 4
Даны два конуса. Площадь боковой поверхности первой геометрической фигуры относится к площади боковой поверхности второй фигуры как 3:7. Первый конус обладает радиусом, который относится к радиусу второго конуса, как 15:7. Необходимо определить, как относится образующая первого конуса к образующей второго конуса.
Источник: shkolkovo.net
Решение
Составим формулу для расчета площади боковой поверхности конуса:
(S=pi Rl)
Запишем отношения площадей боковых поверхностей для первого и второго конусов:
(dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2})
Зная, что отношение радиусов двух геометрических фигур равно 15:7, получим:
(frac{R_1}{R_2}=frac{15}7, то dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2)
Ответ: 0,2.
Задача 5
Имеется пара шаров.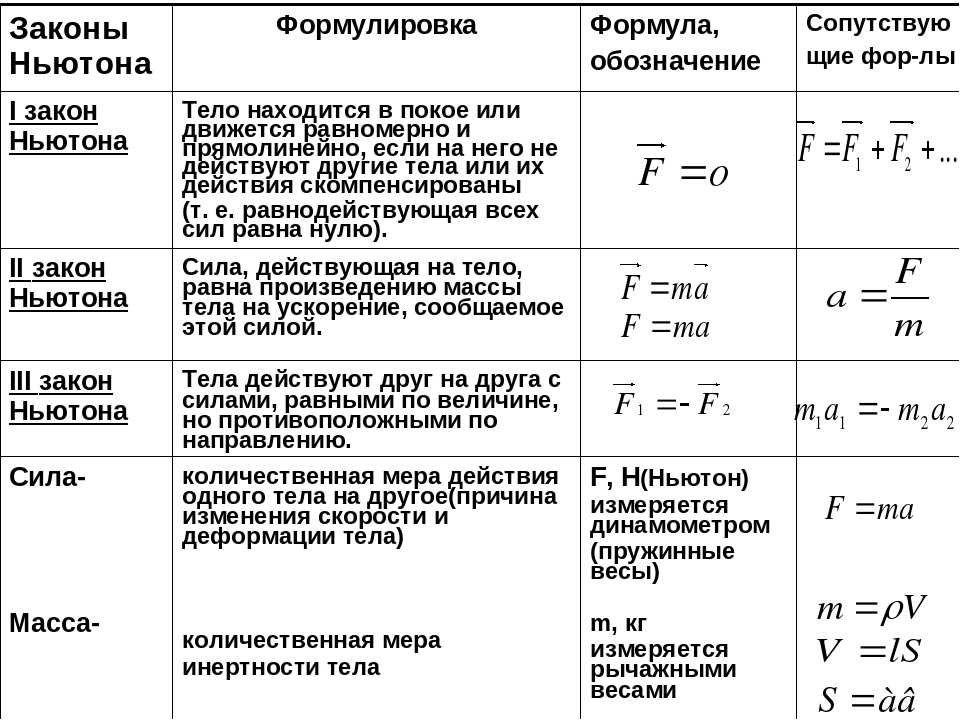 2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
2cdot rhoright)=8cdot 75=600 {small{text{грамм}}})
Таким образом, потребуется долить в емкость:
(600-75=525 {small{text{грамм}}})
Ответ: 525.
Задача 7
Изображена четырехугольная пирамида. Ее высота равна h. Отметим точку сбоку на ребре геометрической фигуры так, чтобы она была удалена на frac13h от плоскости основания. Данную точку пересекает плоскость, которая параллельна плоскости основания и отделяет от пирамиды аналогичную фигуру меньшего размера. Объем начальной пирамиды равен 54. Требуется вычислить объем меньшей пирамиды, которая получилась в результате.
Источник: shkolkovo.net
Решение
Назовем точку, через которую проведена плоскость, A’ на ребре AS. Параллельность плоскости и основания является причиной пересечения боковых граней по прямым A’B’, B’C’, C’D’, D’A’, параллельным соответственно AB, BC, CD, DA. В этом случае SA’B’C’D’ является правильной четырехугольной пирамидой. 3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
3 quadRightarrowquad dfrac{R_1}{R_2}=sqrt[3]{343}=7)
Сделаем вывод, что радиус первого шара в 7 раз больше по сравнению с радиусом второго шара.
Ответ: 7.
Задание 3
На рисунке изображены два цилиндра. Первый из них обладает площадью боковой поверхности, равной 16. Радиус второй фигуры больше в 4 раза по сравнению с радиусом первой фигуры. Второй цилиндр ниже, чем первый цилиндр, в 5 раз. Требуется вычислить площадь боковой поверхности второго цилиндра.
Источник: shkolkovo.net
Решение
Запишем формулу для вычисления площади боковой поверхности цилиндра, которую уже проходили ранее:
(S=2pi RH)
Составим отношение площадей боковых поверхностей двух фигур:
(dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}= dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2})
В результате:
(R_2=4R_1, H_1=5H_2)
Таким образом:
(dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}= dfrac14cdot 5=dfrac54)
Получим, что:
(S_2=dfrac{16cdot 4}5=12,8)
Ответ: 12,8.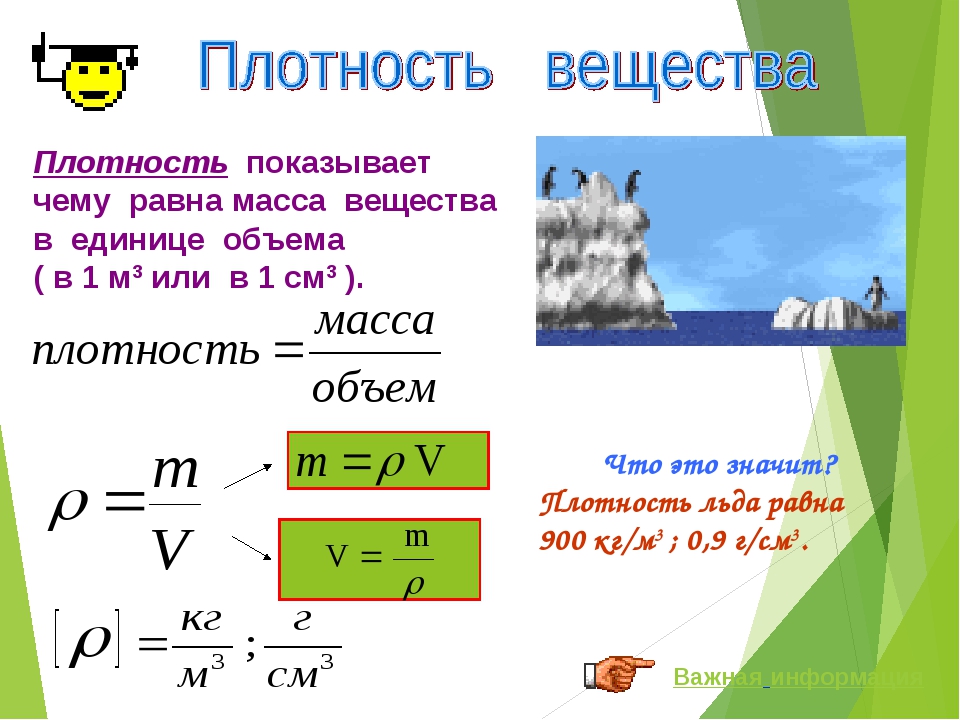 3=27)
3=27)
В результате объем первого шара в 27 раз больше по сравнению с объемом второго шара.
Ответ: 27.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки
Научим применять физические формулы для решения задач
Начать учиться
409.8K
Готовясь к экзаменам, удобно иметь под рукой шпаргалку, где будет кратко изложено самое важное. В этом материале мы объединили все основные формулы по физике за 7 класс с пояснениями и терминами. Их можно скачать на свой компьютер, чтобы всегда иметь под рукой.
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Полезные подарки для родителей
В колесе фортуны — гарантированные призы, которые помогут наладить учебный процесс и выстроить отношения с ребёнком!
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины.
Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения.
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
-
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
-
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
-
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.

-
Траектория движения — мысленная линия, вдоль которой перемещается тело.
-
Путь — длина траектории тела от начальной до конечной точки.
-
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
-
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние.
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.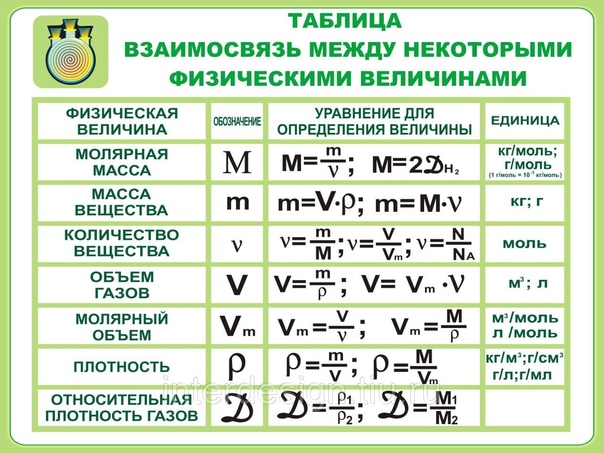
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес.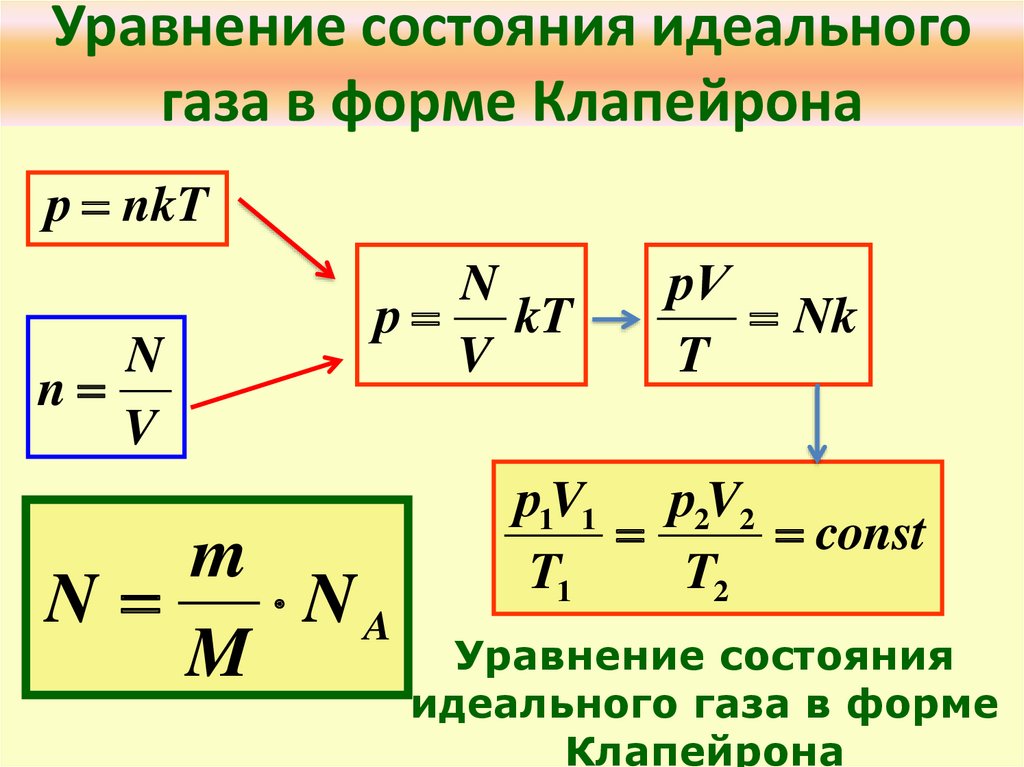
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз.
Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l.
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.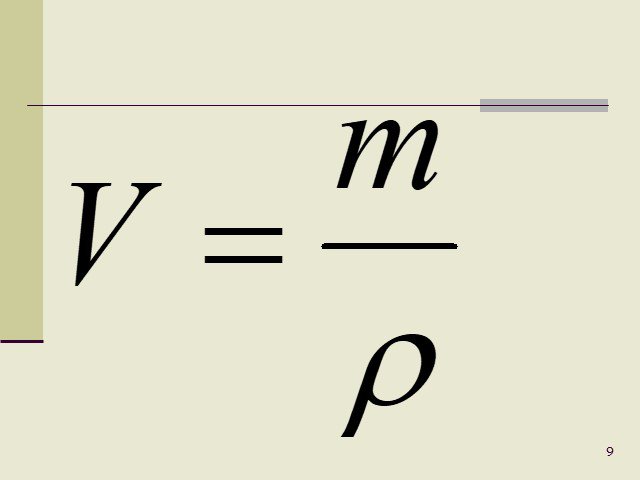
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.
Сила давления направлена перпендикулярно поверхности.
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.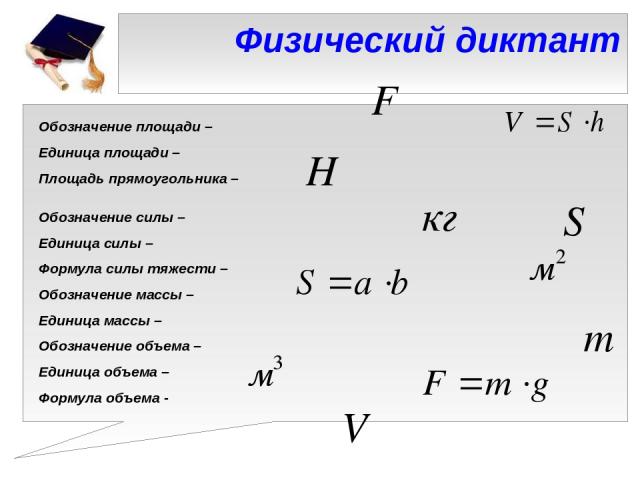
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
-
если плотность тела выше плотности среды, оно уйдет на дно;
-
если плотность тела ниже, оно всплывет на поверхность.

Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение.
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
-
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
-
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.

Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
|
Кинетическая энергия |
Пропорциональна массе тела и квадрату его скорости. |
Ek = mv2/2 |
|
Потенциальная энергия |
Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. |
Ep= mgh |
|
Полная механическая энергия |
Складывается из кинетической и потенциальной энергии. |
E = Ek+Ep |
|
Сохранение и превращение энергии |
Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. |
Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!
Яна Кононенко
К предыдущей статье
Закон Джоуля-Ленца
К следующей статье
Диффузия
Получите индивидуальный план обучения физике на бесплатном вводном уроке
Премиум
На вводном уроке с методистом
-
Выявим пробелы в знаниях и дадим советы по обучению
-
Определим уровень и подберём курс
-
Расскажем, как
проходят занятия
Формулы объема — объяснение, единицы измерения, примеры решений и часто задаваемые вопросы
- Формула
- Формула объема
Что такое объем?
Дата последнего обновления: 17 апреля 2023 г.
•
Всего просмотров: 237,6 тыс.
•
Просмотров сегодня: 3,07 тыс.
как объем предмета. Кроме того, если объект полый, то известно, что его внутренняя часть пуста. Полая часть может быть заполнена воздухом или жидкостью. В этом случае объем вещества, которым можно заполнить внутреннее пространство, даст вместимость любой емкости.
Таким образом, объем объекта может быть определен как мера занимаемого им пространства, или объем объекта как объем вещества, которое может вместить его внутренняя часть. Здесь единицей измерения любого из двух является кубическая единица.
Единицы объема
Объем измеряется в «кубических» единицах. Объем любой заданной фигуры — это количество кубиков, необходимых для ее полного заполнения, например, кубиков в коробке.
Объем куба равен сторона х сторона х сторона. Поскольку все стороны квадрата равны, это может быть просто длина одной стороны в кубе.
Если предположить, что у квадрата одна сторона равна 4 дюймам, объем будет 4 дюйма умножить на 4 дюйма x 4 дюйма, или 64 кубических дюйма. (Кубические дюймы также могут быть записаны в 3.)
Некоторые формулы для нахождения объемов основных геометрических фигур: 0048
Формула объема
Переменные
Прямоугольный Сплошной или кубовидный
В = Д × Ш × В
Д = Длина
Ш = Ширина
В = Высота
24 Куб
V = a 3
a = длина края или стороны
Цилиндр
V = π r 2 7 3 h
4 r = радиус круглого основания
h = высота
Призма
V = B × h
B = площадь основания, (B = сторона 2 или длина. ширина)
ширина)
h 1 9092 5 = высота 1
Сфера
V = (4⁄3)π r 3
r = радиус сферы
⁄3) × Ш × В
B = площадь основания,
h = высота пирамиды
Круговой конус правый
V = (1⁄3)πr 2 h
r = высота 19048 9043 90 90 90 круглого основания 90 3
Квадратный или прямоугольный Пирамида
V = (1⁄3) × длина × ширина × высота
l = длина основания,
w = ширина основания,
h = высота (от основания до кончика)
1
Эллипсоид
V = (4⁄3) × π × a × b × c
a, b, c = полуоси эллипсоида 3 ⁄ (6 √2)
a = Длина края
Решенные примеры
Вопрос 1) Размеры прямоугольного резервуара для воды даны как 2 м 75 см, 1 м 80 см 0 и 1. Сколько литров воды можно налить в бак данных размеров?
Сколько литров воды можно налить в бак данных размеров?
Решение) Как мы знаем, что 1м = 100см.
Размеры резервуара: 2 м 75 см, 1 м 80 см и 1 м 40 см.
Мы можем записать это как 275 см, 180 см, 140 см
Теперь мы знаем, что объем прямоугольного параллелепипеда равен, Объем = l × b × h 3
Поскольку 1000 см = 1 литр
Таким образом, V = 6930 литров
Следовательно, бак может вместить 6930 литров воды.
Недавно обновленные страницы
Диагональ квадратной формулы — значение, вывод и решенные примеры
Формула дисперсионного анализа — определение, полная форма, статистика и примеры
Средняя формула — методы отклонения, решенные примеры и часто задаваемые вопросы
Формула процентной доходности — APY, атомная экономика и решенная Пример
Формула серии – определение, примеры решений и часто задаваемые вопросы
Формула площади поверхности квадратной пирамиды – определение и вопросы
Формула диагонали квадрата – значение, вывод и примеры решения
Формула дисперсионного анализа — определение, полная форма, статистика и примеры
Формула среднего — методы отклонения, примеры решений и часто задаваемые вопросы
Формула процентного выхода — APY, атомная экономика и пример решения
Формула серии — определение, примеры решения и часто задаваемые вопросы
Площадь поверхности квадратной пирамиды Формула — определение и вопросы
Актуальные темы
Что такое объем — Физика | Определение и расчет
Том является базовой физической величиной . Объем является производной величиной и выражает трехмерную протяженность объекта . Объем часто количественно измеряется с использованием производной единицы СИ, кубических метров .
Объем является производной величиной и выражает трехмерную протяженность объекта . Объем часто количественно измеряется с использованием производной единицы СИ, кубических метров .
Например, объем внутри сферы (то есть объем шара) получается из V = 4/3πr 3 , где r — радиус сферы. Другой пример: объем куба равен произведению стороны на сторону. Поскольку все стороны квадрата одинаковы, длина одной из сторон может быть равна 9.0290 в кубе .
Если одна сторона квадрата равна 3 метрам, объем будет равен 3 метрам на 3 метра на 3 метра или 27 кубическим метрам.
Формулы для расчета различных объемов
Формулы объема для некоторых обычных трехмерных объектов:
Что такое удельный объем
Типичные плотности различных веществ при атмосферном давлении.
Удельный объем является интенсивной переменной , тогда как объем является экстенсивной переменной. Стандартная единица измерения удельных объемов в системе СИ — кубический метр на килограмм (м 3 /кг). Стандартной единицей измерения в английской системе является кубический фут на фунт массы (фут 3 /фунт).
Стандартная единица измерения удельных объемов в системе СИ — кубический метр на килограмм (м 3 /кг). Стандартной единицей измерения в английской системе является кубический фут на фунт массы (фут 3 /фунт).
Плотность (ρ) вещества обратно пропорциональна его удельному объему (ν).
ρ = m/V = 1/ρ
Плотность определяется как масса на единицу объема . Это также интенсивное свойство , которое математически определяется как масса, деленная на объем:
ρ = m/V
Материалы с наименьшим удельным объемом — самые плотные материалы на Земле
Поскольку 90 290 нуклонов 90 291 (90 290 протонов 90 291 и 90 290 нейтронов 90 291 ) составляют большую часть массы обычных атомов, плотность обычного вещества, как правило, ограничивается тем, насколько плотно мы можем упаковать эти нуклоны, и зависит от внутренней атомной структуры. вещество. Самый плотный материал , обнаруженный на Земле, — это металлический осмий . Тем не менее, его плотность бледнеет по сравнению с плотностью экзотических астрономических объектов, таких как белые карлики и .0290 нейтронных звезд .
вещество. Самый плотный материал , обнаруженный на Земле, — это металлический осмий . Тем не менее, его плотность бледнеет по сравнению с плотностью экзотических астрономических объектов, таких как белые карлики и .0290 нейтронных звезд .
Список самых плотных материалов:
- Осмий – 22,6 x 10 3 кг/м 3
- Иридий – 22,4 x 10 30 8
- Платина – 21,5 x 10 3 кг/м 3
- Рений – 21,0 x 10 3 кг/м 3
- Плутоний – 19,8 x 10 3 07 90 8 кг/м 3 9087
- Золото – 19,3 x 10 3 кг/м 3
- Вольфрам – 19,3 x 10 3 кг/м 3
- Уран – 18,8 x 10 3 кг/м 3
- Тантал – 18,8 7 кг/м 3
- Ртуть – 13,6 x 10 3 кг/м 3
- Родий – 12,4 x 10 3 кг/м 3
- Торий – 11,7 x 10 м 9 0 8 3
- Свинец – 11,3 x 10 3 кг/м 3
- Серебро – 10,5 x 10 3 кг/м 3
3
Следует отметить, что плутоний является промышленным изотопом и создается из урана в ядерных реакторах. Но ученые обнаружили следовые количества встречающегося в природе плутония.
Но ученые обнаружили следовые количества встречающегося в природе плутония.
Если учитывать промышленные элементы, то самым плотным на данный момент является Hassium . Хассий — это химический элемент с символом Hs и атомным номером 108. Это синтетический элемент (впервые синтезированный в Хассе в Германии) и радиоактивный. Самый стабильный известный изотоп, 269 Hs имеет период полураспада примерно 9,7 секунды. Расчетная плотность составляет 40,7 x 10 3 кг/м 3 . Плотность хассия обусловлена его 90 290 высоким атомным весом 90 291 и значительным уменьшением 90 290 ионных радиусов 90 291 элементов в ряду лантаноидов, известных как 90 290 лантанидное и актинидное сжатие 90 291 .
За плотностью хассия следует мейтнерий (элемент 109, названный в честь физика Лизы Мейтнер), расчетная плотность которого составляет 37,4 x 10 3 кг/м 3 .
Изменения удельного объема
В общем, плотность и, следовательно, удельный объем можно изменить путем изменения давления или температуры . Увеличение давления всегда увеличивает плотность материала. Влияние давления на плотность жидкостей и твердых тел очень мало. С другой стороны, плотность газов сильно зависит от давления. Это выражается сжимаемость . Сжимаемость измеряет относительное изменение объема жидкости или твердого вещества в ответ на изменение давления.
Влияние температуры на плотность жидкостей и твердых тел также очень важно. Большинство веществ расширяются при нагревании и сжимаются при охлаждении . Однако величина расширения или сжатия варьируется в зависимости от материала. Это явление известно как тепловое расширение . Изменение объема материала при изменении температуры определяется следующим соотношением:
Изменение объема материала при изменении температуры определяется следующим соотношением:
где ∆T — изменение температуры, V — исходный объем, ∆V — изменение объема, а α V — коэффициент объемного расширения .
Следует отметить и исключения из этого правила. Например, вода отличается от большинства жидкостей тем, что она становится менее плотной при замерзании . Его максимальная плотность составляет 3,98 °C (1000 кг/м 3 ), тогда как плотность льда составляет 917 кг/м 3 . Он отличается примерно на 9% и поэтому плавает на льду на жидкой воде
Объем атома и ядра
Строение материи.
Атом состоит из небольшого, но массивного ядра , окруженного облаком быстро движущихся электронов . Ядро состоит из протонов и нейтронов . Типичные радиусы ядер имеют порядок 10 −14 м. Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму:
Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму:
г = г 0 . A 1/3
где r 0 = 1,2 x 10 -15 m = 1,2 фм
Если мы используем это приближение, мы, следовательно, ожидаем, что объем ядра будет порядка 4 /3πr 3 или 7,23 × 10 −45 м 3 для ядер водорода или 1721×10 −45 м 3 для 238 ядер U. Это объемы ядер, а в атомных ядрах (протонов и нейтронов) содержится около 99,95% массы атома.
Является ли атом пустым пространством?
Образное изображение атома гелия-4 с электронным облаком в оттенках серого. Протоны и нейтроны, скорее всего, находятся в одном пространстве, в центральной точке. Источник wikipedia.org License CC BY-SA 3.0
Объем атома примерно на на 15 порядков больше чем объем ядра. Для атома урана ван-дер-ваальсов радиус составляет около 186 пм = 1,86 × 10 −10 м . Радиус Ван-дер-Ваальса, r w , атома — это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения для другого атома. Атом урана имеет объем около 26,9 × 10 −30 м 3 , принимая сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает лишь около 1721×10 −45 м 3 место. Эти электроны вместе весят лишь часть (скажем, 0,05%) всего атома.
Радиус Ван-дер-Ваальса, r w , атома — это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения для другого атома. Атом урана имеет объем около 26,9 × 10 −30 м 3 , принимая сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает лишь около 1721×10 −45 м 3 место. Эти электроны вместе весят лишь часть (скажем, 0,05%) всего атома.
Может показаться, что пространство и материя пусты , но это не . Из-за квантовой природы электронов электроны не являются точечными частицами, а размазаны по всему атому. Классическое описание нельзя использовать для описания вещей на атомном уровне. В атомном масштабе физики обнаружили, что квантовая механика очень хорошо описывает вещи в этом масштабе. Расположение частиц в квантовой механике не находится в точном положении, и они описываются функция плотности вероятности . Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как «электронное облако »).
Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как «электронное облако »).
Объем теплоносителя в системе теплоснабжения реактора
Ядерный реактор и система теплоснабжения первого контура ВВЭР-1200.
Источник: gidropress.podolsk.ru
используется с разрешения АО ОКБ «ГИДРОПРЕСС»
В типовых современных водо-водяных реакторах (PWR), система охлаждения реактора (RCS), показанная на рисунке, состоит из:
- корпуса реактора содержит ядерное топливо
- четырех параллельных контуров теплопередачи , соединенных с корпусом реактора.
- каждый контур содержит главный насос охлаждающей жидкости и парогенератор .
- система включает в себя компенсатор давления и его вспомогательные системы
Все компоненты СТР расположены внутри здания защитной оболочки.
Внутри корпуса реактора, контуров и парогенераторов при нормальной работе находится сжатая жидкая вода. Давление поддерживается примерно на уровне 16 МПа . При таком давлении вода кипит примерно при 350°C (662°F). Температура воды на входе составляет около 290°C (554°F). Вода (хладагент) нагревается в активной зоне реактора примерно до 325°C (617°F) по мере прохождения воды через активную зону. Как видно, реактор содержит недогретые теплоносители примерно на 25°C (расстояние от точки насыщения). Это высокое давление поддерживается компенсатором давления, отдельным сосудом, подключенным к первому контуру (горячая ветвь) и частично заполненным водой (частично насыщенным паром), которая нагревается до температура насыщения (точка кипения) для желаемого давления с помощью погружных электрических нагревателей . Температуру в компенсаторе давления можно поддерживать на уровне 350 °C. Около 60% объема компенсатора давления занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар .
Около 60% объема компенсатора давления занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар .
Объемы типичных PWR приведены в следующей таблице.
Это иллюстративный пример, и следующие данные не соответствуют какой-либо конструкции реактора.
Следует отметить, что объем охлаждающей жидкости значительно изменяется в зависимости от температуры охлаждающей жидкости. Общая масса теплоносителя всегда остается неизменной. Изменение объема воды не является изменением запаса воды. Объем теплоносителя реактора изменяется с температурой из-за изменений плотности . Большинство веществ расширяются с при нагревании и сжимаются при охлаждении . Однако величина расширения или сжатия варьируется в зависимости от материала. Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением:
Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением:
, где ∆T — изменение температуры, V — первоначальный объем, ∆V — изменение объема и α V — коэффициент объемного расширения . Плотность жидкой (сжатой) воды как функция температуры воды
Коэффициент объемного теплового расширения для воды непостоянен в диапазоне температур и увеличивается с температурой ( особенно при 300° С ). Поэтому изменение плотности не является линейным в зависимости от температуры (как показано на рисунке).
См. также: Паровые столы.
При нормальных условиях общий объем теплоносителя в системе теплоснабжения реактора почти постоянен. С другой стороны, в условиях переходной нагрузки, объем может значительно измениться . Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Эти эффекты должны контролироваться системой контроля уровня компенсатора давления.
Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Эти эффекты должны контролироваться системой контроля уровня компенсатора давления.
Контрольный объем – Анализ контрольного объема
Контрольный объем – это фиксированная область в пространстве, выбранная для термодинамического исследования баланса массы и энергии для проточных систем. Граница контрольного объема может быть действительной или воображаемой оболочкой . Поверхность управления является границей контрольного объема.
Например, анализ контрольного объема можно использовать для определения скорости изменения количества движения жидкости. В этом анализе будет рассматриваться струйная трубка ( контрольный объем ), как мы делали для уравнения Бернулли. В этом контрольном объеме , любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость внутри объема.
В этом анализе будет рассматриваться струйная трубка ( контрольный объем ), как мы делали для уравнения Бернулли. В этом контрольном объеме , любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость внутри объема.
См. также: Формула импульса.
Как видно из рисунка, метод контрольного объема можно использовать для анализа закона сохранения количества движения в жидкости. Контрольный объем представляет собой воображаемую поверхность , в котором содержится интересующий том. Контрольный объем может быть неподвижным или подвижным, жестким или деформируемым. Для определения всех сил, действующих на поверхности контрольного объема, необходимо решить законы сохранения в этом контрольном объеме.
Выбор контрольного объема
В качестве контрольного объема можно выбрать любой произвольный объем, через который протекает жидкость. Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе.
Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе.
Пример: Струя воды попадает в неподвижную плиту
Неподвижная плита (например, лопасть водяной мельницы) отклоняет поток воды со скоростью 1 м/с и углом 90° . Это происходит при атмосферном давлении, а массовый расход равен Q =1 м 3 /с .
- Рассчитайте силу давления.
- Рассчитайте силу тела.
- Рассчитайте общую силу.
- Рассчитайте результирующую силу.
Решение
- Сила давления равна нулю, так как давление на входе, а выходы в контрольный объем атмосферные.

- Поскольку контрольный объем невелик, мы можем игнорировать силу тела из-за веса гравитации.
- F x = ρ.Q.(w 1x – w 2x ) = 1000 . 1 . (1 – 0) = 1000 Н
F y = 0
F = (1000, 0) - Суммарная сила имеет такое же направление, что и результирующая сила на плоскости Ф (трением и весом пренебрегаем).
h
Струя воды действует на пластину с силой 1000 Н в направлении x.
Каталожные номера:
Реакторная физика и теплогидравлика:
- Дж. Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983).
- Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную технику, 3-е изд.



