Зачастую в рамках решения задач по тригонометрии нам приходится искать множество значений функции на области определения или отрезке. Например, такой поиск нужно делать, если приходится решать разные типы неравенств, при оценке выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми можно вычислить область значения и область определения функции, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графически. Прочитав эту статью, вы получите исчерпывающее представление о том, что такое область значения функции.
Начнем с базовых определений.
Множество значений функции y = f(x) – это множество всех значений на некотором интервале x, которые данная функция принимает при переборе всех значений x∈X.
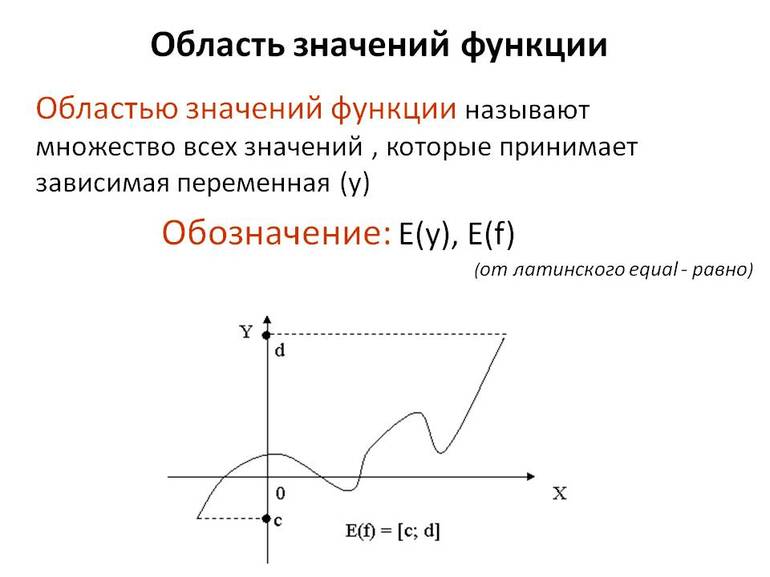
Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).
Область значений некоторой функции обычно принято называть и обозначать E(f).
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.
Ниже приводится иллюстрация, на которой показаны некоторые примеры, как построить графики функций и их построение. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
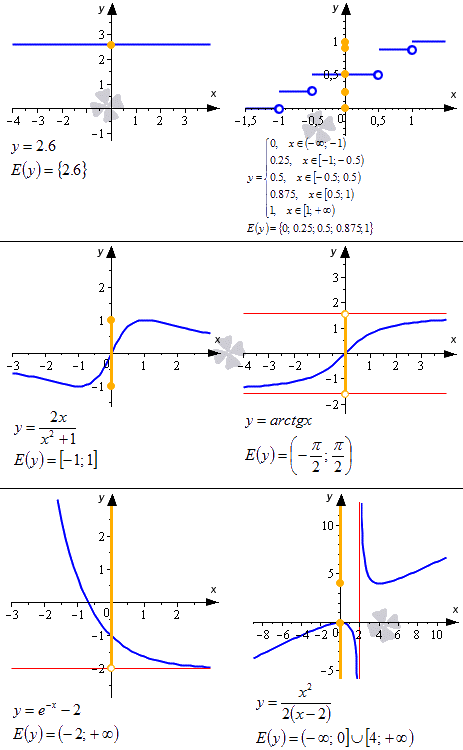
Как найти область значения функции? Очевидно, что область или множество значений функции можно найти или получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.
Рассмотрим основные способы, как определить область значения функции.
Первый этап – определить тип функции. Функция может быть квадратичной, а также содержать дроби и корни.
Начнем с определения множества значений непрерывной функции y = f(x) на некотором отрезке, обозначенном [a; b]. Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего maxx∈a; bf(x) и наименьшего значения minx∈a; bf(x). Значит, у нас получится отрезок minx∈a; bf(x); maxx∈a; bf(x), в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Условие: найдите область значений y = arcsin x.
Решение
В общем случае область определения арксинуса располагается на отрезке [-1; 1]. Нам надо определить наибольшее и наименьшее значение указанной функции на нем.
y’ = arcsin x’=11-x2
Мы знаем, что производная функции будет положительной для всех значений x, расположенных в интервале [-1; 1], то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x, равном -1, а самое большое – при x, равном 1.
minx∈-1; 1arcsin x=arcsin-1=-π2maxx∈-1; 1arcsin x=arcsin 1=π2
Таким образом, область значений функции арксинус будет равна E(arcsin x)=-π2; π2.
Ответ: E(arcsin x)=-π2; π2
Условие: вычислите область значений y=x4-5×3+6×2 на заданном отрезке [1; 4].
Решение
Как найти значение функции? Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
y’=x4-5×3+6×2’=4×3+15×2+12x=x4x2-15x+12y’=0⇔x(4×2-15x+12)=0x1=0∉1; 4 или 4×2-15x+12=0D=-152-4·4·12=33×2=15-338≈1.16∈1; 4; x3=15+338≈2.59∈1; 4
Теперь найдем значения заданной функции в концах отрезка и точках x2=15-338; x3=15+338:
y(1)=14-5·13+6·12=2y15-338=15-3384-5·15-3383+6·15-3382==117+16533512≈2.08y15+338=15+3384-5·15+3383+6·15+3382==117-16533512≈-1.62y(4)=44-5·43+6·42=32
Как найти множество значений функции? Значит, множество значений функции будет определяться отрезком 117-16533512; 32.
Ответ: 117-16533512; 32.
Перейдем к нахождению множества значений непрерывной функции y = f(x) в промежутках (a; b), причем a; +∞, -∞; b, -∞; +∞.
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведение функции в заданных условиях. Для этого у нас есть все необходимые данные.
Условие: вычислите область значений функции y=1×2-4 на интервале (-2; 2).
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
y’=1×2-4’=-2x(x2-4)2y’=0⇔-2x(x2-4)2=0⇔x=0∈(-2; 2)
У нас получилось максимальное значение, равное 0, поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:
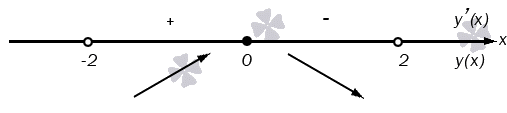
То есть, y(0)=102-4=-14 будет максимальным значением функции.
Теперь определим поведение функции при таком x, который стремится к -2 с правой стороны и к +2 с левой стороны. Иными словами, найдем односторонние пределы:
limx→-2+01×2-4=limx→-2+01(x-2)(x+2)==1-2+0-2-2+0+2=-14·1+0=-∞limx→2+01×2-4=limx→2+01(x-2)(x+2)==12-0-22-0+2=14·1-0=-∞
У нас получилось, что значения функции будут возрастать от минус бесконечности до -14 тогда, когда аргумент изменяется в пределах от -2 до 0. А когда аргумент меняется от 0 до 2, значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (-∞; -14].
Ответ: (-∞; -14].
Условие: укажите множество значений y=tg x на заданном интервале -π2; π2.
Решение
Нам известно, что в общем случае производная тангенса в -π2; π2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:
limx→π2+0tg x=tg-π2+0=-∞limx→π2-0tg x=tgπ2-0=+∞
Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от -π2 до π2,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.
Ответ: -∞; +∞.
Условие: определите, какова область значений функции натурального логарифма y = ln x.
Решение
Нам известно, что данная функция является определенной при положительных значениях аргумента D(y)=0; +∞. Производная на заданном интервале будет положительной: y’=ln x’=1x. Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:
limx→0+0ln x=ln(0+0)=-∞limx→∞ln x=ln+∞=+∞
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Условие: определите, какова область значений функции y=9×2+1.
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
y’=9×2+1’=-18x(x2+1)2y’=0⇔x=0y’≤0⇔x≥0y’≥0⇔x≤0
В итоге мы определили, что данная функция будет убывать, если x≥0; возрастать, если x≤0; она имеет точку максимума y(0)=902+1=9 при переменной, равной 0.
Посмотрим, как же ведет себя функция на бесконечности:
limx→-∞9×2+1=9-∞2+1=9·1+∞=+0limx→+∞9×2+1=9+∞2+1=9·1+∞=+0
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9. Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0. Мы отобразили это на рисунке:
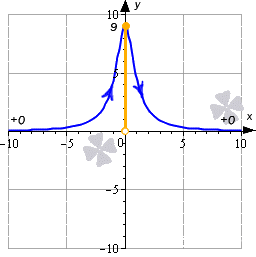
На нем видно, что областью значений функции будет интервал E(y)=(0; 9]
Ответ: E(y)=(0; 9]
Если нам надо определить множество значений функции y = f(x) на промежутках [a; b), (a; b], [a; +∞), (-∞; b], то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Условие: определите, какой будет область значений y=xx-2.
Решение
Поскольку знаменатель функции не должен быть обращен в 0, то D(y)=-∞; 2∪2; +∞.
Начнем с определения множества значений функции на первом отрезке -∞; 2, который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.
limx→2-0xx-2=2-02-0-2=2-0=-∞limx→-∞xx-2=limx→-∞x-2+2x-2=limx→-∞1+2x-2=1+2-∞-2=1-0
Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1. Если же значения x меняются от минус бесконечности до 2, то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала -∞; 1. Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.
Для открытого луча 2; +∞ производим точно такие же действия. Функция на нем также является убывающей:
limx→2+0xx-2=2+02+0-2=2+0=+∞limx→+∞xx-2=limx→+∞x-2+2x-2=limx→+∞1+2x-2=1+2+∞-2=1+0
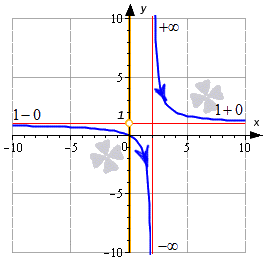
Значения функции на данном отрезке определяются множеством 1; +∞. Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств -∞; 1 и 1; +∞.
Ответ: E(y)=-∞; 1∪1; +∞.
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Условие: определите область значений синуса y = sin x.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0; 2π и смотрим, каким будет множество значений на нем.
y’=(sin x)’=cos xy’=0⇔cos x=0⇔x=π2+πk, k∈Z
В рамках 0; 2π у функции будут точки экстремума π2 и x=3π2. Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.
y(0)=sin 0=0yπ2=sin π2=1y3π2=sin3π2=-1y(2π)=sin(2π)=0⇔minx∈0; 2πsin x=sin3π2=-1, maxx∈0; 2πsin x=sinπ2=1
Ответ: E(sin x)=-1; 1.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения (или указать). Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Условие: определите область значения y=3arccosx3+5π7-4.
Решение
Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E(arccos x)=0; π или 0≤arccos x≤π. Мы можем получить функцию arccosx3+5π7 из арккосинуса, сдвинув и растянув ее вдоль оси Ox, но такие преобразования нам ничего не дадут. Значит, 0≤arccosx3+5π7≤π.
Функция 3arccosx3+5π7 может быть получена из арккосинуса arccosx3+5π7 с помощью растяжения вдоль оси ординат, т.е. 0≤3arccosx3+5π7≤3π. Финалом преобразований является сдвиг вдоль оси Oy на 4 значения. В итоге получаем двойное неравенство:
0-4≤3arccosx3+5π7-4≤3π-4⇔-4≤3arccosx3+5π7-4≤3π-4
Мы получили, что нужная нам область значений будет равна E(y)=-4; 3π-4.
Ответ: E(y)=-4; 3π-4.
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Условие: вычислите, какова будет область значений функции y=22x-1+3.
Решение
Перепишем функцию, заданную в условии, как y=2·(2x-1)-12+3. Для степенной функции y=x-12 область значений будет определена на промежутке 0; +∞, т.е. x-12>0. В таком случае:
2x-1-12>0⇒2·(2x-1)-12>0⇒2·(2x-1)-12+3>3
Значит, E(y)=3; +∞.
Ответ: E(y)=3; +∞.
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
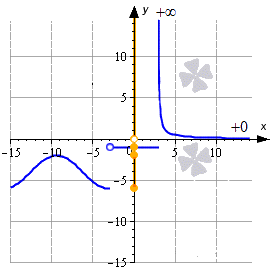
Условие: дана функция y=2sinx2-4, x≤-3-1, -3<x≤31x-3, x>3. Вычислите область ее значений.
Решение
Данная функция является определенной для всех значений x. Проведем ее анализ на непрерывность при значениях аргумента, равных -3 и 3:
limx→-3-0f(x)=limx→-32sinx2-4=2sin-32-4=-2sin32-4limx→-3+0f(x)=limx→-3(1)=-1⇒limx→-3-0f(x)≠limx→-3+0f(x)
Имеем неустранимый разрыв первого рода при значении аргумента -3. При приближении к нему значения функции стремятся к -2sin32-4, а при стремлении x к -3 с правой стороны значения будут стремиться к -1.
limx→3-0f(x)=limx→3-0(-1)=1limx→3+0f(x)=limx→3+01x-3=+∞
Имеем неустранимый разрыв второго рода в точке 3. Когда функция стремится к нему, ее значения приближаются к -1, при стремлении к той же точке справа – к минус бесконечности.
Значит, вся область определения данной функции является разбитой на 3 интервала (-∞; -3], (-3; 3], (3; +∞).
На первом из них у нас получилась функция y=2sinx2-4. Поскольку -1≤sin x≤1, получаем:
-1≤sinx2<1⇒-2≤2sinx2≤2⇒-6≤2sinx2-4≤-2
Значит, на данном промежутке (-∞; -3] множество значении функции – [-6;2].
На полуинтервале (-3; 3] получилась постоянная функция y =-1. Следовательно, все множество ее значений в данном случае будет сводится к одному числу -1.
На втором промежутке 3; +∞ у нас есть функция y=1x-3. Она является убывающей, потому что y’=-1(x-3)2<0. Она будет убывать от плюс бесконечности до 0, но самого 0 не достигнет, потому что:
limx→3+01x-3=13+0-3=1+0=+∞limx→+∞1x-3=1+∞-3=1+∞+0
Значит, множество значений исходной функции при x > 3 представляет собой множество 0; +∞. Теперь объединим полученные результаты: E(y)=-6; -2∪-1∪0; +∞.
Ответ: E(y)=-6; -2∪-1∪0; +∞.
Решение показано на графике:
Условие: есть функция y=x2-3ex. Определите множество ее значений.
Решение
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
y’=x2-3ex’=2xex-ex(x2-3)e2x=-x2+2x+3ex=-(x+1)(x-3)ex
Мы знаем, что производная обратится в 0, если x=-1 и x=3. Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.
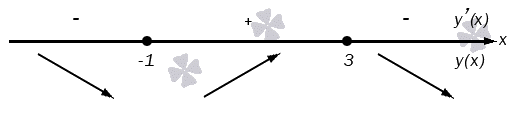
Функция будет убывать на (-∞; -1]∪[3; +∞) и возрастать на [-1; 3]. Точкой минимума будет -1, максимума –3.
Теперь найдем соответствующие значения функции:
y(-1)=-12-3e-1=-2ey(3)=32-3e3=6e-3
Посмотрим на поведение функции на бесконечности:
limx→-∞x2-3ex=-∞2-3e-∞=+∞+0=+∞limx→+∞x2-3ex=+∞2-3e+∞=+∞+∞==limx→+∞x2-3’ex’=limx→+∞2xex=+∞+∞==limx→+∞2x'(ex)’=2limx→+∞1ex=2·1+∞=+0
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
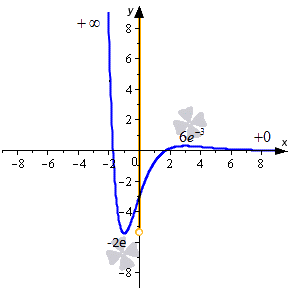
На нем видно, что значения функции будут убывать от плюс бесконечности до -2e тогда, когда аргумент меняется от минус бесконечности до -1. Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6e-3 до 0, но при этом 0 достигнут не будет.
Таким образом, E(y)=[-2e; +∞).
Ответ: E(y)=[-2e; +∞)
Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
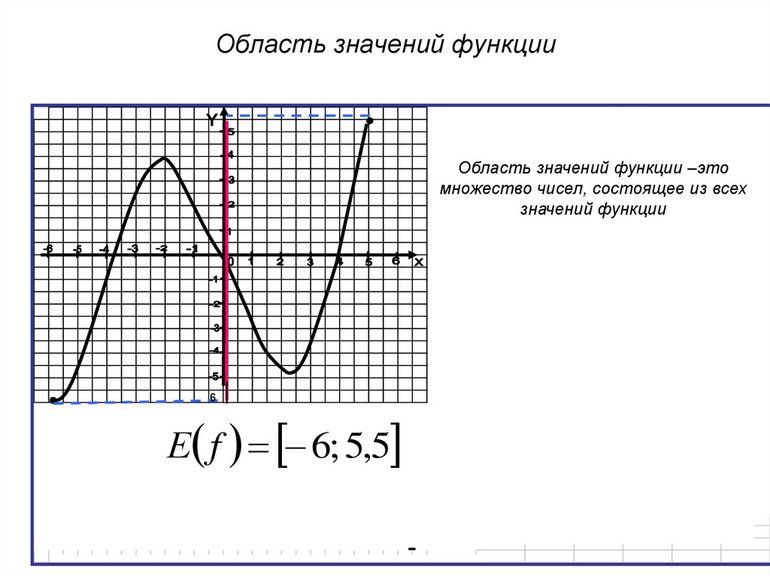
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Например, нужно найти область значений квадратичной функции y = 3x 2 — 2x — 1. Следует записать уравнение 3x 2 — 2x — 1 = 0. Ордината вычисляется таким образом: y0 = -D / 4a = -[b 2 — 4ac] / 4a = -[(-2)^2 — 4 * 3 * (-1)] / (4 * 3) = -16 / 12 = -4/3. Если коэффициент а>0, то ветви параболы направлены вверх. Следовательно, E (y) = (-4/3;+бесконечность).
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

- (-бесконечность;+бесконечность): y =kx + b, y = x^(2n+1), y = x^(1/(2n+1)), y = log (x) с основанием а, y = tg (x) и y = ctg (x).
- [0;+бесконечность): y = x^(2n), y = x^(1/(2n)) и y = a^x.
- (-бесконечность;0] U [0;+бесконечность) только для y = k / x (гипербола).
- [-1;1]: y = sin (x) и y = cos (x).
- [0;Pi]: y = arccos (x) и arcsin (x).
- [-Pi/2;Pi/2]: y = arctg (x) и arcsin (x).
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
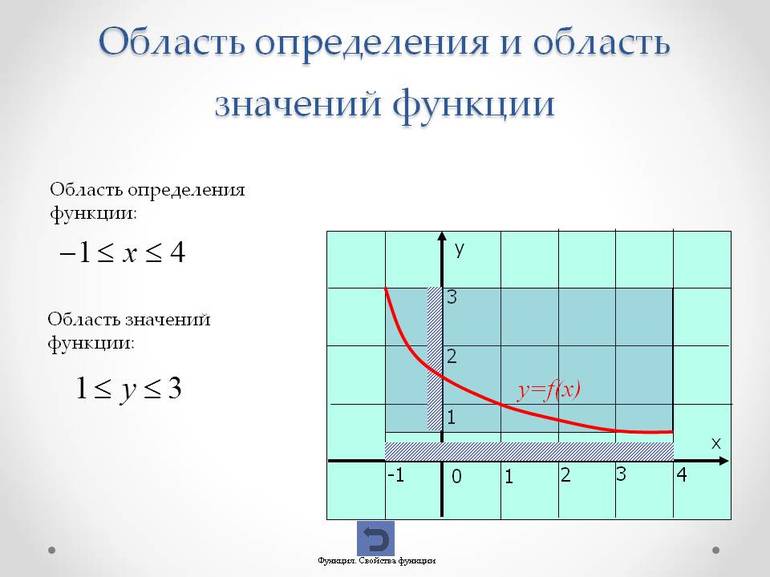
- В случае, когда функция f (x) является непрерывной, и наблюдается ее возрастание или убывание на отрезке [a;b], то множество значений — интервал [f (a);f (b)].
- Если y = f (x) обладает непрерывностью на промежутке [a;b], и существует некоторое минимальное m и максимальное М ее значения, то множеством ее значений является интервал [m;M].
- При непрерывности и дифференцируемости функции на промежутке [a;b], она имеет минимальное и максимальное значения на данном промежутке.
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
- Отдельное нахождение значений элементов сложной функции.
- Оценочный.
- Учет непрерывности и монотонности.
- Взятие производной.
- Использование max и min функции.
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
- Выполнить необходимые преобразования — упростить выражение.
- Разбить выражение на элементы.
- Выполнить поиск E (f) для каждого элемента.
- Произвести замену.
- Анализ.
- Результат решения.
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
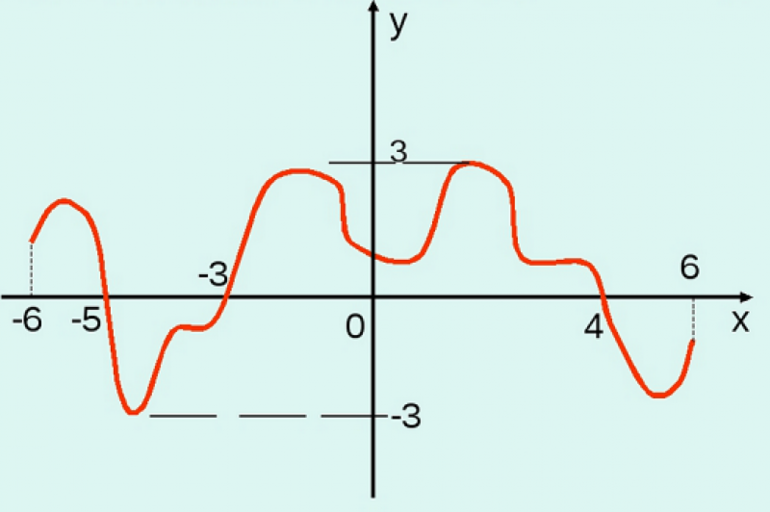
- Упростить (выделить квадрат): y = log0.5 (4 — 2 * 3^x — 9^x) = log0.5 [5 — (1 — 2 * 3^x — 9^x)] = log0.5 [5 — (3^x + 1)].
- Разбить на элементарные функции: y = 3^x, y = 3^x + 1, y = [-(3^x + 1)]^2 и y = [5 — (3^x + 1)]^2.
- Определить для каждого элемента E (f): E (3^x) = (0;+бесконечность), E (3^x + 1) = (1;+бесконечность), E ([-(3^x + 1)]^2) = (-бесконечность;-1) и E ([5 — (3^x + 1)]^2) = (-бесконечность;4).
- Произвести замену: t = 5 — (3^x + 1)]^2 (-бесконечность <= t <=4).
- Анализ: поскольку E (f) на луче (-бесконечность;4) совпадает с интервалом (0;4), то функция непрерывна и убывает. Необходимо отметить, что интервал (0;4) получен при пересечении луча (-бесконечность;4) с областью определения функции логарифмического типа (0;+бесконечность). На интервале (0;4) эта функция непрерывна и убывает. Если t>0, то она стремится к бесконечности. Когда t = 4, ее значение равно -2.
- Результат решения — искомый интервал: E (f) = (-2;+бесконечность).
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
- Доказать непрерывность.
- Составить неравенство или неравенства для нескольких функций.
- Узнать оценку.
- Записать интервал.
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
- Функция вида y = cos (x) является непрерывной.
- Неравенства: -1<=cos (7x)?1 и -5<=5 * cos (x)?5.
- Оценка получает при объединении неравенств: -6<=y?6. При значениях независимой переменной x = Pi и x = 0 функция принимает значения -6 и 6 соответственно (нижняя и верхняя границы). Функция состоит из двух элементов, следовательно, она является линейной и непрерывной.
- Интервал: E (y) = [-6;6].
Метод позволяет найти решение без использования дополнительных вычислений. Но при его использовании легко ошибиться.
Учет непрерывности и монотонности
Одним из простых способов решения, который специалисты рекомендуют новичкам, является метод учета непрерывности и монотонности. Для этого существует специальный алгоритм:
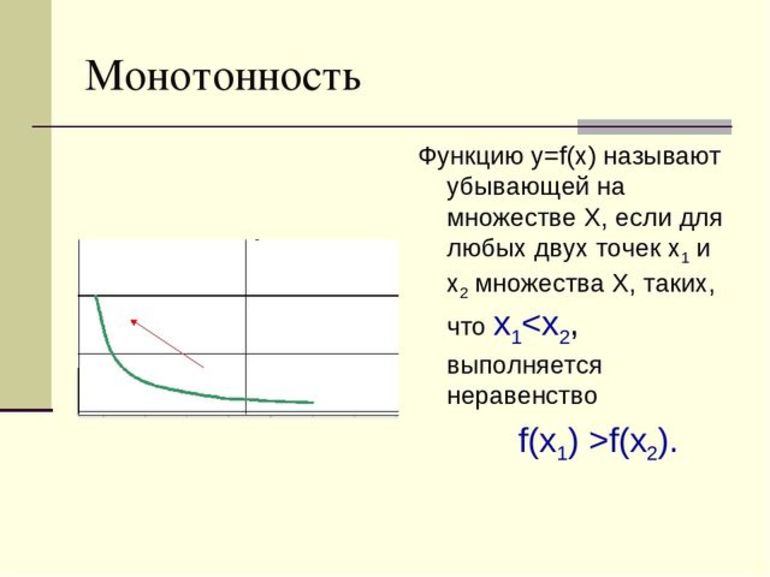
- Упростить выражение.
- Выполнить замену при необходимости.
- Найти вершину графика.
- Определить промежуток.
- Вычислить максимальное и минимальное значения.
- Записать E (f).
Например, существует некоторая функция y = cos (2x) + 2cos (x). Необходимо найти ее E. Искать следует по алгоритму решения методом учета монотонности и непрерывности:
- Упростить (по формуле двойного угла): y = 2 * (cos (x))^2 + 2cosx — 1.
- Замена t = cos (x): y = 2 * t 2 + 2 * t — 1 = 2 * (t + 0,5)^2 — 1,5.
- Показательная функция является параболой. Она монотонна, непрерывна и имеет вершину по оси ОУ -1,5. Промежуток, который рассматривается — [-1;1], поскольку E (cos (x)) = [-1;1].
- Минимальное значение равно -1,5, так как ветви направлены вверх. Максимальное на промежутке [-1;1] – MAX (y) = 3. Для его нахождения нужно построить график параболы y = 2 * (t + 0,5)^2 — 1,5.
- Искомый интервал — E (cos (2x) + 2cos (x)) = [-1,5;3].
Чтобы построить график параболы, нужно найти ее вершину и точки пересечения с осью абсцисс. Последние находятся при решении уравнения 2 * (t + 0,5)^2 — 1,5 = 0. Однако существует способ намного проще. Для этого следует привести выражение к виду 2 * (t + 0,5)^2 = 1,5. Отсюда t = – 0,5. Следовательно, координаты вершины — (-0,5;-1,5). Корни уравнения при его решении: t1 = -[(1 + (3)^0.5)] / 2 и t2 = -[(1 — (3)^0.5)] / 2.
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
- Найти производную.
- Анализ.
- Указать MAX (f) и MIN (f).
- Запись интервала в формате (MIN (f);MAX (f)).
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
- Производная: y’ = [arcsin (x)]’ = 1 / [(1 — x 2 )^0.5].
- Функция возрастает на интервале (-1;1).
- Минимум и максимум на отрезке (-1;1): MIN (arcsin (-1)) = -Pi/2 MAX (arcsin (1)) = Pi/2.
- Интервал: E (arcsin (x)) = [-Pi/2;Pi/2].
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
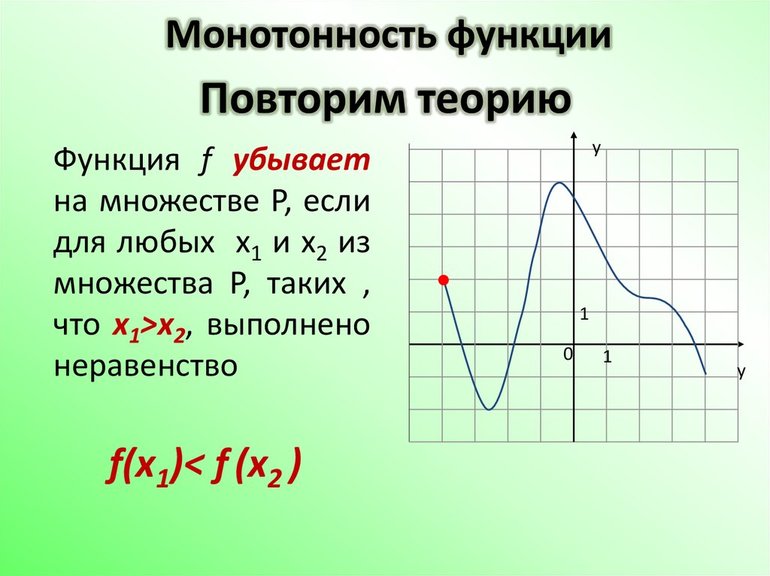
- Производная: y’ = [sin (x)]’ = cos (x).
- Период функции равен 2Pi. Следует взять отрезок [0;2Pi]. Для нахождения множества значений на нем нужно приравнять производную функции к 0, т. е. cos (x) = 0. Найти х = Pi/2 + Pi * к, где «к» принадлежит Z. Точки экстремума равны Pi/2 и 3Pi/2.
- Минимум и максимум на отрезке [0;2Pi): MIN ([sin (3Pi/2)]) = -1 и MAX ([sin (3Pi/2)]) = 1.
- E (sin (x)) = [-1;1].
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.
Загрузить PDF
Загрузить PDF
В каждой функции есть две переменные – независимая переменная и зависимая переменная, значения которой зависят от значений независимой переменной. Например, в функции y = f(x) = 2x + y независимой переменной является «х», а зависимой – «у» (другими словами, «у» – это функция от «х»). Допустимые значения независимой переменной «х» называются областью определения функции, а допустимые значения зависимой переменной «у» называются областью значений функции.[1]
-

1
Определите тип данной вам функции. Областью значений функции являются все допустимые значения «х» (откладываются по горизонтальной оси), которым соответствуют допустимые значения «у». Функция может быть квадратичной или содержать дроби или корни. Для нахождения области определения функции сначала необходимо определить тип функции.
- Квадратичная функция имеет вид: ax2 + bx + c:[2]
f(x) = 2x2 + 3x + 4 - Функция, содержащая дробь: f(x) = (1/x), f(x) = (x + 1)/(x – 1) (и так далее).
- Функция, содержащая корень: f(x) = √x, f(x) = √(x2 + 1), f(x) = √-x (и так далее).
- Квадратичная функция имеет вид: ax2 + bx + c:[2]
-

2
Выберите соответствующую запись для области определения функции. Область определения записывается в квадратных и/или круглых скобках. Квадратная скобка применяется в том случае, когда значение входит в область определения функции; если значение не входит в область определения, используется круглая скобка. Если у функции несколько несмежных областей определения, между ними ставится символ «U».[3]
- Например, область определения [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
-

3
Постройте график квадратичной функции. График такой функции представляет собой параболу, ветви которой направлены либо вверх, либо вниз. Так как парабола возрастает или убывает на всей оси Х, то областью определения квадратичной функции являются все действительные числа. Другими словами, областью определения такой функции является множество R (R обозначает все действительные числа).[4]
- Для лучшего уяснения понятия функции выберите любое значение «х», подставьте его в функцию и найдите значение «у». Пара значений «х» и «у» представляют собой точку с координатами (х,у), которая лежит на графике функции.
- Нанесите эту точку на плоскость координат и проделайте описанный процесс с другим значением «х».
- Нанеся на плоскость координат несколько точек, вы получите общее представление о форме графика функции.
-

4
Если функция содержит дробь, приравняйте ее знаменатель к нулю. Помните, что делить на нуль нельзя. Поэтому, приравняв знаменатель к нулю, вы найдете значения «х», которые не входят в область определения функции.[5]
- Например, найдите область определения функции f(x) = (x + 1)/(x – 1).
- Здесь знаменатель: (х – 1).
- Приравняйте знаменатель к нулю и найдите «х»: х – 1 = 0; х = 1.
- Запишите область определения функции. Область определения не включает 1, то есть включает все действительные числа за исключением 1. Таким образом, область определения функции: (-∞,1) U (1,∞).
- Запись (-∞,1) U (1,∞) читается так: множество всех действительных чисел за исключением 1. Символ бесконечности ∞ означает все действительные числа. В нашем примере все действительные числа, которые больше 1 и меньше 1, включены в область определения.
-

5
Если функция содержит квадратный корень, то подкоренное выражение должно быть больше или равно нулю. Помните, что квадратный корень из отрицательных чисел не извлекается. Поэтому любое значение «х», при котором подкоренное выражение становится отрицательным, нужно исключить из области определения функции.[6]
- Например, найдите область определения функции f(x) = √(x + 3).
- Подкоренное выражение: (х + 3).
- Подкоренное выражение должно быть больше или равно нулю: (х + 3) ≥ 0.
- Найдите «х»: х ≥ -3.
- Область определения этой функции включает множество всех действительных чисел, которые больше или равны -3. Таким образом, область определения: [-3,∞).
Реклама
-

1
Убедитесь, что вам дана квадратичная функция. Квадратичная функция имеет вид: ax2 + bx + c: f(x) = 2x2 + 3x + 4. График такой функции представляет собой параболу, ветви которой направлены либо вверх, либо вниз. Существуют различные методы нахождения области значений квадратичной функции.[7]
- Самый простой способ найти область значений функции, содержащей корень или дробь, – это построить график такой функции при помощи графического калькулятора.
-

2
Найдите координату «х» вершины графика функции. В случае квадратичной функции найдите координату «х» вершины параболы. Помните, что квадратичная функция имеет вид: ax2 + bx + c. Для вычисления координаты «х» воспользуйтесь следующим уравнением: х = -b/2a. Это уравнение является производной от основной квадратичной функции и описывает касательную, угловой коэффициент которой равен нулю (касательная к вершине параболы параллельна оси Х).[8]
- Например, найдите область значений функции 3x2 + 6x -2.
- Вычислите координату «х» вершины параболы: х = -b/2a = -6/(2*3) = -1
-

3
Найдите координату «у» вершины графика функции. Для этого в функцию подставьте найденную координату «х». Искомая координата «у» представляет собой предельное значение области значений функции.
- Вычислите координату «у»: y = 3x2 + 6x – 2 = 3(-1)2 + 6(-1) -2 = -5
- Координаты вершины параболы этой функции: (-1,-5).
-

4
Определите направление параболы, подставив в функцию по крайней мере одно значение «х». Выберите любое другое значение «х» и подставьте его в функцию, чтобы вычислить соответствующее значение «у». Если найденное значение «у» больше координаты «у» вершины параболы, то парабола направлена вверх. Если же найденное значение «у» меньше координаты «у» вершины параболы, то парабола направлена вниз.
- Подставьте в функцию х = -2: y = 3x2 + 6x – 2 = y = 3(-2)2 + 6(-2) – 2 = 12 -12 -2 = -2.
- Координаты точки, лежащей на параболе: (-2,-2).
- Найденные координаты свидетельствуют о том, что ветки параболы направлены вверх. Таким образом, область значений функции включает все значения «у», которые больше или равны -5.
- Область значений этой функции: [-5, ∞)
-

5
Область значений функции записывается аналогично области определения функции. Квадратная скобка применяется в том случае, когда значение входит в область значений функции; если значение не входит в область значений, используется круглая скобка. Если у функции несколько несмежных областей значений, между ними ставится символ «U».[9]
- Например, область значений [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
Реклама
-

1
Постройте график функции. Во многих случаях проще найти область значений функции, построив ее график. Областью значений многих функций с корнями является (-∞,0] или [0,+∞), так как вершина параболы, направленной вправо или влево, лежит на оси Х. В этом случае область значений включает все положительные значения «у», если парабола возрастает, или все отрицательные значения «у», если парабола убывает. Функции с дробями имеют асимптоты, которые определяют область значений.[10]
- Вершины графиков некоторых функций с корнями лежат выше или ниже оси Х. В этом случае область значений определяется координатой «у» вершины параболы. Если, например, координата «у» вершины параболы равна -4 (у = -4), а парабола возрастает, то область значений равна [-4,+∞).
- Самый простой способ построить график функции – это воспользоваться графическим калькулятором или специальным программным обеспечением.
- Если у вас нет графического калькулятора, постройте приблизительный график, подставив в функцию несколько значений «х» и вычислив соответствующие значения «у». Нанесите найденные точки на координатную плоскость, чтобы получить общее представление о форме графика.
-

2
Найдите минимум функции. Построив график функции, вы увидите на нем точку, в которой функция имеет минимальное значение. Если наглядного минимума нет, то он не существует, а график функции уходит в -∞.
- Область значений функции включает все значения «у» за исключением значений асимптот. Зачастую, области значений таких функций записываются так: (-∞, 6) U (6, ∞).
-

3
Определите максимум функции. Построив график функции, вы увидите на нем точку, в которой функция имеет максимальное значение. Если наглядного максимума нет, то он не существует, а график функции уходит в +∞.
-

4
Область значений функции записывается аналогично области определения функции. Квадратная скобка применяется в том случае, когда значение входит в область значений функции; если значение не входит в область значений, используется круглая скобка. Если у функции несколько несмежных областей значений, между ними ставится символ «U».[11]
- Например, область значений [-2,10) U (10,2] включает значения -2 и 2, но не включает значение 10.
- С символом бесконечности ∞ всегда используются круглые скобки.
Реклама
Об этой статье
Эту страницу просматривали 351 484 раза.
Была ли эта статья полезной?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 сентября 2021 года; проверки требуют 5 правок.
Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция[1][2][3].
Определение[править | править код]
Пусть на множестве 










.
Способы нахождения областей значений некоторых функций[править | править код]
- последовательное нахождение значений сложных аргументов функции;
- метод оценок;
- использование свойств непрерывности и монотонности функции;
- использование производной;
- использование наибольшего и наименьшего значений функции;
- графический метод;
- метод введения параметра;
- метод обратной функции.
Терминология[править | править код]
В некоторых источниках различаются понятия области значений и множества значений функции. При этом областью значений функции называется её кодомен, то есть множество 



Множество значений 


Иногда множество значений функции называют областью изменения функции[3].
См. также[править | править код]
- Область определения функции
Примечания[править | править код]
- ↑ У. Рудин. Основы математического анализа.. — М.: Мир, 1976. — С. 32. — 318 с.
- ↑ В. А. Зорич. Математический анализ. Часть I.. — М.: МЦНМО, 2002. — С. 14. — 664 с. — ISBN 5-94057-056-9.
- ↑ 1 2 В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Математический анализ. — М.: МГУ, 1985. — С. 66, 106, 450. — 720 с.
- ↑ Г. Е. Шилов. Математический анализ. Функции одного переменного. Части 1 — 2. — М.: Наука, 1969. — С. 65—69. — 528 с.
Литература[править | править код]
- Функция. Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
- Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
- И. А. Лавров, Л. Л. Максимова. Часть I. Теория множеств // Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд.. — М.: Физматлит, 1995. — С. 13 — 21. — 256 с. — ISBN 5-02-014844-X.
- А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
- Дж. Л. Келли. Глава 0. Предварительные сведения // Общая топология. — 2-е изд.. — М.: Наука, 1981. — С. 19 — 27. — 423 с.
- В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ, часть I. — М.: Наука, 1981. — С. 23 — 36. — 544 с.
- А. Н. Колмогоров. Что такое функция // «Квант» : науч.-поп. физ.-мат. журн. — М.: «Наука», 1970. — № 1. — С. 27-36. — ISSN 0130-2221.
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Функцией, заданной на множестве $X$ и принимающей значения из множества $Y$ называют некую закономерность, по которой каждому элементу из множества $X$ соответствует лишь один и только один элемент из множества $Y$.
Из этого определения следует, что множество (область) значений функции — это те значения функции $y(x)$, которые она может принимать соответственно области её определения. Теперь перейдём к следующему определению.
Определение 2
Область (множество) значений функции на некотором рассматриваемом отрезке — это интервал значений, которые функция принимает на этом рассматриваемом отрезке.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Чаще всего в учебной литературе встречается термин «множество значений функции». Кратко его обозначают $E(f)$.
Как определить область значения функции
Для определения множества значений функции пользуются графическим методом, методом поисков минимума и максимума, вычислением производной и другими.
Определение множества значений функции графическим методом
Графический метод подразумевает построение графика функции и изучение этого графика. Этот метод наиболее удобен, если не известна какая-либо закономерность изменения функции $f(x)$, а есть только набор произвольных точек или собственно сам график.
Пример 1
Рисунок 1. Определение множества значений функции графическим методом
На данном рисунке область значений функции $y=f(x)$ равна $E(y)=3$, так как на протяжении всего отрезка функция $y$ не меняет своего значения и всегда равна $3$, тогда как область определения функции $D(y)=[0;3.5]$.
Скобки в данном случае для области определения функции необходимо использовать квадратные, так как обе точки закрашены, то есть включены в отрезок. В случае если точки не закрашены, они не включаются в отрезок и тогда применяются круглые скобки.
«Множество значений функции» 👇
Метод нахождения области значения функции через производную
Метод нахождения области значения функции через производную состоит в том, чтобы сначала оценить область её определения (то есть определить те значения, которые может принимать аргумент $x$, а затем осуществить процедуру нахождения самой производной. После этого осуществляют поиск значений $x$, при которых производная функции равна нулю и при которых производная не существует.
Рассмотрим пример нахождения области значений функции через производную.
Пример 2
Дана функция $f(x)=sqrt{16-x^2}$. Найдите область её значений.
Сначала определяем, какие значения может принимать $x$ для существования функции.
При значении $x^2>16$ под корнем получается отрицательное число, а это значит, что область определения функции от $[-4;4]$ включительно.
Теперь найдём производную функции:
$(sqrt{16-x^2})’=-frac{x}{sqrt{16-x^2}}$
Если в знаменателе производной нуль, то производной не существует, в данном случае это условие выполняется при $x=±4$.
Приравниваем производную к нулю и находим значения $x$. Производная данной функции принимает нулевое значение при $x=0$. Теперь подставляем найденные значения производной в нашу функцию, и получаем, что наименьшее значение функции — это $f(4)$ и $f(-4)$, при этих значениях функция равна нулю, а наибольшее значение $f(x)$ — при $x=0$, в этой точке функция равна $16$.
Метод поиска минимума и максимума
Метод поиска минимума и максимума основан на том, чтобы найти максимальное и и минимальное значение, которые функция принимает на изучаемой области.
Пример 3
Определите область значений функции:
$y=6-4sinx$
Проанализируем данную функцию. Так как минимальное значение синуса равно минус единице, а а максимальное — единице, то подставив эти значения получаем, что $max(f(x))=10$ при $x=frac{3π}{2}$, а минимум $min(f(x))=2$ при $x=frac{π}{2}$. Следовательно, множество значений, которые может принимать данная функция — $E(x)=[2;10]$.
Разница между областью значения и областью определения функции
Стоит обратить внимание, что область значений функции — не одно и то же с термином «область определения функции».
Определение 3
Область определения функции $D(y)$ — это диапазон таких значений переменной $x$, при которых существует функция $y(x)$.
Например, рассмотрим функцию $y(x)=x^2$. В данном случае область определения этой функции будет множеством вещественных (действительных) чисел $mathbb{R}$, а сама функция будет принимать значения только положительных действительных чисел $mathbb{R}^+$, так как вещественное число, возведённое в квадрат, не может давать отрицательное значение. То есть, в этом примере множество значений функции — это множество положительных вещественных чисел $mathbb{R}^+$.
Также имеют место случаи, когда область определения функции совпадает с областью значений.
В качестве иллюстрации можно рассмотреть функцию $y(x)=2x$. За аргумент $x$ данная функция может принимать любое действительное число из множества $mathbb{R}$, а значения, которые будет принимать сама функция — это удвоенные числа из множества всех действительных чисел. То есть, в данном случае областью значений $E(y)$ будет также всё множество вещественных чисел $mathbb{R}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме


