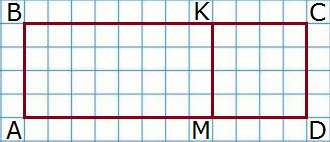
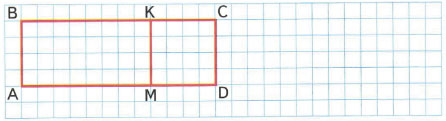
Как можно найти площадь прямоугольника abcd

• 02
  

  Янв 18

• 

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

• S — искомая площадь прямоугольника;
• a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

• S — искомая площадь прямоугольника;
• a — известная сторона;
• P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• d — любая диагональ прямоугольника;
• α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

• S — искомая площадь прямоугольника;
• R — радиус описанной окружности;
• α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

• ТЕСТ:​ ​​Умеете ли вы считать в уме?
• Как легко и быстро считать проценты в уме
• Как найти площадь любого треугольника
• ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
• Как освоить устный счёт школьникам и взрослым

Математика

5 класс

Урок №30

Площадь прямоугольника. Единицы площади

Перечень рассматриваемых вопросов:

– понятие площади фигуры;

-единицы измерения площади; 

– площадь прямоугольника, квадрата; 

– приближенное измерение площади фигуры на клетчатой бумаге.

Тезаурус

Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). 

Квадрат – прямоугольник, у которого все стороны равны. 

Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Основная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?

Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.

Для начала введём понятие площади фигуры.

Если какую-нибудь площадь можно разбить на n квадратов со стороной, например, 1 см, то получится, что площадь фигуры равна n см².

За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.

Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.

Далее покажем, что подразумевается под площадью прямоугольника.

Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.

Называя величину площади, необходимо указывать единицу измерения.

Например, прямоугольник состоит из пятнадцати квадратов; площадь каждого квадрата составляет 1 см². Следовательно, площадь всего прямоугольника равна 15 см².

S = 15 см²

Решим задачу.

Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.

В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см² = 6 см · 7 см = АВ · ВС.

Поэтому можно ввести формулу для нахождения площади прямоугольника.

Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.

S = а · b

Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.

S = а · а = а²

Далее найдём соотношение между единицами измерения площадей.

Так как 1 см = 10 мм, следовательно, 1 см² = 10² мм² = 100 мм².

Соответственно, 1 дм² = 10² см² = 100 см²

1 м² = 10² дм² = 100 дм²

1 км² = 1000² м² = 1000000 м².

Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.

1 ар = 10² м² = 100 м²

Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.

1 га = 100² м² = 10000 м² = 100 а

Решим задачу.

Найдём площадь прямоугольника.

При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.

S (с недостатком) = 3 · 5 = 15 см²

Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.

S (с избытком) = 4 · 6 = 24 см²

Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.

15 см² < S < 24 см²

Отметим, что равные прямоугольники имеют равную площадь.

Сравним площади закрашенных квадратов, изображённых на рисунке.

Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.

Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.

Примеры заданий из Тренировочного модуля

№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?

Решение: Для нахождения площади квадрата воспользуемся следующей формулой:

S = а² = 5см · 5 см = 25 см²

№ 2. Найдите площадь фигуры.

Решение: сначала следует разделить фигуру на три прямоугольника, далее найти площадь каждого по формулеS=а · b, а затем сложить площади трёх фигур. Или можно найти площадь прямоугольника со сторонами 10 см и 3 см, она равна 30 см². Далее вычислить площадь вырезанной фигуры со сторонами 2см на 1 см, она составляет 2см². И вычесть 2 см² из 30см².

Ответ: 28 см².

Area of a rectangle is the region covered inside the boundaries of the rectangle. A rectangle is a quadrilateral in which opposite sides are equal and parallel. The diagonals of a rectangle are equal and are perpendicular bisectors to each other. All the angles of the rectangles are 90°. A rectangle is similar to a parallelogram. We can say that all the rectangles are parallelograms but its converse is not true.

Table of Contents:

• Definition
• Units
• Formula
• How to Calculate the Area of Rectangle
• Area by Diagonal
• Area by perimeter
• Derivation
• Solved Examples
• FAQS

What is the Area of a Rectangle?

Definition – The area of a Rectangle is the region occupied by a rectangle within its four sides or boundaries.

The area of a rectangle is the space enclosed by the boundaries of the rectangle. In general, the area of any shape is the space enclosed by the geometrical shape. We can also say that the space enclosed by the perimeter of the rectangle is the area of a rectangle. The perimeter of a rectangle is the sum of all the sides. For a rectangle, the area is the multiplication of its length by its breadth. The opposite sides of the rectangle are equal, and if the length and breadth are also equal, then the shape becomes a square. Therefore, every square is a rectangle. The below-given diagram shows the rectangle and its area,

Unit of Area of Rectangle

The area of a rectangle is measured in square units and the standard unit for measuring the area of a rectangle is m². Other units widely used for measuring the area of the rectangle are cm², mm², and others.

Side	Area
meter(m)	m2   or (meter)2
centimeter(cm)	cm2  or (centimeter)2

Area of a Rectangle Formula

The formula for the area of a rectangle is the multiplication of length (L) and breadth (B).

The formula of the Area of a Rectangle
Area of Rectangle	A = L x B

where ,
L is the length of the rectangle
B is the breadth of the rectangle

Note:-

If the unit of length and breadth is not exact then it should be transformed into one unit. For e.g. If the length is in cm and breadth in m then both dimensions should be adjusted either to m or cm.

How to Find the Area of a Rectangle?

The area of the rectangle is defined as the product of its length and breadth. Following are the steps that help calculate the area of the rectangle,

Step 1: Note down the dimensions of the rectangle.

Step 2: Calculate the product of the length and breadth of the rectangle.

Step 3: Write the answer in respective square units.

Example: Find the area of a rectangle whose length is 20 inches and breadth is 50 inches.

Solution:

The formula for area of rectangle is given:

Area = L × B

Area = 20 × 50

Area = 1000 inches²

Thus, the required area is 1000 inches²

Area of a Rectangle with Diagonal

The area of the rectangle can be found by two methods which are:

Method 1:

We can find the value of the missing side using the Pythagoras theorem and then find the area. Let us understand this using an example.

The diagonal of the rectangle is the line joining opposite vertices. The diagonal of the rectangle is calculated using Pythagoras’s Theorem

(Diagonal)² = (Length)² + (Breadth)²

Length² = (Diagonals² – Breadth²)

Length = √(Diagonals² – Breadth²)

The formula for the area of a rectangle is calculated by:

Area = Length × Breadth

Area = √(Diagonals² – Breadth²) × Breadth

Area = Breadth √(Diagonals² – Breadth²)

Method 2:

If both the diagonals of the rectangle are given then its area can be found with the help of the area of the quadrilateral formula.

Let a rectangle ABCD have diagonals as AC and BD and their length is d₁ and d₂ then its area is given by,

Area of rectangle ABCD = 1/2 × d₁ × d₂

Example: Find the area of a rectangle whose length of the diagonals is 10 cm and 14 cm.

Solution:

The formula for area of rectangle is,

Area = 1/2 × d₁ × d₂

Area = 1/2 × 10 × 14

Area = 70 cm²

Thus, the area of required rectangle is 70 cm².

Area of Rectangle using Perimeter

To calculate the area of a rectangle using the perimeter and one dimension follow the following steps,

Step 1: Note the perimeter and the given dimension.

Step 2: Use the perimeter formula to find the other dimension.

Step 3: Use the area of the rectangle formula and substitute the required value obtained in Step 2

Step 4: Simplify the expression and add unit²  to get the final answer.

The example given below explains the above concept.

Example: Find the area of a rectangle when the perimeter is 28 cm and the breadth is 8 cm.

Solution: 

Given,

Perimeter of Rectangle = 28 cm

length = 8 cm

breadth(b) = ?

Using Perimeter of rectangle formula,

Perimeter of rectangle = 2 (l + b)

28 = 2 (8 + b)

14 = 8 + b

b = 6 cm

Thus the breadth of rectangle is 6 cm

Area of Rectangle = l × b

= 8 × 6 = 48 cm²

Thus, the area of the Rectangle is 48 cm²

Derivation of Area of a Rectangle

The area of a rectangle is the product of length and breadth. This can be derived by dividing the rectangle into two triangles. The triangles are equal as the base and height of the two triangles will be equal. 

Let’s derive the formula for the area of a rectangle, the image given below shows that a rectangle is made by joining two equal right-angle triangles.

• Area of Rectangle = 2 (Area of Triangle)
• Area of Rectangle = 2 (1/2 × Base × Height)
• Area of Rectangle = 2 (1/2 × AB × BC)
• Area of Rectangle = AB × BC
• Area of Rectangle = Length × Breadth.

Thus, the area of the rectangle formula is derived.

Solved Examples on Area of Rectangle

Example 1: The length and width of a rectangle are 6 units and 3 units, respectively. Find the area of the rectangle.

Solution:

Given,  

length = 6 unit
breadth = 3 units

Area of rectangle =  length × breath
                            =  6 × 3
                            = 18 square units

Thus, the area of given rectangle is 18 square units

Example 2: Find the area of a rectangle whose height is 10 cm and width is 2 cm.

Solution: 

Given, 

Height = 10 cm
Width = 2 cm

Area of Rectangle = width × height

Area of Rectangle = 10 × 2 = 20

Therefore, the area of the rectangle is 20 cm².

Example 3: A rectangular panel has a width of 150 mm and a height of 99 mm. Find the area of this panel.

Solution: 

Given, 

Height = 99 mm 
            = 9.9 cm

Width = 150 mm = 15 cm

Area of Rectangle = width × height

Area of Rectangle = 15 × 9.9

Therefore, the area of the rectangle = 148.5 cm².

Example 4: The height of a rectangular net is seen to be 20 cm. Its area is seen to be 260 cm². Find the width of the provided net.

Solution: 

Given, 

Height = 20 cm
Area = 260 cm²

Area of Rectangle = width × height

Therefore, 

width = Area / height

width = 260/20

width = 13 cm

Thus, the width of the rectangle is 13 cm

Example 5: The height and width of a rectangular desk are 40 m and 20 m, respectively. If a carpenter charges ₹ 2 per m² for his work, how much would it cost to make the whole desk?

Solution:

Given, 

Height of Desk = 40 m
Width of Desk = 20 m

Area of top of Desk = width of desk × height of desk

Area of top of Desk = 40 × 20

Area of top of Desk = 800 m²

At the cost of ₹ 2 per m², 

The cost for making top of the desk is 800 × 2 = ₹ 1600

Example 6: A wall whose length and width are 60 m and 40 m respectively needs to be painted. Find the quantity of the paint required if 1 litre of paint can paint 400 m² of the wall.

Solution:

Given, 

Length of wall = 60 m

Width of wall = 40 m

Area of wall = width × length

Area of wall = 60 × 40

Area of wall = 2400 m²

Paint required for 400 m² of wall = 1 litre   (given)

Paint required for 2400 m² of wall = 2400 / 400 × 1 = 6 litre.

Thus, the paint required to paint the wall is 6 litre.

Q7: If the length and breadth of the rectangular glass slab are 6 m and 4 m respectively. Then finds its area.

Solution:

Length of the rectangular slab is 6 m

Breadth of the rectangular slab is 4 m

Area of rectangular slab = length × breadth

                                       = 6 × 4
                                       = 24 m²

Here, the area is measured in m².

Related Articles:

• Area of Square
• Area of a Triangle
• Area of Circle
• Area of Quadrilateral
• Area of Rhombus
• Area of Trapezium
• Area of Parallelogram

FAQs on Area of Rectangle

Q1: What is the formula for the area of a rectangle?

Answer:

Area (A) of rectangle formula is the product of the length and breadth. It can be defined as the space occupied by its boundaries.

Q2: What is the unit of area of a rectangle?

Answer:

The unit of the area of rectangle are meter², centimeter², inches², etc. In general, it is unit².

Q3: What is the perimeter of a rectangle?

Answer:

The perimeter of rectangle is the sum of the length of all its boundaries. The formula for perimeter of rectangle is given as;

P = 2 (Length + Breadth)

Q4: How to find the area of a rectangle?

Answer:

For a rectangle whose length is l and breadth is b then its area can be calculated by using the formula,

Area = l × b

Q5: How to find the area of a rectangle with a diagonal?

Answer:

The area of the rectangle when its diagonal is given is calculated using the formula,

Area = 1/2 × d₁ × d₂

where
d₁ is the first diagonal.
d₂ is the second diagonal.

Q6: How to find the area of a rectangle when a perimeter is given?

Answer:

The area of a rectangle when its perimeter and any one side is given can be calculated by,

Step 1: Use the perimeter of the rectangle formula to find the relation between length (l) and breadth (b).

Step 2: One dimension is already given. Use the relation to find the other dimension.

Step 3: When both dimensions are known use the area formula to find the area.

Q7: How to calculate the area of a quadrilateral with 4 different sides?

Answer:

The area of a quadrilateral with all fours sides different and both diagonal given are, 

Area = 1/2 × d₁ × d₂

where
d₁ is the first diagonal.
d₂ is the second diagonal.

Q8: Is the area of a rectangle equal to the area of a square?

Answer:

No, it is not necessary that the area of the rectangle is equal to the area of square. The condition where both the areas are equal is when the length and breadth in a rectangle are equal.

Вернуться к содержанию рабочей тетради

Внетабличное умножение и деление

---

Вернуться к содержанию рабочей тетради

---