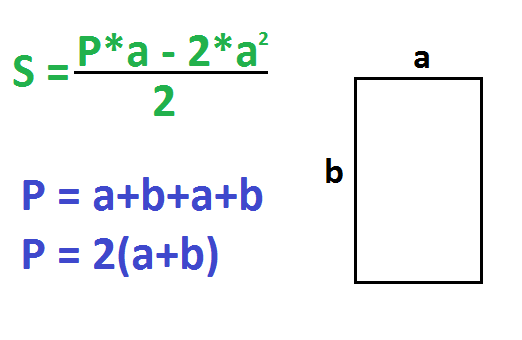Как можно найти площадь прямоугольника по диагонали

Как можно найти площадь прямоугольника по диагонали

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

  • S — искомая площадь прямоугольника;
  • a и b — соседние стороны.

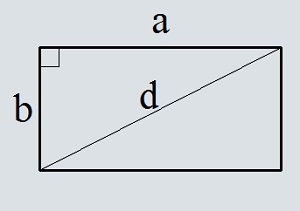
2. Если известны любая сторона и диагональ

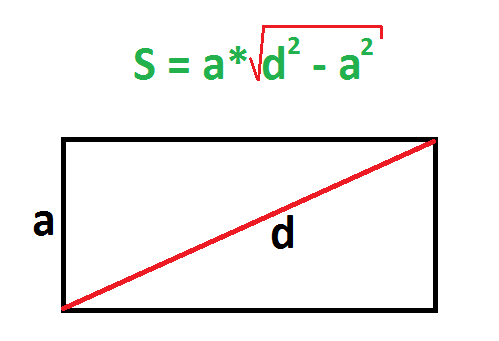
Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

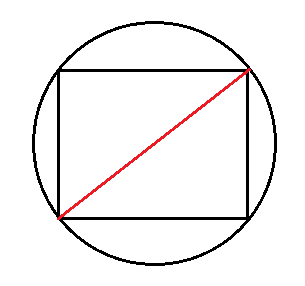
3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • D — диаметр описанной окружности.

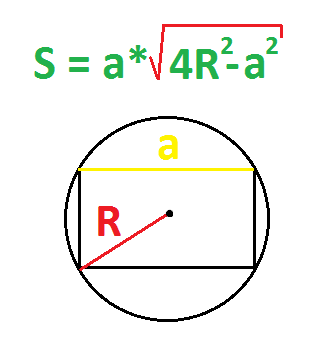
4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • d — любая диагональ прямоугольника;
  • α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • R — радиус описанной окружности;
  • α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

  • ТЕСТ:​ ​​Умеете ли вы считать в уме?
  • Как легко и быстро считать проценты в уме
  • Как найти площадь любого треугольника
  • ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
  • Как освоить устный счёт школьникам и взрослым
Источник

Площадь прямоугольника через диагональ

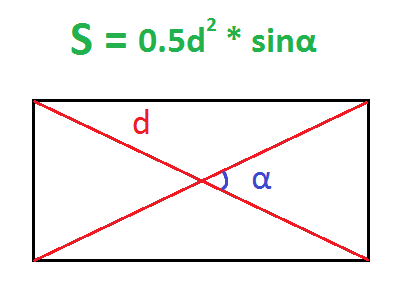
В прямоугольнике диагонали равны между собой. Если известен угол α между диагоналями (длина диагоналей равна d), то площадь прямоугольника можно найти по формуле:

Sпр = 0,5 * d² * sinα.

Например, если угол между диагоналями равен 30°, а диагонали равны 5 см, то площадь будет равна:

Sпр = 0,5 * 25 * 0,5 = 6,25 см.

Если неизвестен угол между диагоналями, то будет нужно найти стороны прямоугольника. А затем воспользоваться формулой:

Sпр = a * b.

Как известно, диагональ прямоугольника делит его на 2 равных прямоугольных треугольника. Поэтому задача сводится к тому, чтобы найти катеты прямоугольного треугольника через гипотенузу.

Кроме длины диагонали требуется знать либо одну из сторон прямоугольника, либо отношение сторон, либо угол между стороной и диагональю.

1) Если известна диагональ (пусть она будет равна d) и одна из сторон (например, b), то выражаем неизвестную сторону из формулы:

a² + b² = c² -> a = √(c² – b²).

Sпр = a * b = √(c² – b²) * b.

Например, если диагональ d = 5 см и сторона b = 3 см, то a = √(25 – 9) = √16 = 4 см.

Площадь прямоугольника равна 3 * 4 = 12 см.

2) Если известно отношение сторон, то задача сводится к нахождению обеих сторон через составление уравнения.

Например, если стороны относятся как 2:3, а диагональ равна 13 см, то можно составить уравнение:

(2x)² + (3x)² = 4x² + 9x² = 169.

13x² = 169.

x = √13.

Значит, a = 2√13 см и b = 3√13 см.

Площадь прямоугольника равна 2√13 * 3√13 = 6 * 13 = 78 см.

3) Если известна диагональ и один из прилежащих к диагонали углов, то нужно воспользоваться формулами:

a = d * cosβ (β – прилежащий угол) и b = d * sinα (α – противолежащий угол).

Например, d = 10 см и угол α = 30°.

a = 10 * cos30° = 10√3 / 3.

b = 10 * sin30° = 5 см.

Площадь прямоугольника равна 5 * (10√3 / 3) ≈ 28,33 см.

Источник


Download Article


Download Article

When you’re working with rectangles, you can find out a lot of information about them just by knowing a few key points of information. If you’ve been given the length of the diagonal and at least one side, you can calculate the area of the whole shape with just a few equations. Always use a calculator to check your math, and don’t forget to add your units onto the answer!

  1. Image titled Find the Area of a Rectangle Using the Diagonal Step 1

    1

    Mark the diagonal on the rectangle. If you have a visual of your rectangle, it will be a lot easier to figure out the area given a diagonal. Draw out a rectangle (it doesn’t have to match the proportions given, just a rectangle shape will do) and mark out a diagonal line to create 2 triangles.[1]

    • You’ll be able to see the 2 triangles that make up the rectangle now.

  2. Image titled Find the Area of a Rectangle Using the Diagonal Step 2

    2

    Advertisement

  3. Image titled Find the Area of a Rectangle Using the Diagonal Step 3

    3

  4. Image titled Find the Area of a Rectangle Using the Diagonal Step 4

    4

  5. Image titled Find the Area of a Rectangle Using the Diagonal Step 5

    5

    Plug the new number into A=ltimes w. To find the area of your entire rectangle, you need to solve for Area = length x width, or A = l x w. Now that you’ve used the Pythagorean Theorem to find the second side length, you can solve for the area. Don’t forget your units![5]

    6. Advertisement

  1. Image titled Find the Area of a Rectangle Using the Diagonal Step 6

    1

    Mark the diagonal and side length on your rectangle. If you have a visual in front of you, it will be much easier to see how you’re solving your equation. Draw a simple rectangle with a ruler and create a diagonal line across it to make 2 triangles.[6]

    • It’s not mandatory to draw your triangle, but it can help you, especially if you’re just starting out.

  2. Image titled Find the Area of a Rectangle Using the Diagonal Step 7

    2

    Enter the length and diagonal into {displaystyle A=ltimes {sqrt {d^{2}-l^{2}}}}. Simply plug the length and the diagonal into the formula above. Remember, the diagonal is always longer than the length of the rectangle. [7]

    • For example, if the length is 8 inches and the diagonal is 10 inches, the formula would be {displaystyle A=8times {sqrt {10^{2}-8^{2}}}}.

  3. Image titled Find the Area of a Rectangle Using the Diagonal Step 8

    3

    4. Advertisement

Add New Question

  • Question

    If the diagonal of a rectangle is10cm then what is its area?

    Community Answer

    You don’t have enough information to solve.

  • Question

    A rectangle with diagonal of 20 cm has sides in the ratio 2:1. How do I find the area of rectangle?

    Donagan

    Such a rectangle would have its sides and diagonal in the ratio of 2:1:√5 (per the Pythagorean theorem). The ratio of √5 to the diagonal (20) is equal to the ratio of 2 to the longer side (or the ratio of 1 to the shorter side). Thus √5 : 20 = 2 : x, where x is the longer side. Expressed as fractions, that’s √5 / 20 = 2 / x. Cross-multiplying: (√5)(x) = (20)(2). Dividing by √5: x = 40 / √5 = 40 / 2.236 = 17.9 cm. The shorter side is half that, or 8.94 cm.

  • Question

    If the side = 48 meters and the diagonal = 50 meters, how do I find the area of the rectangle?

    Donagan

    Let s be the shorter side. Then (by the Pythagorean Theorem) s² + 48² = 50². So s² + 2304 = 2500. Then s² = 196, and s = 14 m. The area is 48 x 14 = 672 square meters.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

  • If all you know is the length of the diagonal, you can calculate the area of a square, but not a rectangle.

  • To find the area of a rectangle, you need to know the diagonal and at least one side length.

  • You can also use an online calculator, like Omni Calculator, to check your work.

Advertisement

References

About This Article

Thanks to all authors for creating a page that has been read 138,185 times.

Did this article help you?

Источник

Площадь прямоугольника по диагонали и стороне

Калькулятор рассчитывает площадь прямоугольника по диагонали и стороне.

Площадь прямоугольника по диагонали и стороне

Введите диагональ d

Введите сторону a

Формула площади прямоугольника по диагонали и стороне

Где a – сторона прямоугольника,
d – диагональ прямоугольника

Вывод формулы площади прямоугольника по диагонали и стороне

Площадь прямоугольника по диагонали и стороне

Так как диагональ делит прямоугольник на 2 прямоугольных треугольника. В которых диагональ является гипотенузой а сторона катетом. Исходя из этого по теореме Пифагора вычислим сторону b.

Подставим полученную сторону в формулу площади прямоугольника

Похожие калькуляторы

Источник

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

11 346

Как найти площадь прямоугольника – 9 формул с примерами

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

  1. Найти квадрат диагонали, то есть умножить ее на саму себя.
  2. Найти квадрат известной стороны.
  3. Из квадрата диагонали вычесть квадрат стороны.
  4. Найти квадратный корень получившейся разности.
  5. Умножить его на известную сторону.

Ищем площадь по диагонали и стороне

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

  1. Квадрат стороны = 3*3 = 9 см.
  2. Квадрат диагонали = 5*5 = 25 см.
  3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
  4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
  5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

  1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
  2. Найдите квадрат известной стороны.
  3. Отнимите от квадрата диаметра квадрат стороны.
  4. Найдите квадратный корень разности.
  5. Умножьте квадратный корень на известную сторону.

По одной стороне и диаметру окружности

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

  1. Квадрат диаметра: 10*10 = 100 см.
  2. Квадрат стороны: 8*8 = 64 см.
  3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
  4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
  5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

Диагональ равна диаметру

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

  1. Найти квадрат радиуса (умножьте радиус на радиус).
  2. Умножить квадрат радиуса на 4.
  3. Найти квадрат известной стороны.
  4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
  5. Найти квадратный корень разности.
  6. Умножить корень на известную сторону.

Площадь по стороне и радиусу

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

  1. Квадрат радиуса: 5*5=25 см.
  2. Четыре квадрата радиуса: 4*25 = 100 см.
  3. Квадрат стороны: 6*6 = 36 см.
  4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
  5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
  6. Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из  сторон равна 3 см. Найдите площадь.

  1. Нахожу вторую сторону прямоугольника:
    1. P=2(a+b).
    2. P=2a+2b.
    3. 14= 2*3+2b.
    4. 14 = 6+2b.
    5. 2b = 14-6 = 8.
    6. b = 8/2.
    7. b = 4.
  2. Нахожу площадь по основной формуле. S = 3*4 = 12 см.

Ответ: 12 см.

По стороне и периметру – 2 способ

Действия такие:

  1. Умножьте периметр на сторону.
  2. Найдите квадрат стороны.
  3. Умножьте квадрат стороны на 2.
  4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
  5. Поделите на 2.

Как найти площадь, если известны периметр и сторона

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

  1. Умножаю периметр на сторону: 8*28 = 224 см.
  2. Нахожу квадрат стороны: 8*8 = 64 см.
  3. Умножаю квадрат стороны на два: 64*2 = 84 см.
  4. Отнимаю из первого третье: 224-84 = 140 см.
  5. Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

  1. Найти квадрат диагонали (умножить диагональ на саму себя).
  2. Найти половину этого квадрата – умножить его на 0,5.
  3. Найти синус угла между диагоналями.
  4. Умножить половину квадрата диагонали на синус угла между диагоналями.

Ищем площадь по диагонали и углу

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

  1. Квадрат диагонали: 10*10 = 100 см.
  2. Половина этого квадрата: 0,5*100 = 50 см.
  3. Синус угла между диагоналями: sin 30 градусов = 0,5.
  4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

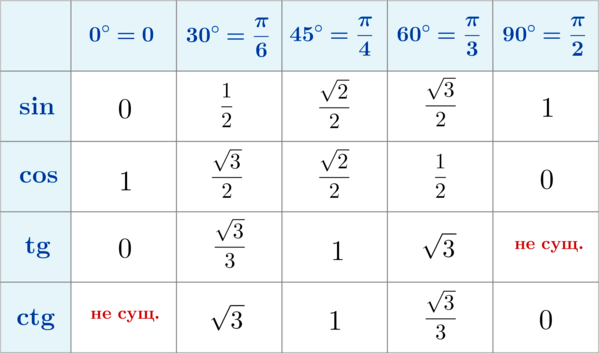
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

Основные значения из тригонометрии

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

  1. Находим длину диагонали: 6*2 =12 см.
  2. Квадрат диагонали равен 144 см.
  3. Половина квадрата: 72 см.
  4. Синус 30 градусов равен 0,5.
  5. Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.

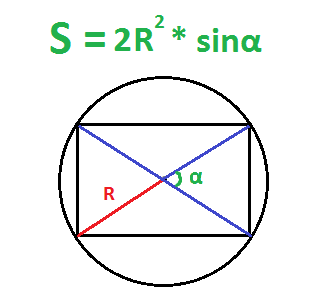
По радиусу описанной окружности и углу между диагоналями – второй способ

Действия:

  1. Найти квадрат радиуса (умножить радиус на радиус).
  2. Умножить квадрат радиуса на два.
  3. Найти синус угла между диагоналями.
  4. Умножить синус угла на два радиуса в квадрате.

Ищем площадь по радиусу и углу между диагоналями

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

  1. Квадрат радиуса: 6*6 = 36.
  2. Два радиуса в квадрате: 36*2 = 72.
  3. Синус 30 градусов равен 0,5.
  4. Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Ответ: 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

( 1 оценка, среднее 5 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

ПОДПИСАТЬСЯ

Источник

Добавить комментарий