Как можно найти площадь ромба по формуле

Как можно найти площадь ромба по формуле

Площадь ромба через сторону и угол

{S = a^2 cdot sin (alpha)}

На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора

Содержание:
  1. калькулятор площади ромба
  2. формула площади ромба через сторону и угол
  3. формула площади ромба через сторону и высоту
  4. формула площади ромба через диагонали
  5. формула площади ромба через угол и диагональ из угла
  6. формула площади ромба через угол и противолежащую диагональ
  7. формула площади ромба ромба через радиус вписанной окружности и угол
  8. формула площади ромба через радиус вписанной окружности и сторону
  9. примеры задач

Формула площади ромба через сторону и угол

Площадь ромба через сторону и угол

S = a^2 cdot sin (alpha)

a – сторона ромба

α – угол между сторонами ромба

Формула площади ромба через сторону и высоту

Площадь ромба через сторону и высоту

S = a cdot h

a – сторона ромба

h – высота ромба

Формула площади ромба через диагонали

Площадь ромба через диагонали

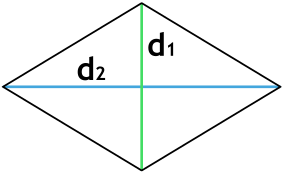
S = dfrac{d_1 cdot d_2}{2}

d1 и d2 – диагонали ромба

Формула площади ромба через угол и диагональ из угла

Площадь ромба через угол и диагональ из угла

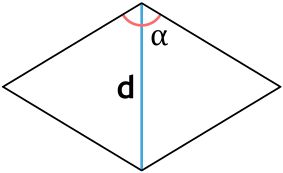
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})

d – диагональ ромба

α – угол между сторонами ромба, из которого выходит диагональ

Формула площади ромба через угол и противолежащую диагональ

Площадь ромба через угол и противолежащую диагональ

S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})

d – диагональ ромба, противоположная углу α

α – угол между сторонами ромба

Формула площади ромба через радиус вписанной окружности и угол

Площадь ромба через радиус вписанной окружности и угол

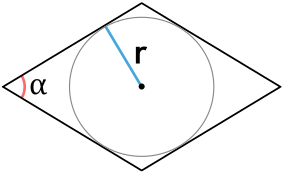
S = dfrac{4r^2}{sin(alpha)}

r – радиус окружности

α – угол между сторонами ромба

Формула площади ромба через радиус вписанной окружности и сторону

Площадь ромба через радиус вписанной окружности и сторону

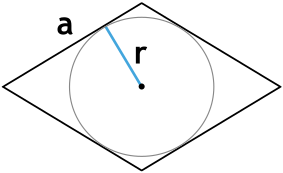
S = 2ar

r – радиус окружности

a – сторона ромба

Примеры задач на нахождение площади ромба

Задача 1

Найдите площадь ромба если его диагонали равны 34 и 4.

Решение

Для решения задачи воспользуемся формулой площади ромба через диагонали.

S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2

Ответ: 68 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь ромба если его диагонали равны 4 и 6.

Решение

Задача аналогична предыдущей.

S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2

Ответ: 12 см²

Проверим ответ на калькуляторе .

Задача 3

Найдите площадь ромба стороны которого равны 5, а высота равна 4.

Решение

Воспользуемся формулой площади ромба через высоту и сторону.

S = a cdot h = 5 cdot 4 = 20 : см^2

Ответ: 20 см²

Проверим полученный ответ на калькуляторе .

Источник
Определение ромба

Ромб — это параллелограмм, в котором все стороны равны друг другу.

Онлайн-калькулятор площади ромба

Если стороны ромба образуют прямой угол, то получим квадрат.

Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.

Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.

Формула площади ромба по стороне и высоте

Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.

S=a⋅hS=acdot h

aa — сторона;
hh — высота, опущенная на сторону aa.

Решим простой пример.

Пример

площадь ромба по стороне и высоте

Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.

Решение

a=5a=5
h=2h=2

Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)

Ответ: 10 см. кв.

Формула площади ромба через диагонали

Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.

S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2

d1,d2d_1, d_2 — диагонали ромба.

Пример

площадь ромба через диагонали

Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.

Решение

d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1

Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)

Ответ: 49 см. кв.

Формула площади ромба через две стороны и угол между ними

S=a2⋅sin⁡(α)S=a^2cdotsin(alpha)

aa — сторона ромба;
αalpha — любой угол ромба.

Пример

площадь ромба через две стороны и угол между ними

Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.

Решение

a=10a=10
α=30∘alpha=30^{circ}

По формуле получаем:
S=a2⋅sin⁡(α)=100⋅sin⁡(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)

Ответ: 50 см. кв.

Формула площади ромба по радиусу вписанной окружности и углу

S=4⋅r2sin⁡(α)S=frac{4cdot r^2}{sin(alpha)}

rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.

Пример

по радиусе вписанной окружности и угле

Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).

Решение

r=4r=4
α=60∘alpha=60^{circ}

S=4⋅r2sin⁡(α)=4⋅16sin⁡(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)

Ответ: 73.9 см. кв.

Формула площади ромба по радиусу вписанной окружности и стороне

S=2⋅a⋅rS=2cdot acdot r

aa —сторона ромба;
rr — радиус вписанной окружности в ромб.

Пример

По радиусе вписанной окружности и стороне

Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.

Решение

a=5a=5
r=4r=4

S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)

Ответ: 40 см. кв.

Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!

Тест на тему “Площадь ромба”

Источник

Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.

  • Формула вычисления площади

    • По длине стороны и высоте

    • По длине стороны и углу

    • По длинам диагоналей

  • Примеры задач

Формула вычисления площади

По длине стороны и высоте

Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

Площадь ромба

По длине стороны и углу

Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:

S = a 2 ⋅ sin α

Площадь ромба

По длинам диагоналей

Площадь ромба равна одной второй произведения его диагоналей.

S = 1/2 ⋅ d1 ⋅ d2

Площадь ромба

Примеры задач

Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.

Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.

Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.

Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.

Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.

Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.

Источник

Содержание:

  • Формулы площади ромба:
  • Формула периметра ромба:

Ромб

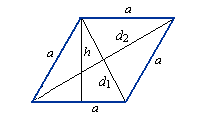
Ромб – это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.

Формулы площади ромба:

Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

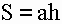
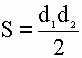
Площадь ромба, 1-ая формула площади ромбаПлощадь ромба, 2-ая формула площади ромба

S – площадь ромба

a – длина основания ромба

h – длина высоты ромба

d1 – длина 1-ой диагонали

d2 – длина 2-ой диагонали

См. также: Программа для расчета площади ромба.

Формула периметра ромба:

Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.

1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).

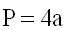
Периметр ромба, формула периметра ромба

P – периметр ромба

a – длина стороны ромба

Остались вопросы?

Здесь вы найдете ответы.

Что понимается под высотой ромба?

Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.

Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?

Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.

Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:

BAH=180-30-90=60 градусов.

Так, угол АВС равен:

ABC=180-60=120 градусов.

Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?

Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:

S = a*h.

Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:

h = S/a.

Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?

Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:

SΔ = 4*3/2 = 6 см.кв.

Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:

S = 5*x = 6 см.кв.

Отсюда можно найти значение х:

х = 6/5 = 1,2 см.

Ответ: высота ромба составляет 1,2 см.

Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?

Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:

с = √(9+16) = √25 = 5 см.

Следовательно, сторона ромба также равна 5 см.

Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:

S = d1*d2/2 = 6*8/2 = 24 см. кв.

Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):

S = a*h

Из данной формулы выражаем высоту:

h = S/a = 24/5 = 4,8 см.

Ответ: Высота ромба составляет 4,8 см.

Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?

Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:

h = (d1 * d2)/a

Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?

Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:

Р = а+а+а+а

В данном случае периметр ромба равен 48 см., это значит, что:

а+а+а+а = 48 см.

Находим значение а:

а = 48/4 = 12 см.

Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:

S = а*h

В задании сказано, что площадь ромба – 60 см.кв. Значит:

а*h=60

Находим неизвестную высоту:

h=60/а=60/12=5 см.

Ответ: Высота ромба – 5 см.

Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?

Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:

а = Р/4 = 32/4 = 8 см.

Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:

S = а* h

В конкретном случае:

48 = 8* h

Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:

H = 48/8 = 6 см.

Ответ: Высота ромба составляет 6 см.

Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?

Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:

Р = 4*а

По условию задачи:

52 = 4*а

Следовательно:

а = 52/13 = 13 см.

Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:

10х:24х=10:24

Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.

Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:

с2 = а2 + b2

Для данной задачи это равенство записывается так:

(5х)²+(12х)²=13²

Отсюда видно, что:

169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.

Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).

Площадь (S) ромба рассчитывается как:

S = d₁*d₂/2 или a·h

Из этого можно составить следующее уравнение:

d₁*d₂=2a*h

Выражаем h и получаем:

h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.

Какая формула используется с целью вычисления высоты ромба?

Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.

Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.

Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.

В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:

h = a*a*sin A /a = a*sin A.

Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.

В каком виде записываются формулы, используемые для определения площади
ромба?

Площадь ромба можно рассчитать одним из трех способов:

1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.

2. S = ah, или Длина стороны ромба, умноженная на его высоту.

3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.

На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?

Зная, чему равен периметр ромба, можно вычислить длину его стороны:

Р/4 = 8 см.

Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:

h = 8-1,7 = 6,3 см.

Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:

8 * 6,3 = 50,4 см².кв.

Ответ: S = 50,4 см. кв.

Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?

Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:

(4d)²+(3d)²=10² = 16d²+9d² = 100

Отсюда:

25d²=100

d =2,

Значит:

d¹/2 = 4d = 8 см.

d²/2 = 3d = 6 см.

Теперь можно найти площадь:

S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.

Ответ: S ромба = 96 см.кв.

Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?

Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:

S = ½ d1*d2.

Как записать формулу вычисления площади ромба через диагонали?

Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.

Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:

S = ½ d1*d2.

Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:

S=1/2*5*4=10 см. кв.

Как выглядит формула для определения площади ромба?

S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:

S=a*h.

См. также: Программа для расчета периметра ромба.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

У этого термина существуют и другие значения, см. Ромб (значения).

Rhombus.svg

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1] (см. другие варианты определенияПерейти к разделу «Признаки»).

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства[править | править код]

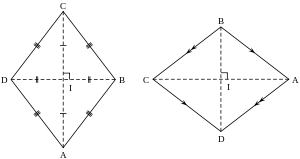
  • Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
  • Высоты в ромбе равны между собой.
  • Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре конгруэнтных прямоугольных треугольника.
  • Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
  • Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
  • Середины четырёх сторон ромба являются вершинами прямоугольника.
  • Диагонали ромба являются осями его симметрии.
  • В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки[править | править код]

Самое общее определение: ромб — это выпуклый четырёхугольник[2], все стороны которого равны друг другу. Можно показать, что такой четырёхугольник является параллелограммом[3][1].

Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[4]:

  • Две его смежные стороны равны (отсюда следует, что все стороны равны).
  • Его диагонали пересекаются под прямым углом.
  • Одна из диагоналей делит содержащие её углы пополам. Другими словами, диагональ является биссектрисой противоположных углов.
  • Диагонали параллелограмма делят его на четыре равных между собой треугольника.
  • Диагонали параллелограмма являются осями симметрии[5].

Помимо всего, ромб можно рассматривать как частный случай дельтоида, у которого любые две смежные стороны равны между собой.

Квадрат как частный случай ромба[править | править код]

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[6][7].

Уравнение ромба[править | править код]

К уравнению ромба (центр в начале координат)

Уравнение ромба с центром в точке {displaystyle {x_{0},y_{0}}} и диагоналями, параллельными осям координат, может быть записано в виде[8]:

{displaystyle {frac {|x-x_{0}|}{a}}+{frac {|y-y_{0}|}{b}}=1,}

где a,b — половины длин диагоналей ромба по осям X,Y соответственно.

Длина стороны ромба равна {displaystyle {sqrt {a^{2}+b^{2}}}.} Площадь ромба равна {displaystyle 2ab.} Левый угол ромба рассчитывается по формуле:

{displaystyle 2operatorname {arctg} {frac {b}{a}}}

Второй угол дополняет его до 180°.

В случае a = b уравнение отображает повёрнутый на 45° квадрат:

{displaystyle |x-x_{0}|+|y-y_{0}|=a,}

где сторона квадрата равна {displaystyle a{sqrt {2}},} а его диагональ равна {displaystyle 2a.} Соответственно площадь квадрата равна {displaystyle 2a^{2}.}

Из уравнения видно, что ромб можно рассматривать[8] как суперэллипс степени 1.

Площадь ромба[править | править код]

Rhombus1.svg

  • Площадь ромба равна половине произведения его диагоналей.
{displaystyle S={dfrac {ACcdot BD}{2}}}
  • Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
{displaystyle S=acdot h}
  • Кроме того, площадь ромба может быть вычислена по формуле:
{displaystyle S=a^{2}cdot sin alpha },

где alpha  — угол между двумя смежными сторонами ромба.

  • Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол alpha :
{displaystyle S={dfrac {4r^{2}}{sin alpha }};}
  • Площадь ромба равна удвоенному произведению стороны и радиуса вписанной окружности:
{displaystyle S=2ar.}

Радиус вписанной окружности[править | править код]

Радиус вписанной окружности r может быть выражен через диагонали p и q в виде[9]:

{displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}}.}

В геральдике[править | править код]

Ромб является простой геральдической фигурой.

  • Червлёный ромб в серебряном поле

    Червлёный ромб в серебряном поле

  • В червлёном поле 3 сквозных ромба: 2 и 1

    В червлёном поле 3 сквозных ромба: 2 и 1

  • Просверленный червлёный ромб в серебряном поле

    Просверленный червлёный ромб в серебряном поле

  • В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

    В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

Симметрия[править | править код]

Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

  • Ромбический орнамент

    Ромбический орнамент

  • Ромбические звёзды

    Ромбические звёзды

  • Более сложный орнамент

    Более сложный орнамент

  • Мозаика Пенроуза

См. другие примеры на Викискладе.

См. также[править | править код]

  • Дельтоид
  • Звезда (геометрия)
  • Ромбододекаэдр
  • Ромбоид

Примечания[править | править код]

  1. ↑ 1 2 Элементарная математика, 1976, с. 435..
  2. ↑ Требование выпуклости нужно, чтобы исключить случаи вырожденного четырёхугольника, у которого часть вершин совпадают (например, фигура, имеющая вид буквы V и ромбом не являющаяся).
  3. ↑ Погорелоа А. В. Домашняя работа по геометрии за 8 класс. М.: Просвещение, 2001, С. 18.
  4. ↑ Элементарная математика, 1976, с. 435—436..
  5. ↑ Шахмейстер А. Х. Треугольники и параллелограммы // Геометрические задачи на экзаменах. Часть 1. Планиметрия : книга / А. Х. Шахмейстер. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2015. — С. 26. — 392 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-98712-083-5. — ISBN 978-5-91673-155-2. — ISBN 978-5-4439-0347-7.
  6. ↑ Ромб // Малый академический словарь. — М.: Институт русского языка Академии наук СССР. Евгеньева А. П.. 1957—1984.
  7. ↑ Чудинов А. Н. Ромб // Словарь иностранных слов, вошедших в состав русского языка. 1910.
  8. ↑ 1 2 Weisstein, Eric W. Superellipse (англ.) на сайте Wolfram MathWorld. Здесь ромб назван diamond.
  9. ↑ Weisstein, Eric W. Rhombus (англ.) на сайте Wolfram MathWorld.

Литература[править | править код]

  • Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Источник

Добавить комментарий