Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 декабря 2021 года; проверки требуют 15 правок.
Рабо́та вы́хода — разность значений энергий уровня вакуума 

Работа выхода обычно указывается в электрон-вольтах, типичные величины лежат в диапазоне 3—5 эВ.
Возможные обозначения: 


Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам, достаточным чтобы электрон прошёл весь двойной слой, но достаточно близко по сравнению с размерами макроскопических граней кристалла.
Определение и комментарий[править | править код]
Работа выхода 

При удалении электрона от поверхности его взаимодействие с зарядами, остающимися внутри твёрдого тела, приводит к индуцированию поверхностных зарядов (в электростатике для расчёта взаимодействия применяется «метод изображения заряда»). Удаление электрона на бесконечность происходит в поле индуцированного поверхностного заряда на что требуется дополнительная работа, зависящая от диэлектрической проницаемости вещества, геометрии образца и свойств всех его поверхностей.
При нахождении величины 


Работа выхода в фотоэффекте[править | править код]
Работа выхода во внешнем фотоэффекте — минимальная энергия фотонов, необходимая для удаления электрона из вещества под действием света при 
Работа выхода из различных металлов[править | править код]
Единицей измерения работы в СИ являются джоуль (Дж), но в физике твердого тела принято использовать электронвольт (эВ)[1].
Диапазоны изменения работы выхода для типичных кристаллографических плоскостей указаны в таблице[2]:
| Элемент | эВ | Элемент | эВ | Элемент | эВ | Элемент | эВ | Элемент | эВ |
|---|---|---|---|---|---|---|---|---|---|
| Ag: | 4,52 — 4,74 | Al: | 4,06 — 4,26 | As: | 3,75 | Au: | 5,1 — 5,47 | B: | ~4,45 |
| Ba: | 2,52 — 2,7 | Be: | 4,98 | Bi: | 4,31 | C: | ~5 | Ca: | 2,87 |
| Cd: | 4,08 | Ce: | 2,9 | Co: | 5 | Cr: | 4,5 | Cs: | 2,14 |
| Cu: | 4,53 — 5,10 | Eu: | 2,5 | Fe: | 4,67 — 4,81 | Ga: | 4,32 | Gd: | 2,90 |
| Hf: | 3,9 | Hg: | 4,475 | In: | 4,09 | Ir: | 5,00 — 5,67 | K: | 2,29 |
| La: | 3,5 | Li: | 2,93 | Lu: | ~3,3 | Mg: | 3,66 | Mn: | 4,1 |
| Mo: | 4,36 — 4,95 | Na: | 2,36 | Nb: | 3,95 — 4,87 | Nd: | 3,2 | Ni: | 5,04 — 5,35 |
| Os: | 5,93 | Pb: | 4,25 | Pd: | 5,22 — 5,6 | Pt: | 5,12 — 5,93 | Rb: | 2,261 |
| Re: | 4,72 | Rh: | 4,98 | Ru: | 4,71 | Sb: | 4,55 — 4,7 | Sc: | 3,5 |
| Se: | 5,9 | Si: | 4,60 — 4,85 | Sm: | 2,7 | Sn: | 4,42 | Sr: | ~2,59 |
| Ta: | 4,00 — 4,80 | Tb: | 3,00 | Te: | 4,95 | Th: | 3,4 | Ti: | 4,33 |
| Tl: | ~3,84 | U: | 3,63 — 3,90 | V: | 4,3 | W: | 4,32 — 5,22 | Y: | 3,1 |
| Yb: | 2,60[3] | Zn: | 3,63 — 4,9 | Zr: | 4,05 |
Работу выхода можно определить методом контактной разности потенциалов, основанном на сравнении работ выхода из металлов – эталонного и контролируемого[4].
Работа выхода для полупроводника[править | править код]

Для полупроводников работа выхода определяется точно так же, как и для металлов (и данные для некоторых собственных полупроводников включены в таблицу).
На практике полупроводник обычно легирован и величина 





Более универсальной величиной, вместо 

Примечания[править | править код]
- ↑ Работа выхода может зависеть от грани монокристалла или от от преобладающей грани на поверхности текстуры металла. К примеру, Ag: 4,26; Ag(100): 4,64; Ag(110): 4,52; Ag(111): 4,74.
- ↑ CRC Handbook of Chemistry and Physics 97th edition (2016—2017), раздел 12, стр 123.
- ↑ Nikolic, M. V.; Radic, S. M.; Minic, V.; Ristic, M. M. The dependence of the work function of rare earth metals on their electron structure (англ.) // Microelectronics Journal : journal. — 1996. — February (vol. 27, no. 1). — P. 93—96. — ISSN 0026-2692. — doi:10.1016/0026-2692(95)00097-6. (недоступная ссылка)
- ↑ Метод контактной разности потенциалов.
Литература[править | править код]
- Solid State Physics, by Ashcroft and Mermin. Thomson Learning, Inc, 1976
- Гончаренко В.И., Олешко В.С. Метод контактной разности потенциалов в оценке энергетического состояния поверхности металлических деталей авиационной техники: монография. – М.: Изд-во МАИ, 2019. – 160 с. – ISBN 978-5-4316-0631-1 http://elibrary.mai.ru/MegaPro/UserEntry?Action=Link_FindDoc&id=68387&idb=0
Цель работы:
Изучение
явления термоэлектронной эмиссии и
определение работы выхода электрона
из металла.
Приборы и
принадлежности:
Панель с собранной электрической схемой,
набор цифровых вольтметров, амперметров
и миллиамперметров для измерения
анодного напряжения накала и тока
накала.
Теоретическое
введение.
В металле при
нормальной температуре имеется некоторое
количество электронов, энергия которых
достаточна для того, чтобы преодолеть
потенциальный барьер, имеющийся на
границе металла, и покинуть его
поверхность. При повышении температуры
металла число таких электронов резко
возрастает и делается вполне заметным.
Выход электронов из металла вследствие
нагревания последнего называется
термоэлектронной эмиссией. Величина
же энергии, которую необходимо сообщить
электрону для того, чтобы он покинул
поверхность металла, от состояния
поверхности, в частности, от ее чистоты
(подобрать надлежащим образом покрытые
поверхности, можно сильно снизить работу
выхода, например оксидированием чистого
металла).
В данной работе,
используя метод прямых Ричардсона,
предлагается определить работу выхода
электрона из чистого металла и по ее
величине указать название метала,
используя справочник.
Исходя из квантовых
представлений, Дешман в 1923 г. получил
для тока насыщения следующую формулу:
![]()
(1)
Где Т
– абсолютная температура катода; К
– постоянная Больцмана; А
– константа, не зависящая от рода
металла.
Формулу (1) можно
записать в виде
![]() ,
,
так как
![]() ,
,
где S
– площадь катода.
Прологарифмируем
это выражение:
![]()
или
![]() ,
,
где
![]()
(2)
Работа выхода
электрона из металла практически не
зависит от температуры, ее можно считать
величиной постоянной, и, следовательно,
![]()
является функцией от 1/Т
. График
зависимости
![]()
представляет прямую линию, угловой
коэффициент которой равен
![]() .
.
Построив график зависимости
![]()
от 1/Т
и определив коэффициент этой прямой,
можно найти работу выхода:
![]()
(3), где![]()
(4)
Рассмотренный
метод называется методом прямых
Ричардсона.
Таблица №1 –
измерение анодного тока Ja
до получения тока насыщения.
|
I1 |
I2 |
I3 |
I4 |
||||
|
JH=1,15 UH=3,0 |
JH=1,2 UH=3,2 |
JH=1,25 UH=3,4 |
JH=1,3 UH=3,7 |
||||
|
Ua, |
Ja, |
Ua, |
Ja, |
Ua, |
Ja, |
Ua, |
Ja, |
|
0 5 10 15 20 25 30 35 40 45 |
0,005 0,282 0,298 0,305 0,310 0,314 0,317 0,320 0,322 0,325 |
0 5 10 15 20 25 30 35 40 45 |
0,008 0,491 0,547 0,560 0,568 0,574 0,579 0,584 0,588 0,592 |
0 5 10 15 20 25 30 35 40 45 |
0,012 0,762 1,025 1,048 1,064 1,076 1,086 1,095 1,102 1,110 |
0 5 10 15 20 25 30 35 40 45 |
0,017 1,118 2,049 2,123 2,159 2,184 2,206 2,223 2,239 2,254 |
Провели измерения
анодного тока Ja
до получения тока насыщения и записали
полученные значения в таблицу №1.
Повторили измерения для нескольких
значений тока накала. Построили на одной
из координатных сетке вольт – амперные
характеристики лампы, используя данные
таблицы №1 для различных токов накала.
Вольт – амперные
характеристики лампы.
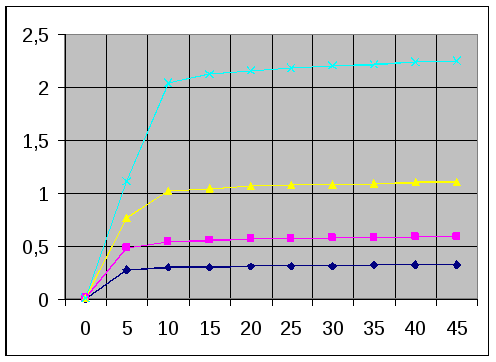
Ua,
B
Ja,
mA
Вычислили по
величине тока и напряжения накала
мощность Р
(Р
= JН
· UН),
потребляемую катодом, разделить ее
величину на площадь катода S=0,05
cм2
и по табличным данным определили
температуру накала, соответствующую
каждому из четырех токов накала. Значение
Р/S,
Т
и токи насыщения записали в таблицу №2.
Таблица №2 –
Значение Р/S,
Т
и токи насыщения.
|
№ |
Р/S·104, |
Т, |
1/Т·10-4, |
1/Т2·10-7, |
Jнас, |
Jнас/Т2·10-7, |
ln(Jнас/Т2) |
|
1 |
82,8 |
2050 |
4,9 |
2,38 |
0,325 |
0,77 |
-16,4 |
|
2 |
93,6 |
2120 |
4,72 |
2,22 |
0,595 |
1,32 |
-15,8 |
|
3 |
102,5 |
2170 |
4,61 |
2,12 |
1,110 |
2,36 |
-15,3 |
|
4 |
117,0 |
2190 |
4,57 |
2,09 |
2,255 |
0,47 |
-16,9 |
Используя данные
таблицы №2, построили два графика: график
зависимости тока насыщения от температуры
накала
![]() ;
;
график зависимости
![]()
График зависимости
тока насыщения от температуры накала
![]()
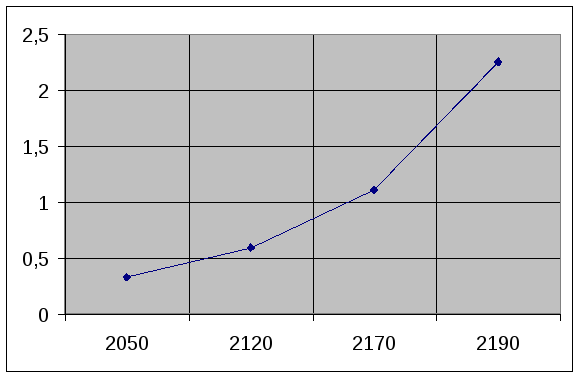
T,
K
Jнас,
мА
График зависимости
![]()
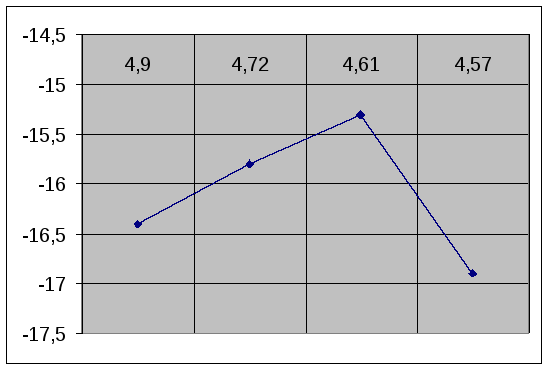
T-1-10-4(K-1)
По графику можно
найти тангенс угла α:
![]()
Теперь можно найти
работу выхода по формуле:
![]()
![]()
По табличными
данными мы получили металл – титан(его
работа выхода, по табличным данным,
равна 3,92).
Вывод:
Изучили
явления термоэлектронной эмиссии и
смогли определить работу выхода электрона
из металла.
Работа выхода
электрона из металла практически не
зависит от температуры, ее можно считать
величиной постоянной, и, следовательно,
![]()
является функцией от 1/Т . График
зависимости
![]()
представляет ломаную, угловой коэффициент
которой равен
![]() .
.
Построив график зависимости
![]()
от 1/Т и определив коэффициент этой
прямой, смогли найти работу выхода(метод
прямых Ричардсона).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1770883 по знаку контактной разности, и изменить ее с помощью делителя напряжения, то можно добиться того, чтобы ток во внешней цепи обратился в нуль. В этом случае приложенное напряжение равно контактной разности, которая, следовательно, определяется непосредственно по показанию вольтметра. Контактная разность потенциалов непосредственно связана с термоэлектронными работами выхода Ф1 и Фг контактирующих тел, а именно; е 012 = Ф1- Ф2, Это соотношение справедливо как для металлов, так и для полупроводников. Поэтому, если работа выхода одного из проводников известна, то, измеряя U>z, можно найти работу выхода другого проводника.
Недостатком этого способа является необходимость усиления измеряемого сигнала, а также наличие механических устройств, предназначенных для реализации данного способа, что является источником погрешности измерения. Для устранения этих недостатков необходимо использование высокочастотных электрических и электроизмерительных устройств. а также прецизионной механики.
Наиболее близким к изобретению по технической сущности является оценочный способ определения работы выхода электрона из материала катода по величине нормального катодного падения потенциала в тлеющем разряда постоянного тока. При изменении тока плотность его остается приблизительно постоянной. Остается постоянным и катодное падение потенциала, До давлений в несколько десятков миллиметров ртутного столба нормальное катодное падение потенциала не зависит от давления газа, а определяется только материалом катода и составом газа. Приближенно нормальное катодное падение пропорционально работе выхода электрона из катода.
Величина катодного падения потенциала лежит в пределах 100-300 В, что используется для устройства газосветных трубок, например неоновых ламп, в которых электродами служат два железных листочка. покрытых слоем бария для уменьшения работы выхода, Недостатком такого спосба является его непригодность для точного измерения работы выхода электрона из-за нелинейного характера распределения потенциала по длине разрядной трубки. По этой причине данные по работам выхода электрона для различных материалов. полученные как оце5
45
40 ночные, в справочной литературе не приводятся.
Цель изобретения — повышение точности измерения работы выхода элек1рона, Поставленная цель достигается тем, что в способе определения работы выхода электрона путем зажигания тлеющего разряда, в качестве эталонного электрода — анода используют твердый электролит, обладающий ионной проводимостью по щелочным металлам, и работу выхода электрона определяют по формуле
А = U/Uý (Аз ЛМе) + AMe, (2) где А — работа выхода исследуемого вещества:
AMe — рабОта ВЫХОда ЩЕЛОЧНОГО МЕтаЛла:
U — потенциал зажигания тлеющего разряда при исследовании вещества с неизвестной работой выхода электрона;
Ue — потенциал зажигания, измеренный предварительно в системе с катодом. работа выхода которого (Аз) принята за второй эталон.
Причинно-следственная связь, позволяющая перейти от поибилизительного соотношения UK.n = С А. где U,п — величина катодного падения потенциала нормального тлеющего разряда: С вЂ” константа, характерная для данного газа; А — неизвестная работа выхода электрона. к предлагаемой формуле состоит в том, что в изобретении используется особый вид разряда, инициируемый и поддерживаемый ионной эмиссией с анода, а не электронной эмиссией с катодов. Явление эмиссии ионов с и”.верхности анода именуется испусканием “=нодных лучей. В данном случае образование анодных лучей состсит в электропереносе ионов натрия сквозь стекло. При этом катодное падение потенциала, имеющее ме то при горении разряда между металлическими катодом и анодом, смещается в толщу стекла, формируя линейное распределение гготенциала по длине разрядной трубки, Данный тип разряда может быть отнесен к линейным явлениям, в которых многие задачи решаются путем составления пропорций, Для составления пропорций производят два опыта; в первом из которых измеряют потенциал зажигания тлеющего разряда Ue между электродами с известными работами выхода:
0э = С(Аэ AMe), (3) а во втором измеряют потенциал зажигания
U между анодом и катодом с неи:.вестной работой выхода:
1770883
U = C(A AMe) (4)
Стационарность.о параметров двух опытов обеспечивается постоянство константы С, исключаемой при почленном делении уравнений (3) и (4), с получением выражения пропорции, которую разрешают относительно неизвестной работы выхода А, т.е. получают формулу (2).
На чертеже приведена схема устройства для осуществления предлагаемого способа.
Устройство содержит анод в виде стакана 1 с расплавом чилийской селитры йаМОз, в которую погружена анодная часть 2 разрядной трубки 3 из стекла С49-1: в состав стекла входит 8,7 мас.% NazO, Так как все стекла, содержащие в своем составе щелочные металлы, обладают ионной проводимостью, для реализации способа можно использовать литиевые. калиевые, цезиевые и другие стекла при замене нитрата натрия на нитрат применяемого в качестве эталона щелочного металла. Торец катодной части 4 разрядной трубки вместе с держателем 5 образца, выполненного из нержавеющей стали, взаимно пришлифованы с целью осуществления разъемного вакуумно-плотного соединения. Исследуемый образец 6, гальванически контактирующий с держателем 5, образует выступающую часть катода в виде механического соединения держателя с образцом для локализации силовых линий поля на его поверхности. Разрядная трубка 3 имеет патрубок 7 для откачки; патрубок 8 предназначен дя напуска рабочего газа. Для определения потенциала зажигания в цепь разрядного контура включен вольтметр 9 с делителем напряжения 10, Для зажигания тлеющего разряда использован высоковольтный источник питания 11.
Работу выхода электрона определяют следующим образом. Исследуемый образец
6 помещают в катодную часть 4 разрядной трубки 3. Через патрубок 7 откачивают газ из разрядной трубки 3. затем через патрубок 8 вводят рабочий газ (аргон или гелий) до давления 0,5-1 Торр. После напуска рабочего газа включают истчоник питания 11, напряжение которого контролируют с rioмощью вольтметра 9. Производят два последовательных определения с помощью вольтметра значений U> и U.
Пример, Измеряют работу выхода вакуумно-плавленой меди. образец которой представляет собой цилиндр диаметром 2 мм и высотой 4 мм. Образец закрепляют на держателе 5 в вертикальном положении
Систему откачивают до дав ения 1 TnDp, Напряжение подают с помощью высоко50
5
40 вольтного источника питания 11 постоянного тока BY-50-50. Потенциал зажигания фиксируют вольтметром 9 марки В-16А, включенным в цепь с помощью делителя напряжения 10. Размеры разрядной трубки при получении данных составляют: длина
400 мм. диаметр 20 мм. толщина стенки стекла С-49 0.5 мм. Для образца потенциал зажигания определяют 10 раз, По данным измерений находят среднее значение потенциала зажигания и ошибку в одно стандартное отклонение. Потенциал зажигания определен равным 4925 B. Для исключения параметров среды в качестве эталона выбран графит. Работа выхода графита принята равной 4.7 эВ. Для определения потенциала зажигания для катода из графита выполняют те же операции, что и для образца меди. Среднее значение потенциала зажигания для него составляет 5525 B. стандартное отклонение среднего — 16 В. В обоих опытах анодом служит образующаяся на внутренней поверхности погруженной в расплав части разрядной трубки пленка натрия, как результат заряда межэлектродной емкости катод — анод. Пленка натрия является вторым эталонным электродом с известной работой выхода. равной 2.35 эВ.
Значение работы выхода вакуумнс-плавленой меди. вычисленное по формуле (2). равно 4,435 +/- 0,065 эВ, Эти же операции проделаны и для других материалов. Значения работ выхода для ряда металлсв. определенные предлагаемым способом. сопоставлены с. рекомендуемыми в таблице.
При удлинении трубки до 600 MM или укорочении до 250 мм при давлении рабочего газа в интервале 1-5 Торр данные табл цы воспроизводятся. так как эти вариации, изменяя значения потенциалов зажигания. не влияют на величину их отношения. т.е. U /U> сохраняется постоянным. равным 4925 B/
/5525 B = 0,887.
Из данных таблицы видно. что в пределах ошибки в два с андартных отклонения результаты исследования совпадак т с рекомендуемыми значениями.
Таким образом, предлагаемый способ обладает высокой степенью достоверности. обеспечиваемой T|. M что в способе использован электролизный закон Фарадея. относящийся к одному из фундамен альных законов природы.
Формула изобретения
Способ определения работы выхода электрона путем зажигания тлеющего разряда в среде инертного газа при пониженном давлении между электродами газоразрядной стеклянной тоубки. о т л и— ч а ю шийся тем. что. с целью повышения
1770883 (эВ), реко д точности измерения работы выхода электрона, в качестве эталонного электрода-анода используют твердый электролит, обладающий ионной проводимостью по щелочным металлам, и работу выхода электрона определяют по потенциалу зажигания тлеющего разряда по формуле
A = И0э (Аэ АМе) + АМе, где А — работа выхода исследуемого вещества:
AMe — работа выхода щелочно о металла:
U — потенциал зажигания тлеющего разряда, при исследовании вещества с
5 неизвестной работой выхода электрона:
U> — потенциал зажигания, измеренный в системе с катодом. работа выхода которого (Аэ) принята за второй эталон.




Содержание
- Работа выхода электронов из металлов, не металлов и неорганических соединений (Таблица)
- Формула работа выхода электронов
- Таблица работа выхода электронов из простых веществ
- Таблица значений работы выхода электронов из простых веществ. Формулы.
- Таблица значений работы выхода электронов из простых веществ. Формулы.
- Таблица значений работы выхода электронов из простых веществ.
- Работа выхода электронов из металла. Контактные явления
- 1. Работа выхода электронов из металла.
- 2. Термоэлектронная эмиссия.
- 3. Контактная разность потенциалов.
- 4. Закон Вольта.
- 5. Термо-ЭДС.
- 6. Эффект Пельтье,1834 г.
- 7. Эффект Томсона.
Формула работа выхода электронов
В металлах имеются электроны проводимости, образующие электронный газ и участвующие в тепловом движении. Так как электроны проводимости удерживаются внутри металла, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. Эта работа, естественно, различна для разных металлов.
Потенциальная энергия электрона внутри металла постоянна и равна:
Wp = -eφ , где j – потенциал электрического поля внутри металла.
При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. Распределение энергии электрона внутри металла можно представить в виде потенциальной ямы.
В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы, т.е.
Этот результат соответствует классической электронной теории металлов, в которой предполагается, что скорость электронов в металле подчиняется закону распределения Максвелла и при температуре абсолютного нуля равна нулю. Однако в действительности электроны проводимости подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и соответственно их энергия отлична от нуля.
Максимальное значение энергии, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . Квантовая теория проводимости металлов, основанная на этой статистике, дает иную трактовку работы выхода. Работа выхода электрона из металла равна разности высоты потенциального барьера eφ и энергии Ферми.
где φ’ – среднее значение потенциала электрического поля внутри металла.
Таблица работа выхода электронов из простых веществ
В таблице приведены значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки.
Источник
Таблица значений работы выхода электронов из простых веществ. Формулы.
Таблица значений работы выхода электронов из простых веществ. Формулы.
Так как электроны вообще-то удерживаются внутри веществ, то, следовательно, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона.
- Упрощенная теория выхода электронов: Потенциальная энергия электрона внутри металла постоянна и равна:
- Wp = -e*φ, где φ потенциал электрического поля внутри металла.
- При переходе электрона через поверхностный электронный слой потенциальная энергия быстро уменьшается на величину работы выхода и становится вне металла равной нулю. В рассмотренной выше трактовке работа выхода электрона равна глубине потенциальной ямы (энергии внутри металла), т.е.:
- Aвых = e*φ
- Более строгая теория основана на том, что: электроны проводимости (те, что вообще могут выйти) подчиняются квантовой статистике Ферми-Дирака, согласно которой при абсолютном нуле скорость электронов и их энергия отлична от нуля. Энергия, которой обладают электроны при абсолютном нуле, называется энергией Ферми EF . В этом случае: работа выхода электрона из металла равна разности высоты потенциального барьера (e*φ ) и энергии Ферми:
- Aвых = e φ’ — EF , где φ’ – среднее значение потенциала электрического поля внутри металла. ;
Таблица значений работы выхода электронов из простых веществ.
В таблице приведены «идеальные» значения работы выхода электронов, относящихся к поликристаллическим образцам, поверхность которых очищена в вакууме прокаливанием или механической обработкой. Недостаточно надежные данные заключены в скобки. При этом чледует понимать, что необработанная поверхность может и увеличивать и уменьшать эту ыеличину. Порядок то уж точно сохранится 🙂
Источник



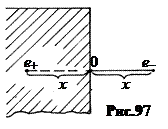
1. Работа выхода электронов из металла.
Электроны проводимости в кристалле находятся в потенциальной яме. Выход из нее требует совершения работы по преодолению силы, действующей на электрон со стороны кристалла. Найдем эту силу. Обладая энергией теплового движения, электроны могут выскакивать из кристалла на расстояние в несколько периодов. Вышедший из кристалла и находящийся у его поверхности на расстоянии х электрон индуцирует в металле заряд е+ (рис.97). Этот наведенный заряд действует на вышедший электрон так, как если бы он был сосредоточен под поверхностью металла на глубине х в точке, симметричной той, в которой находится электрон (см. Эл-во §5). Индуцированный заряд е+ называется электрическим изображением заряда е—. Оба точечные заряда притягиваются друг к другу с силой Кулона 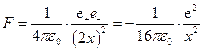 . (14.1)
. (14.1)
Но это и есть сила притяжения металлом вышедшего из него электрона. Под действием этой силы электрон втягивается обратно в металл. Чтобы удалить электрон из металла, надо совершить работу по преодолению этой силы, перемещая электроны на бесконечность из точки, расположенной на расстоянии х от поверхности металла. В качестве х можно взять межатомное расстояние.
На рис.98 показана зависимость потенциальной энергии электрона от расстояния х до атомной плоскости – стенки металла. Энергетическое расстояние еj от уровня Ферми до нулевого уровня называют термодинамической работой выхода электрона, величину j – потенциалом выхода. Уровень Ес обозначает дно зоны проводимости, где Е = 0. У металлов работа выхода еj заключена в пределах 1,8 ¸ 5,3 эВ. Меньше всего она у щелочных металлов, больше – у золота, серебра, платины (табл. 14.1).
| Таблица 14.1 | |||
| Металл | еj, эВ | Металл | еj, эВ |
| Литий Li | 2,38 | Платина Pt | 5,32 |
| Натрий Na | 2,35 | Ванадий V | 4,58 |
| Калий К | 2,22 | Вольфрам W | 4,54 |
| Рубидий Rb | 2,16 | Золото Au | 4,30 |
| Цезий Cs | 1,18 | Серебро Ag | 4,30 |

Большое влияние на работу выхода оказывают мономолекулярные адсорбированные слои. Например, слой атомов цезия Cs на вольфраме W (рис.99). Цезий щелочной металл. Его внешний, валентный электрон связан с ядром значительно слабее, чем валентные электроны в вольфраме. Поэтому атомы цезия отдают вольфраму свои валентные электроны и превращаются в положительные ионы. Между этими ионами и их электрическими изображениями в вольфраме возникает сила притяжения, удерживающая ионы цезия на поверхности вольфрама. Поле этого двойного электрического слоя помогает выходу электронов из вольфрама. По этому в присутствии слоя цезия работа выхода электрона из вольфрама уменьшается с 4,54 эВ до 1,38 эВ. Подобно цезию действуют одноатомные слои бария Ba, церия Cе, тория Th и др.
2. Термоэлектронная эмиссия.
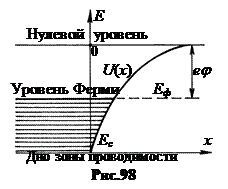
С повышением температуры металла поверхность Ферми разрыхляется, энергия электронов увеличивается, и они поднимаются на более высокие уровни (рис.100). Соответственно уменьшается работа выхода электронов. Поэтому концентрация вылетевших из кристалла электронов в пристеночном слое растет. Процесс испускания электронов нагретым металлом называется термоэлектронной эмиссией.
Формально термоэлектронная эмиссия есть всегда, когда Т > 0 К. Но заметной она становится при температурах Т > 800 К.
Облако термоэлектронов находится в динамическом равновесии. Число вылетевших из металла электронов в каждый промежуток времени примерно равно числу электронов, втянутых в металл. Поэтому суммарный ток эмиссии равен нулю.

На основе термоэлектронной эмиссии построен ламповый вакуумный диод (рис.101). Здесь К – катод, обычно нагреваемая вольфрамовая спираль, А – анод, холодная металлическая пластина обычно цилиндрической формы. По оси этого цилиндра натягивается спираль катода. Оба электрода помещаются в стеклянный сосуд с высоким вакуумом.
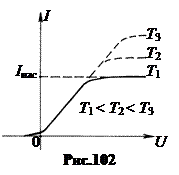
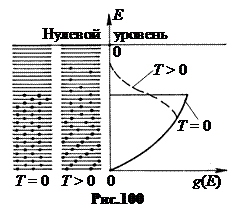
Если между катодом и анодом создавать электрическое поле с напряжением U, как показано на рис.101, то термоэлектроны под действием этого поля будут перемещаться от катода к аноду. Возникает электрический ток в вакууме. Вольтамперная характеристика вакуумного диода показана на рис.102. С повышением анодного напряжения U ток I через анод растет почти пропорционально U. Но при достижении некоторого значенья Iнас перестает увеличиваться. Это предельное значение Iнас называют ток насыщением. Он возникает тогда, когда все электроны, вылетевшие из нагретого катода, захватываются полем и переносятся к аноду.

С повышением температуры катода ток насыщения увеличивается. Разделив ток насыщения на поверхность S катода, получаем плотность тока насыщения jнас = iнасçS. В 1901г. Оуэн Ричардсон, исходя из классических представлений, теоретически нашел зависимость плотности тока насыщения от температуры поверхности катода. Уточненная Дешманом в 1923г. с учетом квантовых представлений, зависимость jнас(Т) имеет вид: 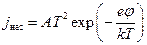 . Формула Ричардсона-Дэшмана (14.2)
. Формула Ричардсона-Дэшмана (14.2)
Здесь еj – работа выхода, А – константа, имеющая разное значение у разных металлов и колеблющаяся около теоретического значения А= 1,2·10 6 Аç(м 2 К 2 ).
3. Контактная разность потенциалов.
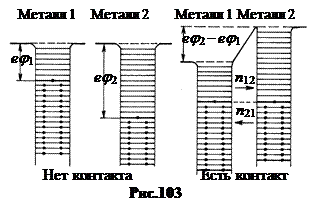
Рассмотрим процессы, происходящие при контакте двух разных металлов. Допустим, до электрического контакта металл 1 (на рис.103 слева) имеет работу выхода еj1, а работа выхода металла 2 больше, j2 > j1.
Приведем металлы в состояние электрического контакта, то есть сблизим их до такого расстояния, при котором возможен эффективный обмен электронами. Поскольку работа выхода электронов из металла 2 больше, то уровень Ферми в металле 2 ниже, чем в металле 1. В результате электроны проводимости с уровня Ферми металла 1 начинают переходить на уровень Ферми металла 2.
В результате такого перехода электронов металл 2 заряжается отрицательно, энергия электронов и, соответственно, уровень Ферми в нем повышаются. Металл 1 заряжается положительно, энергия электронов и уровень Ферми в нем понижаются. Между металлами возникает контактная разность потенциалов j12.
Суммарное перетекание зарядов прекратится, когда уровни Ферми сравняются, а разность потенциалов между проводниками будет равна разности потенциалов выхода, j12 = j2 — j1, и встречные потоки электронов сравняются n21=-n12 (рис.103 справа). Контактная разность потенциалов между проводниками создает для электронов, переходящих в проводник с большей работой выхода, потенциальный барьер высотой еj12.
Оценим количество электронов, перетекающих из одного металла в другой при возникновении контактной разности потенциалов j12. Будем считать, что между контактирующими металлами остается зазор шириной d, а заряды концентрируются на контактирующих поверхностях. Тогда заряд Q на каждой из поверхностей, необходимый для создания напряжения j12, найдется из формулы плоского конденсатора, 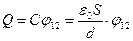 . (14.3)
. (14.3)
Как видно из таблицы 14.1, контактная разность потенциалов 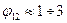 В. Расстояние d между металлами не может быть меньше параметра решетки а » 0,3 нм. Полагая j12 =1 В и d = 0,3 нм, получаем максимальную плотность заряда на контактирующих поверхностях.
В. Расстояние d между металлами не может быть меньше параметра решетки а » 0,3 нм. Полагая j12 =1 В и d = 0,3 нм, получаем максимальную плотность заряда на контактирующих поверхностях.
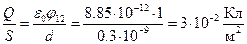 .
.
Разделив на заряд электрона получаем, что на 1 м 2 поверхности приходится 2·10 17 электронов. Если диаметр атомов взять равным постоянной решетки а = 0,3 нм, то на 1 м 2 поверхности в одноатомном слое металла размещается 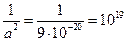 атомов. Если атомы металла содержат по одному валентному электрону, то для создания контактной разности потенциалов 1 В потребовалось всего лишь (2×10 17 ç10 19 )´100% = 2% электронов проводимости одноатомного поверхностного слоя.
атомов. Если атомы металла содержат по одному валентному электрону, то для создания контактной разности потенциалов 1 В потребовалось всего лишь (2×10 17 ç10 19 )´100% = 2% электронов проводимости одноатомного поверхностного слоя.
4. Закон Вольта.
Контактную разность потенциалов открыл в девяностых годах XVIII века итальянец Александр Вольта. В серии экспериментов 1792–1794 годов он установил, что в цепочке из ряда последовательно соединенных металлов контактная разность потенциалов зависит лишь от крайних металлов. Этот опытный факт называется законом Вольта. Действительно, пусть имеется цепочка из металлов 1,2,3,4 (рис.104). Работа выхода металлов еj1, еj2, еj3, еj4. На границе каждой пары возникает контактная разность:
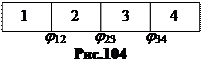
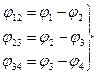 (14.4)
(14.4)
Просуммировав левые и правые части, получаем: 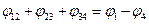 . (14.5)
. (14.5)
Сумма всех контактных ЭДС (левой части равенства) равна контактной ЭДС крайних металлов в цепочке (правая часть равенства). Если концы цепи замкнуть, то независимо от количества звенев сумма контактных разностей потенциалов равна нулю. Тока в цепи нет.
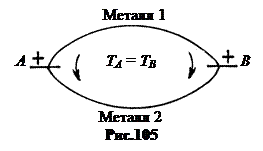
5. Термо-ЭДС.
Сумма контактных разностей потенциалов в замкнутой цепи равна нулю лишь при условии, что температуры всех контактов одинаковы. В 1821 г. Томас Зеебек, сжимая концы висмутовой и медной пластинок теплыми пальцами обнаружил, что если цепь замкнута, то в ней протекает ток. Это явление возникновения ЭДС в цепи из разных металлов при перепаде температур между спаями называют эффектом Зеебека или термоэлектричеством. В рамках классической электронной теории можно дать простое толкование явлению Зеебека и получить зависимость термо-ЭДС от перепада температур.
Пусть имеется замкнутая цепь из двух металлов 1 и 2 со спаями A и B (рис.105). Полагаем, что электроны проводимости на верхних уровнях зоны проводимости распределяются в силовом поле решетки по закону Больцмана.
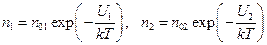 (14.6), (14.7)
(14.6), (14.7)
Здесь n01 и n02 – концентрация электронов проводимости на уровнях Ферми. В силу полной заполняемости этих уровней будем полагать n01 = n02; U1 и U2 – потенциальная энергия электронов в металлах 1 и 2. Она может изменяться от нуля на уровне Ферми до еj (работа выхода) на нулевом уровне. Разделим первое уравнение на второе.
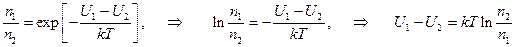 . (14.8)
. (14.8)
Разделив разность U1 –U2 на заряд электрона е, получаем концентрационную разность потенциалов между металлами 1 и 2. 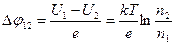 . (14.9)
. (14.9)

Если температуры спаев ТА и ТB одинаковы, то концентрационная ЭДС в замкнутой цепи, так же, как контактная разность потенциалов, равна нулю. Тока в цепи нет. Если же температуры спаев разные, ТА ¹ ТB, то в цепи возникает термо-ЭДС (рис.106). Концентрационные перепады потенциалов в контактах А и B разные.
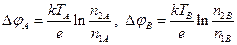 . (14.10)
. (14.10)
Концентрация свободных электронов слабо зависит от температуры. Поэтому можно полагать, что n1A = n1В= n1, n2A = n2В = n2. ЭДС, возникающая в цепи, равна 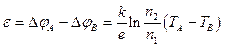 . (14.11)
. (14.11)
| Таблица 14.2 | |
| Пара | а, 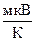 |
| Висмут – Платина | –65,0 |
| Железо – Платина | +16,0 |
| Медь – Платина | +7,4 |
| Никель – Платина | –16,4 |
| Сурьма – Платина | +47,0 |
| Константан – Платина | –34,4 |
Учитывая грубость классических приближений, обычно выделяют лишь температурную зависимость, которая хорошо подтверждается опытом при малых перепадах температур, 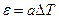 . (14.12)
. (14.12)
Коэффициент а называют дифференциальной термо-ЭДС пары металлов. В таблице 14.2 приведены значения а для наиболее употребительных металлов в паре с платиной. Чтобы определить величину а пары металлов без платины, надо найти разность значений а в таблице. Например, для пары Bi – Sb, а = -65,0 — 47,0 = -112,0 мкВçК. Для пары медь – константан а = +7,4 — (-34,4) = 48,8 мкВçК.
Термо-ЭДС, возникающая в цепи из разных металлов, широко применяется для измерения температур в диапазоне от 0 К до » 1000°С. Соответствующее устройство из двух разных металлов называется термопарой. Один спай термопары поддерживается при постоянной температуре, например при 0 о С в сосуде с тающим льдом, другой помещают в ту среду, температуру которой хотят измерить. О величине температуры можно судить как по величине термотока, измеряемого гальванометром, так и более точно по величине термо-ЭДС, измеряемой методом компенсации. С помощью термопар можно измерять температуру с точностью до сотых долей градуса.
6. Эффект Пельтье,1834 г.
Он обратен эффекту Зеебека и состоит в том, что при пропускании тока по цепи из разных металлов один контакт у металла нагревается, другой охлаждается.
Пусть в цепи из двух разных металлов действует источник тока – батарея Б. В результате в цепи идет постоянный ток I (рис.107). Проходя спай B, электроны, идущие по цепи на рисунке против часовой стрелки, дополнительно ускоряются полем контактного потенциала. Их скорость дрейфа увеличивается, поэтому при столкновении с узлами электроны передают им большую, по сравнению со средней, энергию. Спай В нагревается больше, чем рядом расположенные участки проводников.
В спае А электроны тормозятся контактным полем, их скорость дрейфа уменьшается, поэтому спай А нагревается меньше, чем рядом расположенные участки проводов. Кроме того, для установления равновесия этих электронов с электронным газом им необходимо приобрести еще энергию. Эту энергию они черпают из решетки. В результате спай А охлаждается больше, чем нагревается. В итоге теплота в спае А поглощается.
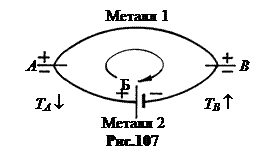
Выделяющаяся или поглощающаяся теплота Пельтье QП в контакте пропорциональна заряду It, прошедшему через контакт. 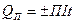 . (14.13)
. (14.13)
Здесь П – коэффициент Пельтье связан с дифференциальной термо-ЭДС соотношением: П = аDT.(14.14)
Где DТ – разность температур между контактами.
Эффект Пельтье позволяет создавать малогабаритные холодильные устройства. Их особенность в том, что изменяя направление тока в цепи, можно один и тот же контакт заставить как поглощать тепло (холодильник), так и выделять его (нагреватель).
7. Эффект Томсона.
В 1853 – 54 г.г. Рудольф Клаузиус и Уильям Томсон независимо друг от друга применили к явлениям термоэлектричества принципы термодинамики. В процессе построения термодинамической теории термоэлектричества Томсон установил, что неравномерно нагретый проводник должен вести себя как система находящихся в контакте физически разнородных участков. На этом основании Томсон пришёл к заключению и подтвердил его экспериментально, что в однородном неравномерно нагретом проводнике должно выделяться или поглощаться тепло Пельтье (тепло Томсона). Само явление назвали эффектом Томсона.
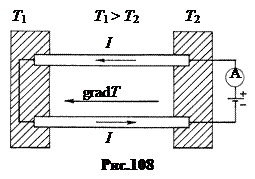
Принципиальная схема экспериментальной установки изображена на рис.108
Концы двух одинаковых проводящих стержней помещены в два термостата с разными температурами Т1 и Т2. Допустим, Т1 > Т2. Тогда градиент температуры в верхнем стержне направлен по току I, а в нижнем – против тока. В результате в одном стержне выделяется тепло Томсона (его температура выше), а в другом – поглощается.
Знак эффекта у разных проводников разный. В висмуте и цинке, например, тепло выделяется, если поток тепла и электрический ток совпадают по направлению (на рисунке нижний проводник). А в Fe, Pt, Sb при тех же условиях тепло поглощается. С изменением направления тока знак эффекта во всех проводниках меняется.
Тепло Томсона Q, выделяющееся в проводнике, пропорционально перепаду температур ΔТ, току I, протекающему по проводнику, и времени t Q = σΔTIt.
Здесь σ – коэффициент Томсона. Он зависит от материала провода и от его температуры. Коэффициент σ невелик. У металлов он порядка 10 –5 ВçК. За положительное направление тока принимают направление градиента температур, то есть направление от холодного конца проводника к горячему. Если тепло при этих условиях выделяется (проводник нагревается), эффект Томсона считается положительным.
Количественно эффект Томсона исследовал в 1867 г. Франсуа Леру. В установке, собранной по схеме рис. 108, к поверхности стержней он присоединял спаи термопар. Пока тока через стержни не было, термоЭДС в цепи термопар была равна нулю. При включении тока через стержни появлялась термоЭДС, величина и знак которой позволяли определить коэффициент Томсона σ.
8. Закон Джоуля – Ленца в замкнутой цепи всегда выполняется. Суммарный эффект Пельтье и Томсона в замкнутой цепи равен нулю, поскольку наряду с участками цепи, где тепло Пельтье и Томсона выделяется, всегда есть участки, где такое же тепло поглощается.
Источник
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.

Александр Столетов
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
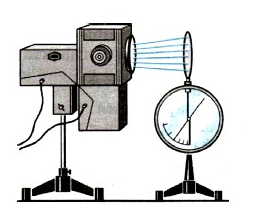
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
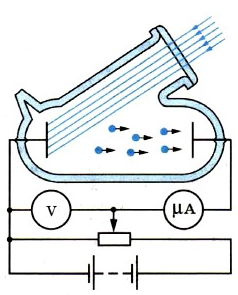
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
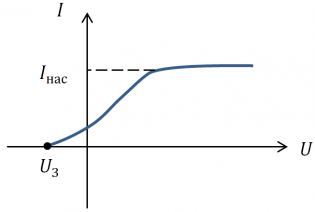
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как Iн. Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
Iн=qt
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
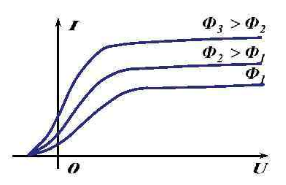
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное Uз, сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное Uз, называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
mv22=eUз
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
E=hν
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10–34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10–7 м.
Энергия фотона равна:
E=hν
Выразим частоту фотона через скорость света:
ν=cλ
Следовательно:
![]()
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
hν=A+mv22
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
hν>A
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
νmin=Ah
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
λmax=hcA
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10-7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10–19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
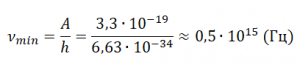
Задание EF15717
При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅1015 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Переписать формулу закона сохранения энергии применительно к опытам 1 и 2.
4.Используя формула, связывающую задерживающее напряжение и кинетическую энергию фотона, определить работу выхода.
5.Записать формулу для красной границы фотоэффекта.
6.Выполнить решение в общем виде.
7.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Частота света в опыте 1: ν1 = ν = 0,75∙1015 Гц.
• Частота света в опыте 2: ν2 = 2ν1 = 2ν Гц.
• Задерживающее напряжение в опыте 1: U1 = U В.
• Задерживающее напряжение в опыте 2: U2 = 3U1 = 3U В.
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
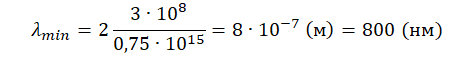
Ответ: 800
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17645
При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался красный светофильтр, а во второй – жёлтый. В каждом опыте измеряли напряжение запирания.
Как изменяются длина световой волны, напряжение запирания и кинетическая энергия фотоэлектронов? Для каждой величины определите соответствующий характер её изменения:
| 1) | увеличится |
| 2) | уменьшится |
| 3) | не изменится |
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.

Алгоритм решения
1.Определить, от чего зависит и как меняется длина световой волны.
2.Записать закон сохранения энергии, формулу зависимости кинетической энергии от напряжения запирания.
3.Используя формулы, становить, как меняется напряжение запирания и кинетическая энергия.
Решение
Длина световой волны определяется ее цветом. Красный свет имеет большую длину волны. Следовательно, во втором опыте длина световой волны уменьшится.
Закон сохранения энергии для фотоэффекта:
hν=A+mv22
Формула зависимости кинетической энергии от напряжения запирания:
mv22=eUз
Следовательно:
hν=A+eUз
Работы выхода — величина постоянная для данного вещества. Следовательно, напряжение запирания зависит только от частоты световой волны. Частота — величина обратная длине волны. Так как длина волны уменьшилась, частота увеличилась. Следовательно, увеличилось и напряжение запирания.
Поскольку напряжение запирания прямо пропорционально кинетической энергии фотонов, то эта энергия также увеличивается.
Ответ: 211
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17973
На металлическую пластинку падает монохроматическая электромагнитная волна, выбивающая электроны из пластинки. Максимальная кинетическая энергия фотоэлектронов, вылетевших из пластинки в результате фотоэффекта, составляет 3 эВ, а работа выхода из металла в 2 раза больше этой энергии. Чему равна энергия фотонов в падающей волне?
Ответ:
а) 9 эВ
б) 2 эВ
в) 3 эВ
г) 6 эВ
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Максимальная кинетическая энергия выбитых электронов: Emax = 3 эВ.
• Работа выхода из металла: A = 2 Emax.
Закона сохранения энергии для фотоэффекта:
hν=A+mv22
Или:
E=A+Emax=2Emax+Emax=3Emax=3·3=9 (эВ)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.3k




