Как можно найти ранг матрицы

Перед тем как начать знакомство с темой, необходимо повторить правила нахождения определителей второго, третьего и высших порядков. Также необходимо знать, что детерминант 1-го порядка — число. Рассмотрим 2 метода вычисления ранга матриц.

Онлайн-калькулятор

Метод окаймляющих миноров

Для нахождения ранга матрицы данным методом требуется уметь находить миноры матриц.

Ранг матрицы

Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 00.

При этом ранг матрицы не может превышать порядка матрицы: 0⩽rang Qm×n⩽min(m,n)0leqslant rang Q_{mtimes n}leqslant min (m, n).

Обозначить ранг матрицы QQ можно следующим образом: rang Qrang Q или r(Q)r(Q).

Если ранг матрицы QQ равен rr, то это означает, что в матрице QQ имеется отличный от нуля минор порядка rr. При этом всякий минор порядка больше, чем rr равен нулю.

Исходя из определения ранга матрицы, следует, что если все миноры первого порядка (т. е. элементы матрицы QQ) равны 00, то rang Q=0rang Q=0. Если один из миноров первого порядка отличен от 00, а все миноры второго порядка равны 00, то rang Q=1rang Q=1. Если все миноры kk-го порядка равны 00, или миноров kk-го порядка не существует, то rang Q=k−1rang Q=k-1.

Рассмотрим примеры нахождения ранга матриц данным методом.

Пример 1

Найти ранг матрицы методом окаймляющих миноров

F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.

Данная матрица имеет размер 3×33times3, поэтому ее ранг не может быть больше 33, т.е. rang F⩽3rang Fleqslant3.

Перейдем к вычислению ранга матрицы.

Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang F≥1rang Fgeq1.

Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣0321∣=0⋅1−2⋅3=0−6=−6begin{vmatrix}0&3\2&1end{vmatrix}=0cdot1-2cdot3=0-6=-6. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang F≥2rang Fgeq2.

Перейдем к проверке миноров 3-го порядка. Минор 3-го порядка — определитель матрицы FF, поскольку она состоит из 3 строк и 3 столбцов: ∣03−1210−2−10∣=0begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0. Значит, ранг матрицы FF равен 22, или rang F=2rang F=2.

Пример 2

Найти ранг матрицы методом окаймляющих миноров

K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.

Данная матрица имеет размер 5×45times4. Из чисел 55 и 44 минимальным является 44, поэтому ее ранг не может быть больше 44, а значит rang K⩽4rang Kleqslant4.

Перейдем к вычислению ранга матрицы.

Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang K≥1rang Kgeq1.

Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣21−12∣=2⋅2−(−1)⋅1=4+1=5begin{vmatrix}2&1\-1&2end{vmatrix}=2cdot2-(-1)cdot1=4+1=5. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥2rang Kgeq2.

Перейдем к проверке миноров 3-го порядка. Например, на пересечении строк №1, №3 и №5 и столбцов №2, №3 и №4 получим минор:

∣1−233−153−31∣=1⋅(−1)⋅1+(−2)⋅5⋅3+3⋅(−3)⋅3−3⋅(−1)⋅3−(−2)⋅1⋅3−1⋅5⋅(−3)=−1−30−27+9+6+15=−28begin{vmatrix}1&-2&3\3&-1&5\3&-3&1end{vmatrix}=1cdot(-1)cdot1+(-2)cdot5cdot3+3cdot(-3)cdot3-3cdot(-1)cdot3-(-2)cdot1cdot3-1cdot5cdot(-3)=-1-30-27+9+6+15=-28.

Значит, среди миноров 3-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥3rang Kgeq3.

Перейдем к проверке миноров 4-го порядка. Например, на пересечении строк №1, №2, №3 и №4 и столбцов №1, №2, №3 и №4 получим минор:

∣21−23−121213−15−2−212∣=2(−1)1+1∣2123−15−212∣−(−1)2+1∣1−233−15−212∣+(−1)3+1∣1−23212−212∣−2(−1)4+1∣1−232123−15∣=2(−1)2∣2123−15−212∣−(−1)3∣1−233−15−212∣+(−1)4∣1−23212−212∣−2(−1)5∣1−232123−15∣=2∣2123−15−212∣+∣1−233−15−212∣+∣1−23212−212∣+2∣1−232123−15∣=2(−4+6−10−4−10−6)−2+9+20−6−5+12+2+6+8+6−2+8+2(5−6−12−9+2+20)=−56+56+0=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2end{vmatrix}=2(-1)^{1+1}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{2+1}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{3+1}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{4+1}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-1)^{2}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{3}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{4}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{5}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}+2begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-4+6-10-4-10-6)-2+9+20-6-5+12+2+6+8+6-2+8+2(5-6-12-9+2+20)=-56+56+0=0.

Остальные миноры 4-го порядка также равны нулю:
∣21−23−121213−1543−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}=0,

∣21−23−1212−2−21243−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,

∣21−2313−15−2−21243−31∣=0begin{vmatrix}2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,

∣−121213−15−2−21243−31∣=0begin{vmatrix}-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0.

Значит, ранг матрицы KK равен 33, или rang K=3rang K=3.

Данный метод не всегда удобен, поскольку связан с вычислением большого количества определителей. Рассмотрим метод нахождения ранга матриц, который наиболее часто применяется на практике.

Метод Гаусса (метод элементарных преобразований)

Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:

1. перестановка местами любых двух рядов (строк или столбцов) матрицы;
2. умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
3. прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.

Ранг матрицы

Рангом матрицы называется количество ненулевых строк матрицы после ее приведения к ступенчатому виду при помощи элементарных преобразований над строками и столбцами.

Рассмотрим суть данного метода на примерах.

Пример 1

Найти ранг матрицы методом Гаусса F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.

Приведем матрицу FF с помощью элементарных преобразований к ступенчатому виду.

Поменяем местами строки №1 и №2:

(03−1210−2−10)∼(21003−1−2−10)begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}sim begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}.

Прибавим к строке №3 строку №1, умноженную на 1:

(21003−1−2−10)∼(21003−1000)begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}simbegin{pmatrix}2&1&0\0&3&-1\0&0&0end{pmatrix}.

С помощью элементарных преобразований мы привели матрицу FF к ступенчатому виду. В ней остались 2 ненулевые строки, следовательно, rang F=2rang F=2.

Пример 2

Найти ранг матрицы методом Гаусса

K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.

Приведем матрицу KK с помощью элементарных преобразований к ступенчатому виду.

Поменяем местами строки №1 и №2:

(21−23−121213−15−2−21243−31)∼(−121221−2313−15−2−21243−31)begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.

Поменяем местами строки №2 и №4:

(−121221−2313−15−2−21243−31)∼(−1212−2−21213−1521−2343−31)begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}.

Поменяем местами строки №3 и №4:

(−1212−2−21213−1521−2343−31)∼(−1212−2−21221−2313−1543−31)begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}.

Поменяем местами строки №4 и №5:

(−1212−2−21221−2313−1543−31)∼(−1212−2−21221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -2:

(−1212−2−21221−2343−3113−15)∼(−12120−6−1−221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.

Прибавим к строке №3 строку №1, умноженную на 2:

(−12120−6−1−221−2343−3113−15)∼(−12120−6−1−2050743−3113−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}.

Прибавим к строке №4 строку №1, умноженную на 4:

(−12120−6−1−2050743−3113−15)∼(−12120−6−1−205070111913−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}.

Прибавим к строке №5 строку №1, умноженную на 1:

(−12120−6−1−205070111913−15)∼(−12120−6−1−20507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.

Прибавим к строке №2 строку №3, умноженную на 1:

(−12120−6−1−20507011190507)∼(−12120−1−150507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.

Прибавим к строке №5 строку №3, умноженную на -1:

(−12120−1−150507011190507)∼(−12120−1−150507011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}.

Прибавим к строке №3 строку №2, умноженную на 5:

(−12120−1−150507011190000)∼(−12120−1−1500−532011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}.

Прибавим к строке №4 строку №2, умноженную на 11:

(−12120−1−1500−532011190000)∼(−12120−1−1500−53200−10640000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}.

Прибавим к строке №4 строку №3, умноженную на -2:

(−12120−1−1500−53200−10640000)∼(−12120−1−1500−53200000000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&0&0\0&0&0&0end{pmatrix}.

С помощью элементарных преобразований мы привели матрицу KK к ступенчатому виду. В ней остались 3 ненулевые строки, следовательно, rang K=3rang K=3.

Любым из рассмотренных методов можно найти ранг матрицы.

Наши эксперты готовы оказать вам помощь с решением задачи онлайн по самым низким ценам!

Тест по теме «Ранг матрицы»

В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.

Минор матрицы

Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.

Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.

Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.

При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2

Другим минором 2-го порядка матрицы А является 0011=0

Предоставим иллюстрации построения миноров второго порядка матрицы А:

Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:

003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9

Иллюстрация, как получается минор 3-го порядка матрицы А:

Для данной матрицы миноров выше 3-го порядка не существует, потому что

k≤min(p, n)=min (3, 4)=3

Сколько существует миноров k-ого порядка для матрицы А порядка p×n?

Число миноров вычисляют по следующей формуле:

Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.

После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.

Ранг матрицы: методы нахождения

Ранг матрицы — наивысший порядок матрицы, отличный от нуля.

Rank (A), Rg (A), Rang (A).

Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.

Нахождение ранга матрицы по определению

Метод перебора миноров — метод, основанный на определении ранга матрицы.

Алгоритм действий способом перебора миноров:

Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).

Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.

Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.

Нахождение ранга матрицы методом окаймляющих миноров

Проще говоря, матрица, которая соответствует окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору Mok , вычеркиванием элементов одной строки и одного столбца.

Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.

Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.

Алгоритм действий:

Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.

Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.

Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.

Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)

Вспомним, что представляют собой элементарные преобразования.

Элементарные преобразования:

• путем перестановки строк (столбцов) матрицы;
• путем умножение всех элементов любой строки (столбца) матрицы на произвольное ненулевое число k;

путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.

Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).

Справедливость данного утверждения следует из определения матрицы:

• в случае перестановки строк или столбцов матрицы ее определитель меняет знак. Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю;
• в случае умножения всех элементов какой-либо строки (столбца) матрицы на произвольное число k, которое не равняется нулю, определитель полученной матрицы равен определителю исходной матрицы, которая умножена на k;

в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.

Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.

Для чего?

Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.

Проиллюстрируем этот процесс:

• для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов:

А~1b12b13⋯b1n-1b1n01b23⋯b2n-2b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01000⋯00⋮⋮⋮⋮⋮⋮000⋯00, Rank(A)=n

или

А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k

• для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов:

А~1b12b13⋯b1pb1p+1⋯b1n01b23⋯b2pb2p+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bpp+1⋯bpn, Rank(A)=p

или

А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0

• для квадратных матриц А порядка n на n:

А~1b12b13⋯b1n-1b1n01b23⋯b2n-1b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01, Rank(A)=n

или

A~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k, k<n

Если проводить элементарные преобразования, то не допускаются приближенные значения!

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 сентября 2022 года; проверки требуют 7 правок.

Рангом системы строк (столбцов) матрицы с строками и столбцами называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков всевозможных ненулевых миноров этой матрицы. Ранг нулевой матрицы любого размера равен нулю. Если все миноры второго порядка равны нулю, то ранг равен единице, и т.д.

Ранг матрицы — размерность образа линейного оператора, которому соответствует матрица.

Обычно ранг матрицы обозначается , , , или . Последний вариант свойственен для английского языка, в то время как первые два — для немецкого, французского и ряда других языков.

Определение[править | править код]

Пусть  — прямоугольная матрица.

Тогда по определению рангом матрицы является:

Связанные определения[править | править код]

Свойства[править | править код]

Теорема (о базисном миноре): Пусть  — базисный минор матрицы , тогда:

• базисные строки и базисные столбцы линейно независимы;
• любая строка (столбец) матрицы есть линейная комбинация базисных строк (столбцов).

Следствия:

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны.

Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:

• Количество главных переменных системы равно рангу системы.
• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Ранг of A равен r тогда и только тогда, когда существует обратимые матрицы размерности m × m (X) и n × n (Y) такие, что

где I_r обозначает единичную матрицу размерности r × r .

Если B – любая матрица размерности n × k, то

Если B – матрица размерности n × k ранга n, то

Если C – матрица размерности l × m ранга m, то

Неравенство Сильвестра: Если A и B матрицы размеров и , то

Это частный случай следующего неравенства.

Неравенство Фробениуса: Если AB, BC, ABC корректно определены, то

Субаддитивность:

,

когда A и B имеют одинаковые размерности.

Следствие.

• Любая матрица с рангом k может быть записана в виде суммы k матриц с рангом 1, но не меньше.

Сумма ранга и дефекта матрицы равно числу ее столбцов. (Это – теорема о ранге и дефекте.)

Линейное преобразование и ранг матрицы[править | править код]

Пусть  — матрица размера над полем (или ). Пусть  — линейное преобразование, соответствующее в стандартном базисе; это значит, что . Ранг матрицы  — это размерность образа преобразования .

Методы[править | править код]

Существует несколько методов нахождения ранга матрицы:

Метод элементарных преобразований. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Метод окаймляющих миноров. Пусть в матрице найден ненулевой минор -го порядка . Рассмотрим все миноры -го порядка, включающие в себя (окаймляющие) минор ; если все они равны нулю, то ранг матрицы равен . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

Литература[править | править код]

• Эрнест Винберг. Курс алгебры (5 сентября 2017). Дата обращения: 24 августа 2018.

Содержание:

Элементарные преобразования матриц:

Рассмотрим прямоугольную матрицу:

состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец – как m-мерный вектор. Тогда матрицу А можно записать в виде:

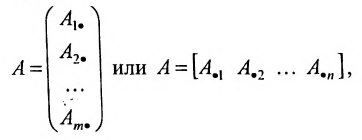
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).

Определения

Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.

Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее

Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.

При транспонировании матрицы ранг её не изменяется.

Другой метод определения ранга матрицы связан с понятием определителя.

Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: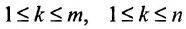 . Полагая последовательно k = 1,2,…,l, где

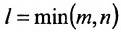, составляем при каждом k все миноры k-то порядка матрицы А. Тогда можно сформулировать еще одно определение ранга матрицы.

Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.

Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.

Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:

1. обмен местами двух строк или двух столбцов матрицы;
2. умножение всех элементов строки или столбца матрицы на произвольное число 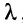, не равное нулю;
3. прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
4. исключение из матрицы строки или столбца, состоящего из нулей.

Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.

Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:

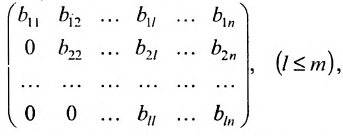
где элементы 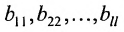отличны от нуля, а все элементы, стоящие под ними, равны нулю.

Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.

Теоремы о ранге матриц. Свойства ранга матриц

Относительно ранга матриц можно сформулировать следующие теоремы:

Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка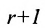(окаймляющие миноры) равны нулю, то ранг этой матрицы равен r.

Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.

Теорема: Элементарные преобразования не меняют ранга матрицы.

Доказательство теоремы следует из определения ранга матрицы и свойств определителей.

Пример:

Найти ранг матрицы: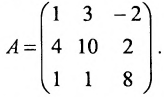

Решение:

Минор первого порядка в левом верхнем углу равен 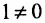. Окаймляющий его минор второго порядка:

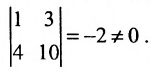Вычисляем окаймляющий его минор третьего порядка: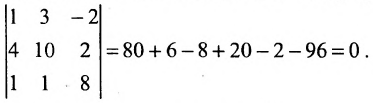

Значит ранг матрицы равен 2.

Пример:

Найти ранг матрицы:

Решение:

При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:

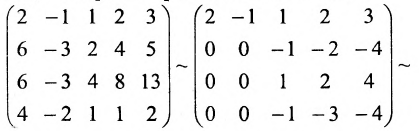
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:

(поменяем местами третью и четвертую строки)

(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 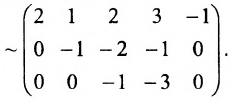Преобразовали матрицу к ступеньчатому виду, у которой на диагонали три ненулевых элемента. Ранг матрицы равен 3.

Отмстим некоторые свойства ранга матриц.

1. Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
2. Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
3. Любую матрицу С ранга r можно представить в виде произведения 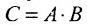, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
4. Ранг произведения матриц порядка n удовлетворяет неравенству .

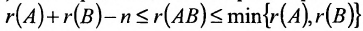Определение системы m линейных уравнений с n неизвестными

Системой m линейных уравнений с n неизвестными 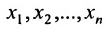называется система вида:

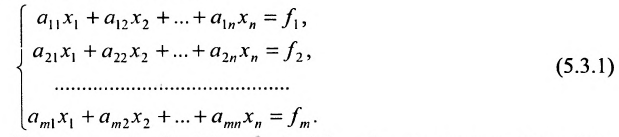
Числа 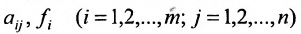называются соответственно коэффициентами системы и ее свободными членами. Первый индекс i коэффициента 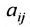соответствует номеру уравнения, в которое входит этот коэффициент, а второй индекс – номеру неизвестной 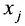, при которой стоит этот коэффициент. Индекс свободного члена 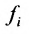соответствует номеру уравнения, содержащего .

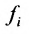С помощью знака суммирования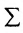 систему (5.3.1) можно записать в виде:

Матрица

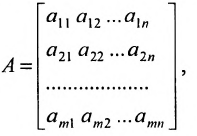
составленная из коэффициентов системы 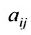, называется матрицей

системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 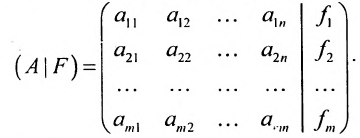Обозначив матрицу-столбец неизвестных 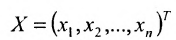и матрицу-столбец свободных членов 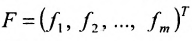, систему (5. 3.1) можно записать в матричной форме:

где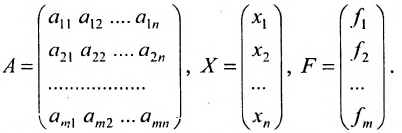

Используется также табличная форма записи системы (5.3.1):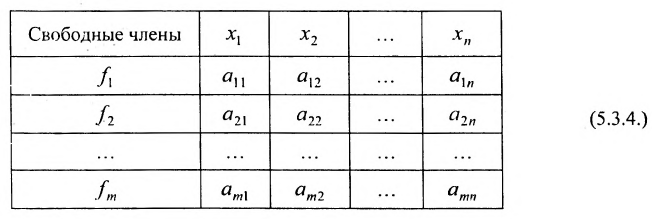

Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.

Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 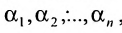, который при подстановке в (5.3.1) вместо неизвестных 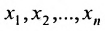, обращает каждое из уравнений системы в верное равенство.

Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы уравнений с одинаковыми наборами неизвестных 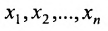называются равносильными, если они имеют одно и то же множество решений.

Отмстим, что для любой системы (5.3.1) возможны только три случая:

1. система (5.3.1) имеет единственное решение;
2. система (5.3.1) имеет бесчисленное множество решений;
3. система (5.3.1) несовместна.

Множество всех решений системы (5.3.1) называется ее общим решением.

Решить систему (5.3.1) – значит найти ее общее решение.

Пример:

Пусть задана система

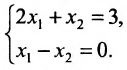
Тогда эту систему можно записать в матричном виде:

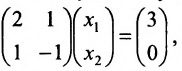
или в виде таблицы:

Система определенная, так как она имеет единственное решение 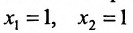. Других решений быть не может, так как прямые

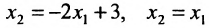на координатной плоскости 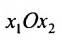пересекаются в единственной точке.

Экономические задачи, приводящие к системе линейных уравнений

Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 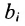представляет собой суммарную мощность цеха i, и 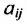— часть производственного аппарата цеха i, которая необходима для производства единицы продукции вида j. Тогда обозначив через 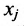количество выпущенной продукции, получим систему уравнений, показывающих. как можно использовать имеющиеся мощности в полном объёме.

Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.

При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.

Если обозначить через:

то систему уравнений баланса можно записать в виде:

или в матричной форме:

где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А – матрица коэффициентов прямых затрат.

Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:

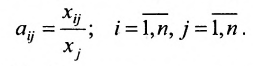
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.

Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.

Определение ранга матрицы

Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 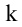строк и 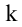столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу 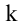-го порядка. Определитель этой матрицы называется минором 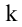-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел 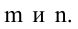Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен 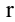, то это означает, что в матрице А имеется отличный от нуля минор порядка 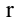, но всякий минор порядка, большего чем 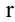, равен нулю. Ранг матрицы А обозначается через 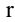(А).

Очевидно, что выполняется соотношение

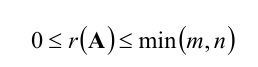
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 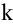-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (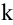+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен .

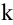Элементарными называются следующие преобразования матрицы:

1. перестановка двух любых строк (или столбцов),
2. умножение строки (или столбца) на отличное от нуля число,
3. прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы

равны нулю, например,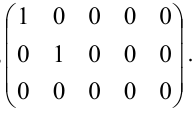

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

• Заказать решение задач по высшей математике

Пример:

Найти методом окаймления миноров ранг матрицы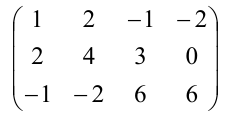

Решение:

Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 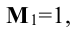расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор 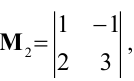отличный от нуля.

Переходим теперь к минорам 3-го порядка, окаймляющим 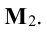Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:

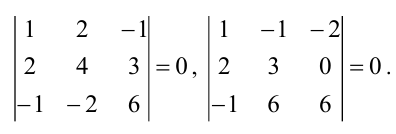
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Пример:

Найти ранг матрицы 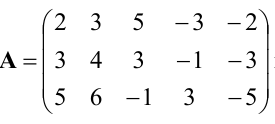и привести ее к каноническому виду.

Решение:

Из второй строки вычтем первую и переставим эти строки: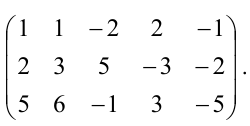

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5: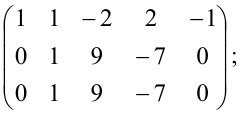

из третьей строки вычтем первую; получим матрицу 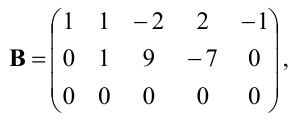которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и 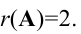Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

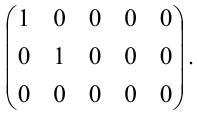
Вычисление ранга матрицы

Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А

Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.

Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,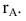

Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.

Рассмотрим некоторые методы вычисления ранга матрицы.

Метод окаймляющих миноров

Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.

Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.

В примерах выше мы говорили об уникальности столбцов и строк. Ту же самую уникальность в математике обозначают еще одним термином — линейная независимость.

Сопоставим уже знакомый термин с новым понятием:

Другими словами, при линейной зависимости значения зависят друг от друга — из значений первой строки мы можем получить значения второй.

Все эти принципы будут работать, даже если мы представим матрицу как набор точек на графике.

Возьмем такой пример:

Опишем векторы так:

Здесь мы видим, что вектор

линейно зависит от

и

.

Также обратите внимание, что:

Используя только векторы

и

, мы можем достичь любого места на плоскости. Когда векторы линейно независимы и охватывают все пространство, их называют базисом этого пространства.

В нашем случае векторы

и

— это базис плоскости, потому что двумерное пространство часто называют плоскостью. Именно поэтому

и

так же полезны, как и оси

. То же самое можно сказать о любых двух линейно независимых векторах в двумерной плоскости.

Самая простая пара линейно независимых векторов — это

и

. Вместе они образуют матрицу

:

По сути, они образуют привычные оси

:

А теперь посмотрим на самые простые линейно независимые векторы в трехмерном пространстве. Матрица будет выглядеть так:

А так выглядит сам график:

Показать четырехмерное пространство на картинке не получится, но сама матрица выглядит так: