Как можно найти скорость движения - Сайт, где вы сможете решить свои вопросы

Как можно найти скорость движения

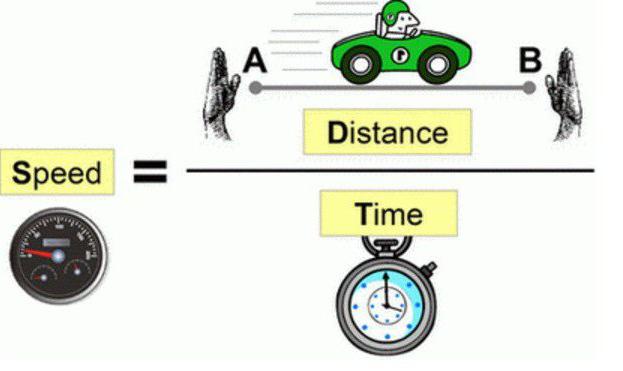
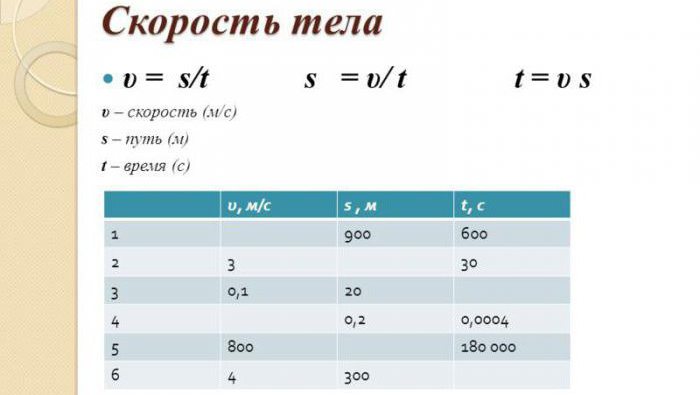
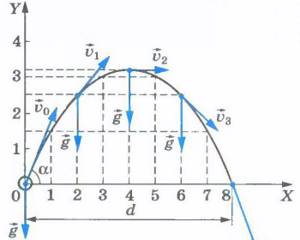
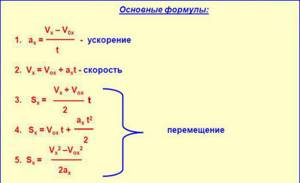
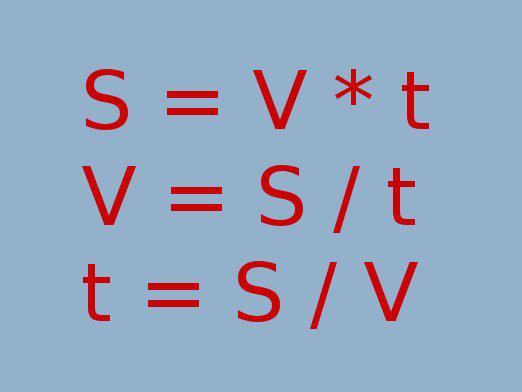Формулы скорости, времени, расстояния?

Как выразить эти понятия друг одно через другие?

Анонимный вопрос

2 ноября 2018 · 236,9 K

Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.

Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).

Выразить скорость из этой формулы можно следующим образом: v=S/t

А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v

204,1 K

Комментировать ответ…Комментировать…

V = S : t
t = S : V
S = V * t
S = расстояние
V = скорость
t = время
: = деление
* = умножение
Пример :
Решил найти расстояние ( S)
Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа
Ответ : 16 км Читать далее

21,3 K

Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?

Комментировать ответ…Комментировать…

Учусь в гимназии №17. Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021

(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.) Читать далее

20,1 K

Комментировать ответ…Комментировать…

Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

5,7 K

Комментировать ответ…Комментировать…

Короче!
Если у вас расстояние нужно найти то:
S=t*v, S=50*20(пример)
Если нужно найти время то:
t=S:V
Если нужно найти скорость то :
V=S:T.
Это все формулы. Читать далее

59,9 K

спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!

Комментировать ответ…Комментировать…

Источник

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой S.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

Показатели скорости чаще всего выражаются в м/сек; км/час.

Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.

Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Единицами времени могут быть секунды, минуты, часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

Эта формула пригодится, если нужно узнать за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.

Скорость

Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая –медленее; один человек идет быстрым шагом, другой – не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то определенное время. Допустим, что скорость человека 5 км/ч. То есть за 1 час он прошел 5 километров.

Как находить скорость, время, расстояние? Начнем со скорости. Посмотрите внимательно, в чем она измеряется? Естественно, км/ч, м/с. Существуют и другие единицы измерения, например, км/с (в космонавтике), мм/ч (в биохимии). Обратите внимание на то, что стоит перед знаком «/» и после. Во-первых, он означает «дробь», а значит, в числителе – мм, км, м, в знаменателе – ч, с, мин. Во-вторых, кажется это напоминает формулу, не правда ли? Километры, метры – расстояние, длина, а час, секунда, минута – время. Вот вам и подсказка. Чтобы проще было запомнить, как находить скорость, посмотрите не единицы измерения (км/ч, м/с). Одними словами:

Время

Что из себя представляет время? Разумеется, оно зависит от скорости. Например, вы ждете у порога дома маму и старшего брата. Они идут из магазина. Брат дошел намного раньше. Маму пришлось ждать еще минут 5. Почему? Потому что они шли с разной скоростью. Разумеется, чтобы быстрее добраться до места назначения, нужно прибавить скорость: ускорить шаг, надавить на «газ» в авто посильнее, разогнаться на велосипеде. Только при спешке будьте осторожны и бдительны, чтобы не врезаться в кого-то или во что-то.

Как находить время? У скорости есть подсказка – км/ч. А как быть со временем? Во-первых, время измеряется в минутах, секундах, часах. Формула «скорость, время, расстояние» здесь преображается следующим образом:

время t[сек., мин., ч]=S[м, мм, км]/v[м/с, мм/мин, км/ч].

Если преобразовать дробь по всем правилам математики, сократить параметр расстояния (длины), то останется только секунда, минута или час.

Расстояние, длина пройденного пути

Здесь будет легче сориентироваться, скорее всего, автомобилистам, у которых есть счетчик пробега в машине. Они смогут определить, сколько километров проехали, а еще и скорость знают. Но так как движение неравномерное, то установить тоное время перемещения не получится, если только мы возьмем среднюю скорость.

Формула пути (расстояния) – произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время. Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».

Не упустите!

Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:

Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут – это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.

Вот так легко запоминается формула «скорость, время, расстояние». Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.

Памятка по математике для учащихся 4 класса по теме » Скорость, время, расстояние»

Скачать:

pamyatka_skorost_vremya_rasstoyanie.docx 13.56 КБ

Предварительный просмотр:

по математике 4 класс по теме

«Скорость, время, расстояние»

S – расстояние ( путь); измеряется в км, м и т.д.

V – скорость ( это расстояние, преодолеваемое за единицу времени); измеряется в км/ч, м/ мин и т.д.

t- время ; измеряется в часах, минутах и т.д.

Чтобы найти расстояние, нужно скорость умножить на время. S =V х t
Чтобы найти скорость , нужно расстояние разделить на время.

Чтобы найти время , нужно расстояние разделить на скорость.

Задача на нахождение расстояния

Пешеход шёл со скоростью 5 километров в час. Какой путь он пройдёт за 3 часа?

Ответ: 15 километров пройдёт пешеход.

Задача на нахождение скорости

Пешеход за 3 часа прошёл 15 километров. С какой скоростью шёл пешеход?

Ответ: 5 км/ ч скорость пешехода.

Задача на нахождение времени

Пешеход шёл со скоростью 5 километров в час и прошёл 15 километров. Сколько времени шёл пешеход?

Ответ: 3 часа шёл пешеход.

По теме: методические разработки, презентации и конспекты

Урок разработан в соответствии с ФГОС. По типу уроков является проблемным.

Презентация к уроку 5 4 класс учебник М.З. Биболетова — содержит материал для фонетической и лексической разминки, грамматические задания и правила «Построение специальных вопросов».

Презентация выполнена к уроку окружающего мира в 4 классе, УМК «Гармония» по теме «Время: Как человек научился считать время».

Решение задач на время, повторение видов углов, и таблиц единиц длины, массы, площади.

Проверочная работа по теме «Время» для 2 класса, система развивающего обучения Занкова. В работе два варианта, в каждом шесть заданий. Задание №1 (Реши задачу) обязательно для всех. Из остальных .

Методическая разработка открытого урока «Простое прошедшее время» включает в себя план-конспект к уроку и презентацию по уроку.

Контрольная работа состоит из 6 заданий, которые включают в себя не только повторение грамматики, но и лексики. В работе используется лексика по теме: «Погода». Также есть задание на обобщение.

Определение и формула скорости

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $bar$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

Следовательно, вектор скоростив декартовых координатах можно представить:

где $bar, bar, bar$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

в сферической системе координат:

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). При равномерном движении скорость можно вычислить, применяя формулу:

где s– длина пути, t – время, за которое материальная точка преодолела путь s.

При ускоренном движении скорость можно найти как:

Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:

где $bar_0$ – начальная скорость движения, $bar = const$ .

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: [v]=м/с 2

Примеры решения задач

Задание. Движение материальной точки А задано уравнением: $x=2 t^<2>-4 t^<3>$ . Точка начала свое движение при t₀=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

Формула скорости не по зубам? Тебе ответит эксперт через 10 минут!

Задание. Скорость материальной точки является функцией от времени вида:

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$ begin 10 t-t^<2>=10(2.2) t_<1>=5+sqrt <15>approx 8,8(c) ; t_<2>=5-sqrt <15>approx 1,13(c) end $$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

При решении уравнения (2.3) нам подойдет корень равный:

Ответ. 1) $x=0 mathrm<

m>$ 2) $t_<1>=8,8 mathrm, t_<2>=1,13 c, t_<3>=11 c$

Класс: 4

Цели:

закрепить знания нахождения скорости, времени, расстояния;

ввести формулы;

учиться решать задачи с этими величинами по формулам и без них;

развивать мышление и память;

прививать любовь к математике.

1. Организация учащихся.

2. Сообщение темы.

— Сегодня на уроке мы закрепим знания нахождения скорости, времени, расстояния. Будем учиться решать задачи с помощью формул.

— А работать мы будем в форме соревнований трех команд:

1 ряд — автомобилисты

2 ряд — летчики

3 ряд — мотоциклисты

— Баллы будем выставлять на доске

3. Соотнести записи с картинкой.

— Как вы думаете, что написано на доске? (Скорости)

— Соотнесите их с нужной картинкой.

(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50 км/ч,250 км/ч.

Автобус, самолет, ракета, пешеход, поезд, велосипедист , автомобиль, пароход, мотоциклист) Каждая команда выставляет по 3 ученика.

— Как вы понимаете км/сек, км/ч, м/мин.

а) В тетрадь записываете ответ с наименованием.

Таблица на интерактивной доске.

Вложение	Размер

Скорость
V

Время
t

Расстояние
S

5 м/с

15 сек.

? м.

Муха летела со скоростью 5 м/сек. 15 сек. Какое расстояние она пролетела?

— Повторите вопрос задачи.

— Как найти расстояние?

— Кто может записать буквами это правило?

— Запишите эту формулу в тетрадь s=v * t.

Скорость
V

Время
t

Расстояние
S

? м/с

3 сек.

78 м.

За 3 сек. Сокол пролетел 78 метров. Какова скорость сокола?

— Повторите вопрос задачи.

— Как найти скорость?

— Кто может записать буквами это правило?

— Запишите эту формулу в тетрадь v=s:t.

Скорость
V

Время
t

Расстояние
S

10 м./сек

? сек.

100 м.

Грач пролетел 100 метров со скоростью 10 м/сек. Сколько времени он был в пути?

— Повторите вопрос задачи.

— Как найти время?

— Кто может записать буквами это правило?

— Запишите эту формулу в тетрадь t=s:v.

б) Составление задач.

1 ряд — нахождение V
2 ряд — нахождение t
3 ряд — нахождение S

в) Заполнить таблицу.

Скорость
V

Время
t

Расстояние
S

90 км/ч

6 ч.

? км.

? км/ч

30 ч.

1500 км

70 м/мин.

? мин.

840 м

Решение записываете в тетрадь с наименованием, рядом записываете формулу.

1500:30=50 (км/ч) v=s:t

4. Работа с учебником.

Коллективное решение задачи стр. 60 №4

Две бабы-яги поспорили, что быстроходнее ступа или помело? Одну и ту же дистанцию в 228 км баба-яга в ступе пролетела за 4 ч, а баба яга на помеле за 3 ч. Что больше, скорость ступы или помела?

а) составление таблицы.

Скорость
V

Время
t

Расстояние
S

ступа

помело

б) решение у доски и в тетрадях.

1) 288:4=72 (км/ч) — скорость ступы

2) 288:3=96 (км/ч) — скорость помела

3) 96-72=24 (км/ч) — больше скорость помела, чем скорость ступы.

Ответ запишите самостоятельно.

6. Задача повышенной сложности.

Это очень интересно (на доске написана задача)

— Кто видел счетчик в автомобиле, который ведет отчет километров, которые проехал автомобиль?

— Как он называется (спидометр).

Счетчик автомобиля показал 12921 км. Через 2 час на счетчике опять появилось число, которое читалось одинаково в обоих направлениях. С какой скоростью ехал автомобиль?

1) 13031 — 12921=110 (км) — проехал за 2 ч.

2) 110 :2 = 55 (км/ч) — скорость автомобиля.

— Как найти расстояние, скорость, время (формула).

Молодцы! Всем огромное спасибо!

Туристы ехали в первый день 5 ч. На лодке со скоростью 12 км/ч. Во второй день они были в пути столько же времени, увеличив скорость на 3 км/ч. Сколько километров проехали туристы на лодке во второй день?

Самостоятельно заполнить таблицу и решить задачу.

Ввиду того что такая физическая величина, как скорость, фигурирует во многих задачах, имеющих связь с разделами механики (а именно кинематикой и динамикой), вопрос “как найти скорость” является достаточно актуальным. И эта тенденция будет сохраняться дальше, поскольку вопрос нахождения скорости (хоть она будет начальной, хоть конечной, хоть мгновенной, которая является обобщенной вариацией этих двух скоростей) останется актуальным еще надолго. А раз так, то следует узнать о скорости как физической величине все, что пригодится в последующем для решения задач.

Где упоминается скорость тела?

На самом деле, в реальном мире мы сталкиваемся со скоростью ежесекундно. Если так подумать, на Земле постоянно что-то да находится в движении. Вы можете попробовать возразить, ограничившись, например, пределами своей комнаты. То есть, по мнению некоторых людей, ночью в комнате ничего не движется. Кровати, шкафы, стулья, стол и прочие предметы находятся на своих местах, в то время как сам человек спит, то есть не движется.

Следовательно, скорость любого элемента данной системы (комнаты, как мы условились считать) равна нулю. Да, в этом что-то есть, и с одной стороны, человек, выдвинувший такое предположение, мог оказаться правым. Но не следует забывать о том, что своеобразную систему представляет собой сама наша планета Земля, а не только предметы, которые на ней находятся. А ведь все мы знаем, что ежесекундно Земля вращается вокруг своей оси. В этой системе отсчета все тела, находящиеся в пределах планеты, также совершают движение. Поэтому говорить о том, что предмет, который, казалось бы, не двигается, находится в абсолютном покое, нельзя. Это первое, что нужно было бы сказать о скорости тела.

С детской скамьи мы учимся решать много задач не только физического, но и математического характера. Их в настоящее время не так много, и ставка делается больше на гуманитарные дисциплины наподобие иностранного языка, хотя они не должны преподаваться в ущерб родному языку и техническим дисциплинам. Но речь немного не об этом. Так вот, понятие скорости тела мы можем встретить не только в задачах по физике, хотя там она встречается, пожалуй, наиболее часто. Несколько реже, но все же фигурирует скорость тела и в задачах по математике.

Наверняка все помнят эти до ужаса ненавистные (в большинстве случаев) задачи, в которых требовалось найти, через сколько времени встретятся два автомобиля, если они движутся с такими-то скоростями. Условия при этом могут быть самые разные. То движение происходит по круговой траектории (спортсмены на велосипедах или мотоциклах), то по прямолинейной траектории. В общем, задач множество. И как бы там ни было, а наша задача заключается в том, чтобы понять, что нужно делать, столкнувшись с вопросом о том, как найти скорость в том или ином случае.

Скорость в физике

Нередко ученики, которые впервые (а возможно и повторно) знакомятся с азами (можно их так назвать) кинематики, задаются вопросом о том, как найти начальную скорость. Это действительно важно, поскольку множество задач из первой части материалов, которые предлагаются ученику для самостоятельного решения на экзамене в 9 и 11 классе, имеют целью нахождение начальной скорости либо величин, каким-либо образом связанных с ней.

Да и вообще, хотелось бы отметить, что в определенных случаях знание формул кинематики (в том числе и формулы начальной скорости при соответствующем виде движения) поможет решить даже задачу из последней части. Разумеется, на соответствующую тему. Итак, как найти начальную скорость в задачах по физике? Давайте вспомним, какие формулы даются в разделе кинематики для использования их в целях нахождения неизвестных величин.

Виды движения

Как известно, движение может быть равномерным, а может быть равноускоренным (равнозамедленным). Если из названия непонятно, каковы различия всех этих трех видов движения, то попробуем объяснить более конкретно. Равномерным движением называется движение, осуществляемое при постоянной скорости тела или материальной точки. В то же время равноускоренным движением называется движение, осуществляемое при наличии постоянного ускорения. Равнозамедленное движение – аналог равноускоренного, только ускорение при этом будет отрицательным.

На деле все выглядит так. При равномерном движении есть постоянная скорость, но ускорение отсутствует. Оно равно нулю. Тело при этом за одинаковые промежутки времени будет проходить одинаковые расстояния (если соответствующие условия не изменяются, нет никаких внешних воздействий). О каких воздействиях идет речь? На бумаге все выглядит идеально. Посмотрели на скорость, посмотрели на дистанцию, нашли время. Вот из этих трех параметров – время, скорость, расстояние – складывается своеобразный равносторонний треугольник, на котором строятся многие задачи.

Нюансы

На деле же представим, что есть два участка дороги. Один ровный, другой с небольшими бугорками. Скорость у автомобиля пускай будет та же самая, но за счет сопротивления за один и тот же промежуток времени он пройдет на втором участке дороги расстояние меньшее, чем на первом. Однако это уже задача больше из категории динамики, где рассматриваются причины, вызывающие движение тела. Кстати, логично, что при равномерном движении его конечная и начальная скорость совпадают друг с другом, а также с мгновенной скоростью.

При равноускоренном движении все будет несколько иначе. Будет присутствовать положительное ускорение, оно будет постоянным. Но вследствие присутствия ускорения скорость будет ежесекундно изменяться. В связи с этим вопрос о том, как найти скорость в определенный момент времени при наличии ускорения в системе, становится актуальным. Для этого существуют определенные формулы.

Как найти скорость?

Чтобы найти скорость тела в определенный момент времени, найти начальную скорость или конечную, необходимо для начала разобраться с типом движения. Если оно равномерное, то все достаточно просто. Для того чтобы найти скорость в этом случае, следует просто поделить пройденное телом расстояние на прошедшее время. Это и будет ответ. Немного сложнее дело обстоит в том случае, если движение равноускоренное или равнозамедленное.

Допустим, что тело в течение некоторого периода времени ускоряется. Вот одна из формул, которая может быть применена к задаче подобного рода: S = V0t +(-) at^2/2. В выражении в качестве результата (левая часть уравнения) указано пройденное телом расстояние. В правой части у нас слева направо располагается начальная скорость, время, ускорение. Почему указаны два знака? Если тело разгоняется, ускорение будет положительным, перед слагаемым будет ставиться знак “плюс”. Если ускорение отрицательное, перед слагаемым будет ставиться знак “минус”.

Как найти скорость сближения?

Допустим, что у нас есть два тела, которые движутся с известными скоростями. В общем виде пускай это будет V1 и V2. Тогда скорость их сближения будет равна модулю разности. То есть V1 – V2, взятое со знаком “плюс”. Модуль берется для того, чтобы не вдаваться в векторные нюансы, то есть не работать с направлением скоростей, поскольку скорость, как и ускорение, — величина не скалярная, а векторная. Но усложнения в школьной программе ни к чему (по крайней мере, подобные), поэтому применяется модуль.

В этой статье мы приведем распространенную формулу в физике, связанную со скоростью, временем и расстоянием. Каким образом указать, как с помощью нее можно вычислить любой из трех компонентов? Хотите на примерах убедиться, как решать такие задачи? Тогда приступим.

Чтобы рассчитать физические величины скорость, время и расстояние, необходимо понимать, что это величины связанные с процессом движения. Движение может быть равноускоренное, равнозамедленное, равномерное. Соответственно, при равноускоренном и равнозамедленном движении, скорость тела изменяется со временем. При равномерном движении скорость тела постоянна.

Чтобы найти скорость, необходимо расстояние разделить на время. Допустим, обозначим, что эти символы означают: V – c корость, s — путь, t — время. V = S / t. Например, время за которое движется поезд 2 часа. Он прошёл расстояние 120 км/ч. Какова скорость с которой шёл поезд? Решение : 120/2=60 км/ч
Чтобы найти путь, необходимо скорость умножить на время. Символы означают: V – cкорость, s — путь, t — время. S = V * t. Пример: скорость с которой движется автобус 120 км/ч, а время которое необходимо ему, чтобы добраться до пункта назначения — 4 часа. Какое расстояние необходимо пройти автобусу? Ответ: 120 к/ч* 4= 480 км. Вот расстояние которое прошел автобус.
Как узнать время? Используем те же самые символы. Итак V – cкорость, s — путь, t — время. t = S / v . Например, путь который проехал велосипедист 90 км со скоростью 30 км/ч. Каково время, за которое он проехал ? 90/30 =3 км/ч

Вот Вы и узнали, как найти скорость, время, расстояние. Зная расстояние и время, мы способны найти скорость. Соответственно, зная путь и скорость, мы способны вычислить расстояние. А зная скорость и расстояние – время. Таким образом, чтобы найти один из компонентов, нам необходим другой компонент.

Источник

Скорость
${vec v}={frac {{mathrm {d}}{vec r}}{{mathrm {d}}t}}$
Размерность	LT⁻¹
Единицы измерения
СИ	м/с
СГС	см/с
Примечания
вектор

Классическая механика
История…
Фундаментальные понятия Пространство Время Масса Скорость Сила Механическая работа Энергия Импульс
Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Уравнения Рауса Уравнения Аппеля Теория Купмана — фон Неймана
Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика
Учёные Галилей Кеплер Ньютон Эйлер Лаплас Д’Аламбер Лагранж Гамильтон Коши
См. также: Портал:Физика

Ско́рость (стандартное обозначение: , от англ. velocity, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. По определению, равна производной радиус-вектора точки по времени^[1]. В СИ измеряется в метрах в секунду.

В русском языке этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию вектора на касательную к траектории точки^[2]. В некоторых других языках для скалярной скорости имеются отдельные наименования, например англ. speed, лат. celeritas^{[значимость факта?]}.

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.

Понятие «скорость» в классической механике[править | править код]

Случай материальной точки[править | править код]

Вектор скорости (мгновенной скорости) материальной точки в каждый момент времени определяется как производная по времени радиус-вектора текущего положения этой точки, так что^[3]:

${vec v}={{mathrm {d}}{{vec r}} over {mathrm {d}}t}equiv v_{{tau }}{{vec tau }},$

где — единичный вектор касательной, проходящей через текущую точку траектории (он направлен в сторону возрастания дуговой координаты движущейся точки), а $v_{{tau }}equiv {dot {s}}$ — проекция вектора скорости на направление упомянутого единичного вектора, равная производной дуговой координаты по времени и именуемая алгебраической скоростью точки. В соответствии с приведёнными формулами, вектор скорости точки всегда направлен вдоль касательной, а алгебраическая скорость точки может отличаться от модуля этого вектора лишь знаком^[4]. При этом:

Пройденный точкой путь за промежуток времени от t_0 до , находится как

${displaystyle {tilde {s}}=int _{t_{0}}^{t}|{dot {s}}|,mathrm {d} t;}$

.

Когда алгебраическая скорость точки всё время неотрицательна, путь совпадает с приращением дуговой координаты за время от t_0 до (если же при этом начало отсчёта дуговой координаты совпадает с начальным положением движущейся точки, то будет просто совпадать с ).

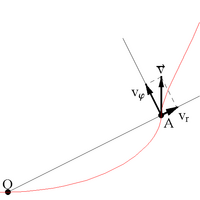
Иллюстрация средней и мгновенной скорости

Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется^[5] равномерным (алгебраическое касательное ускорение при этом тождественно равно нулю).

Предположим, что . Тогда при равномерном движении скорость точки (алгебраическая) будет равна отношению пройденного пути к промежутку времени $t-t_{0}$ , за который этот путь был пройден:

${{dot {s}}}^{{,{mathrm {cp}}}}={{tilde {s}} over t-t_{0}};.$

В общем же случае аналогичные отношения

${{vec v}}^{{,,{mathrm {cp}}}}={{{vec r}}-{{vec r}}_{0} over t-t_{0}}equiv {Delta {{vec r}} over Delta {t}}$

и ${{dot {s}}}^{{,{mathrm {cp}}}}={s-s_{0} over t-t_{0}}equiv {Delta {s} over Delta {t}}$

определяют соответственно среднюю скорость точки^[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах и говорят (чтобы избежать путаницы) как о мгновенных скоростях.

Различие между двумя введёнными выше понятиями средней скорости состоит в следующем. Во-первых, ${{vec v}}^{{,,{mathrm {cp}}}}$ — вектор, а ${{dot {s}}}^{{,{mathrm {cp}}}}$ — скаляр. Во-вторых, эти величины могут не совпадать по модулю. Так, пусть точка движется по винтовой линии и за время своего движения проходит один виток; тогда модуль средней скорости этой точки будет равен отношению шага винтовой линии (то есть расстояния между её витками) ко времени движения, а модуль средней алгебраической скорости — отношению длины витка ко времени движения.

Случай тела конечных размеров[править | править код]

Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны^[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.

Начальная скорость[править | править код]

Начальная скорость ( ${displaystyle {vec {v}}_{0}}$ ) — это скорость материальной точки в момент, принимаемый за нуль по шкале времени (то есть при t = 0 )^[8].

Истолкование ${displaystyle {vec {v}}_{0}}$ как скорости, с которой тело начинает движение, не вполне корректно, поскольку покоившееся тело в принципе не может начать двигаться с отличной от нуля скоростью. При такой формулировке неявно подразумевается, что в короткий промежуток времени действовала большая по величине сила, на пренебрежимо малом участке разогнавшая тело до скорости ${displaystyle {vec {v}}={vec {v}}_{0}}$ к моменту t = 0 .

Запись скорости в разных системах координат[править | править код]

В декартовых координатах[править | править код]

В прямоугольной декартовой системе координат^[9]:

${displaystyle mathbf {v} =v_{x}mathbf {i} +v_{y}mathbf {j} +v_{z}mathbf {k} .}$

При этом , следовательно,

${displaystyle mathbf {v} ={frac {mathrm {d} (xmathbf {i} +ymathbf {j} +zmathbf {k} )}{mathrm {d} t}}={frac {mathrm {d} x}{mathrm {d} t}}mathbf {i} +{frac {mathrm {d} y}{mathrm {d} t}}mathbf {j} +{frac {mathrm {d} z}{mathrm {d} t}}mathbf {k} .}$

Таким образом, компоненты вектора скорости — это скорости изменения соответствующих координат материальной точки^[9]:

${displaystyle v_{x}={frac {mathrm {d} x}{mathrm {d} t}};v_{y}={frac {mathrm {d} y}{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}$

В цилиндрических координатах[править | править код]

Скорость в полярных координатах

В цилиндрических координатах ^[9]:

${displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=R{frac {mathrm {d} varphi }{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}$

$v_{varphi }$ носит название поперечной скорости, $v_{R}$ — радиальной.

В сферических координатах[править | править код]

В сферических координатах ^[9]:

${displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=Rsin theta {frac {mathrm {d} varphi }{mathrm {d} t}};v_{theta }=R{frac {mathrm {d} theta }{mathrm {d} t}}.}$

Для описания плоского движения иногда используются полярные координаты, которые можно рассматривать как частный случай цилиндрических (c const) или сферических (с ).

Физическая и координатная скорости[править | править код]

В аналитической механике вышеприведённые и другие криволинейные координаты играют роль обобщённых координат; изменение положение тела описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями (они могут иметь размерность отличную от м/c). Физической же скоростью является производная радиус-вектора по времени, а её составляющие в каждом случае задаются всем стоящим перед соответствующим ортом выражением.

Некоторые связанные со скоростью понятия[править | править код]

Ряд величин в классической механике выражается через скорость.

Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на её скорость

{vec p}=m{vec v}

.

Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса.

От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения^[10]^[11]:

${displaystyle T={frac {mv^{2}}{2}}+{frac {{mathcal {I}}{vec {omega }}^{2}}{2}},}$

где — масса тела, — скорость центра масс тела, — момент инерции тела, — угловая скорость тела.

Изменение скорости во времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение)^[12]:

${vec a}={frac {{mathrm {d}}{vec v}}{{mathrm {d}}t}}={vec a}_{tau }+{vec a}_{n}={frac {{mathrm {d}}|{vec v}|}{{mathrm {d}}t}}{vec e}_{tau }+{v^{2} over r}{vec e}_{n},$

где — радиус кривизны траектории точки.

Преобразования Галилея и Лоренца для скорости[править | править код]

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта была равна , а скорость системы отсчёта относительно системы отсчёта равна vec u , то скорость тела при переходе в систему отсчёта будет равна^[9]

{displaystyle {vec {v}}'={vec {v}}-{vec {u}}.}

Для скоростей, близких к скорости света, преобразования Галилея становятся несправедливы. При переходе из системы в систему необходимо использовать преобразования Лоренца для скоростей^[9]:

$v_{x}'={frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}'={frac {v_{y}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}'={frac {v_{z}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},$

в предположении, что скорость vec u направлена вдоль оси системы . В пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Скорость в релятивистской механике[править | править код]

Четырёхмерная скорость[править | править код]

Одним из обобщений понятия скорости является четырёхмерная скорость (скорость в релятивистской механике^[9]). В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю координату , где ― скорость света, ― время события. Компоненты четырёхмерного вектора скорости связаны с проекциями трёхмерного вектора скорости следующим образом^[9]:

$v_{0}={frac {c}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{1}={frac {v_{x}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{2}={frac {v_{y}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{3}={frac {v_{z}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}.$

Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса^[9].

Существует также понятие четырёхимпульс, временна́я компонента которого равна E/c (где — энергия). Для четырёхмерного импульса выполняется равенство^[13]:

${displaystyle p_{i}=m,v_{i}}$

,

где $v_{i}$ — четырёхмерная скорость.

Понятие «быстрота»[править | править код]

В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается theta ). Быстрота выражается формулой

$theta =c,{mathrm {Arth}},{frac {v}{c}}={frac {c}{2}}ln {frac {1+{dfrac {v}{c}}}{1-{dfrac {v}{c}}}},$

где — ареатангенс, или гиперболический арктангенс. Быстрота стремится к бесконечности когда скорость стремится к скорости света. В отличие от скорости, для которой необходимо пользоваться преобразованиями Лоренца, быстрота аддитивна, то есть

$theta '=theta +theta _{0},$

где $theta _{0}$ — быстрота системы отсчёта относительно системы отсчёта .

Некоторые скорости[править | править код]

Космические скорости[править | править код]

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос

Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.

В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.

Скорости распространения волн[править | править код]

Скорость звука[править | править код]

Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.

Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.

Скорость света[править | править код]

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с^[14].

Скорость гравитации[править | править код]

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.

Единицы измерения скорости[править | править код]

Линейная скорость:

Метр в секунду, (м/с), производная единица системы СИ
Километр в час, (км/ч)
узел (морская миля в час)
Число Маха, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
Скорость света в вакууме (обозначается c)

Угловая скорость:

Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
Обороты в секунду (в технике)
градусы в секунду, грады в секунду

Соотношения между единицами скорости[править | править код]

1 м/с = 3,6 км/ч
1 узел = 1,852 км/ч = 0,514 м/c
Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
c = 299 792 458 м/c

Исторический очерк[править | править код]

Две стадии движения брошенного тела по теории Авиценны: отрезок АВ — период «насильственного стремления», отрезок ВС — период «естественного стремления» (падение вертикально вниз)

Автолик из Питаны в IV веке до н. э. определил равномерное движение так: «О точке говорится, что она равномерно перемещается, если в равные времена она проходит равные и одинаковые величины». Несмотря на то, что в определении участвовали путь и время, их отношение считалось бессмысленным^[15], так как сравнивать можно было только однородные величины и скорость движения являлась чисто качественным, но не количественным понятием^[16]. Живший в то же время Аристотель делил движение на «естественное», когда тело стремится занять своё естественное положение, и «насильственное», происходящее под действием силы. В случае «насильственного» движения произведение величины «двигателя» и времени движения равно произведению величины «движимого» и пройденного пути, что соответствует формуле Ft=ms , или F=mv ^[15]. Этих же взглядов придерживался Авиценна в XI веке, хотя и предлагал другие причины движения^[17], а также Герард Брюссельский в конце XII —
начале XIII века. Герард написал трактат «О движении» — первый европейский трактат по кинематике — в котором сформулировал идею определения средней скорости движения тела (при вращении прямая, параллельная оси вращения, движется «одинаково с любой своей точкой», а радиус — «одинаково со своей серединой»)^[18].

В 1328 году увидел свет «Трактат о пропорциях или о пропорциях скоростей при движении» Томаса Брадвардина, в котором он нашёл несоответствие в физике Аристотеля и связи скорости с действующими силами. Брадвардин заметил, что по словесной формуле Аристотеля если движущая сила равна сопротивлению, то скорость равна 1, в то время как она должна быть равна 0. Он также представил свою формулу изменения скорости, которая хоть и была не обоснована с физической точки зрения, но представляла собой первую функциональную зависимость скорости от причин движения. Брадвардин называл скорость «количеством движения»^[19]. Уильям Хейтсбери, в трактате «О местном движении» ввёл понятие мгновенной скорости. В 1330—1340 годах он и другие ученики Брадвардина доказали так называемое «мертонское правило», которое означает равенство пути при равноускоренном движении и равномерном движении со средней скоростью^[20].

Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря среднему градусу, если бы тело двигалось всё время с этим средним градусом.

— «Мертонское правило» в формулировке Суайнсхеда^[20]

В XIV веке Жан Буридан ввёл понятие импетуса^[21], благодаря чему была определена величина изменения скорости — ускорение. Николай Орем, ученик Буридана, предложил считать, что благодаря импетусу ускорение остаётся постоянным (а не скорость, как полагал сам Буридан), предвосхитив, таким образом, второй закон Ньютона^[22]. Орем также использовал графическое представление движения. В «Трактате о конфигурации качеств и движения» (1350) он предложил изображать отрезками перпендикулярных прямых количество и качество движения (время и скорость), иными словами, он нарисовал график изменения скорости в зависимости от времени^[23].

По мнению Тартальи, только вертикальное падение тела является «естественным» движением, а все остальные — «насильственные», при этом у первого типа скорость постоянно возрастает, а у второго — убывает. Два этих типа движения не могут проистекать одновременно. Тарталья считал, что «насильственные» движения вызваны ударом, результатом которого является «эффект», определяемый скоростью^[24]. С критикой работ Аристотеля и Тартальи выступал Бенедетти, который вслед за Оремом пользовался понятиями импетуса и ускорения^[25].

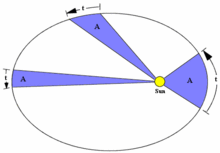
В 1609 году в работе «Новая астрономия» Кеплер сформулировал закон площадей, согласно которому секторная скорость планеты (площадь, описываемая отрезком планета — Солнце, за единицу времени) постоянна^[26]. В «Началах философии» Декарт сформулировал закон сохранения количества движения, которое в его понимании есть произведение количества материи на скорость^[27], при этом Декарт не принимал во внимание тот факт, что количество движения имеет не только величину, но и направление^[28]. В дальнейшем понятие «количество движения» развивал Гук, который понимал его как «степень скорости, присущей в определённом количестве вещества»^[29]. Гюйгенс, Валлис и Рен добавили к этому определению направление. В таком виде во второй половине XVII века количество движения стало важным понятием в динамике, в частности в работах Ньютона и Лейбница^[30]. При этом Ньютон не определял в своих работах понятие скорости^[31]. По-видимому, первая попытка явного определения скорости была сделана Валлисом в его трактате «Механика или геометрический трактат о движении» (1669—1671): «Скорость есть свойство движения, отражающееся в сравнении длины и времени; а именно, она определяет, какая длина в какое время проходится»^[32].

В XVII веке были заложены основы математического анализа, а именно интегрального и дифференциального исчисления. В отличие от геометрических построений Лейбница, теория «флюксий» Ньютона строится на потребностях механики и имеет в своём основании понятие скорости. В своей теории Ньютон рассматривает переменную величину «флюенту» и её скорость изменения — «флюксию»^[33].

Скорости в природе и технике[править | править код]

Основной источник: ^[34]

	Метры в секунду
Скорость улитки	${displaystyle 1{,}4times 10^{-2}}$
Скорость черепахи	${displaystyle 5{,}0times 10^{-2}}$
Средняя скорость здорового человека (произвольный темп)
Рекорд скорости человека в ходьбе на 50 км	()
Рекорд скорости человека в беге на дистанции 100 м	${displaystyle 1{,}0times 10^{1}}$ ( ${displaystyle 1{,}044times 10^{1}}$ )
Скорость гепарда
Максимальная скорость полёта сокола
Максимальная скорость локомотива на железной дороге
Максимальная скорость автомобиля	^[35]
Средняя скорость молекулы азота при температуре 0 °C
Максимальная скорость пассажирского реактивного самолёта
Скорость движения Луны по орбите вокруг Земли
Скорость искусственного спутника Земли
Скорость движения Земли по орбите вокруг Солнца
Скорость движения Солнца по орбите вокруг центра Галактики
Скорость электронов в кинескопе телевизора	${displaystyle 1{,}0times 10^{8}}$
Скорость движения самых далёких галактик	${displaystyle 1{,}4times 10^{8}}$
Максимальная скорость протонов в Большом адронном коллайдере	299 792 455
Скорость частицы Oh-My-God	299792457,9999999999999985310169558
Скорость безмассовых частиц (фотонов, глюонов, гравитонов)	299 792 458
Скорость тахионов и сверхбрадионов	> 299792458

Скорости движения живых существ[править | править код]

Сапсан (самое быстрое животное): самая высокая зарегистрированная скорость — 389 км/ч^[36];
Гепард (самое быстрое наземное животное): самая высокая зарегистрированная скорость — 98 км/ч^[37];
Меч-рыба: от 100 до 130 км в час^[37];
Чёрный марлин: самая высокая зарегистрированная скорость — 105 км/ч^[36];
Вилорогая антилопа: самая высокая зарегистрированная скорость — 88,5 км/ч^[36];
Лошадь (американский квортерхорс): 88 км/ч^[36];
Человек: самая высокая зарегистрированная скорость — 44,72 км/ч (Усэйн Болт)^[37].

Рекорды скорости транспортных средств[править | править код]

Самый быстрый рукотворный объект — Parker Solar Probe, 150 км/с (относительно Солнца) в 2021 году^[38].

Абсолютный рекорд скорости в воздухе был поставлен в 1976 году американским самолетом-разведчиком Lockheed SR-71 Blackbird — 3529,56 км/ч.

Рекорд скорости на земле был установлен в 2003 году на ракетных санях и составил 10 325 км/ч или 2868 м/с (по другим данным, 10 430 км/ч)^[39]

Самая высокая скорость на наземном управляемом транспортном средстве была достигнута на реактивном автомобиле Thrust SSC в 1997 году — 1228 км/ч.

Рекорд скорости на воде был поставлен в 1978 году австралийским судном с реактивным газотурбинным двигателем Spirit of Australia^[en] — 511,11 км/ч^[40]

См. также[править | править код]

Кинематика

Примечания[править | править код]

↑ Маркеев, 1990, с. 15.
↑ Старжинский, 1980, с. 154.
↑ Маркеев, 1990, с. 15—17.
↑ Старжинский, 1980, с. 154—155.
↑ Старжинский, 1980, с. 163.
↑ Старжинский, 1980, с. 152.
↑ Маркеев, 1990, с. 46—47.
↑ См. Всегда ли начальная скорость равна нулю? в справочнике «Студворк».
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ Скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь.. — 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
↑ ¹ ² Яковлев, 2001, с. 21.
↑ Яковлев, 2001, с. 34.
↑ Яковлев, 2001, с. 29.
↑ Яковлев, 2001, с. 31—32.
↑ Яковлев, 2001, с. 32—34.
↑ ¹ ² Яковлев, 2001, с. 35.
↑ Яковлев, 2001, с. 35—36.
↑ Яковлев, 2001, с. 37.
↑ Яковлев, 2001, с. 37—38.
↑ Яковлев, 2001, с. 43.
↑ Яковлев, 2001, с. 45.
↑ Яковлев, 2001, с. 51—52.
↑ Яковлев, 2001, с. 59.
↑ Яковлев, 2001, с. 68.
↑ Яковлев, 2001, с. 77.
↑ Яковлев, 2001, с. 91.
↑ Яковлев, 2001, с. 96.
↑ Яковлев, 2001, с. 72—73.
↑ Яковлев, 2001, с. 64—66.
↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44
↑ FIA World Land Speed Records (англ.). Federation Internationale de l’Automobile (10 июня 2012). Дата обращения: 3 декабря 2020. Архивировано 31 марта 2019 года.
↑ ¹ ² ³ ⁴ 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 29 июля 2021 года.
↑ ¹ ² ³ 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 22 сентября 2020 года.
↑ Самый быстрый объект, созданный человеком. Зонд Parker Solar Probe развил скорость около 150 км/с. Дата обращения: 17 июня 2022. Архивировано 17 мая 2021 года.
↑ Test sets world land speed record. www.af.mil. Дата обращения: 19 апреля 2016.
↑ Назло рекордам: почему люди не хотят передвигаться очень быстро

Литература[править | править код]

Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
Старжинский В. М. Теоретическая механика. — М.: Наука, 1980. — 464 с.
Яковлев В. И. Предыстория аналитической механики. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 328 с. — ISBN 5-93972-063-3.

Источник

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

через формулу нахождения мощности;
через дифференциальные исчисления;
по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой – нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

v – скорость объекта,
S – расстояние, которое пройдено или должно быть пройдено объектом,
t – время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S, n – количество этих участков, vср – средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

vср=(S1+S2+…+Sn)/t, где vср – средняя скорость объекта на всем протяжении пути,
S1, S2, Sn – отдельные неравномерные участки всего пути,
t – общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

vср=S/(t1+t2+…+tn), где S – общее пройденное расстояние,
t1, t2, tn – время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N – механическая мощность,

F – сила,

v – скорость,

cos α – косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v – понятно что такое,

S – расстояние, которое требуется найти,

t – время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v – все та же скорость,

S – расстояние, пройденный путь,

t – время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Источник

Загрузить PDF

Загрузить PDF

Скорость — это векторная величина, которая характеризует быстроту перемещения и направление движения предмета (тела). В математике скорость определяется как изменение положения тела в зависимости от изменения времени.^[1] Скорость можно найти во множестве физических и математических задач. Выбор правильной формулы зависит от данных значений, поэтому внимательно читайте условие задачи.

Формулы

1
2

Запишите формулу, содержащую положение и время. Скорость можно вычислить по изменению положения тела и времени. Такую формулу можно применить к любой задаче. Обратите внимание, что если скорость тела меняется, вы найдете среднюю скорость за все время движения, а не конкретную скорость в определенный момент времени.
3
Вычислите расстояние между начальным и конечным положениями. То есть между точками начала и окончания движения; они, наряду с направлением движения, указывают на «перемещение» или «изменение положения».^[3] При этом траектория движения тела между этими точками значения не имеет.
- Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
  - Автомобиль переместился на 41-5 = 36 м на восток.
- Пример 2: трамплин подбрасывает пловца на 1 метр вверх, и пловец летит до воды 5 м. Каково перемещение пловца?
  - Пловец оказался на 4 м ниже начальной точки, поэтому его перемещение равно -4 м (0 + 1 – 5 = -4). Несмотря на то, что пройденное пловцом расстояние составило 6 м (1 м вверх и 5 м вниз), конечная точка находится на 4 м ниже начальной точки.
4
Вычислите изменение времени. Время, которое потребовалось для достижения конечной точки, будет, скорее всего, дано в задаче; если нет, просто вычтите начальное время из конечного.
- Пример 1 (продолжение): в задаче сказано, что машине потребовалось 8 с, чтобы переместиться из начальной точки в конечную, поэтому изменение времени равно 8 с.
- Пример 2 (продолжение): если пловец прыгнул в момент времени t = 7 с и коснулся воды в момент времени t = 8 с, изменение времени: 8 – 7 = 1 с.
5

Разделите перемещение на изменение времени. Сделайте это, чтобы найти скорость движущегося тела. Теперь укажите направление движения, и вы получите среднюю скорость.
6
Решите задачу, когда направление движения меняется. Не во всех задачах тело движется вдоль одной линии. Если тело совершило поворот, нарисуйте схему движения и решите геометрическую задачу, чтобы найти расстояние.
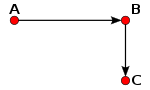
- Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
  - Нарисуйте схему и соедините начальную и конечную точки прямой линией. Это гипотенуза треугольника, которую можно найти с помощью теоремы Пифагора или других формул. В нашем примере перемещение составит 5 м на северо-восток.
  - Возможно, учитель математики попросит вас найти точное направление движения (в виде угла над горизонтальной прямой). В этом случае воспользуйтесь геометрическими законами или векторами.^[4]
Реклама

1

Запомните формулу для вычисления скорости ускоряющегося тела. Ускорение — это быстрота изменения скорости. Если ускорение постоянное, скорость меняется с одинаковой быстротой.^[5] Формула включает произведение ускорения и времени, а также начальную скорость:
2
Умножьте ускорение на изменение времени. Так вы вычислите, насколько скорость увеличилась (или уменьшилась) за это время.
- Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с². Насколько увеличится скорость лодки в течение 5 с?
  - a = 10 м/с ²
  - t = 5 с
  - (a * t) = 10 * 5 = 50 м/с.
3

Прибавьте начальную скорость. Вы нашли общее изменение скорости. Прибавьте это значение к начальной скорости тела, чтобы вычислить конечную скорость.
4
Укажите направление движения. Помните, что скорость является векторной величиной, то есть имеет направление. Поэтому в ответе укажите направление.
- В нашем примере лодка начала движение на север и не изменила направление, поэтому ее конечная скорость равна 52 м/с на север.
5
Используйте данную формулу, чтобы вычислить другие величины, которые входят в нее. Если известны ускорение и скорость в определенный момент времени, с помощью формулы можно найти скорость в другой момент времени. Например, вычислим начальную скорость:
- Поезд ускоряется на 7 м/с² в течение 4 секунд и достигает скорости 35 м/с. Какова начальная скорость поезда?
Реклама

1
Запомните формулу для вычисления круговой скорости. Круговая скорость — это скорость, которую должно иметь тело, чтобы постоянно вращаться вокруг другого тела, обладающего гравитацией, например, планеты.^[6]
- Круговая скорость равна отношению длины круглого пути к периоду времени, в течение которого тело движется.
- Формула для вычисления круговой скорости:
  - v = ^(2πr) / _T
- Обратите внимание, что 2πr — это длина окружности.
- r — радиус.
- T — период времени.
2
Умножьте радиус окружности на 2π. Сначала необходимо вычислить длину окружности. Для этого умножьте радиус на 2π. В качестве значения π можно использовать 3, 14.
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
  - r = 8 м
  - T = 45 с
  - Длина окружности = 2πr ≈ (2)(3,14)(8) = 50,24 м
3
Разделите полученное значение на время. Сделайте это, чтобы вычислить круговую скорость тела.
- Пример: v = ^(2πr) / _T = ^50,24 / ₄₅ = 1,12 м/с
  - Круговая скорость тела равна 1,12 м/с.
Реклама

Советы

Метры в секунду (м/с) — это единица измерения скорости.^[7]. Перед решением задачи убедитесь, что все единицы измерения соответствуют друг другу, например, значения даны в метрах (м), секундах (с), метрах в секунду (м/с) и метрах в квадратных секундах (м/с²).
Средняя скорость характеризует среднюю скорость, которую имеет тело на протяжении всего пути. Мгновенная скорость — это скорость тела в определенный момент времени.

Реклама

Об этой статье

Эту страницу просматривали 17 731 раз.

Была ли эта статья полезной?

Источник

Добавить комментарий Отменить ответ