Загрузить PDF
Загрузить PDF
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-

1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-

2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n – 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-

3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-

4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 – 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-

1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-

2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-

3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-

4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-

5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 237 189 раз.
Была ли эта статья полезной?
Download Article
Download Article
In geometry, an angle is the space between 2 rays (or line segments) with the same endpoint (or vertex). The most common way to measure angles is in degrees, with a full circle measuring 360 degrees. You can calculate the measure of an angle in a polygon if you know the shape of the polygon and the measure of its other angles or, in the case of a right triangle, if you know the measures of two of its sides. Additionally, you can measure angles using a protractor or calculate an angle without a protractor using a graphing calculator. This is to allow you to calculate angles
-

1
Count the number of sides in the polygon. In order to calculate the interior angles of a polygon, you need to first determine how many sides the polygon has. Note that a polygon has the same number of sides as it has angles.[1]
- For instance, a triangle has 3 sides and 3 interior angles while a square has 4 sides and 4 interior angles.
-

2
Find the total measure of all of the interior angles in the polygon. The formula for finding the total measure of all interior angles in a polygon is: (n – 2) x 180. In this case, n is the number of sides the polygon has. Some common polygon total angle measures are as follows:[2]
- The angles in a triangle (a 3-sided polygon) total 180 degrees.
- The angles in a quadrilateral (a 4-sided polygon) total 360 degrees.
- The angles in a pentagon (a 5-sided polygon) total 540 degrees.
- The angles in a hexagon (a 6-sided polygon) total 720 degrees.
- The angles in an octagon (an 8-sided polygon) total 1080 degrees.
Advertisement
-

3
Divide the total measure of all of a regular polygon’s angles by the number of its angles. A regular polygon is a polygon whose sides are all the same length and whose angles all have the same measure. For instance, the measure of each angle in an equilateral triangle is 180 ÷ 3, or 60 degrees, and the measure of each angle in a square is 360 ÷ 4, or 90 degrees.[3]
- Equilateral triangles and squares are examples of regular polygons, while the Pentagon in Washington, D.C. is an example of a regular pentagon and a stop sign is an example of a regular octagon.
-

4
Subtract the sum of the known angles from the total measure of the angles for an irregular polygon. If your polygon doesn’t have sides of the same length and angles of the same measure, all you need to do is add up all of the known angles in the polygon. Then, subtract that number from the total measure of all of the angles to find the missing angle.[4]
- For example, if you know that 4 of the angles in a pentagon measure 80, 100, 120, and 140 degrees, add the numbers together to get a sum of 440. Then, subtract this sum from the total angle measure for a pentagon, which is 540 degrees: 540 – 440 = 100 degrees. So, the missing angle is 100 degrees.
Tip: Some polygons offer “cheats” to help you figure out the measure of the unknown angle. An isosceles triangle is a triangle with 2 sides of equal length and 2 angles of equal measure. A parallelogram is a quadrilateral with opposite sides of equal lengths and angles diagonally opposite each other of equal measure.
Advertisement
-

1
Remember that every right triangle has one angle equal to 90 degrees. By definition, a right triangle will always have one angle that’s 90 degrees, even if it’s not labeled as such. So, you will always know at least one angle and can use trigonometry to find out the other 2 angles.[5]
-

2
Measure the length of 2 of the triangle’s sides. The longest side of a triangle is called the “hypotenuse.” The “adjacent” side is adjacent (or next to) to the angle you’re trying to determine.[6]
The “opposite” side is opposite to the angle you’re trying to determine. Measure 2 of the sides so you can determine the measure of the remaining angles in the triangle.[7]
Tip: You can use a graphing calculator to solve your equations or find a table online that lists the values for various sine, cosine, and tangent functions.
-

3
Use the sine function if you know the length of the opposite side and the hypotenuse. Plug your values into the equation: sine (x) = opposite ÷ hypotenuse. Say that the length of the opposite side is 5 and the length of the hypotenuse is 10. Divide 5 by 10, which is equal to 0.5. Now you know that sine (x) = 0.5 which is the same as x = sine-1 (0.5).[8]
- If you have a graphing calculator, simply type 0.5 and press sine-1. If you don’t have a graphing calculator, use an online chart to find the value. Both will show that x = 30 degrees.
-

4
Use the cosine function if you know the length of the adjacent side and the hypotenuse. For this type of problem, use the equation: cosine (x) = adjacent ÷ hypotenuse. If the length of the adjacent side is 1.666 and the length of the hypotenuse is 2.0, divide 1.666 by 2, which is equal to 0.833. So, cosine (x) = 0.833 or x = cosine-1 (0.833).[9]
- Plug 0.833 into your graphing calculator and press cosine-1. Alternatively, look up the value in a cosine chart. The answer is 33.6 degrees.
-

5
Use the tangent function if you know the length of the opposite side and the adjacent side. The equation for tangent functions is tangent (x) = opposite ÷ adjacent. Say you know the length of the opposite side is 75 and the length of the adjacent side is 100. Divide 75 by 100, which is 0.75. This means that tangent (x) = 0.75, which is the same as x = tangent-1 (0.75).[10]
- Find the value in a tangent chart or press 0.75 on your graphing calculator, then tangent-1. This is equal to 36.9 degrees.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you find an angle?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics
Expert Answer
-
Question
How do I create a 90 degree corner by swinging an arch?

Pick a convenient point on a line to be the vertex of your 90° angle. Choose two points on the line, one on each side of the vertex and equidistant from the vertex. Use a compass to draw two arcs of the same diameter, each centered on one of those latter points. Draw a line connecting the vertex point with the intersecting point(s) of the arcs. That line describes a 90° angle with the first line.
-
Question
How do I find the interior angles of a hexagon without base or height or anything?

The sum of the six interior angles of a regular polygon is (n-2)(180°), where n is the number of sides. Therefore, in a hexagon the sum of the angles is (4)(180°) = 720°. All the angles are equal, so divide 720° by 6 to get 120°, the size of each interior angle.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Angles are given names according to how many degrees they measure. As noted above, a right angle measures 90 degrees. An angle measuring more than 0 but less than 90 degrees is an acute angle. An angle measuring more than 90 but less than 180 degrees is an obtuse angle. An angle measuring 180 degrees is a straight angle, while an angle measuring more than 180 degrees is a reflex angle.
-
Two angles whose measures add up to 90 degrees are called complementary angles. (The two angles other than the right angle in a right triangle are complementary angles.) Two angles whose measures add up to 180 degrees are called supplementary angles.
Advertisement
References
About This Article
Article SummaryX
To calculate the angles inside a polygon, first count the number of interior angles. A polygon has the same number of interior angles as sides. For example, a triangle always has 3 angles, while a square or rectangle always has 4, and so on. Next, use the formula (n – 2) x 180 to find the total number of degrees of all the interior angles combined. In this formula, n is equal to the number of interior angles. So, a triangle would have (3 – 2) x 180 degrees, or 180 degrees total. On the other hand, a quadrilateral, such as a square or a rectangle, would have (4 – 2) x 180 degrees, or a total of 360 degrees. If the polygon is regular—that is, if all the sides are the same length—then all you have to do is divide the total number of degrees of all the interior angles by the number of sides in the polygon. For instance, to calculate the angles in a regular pentagon, divide 540 degrees by 5 to get 108. Each angle in the pentagon is 108 degrees. If the polygon has irregular sides, your job is a little trickier. If you know all the angles in the polygon but one, you can add the known angles up and subtract the sum from the total number of degrees of all the interior angles. This will give you the number of degrees in the missing angle. In other cases, you may need to look up a formula or function that’s specific to the type of polygon you’re working with. For instance, you can use a sine, cosine, or tan function to find the angles in a right triangle depending on which angle you’re calculating and which side lengths you know. To find out how to calculate angle measure in a right triangle, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 691,722 times.
Reader Success Stories
-

Cynthia Trent
Dec 29, 2022
“I was doing my homework and I didn’t understand something, so now it helped me.”
Did this article help you?
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
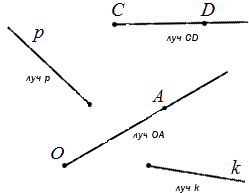
Перейдем к понятию определения угла.
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
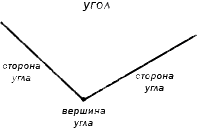
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.
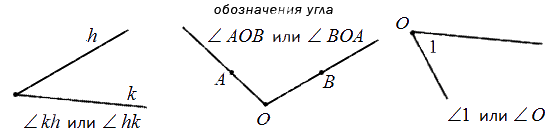
Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
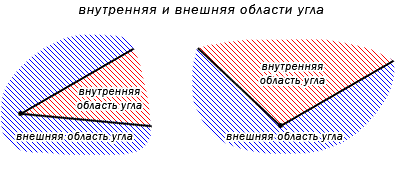
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
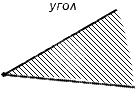
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
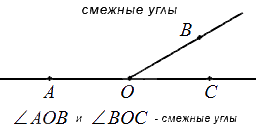
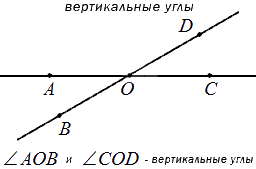
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
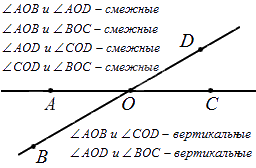
Сравнение углов
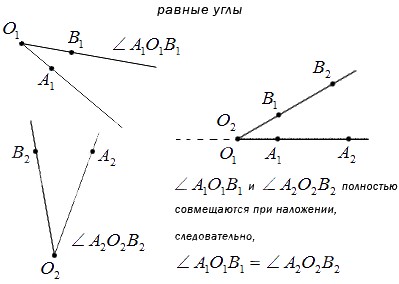
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
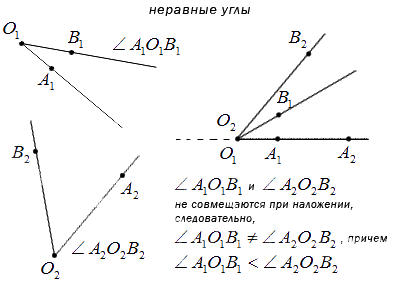
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи «°», тогда один градус – 1° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
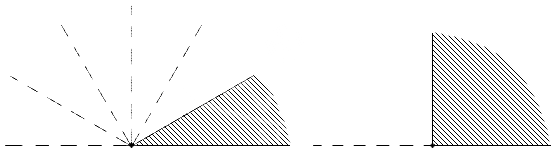
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают «’», а секунды «”». Имеет место обозначение:
1°=60’=3600”, 1’=(160)°, 1’=60”, 1”=(160)’=(13600)° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17°3’59” .
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17°3’59” . Запись имеет еще один вид 17+360+593600=172393600.
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠AOB и его градусной мере в 110 градусов применяют более удобную запись ∠AOB=110° , которая читается «Угол АОВ равен 110градусам».
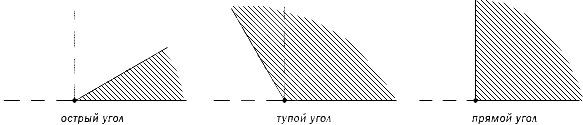
В геометрии используется мера угла из интервала (0,180], а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0,90), а тупой – (90,180). Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так:∠AOB=∠AOC+∠DOB=45°+30°+60°=135° .
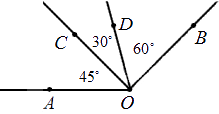
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
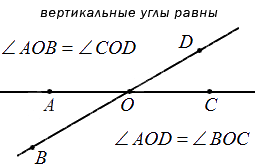
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол АОВ и СОD – вертикальные (на чертеже), тогда пары углов АОВ и ВОС, СОD и ВОС считают смежными. В таком случает равенство∠AOB+∠BOC=180° вместе с ∠COD+∠BOC=180° считаются однозначно верными. Отсюда имеем, что ∠AOB=∠COD . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы ОА и ОВ. По определению данный треугольник AOB является равносторонним, значит длина дуги AB равна длинам радиусов ОВ и ОА.
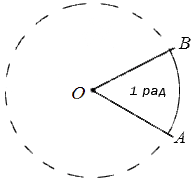
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
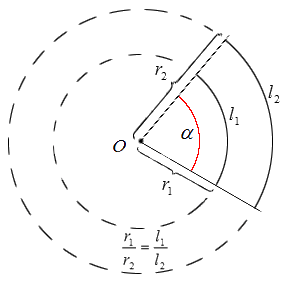
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
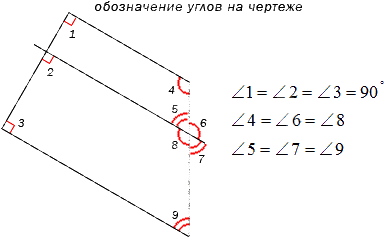
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
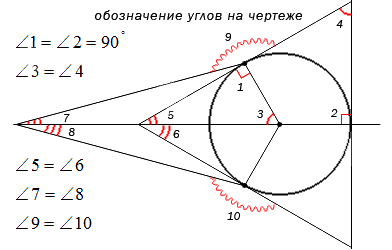
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
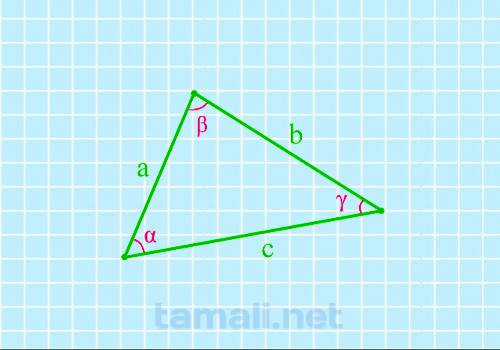
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
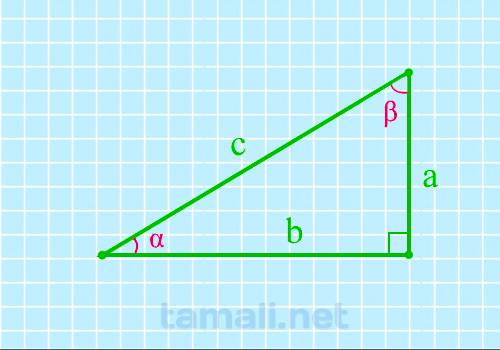
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
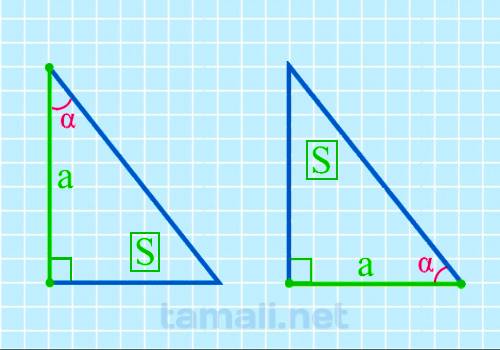
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
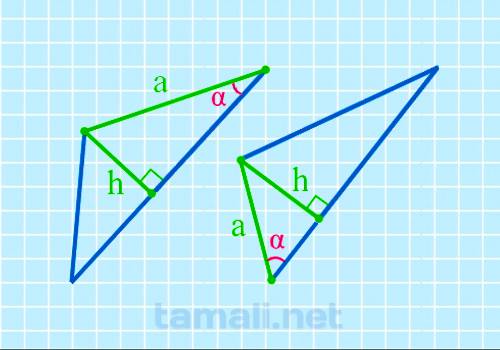
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
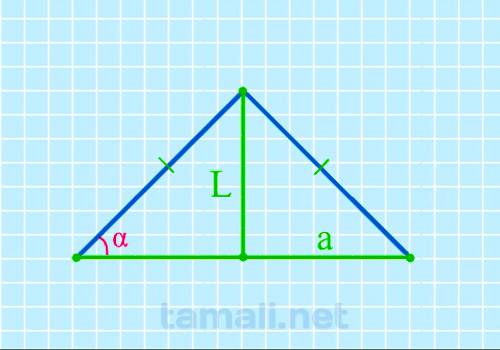
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
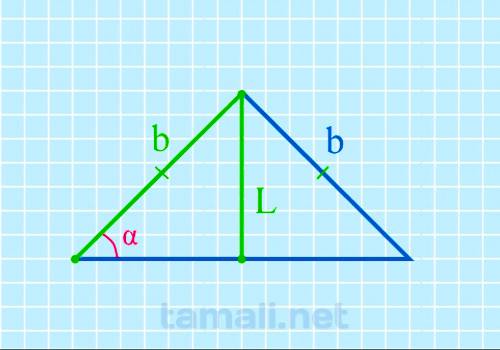
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
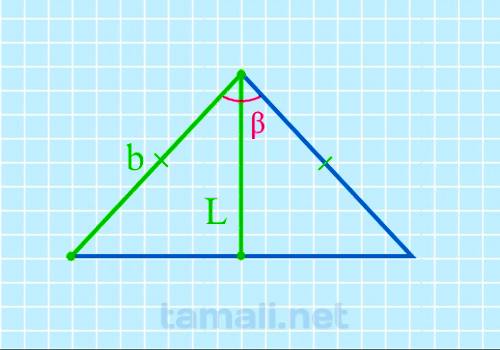
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
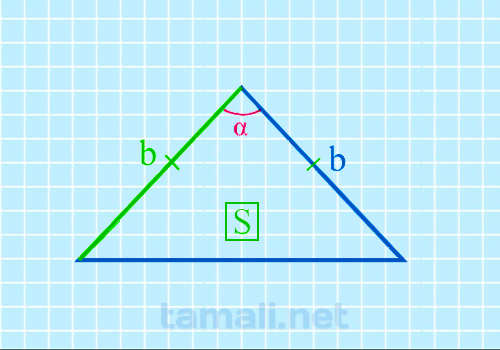
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
У этого термина существуют и другие значения, см. Угол (значения).
| Угол | |
|---|---|
| ∠ | |
| Размерность | безразмерная |
| Единицы измерения | |
| СИ | радиан |
| Другие единицы | градус, минута, секунда, град, тысячная |
У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла)[1].
Общие сведения[править | править код]

Два луча (BA и ВС), выходящие из общей вершины B, образуют на плоскости две области, являющиеся внутренними областями двух плоских углов
Плоскость, содержащая обе стороны угла, делится углом на две области. Каждая из этих областей, объединённая со сторонами угла, называется плоским углом (или просто углом, если это не вызывает разночтений). Один из плоских углов (обычно меньший из двух) иногда условно называют внутренним, а другой — внешним. Точки плоского угла, не принадлежащие его сторонам, образуют внутреннюю область плоского угла.
В другом, эквивалентном варианте определения плоским углом называется часть плоскости, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую лежащую в этой плоскости линию (которая называется линией, стягивающей данный плоский угол).
Часто для краткости углом называют также угловую меру, то есть число, определяющее величину угла.
Кроме наиболее часто встречающихся плоских углов, в качестве углов могут рассматриваться и более общие объекты — фигуры, образованные пересекающимися дугами, полуплоскостями и другими фигурами как в евклидовой, так и в других типах геометрии в метрических пространствах различной размерности.
Обозначение углов[править | править код]

«∠», обозначение угла в геометрии

Для обозначения угла имеется общепринятый символ: 
В математических выражениях углы часто обозначают строчными греческими буквами: α, β, γ, θ, φ и др. Как правило, данные обозначения также наносятся на чертёж для устранения неоднозначности в выборе внутренней области угла. Чтобы избежать путаницы с числом пи, символ π, как правило, для этой цели не используется. Для обозначения телесных углов (см. ниже) часто применяют буквы ω и Ω.
Также часто угол обозначают тремя символами точек, например 



См. вариации и обобщения.
Реже используются обозначения прямых, образующих стороны угла. Например, 


Так, для рисунка справа записи γ, 

Иногда для обозначения углов используются строчные латинские буквы (a, b, c, …) и цифры.
На чертежах углы отмечаются небольшими одинарными, двойными или тройными дужками, проходящими по внутренней области угла с центрами в вершине угла. Равенство углов может отмечаться одинаковой кратностью дужек или одинаковым количеством поперечных штрихов на дужке. Если необходимо указать направление отсчёта угла, оно отмечается стрелкой на дужке. Прямые углы отмечаются не дужками, а двумя соединёнными равными отрезками, расположенными таким образом, что вместе со сторонами они образуют небольшой квадрат, одна из вершин которого совпадает с вершиной угла.
Угловая мера[править | править код]
Угловая мера, позволяющая сравнивать плоские углы, может быть введена следующим образом. Два плоских угла называются равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их вершины и обе стороны. От любого луча на плоскости в данную сторону можно отложить единственный угол, равный данному. Если один угол может быть размещён полностью внутри другого угла таким образом, что вершина и одна из сторон этих углов совпадают, то первый угол меньше второго. Назовём прилежащими два угла, расположенные так, что сторона одного совпадает со стороной другого (а значит, совпадают и вершины), но их внутренние области не пересекаются. Угол, составленный из несовпадающих сторон двух прилежащих углов, назовём сложенным из этих углов. Каждому углу можно поставить в соответствие число (угловую меру) таким образом, что:
- равным углам соответствует равная угловая мера;
- меньшему углу соответствует меньшая угловая мера;
- у угла, стороны которого совпадают (нулевого угла), угловая мера равна нулю (то же справедливо и для угла между параллельными прямыми);
- каждый ненулевой угол имеет определённую угловую меру, большую нуля;
- (аддитивность) угловая мера угла равна сумме угловых мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
В некоторых системах обозначений, если есть необходимость различать угол и его меру, для угла (геометрической фигуры) используют обозначение 


Мера угла
θ в радианах равна отношению длины стягивающей его дуги
s к её радиусу
r
Угол измеряют:
- в градусах, минутах, секундах;
- в радианах;
- в оборотах;
- в градах, минутах, секундах;
- в часах, минутах и секундах;
- в тысячных и делениях угломера;
- в румбах.
Наиболее распространённая градусная мера — градус, минута, секунда, в которой за 1° принимается 1/180 от развёрнутого угла (см. ниже), одна минута 


Радианная мера угла — отношение длины s стягивающей дуги к её радиусу r. Радианная мера используется в математическом анализе (например, как числовой аргумент тригонометрических функций и при определении числовых (табличных и графических) значений обратных аркфункций), в планиметрии и механике (при рассмотрении вращения около точки или оси и других процессов, описываемых с помощью тригонометрических функций, — колебаний, волн и так далее).
Углы можно измерять также в оборотах. Один оборот — это полный угол (то есть угол в 360 градусов). Про произвольный угол говорят, что он составляет x оборотов, если x — отношение длины s дуги, стягивающей угол, к длине L окружности, содержащей эту дугу.
Градовая мера измерения углов была предложена к применению исторически, в настоящее время почти нигде не используется, поскольку не вытеснила более распространённую шестидесятеричную градусную.
Измерение углов в градусной мере восходит к Древнему Вавилону, где использовалась шестидесятеричная система счисления, следы которой сохранились у нас в делении времени и углов. Один градус (1/360 полного угла) делится на 60 угловых минут (или минут дуги), в свою очередь минута делится на 60 угловых секунд (секунд дуги). Меньшие углы измеряются в дольных единицах секунды, образуемыми с помощью приставок СИ (угловая миллисекунда, угловая микросекунда и т.д.).
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ основной единицей измерения угла является радиан.

В морской терминологии углы измеряются в румбах. 1 румб равен 1⁄32 от полной окружности (360 градусов) компаса, то есть 11,25 градуса, или 11°15′.
В астрономии угол прямого восхождения и часовой угол в экваториальной системе координат измеряются в часах, минутах и секундах (составляющих соответственно 1⁄24, 1⁄1440 и 1⁄86 400 полной окружности); это связано с угловой скоростью осевого вращения Земли, составляющей приблизительно 1 оборот за 24 часа[2]. Таким образом, за один час (минуту, секунду) времени небесная сфера «поворачивается» примерно на 1 час (минуту, секунду) в угловой мере. Остальные угловые величины в астрономии выражаются обычно в градусах, минутах и секундах дуги. Одна секунда (минута) прямого восхождения равна 15 секундам (минутам) дуги.
В артиллерии и оружейном деле используются также тысячные и деления угломера.
В некоторых контекстах, таких как идентификация точки в полярных координатах или описание ориентации объекта в двух измерениях относительно его базовой ориентации, углы, отличающиеся на целое число полных оборотов, фактически являются эквивалентными. Например, в таких случаях можно считать эквивалентными углы 15° и 360015° (= 15° + 360°×1000). В других контекстах, таких как идентификация точки на спиральной кривой или описание совокупного вращения объекта в двух измерениях относительно его начальной ориентации, углы, отличающиеся на ненулевое целое число полных оборотов, не эквивалентны.
Некоторые плоские углы имеют специальные названия. Кроме вышеназванных единиц измерения (радиан, румб, градус и тому подобное), к ним относятся:
- квадрант (прямой угол, 1⁄4 окружности);
- секстант (1⁄6 окружности);
- октант (1⁄8 окружности; кроме того, в стереометрии октантом называется трёхгранный угол, образованный тремя взаимно перпендикулярными плоскостями),

Обозначение угла уклона дороги на дорожном знаке
Иногда углы (например, угол уклона поверхности) измеряют не собственно угловой мерой, а её тангенсом (или синусом), то есть отношением подъёма по наклонной плоскости к проекции на горизонталь пройденного по ней пути (или к самому этому пути). Для обычного случая малых углов уклона это отношение примерно равно углу, выраженному в радианах (tg α ≈ sin α ≈ α, при α < 0,1 разница между этими величинами менее 1 %). При этом отношение выражается обычно в процентах или промилле. Например, уклон дороги в 10 % означает, что на каждые 100 метров пути (в проекции на горизонталь) дорога поднимается на 10 м; угол к горизонту равен arctg(10/100) ≈ 5,71° ≈ 0,1 радиана.
Такой способ измерения углов не является, строго говоря, угловой мерой, так как не обладает свойством аддитивности (см. выше).
См. также приближения для малых углов[en].
Направление отсчёта углов[править | править код]

Стрелкой показано направление отсчёта углов
В математике и физике, обычно, положительным направлением отсчёта углов считается направление против часовой стрелки. Обычно, угол начинают измерять от луча, начало которого совпадает с центром системы координат (СК), а направление совпадает с положительным направлением оси абсцисс (в полярной СК, цилиндрической СК, сферической СК, СК на тригонометрической окружности и других).
В географии и геодезии за начало отсчёта углов по азимуту принято направление «на север»; угол отсчитывается по часовой стрелке.
Таким образом, направлению «на восток» соответствует азимутальный угол 90°, «на юг» — 180°, «на запад» — 270°. В артиллерии предпочитают направление полярной оси «на юг» и соответствующий полярный угол называют также азимутом (направление «на запад» соответствует азимутальному углу 90°).
Типы углов[править | править код]
-
Выпуклый угол
-
Прямой угол
-

Полный угол
-

Острый угол
-

Тупой угол
-
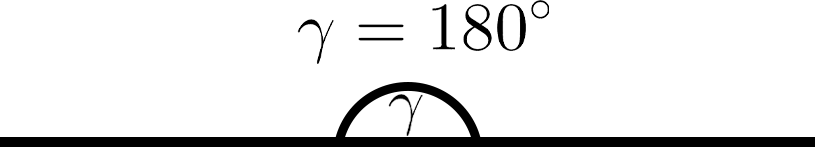
Развёрнутый угол
В зависимости от величины углы называются следующим образом.
- Нулевой угол (0°); стороны нулевого угла совпадают, его внутренняя область — пустое множество.
- Острый угол (от 0° до 90°, не включая граничные значения).
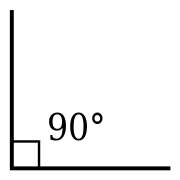
- Прямой угол (90°); стороны прямого угла перпендикулярны друг другу.
- Тупой угол (от 90° до 180°, не включая граничные значения).
- Косой угол (любой, не равный 0°, 90°, 180° или 270°).
- Развёрнутый угол (180°); сторонами развёрнутого угла являются две полупрямые одной прямой, то есть два луча, направленных в противоположные стороны.
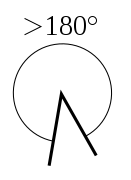
- Невыпуклый угол (от 0° до 180° включительно).
- Выпуклый угол (от 180° до 360°, не включая граничные значения).
- Полный угол (360°) — см. оборот (единица измерения).
Биссектриса[править | править код]
Биссектрисой (от лат. bi- «двойное» и sectio «разрезание») угла называется луч, выходящий из вершины угла и проходящий через его внутреннюю область, который образует с его сторонами два равных угла. Расстояние любой точки биссектрисы от сторон угла одинаково (и, обратно, любая точка внутренней области угла, равноудалённая от сторон угла, лежит на его биссектрисе).
Плоские углы[править | править код]
Термин плоский угол употребляется как синоним термина угол, определённого в начале статьи, для отличия его от употребляемого в стереометрии понятия телесного угла (в том числе двугранного, трёхгранного или многогранного угла).
Под свойствами плоских углов нередко понимают соотношения величин углов (смежных, дополнительных, прилегающих, вертикальных — см. ниже) в случае, когда углы лежат в одной плоскости (для планиметрии это подразумевается само собой, однако для стереометрии уточнение необходимо, иначе перечисленные ниже соотношения не имеют места, а сами углы, если не лежат в одной плоскости, не называются смежными или прилегающими (вертикальные всегда лежат в одной плоскости автоматически).
Вертикальные и прилежащие углы[править | править код]
-

Вертикальные углы. Две пары углов (A и B, C и D) попарно равны
-
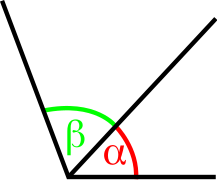
Прилежащие углы. Величина угла, образованного внешними (не общими) их сторонами, равна сумме величин их самих (α + β)
-

Дополнительные углы a и b (взаимно дополняют друг друга до прямого угла). Оба дополнительных угла являются острыми
-
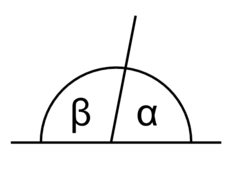
Смежные углы — на этом рисунке острый (α) и тупой (β) — образуют развёрнутый угол (α + β)
-
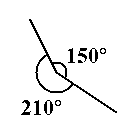
Сопряжённые углы — образуют полный угол (360°); на этом рисунке частный пример: 150° + 210° = 360°
- Вертикальные углы — два угла на плоскости, которые образуются при пересечении двух прямых и не имеющие общих сторон (стороны одного угла являются продолжением сторон другого). Их основное свойство: вертикальные углы равны.
- Прилежащие углы — два угла на плоскости, имеющие общими по одной вершине и по одной из двух сторон, но не пересекающиеся внутренними областями. Величина угла, образованного двумя внешними (не общими) сторонами прилежащих углов, равна сумме величин самих прилежащих углов (на рисунке α + β).
Частные случаи прилежащих углов.
- Если прилежащие углы равны, то их общая сторона — биссектриса.объединённого угла.
- Дополнительные углы — два угла с общей вершиной на плоскости, одна из сторон которых — общая, а оставшиеся стороны составляют прямой угол. Сумма дополнительных углов равна 90°. Синус, тангенс и секанс угла равны соответственно косинусу, котангенсу и косекансу дополнительного угла.
- Смежные углы — два угла с общей вершиной на плоскости, одна из двух сторон которых общая, а оставшиеся две стороны лежат на одной прямой (не совпадая). Сумма двух смежных углов равна 180°. То есть два смежных угла на плоскости — это два прилежащих угла, дающих в сумме 180°.
- Сопряжённые углы — два угла на плоскости, имеющие общими одну вершину и две стороны, по которым они примыкают (граничат) друг к другу, но различаются внутренними областями; объединение таких двух углов представляет собой всю плоскость, а, как прилежащие углы, они образуют в сумме полный угол; сумма их величин равна 360°.
Плоские углы с (анти)параллельными сторонами[править | править код]

Углы с параллельными сторонами.
Углы, стороны которых попарно параллельны и сонаправлены (или попарно параллельны и противоположно направлены), равны друг другу. Пара углов, у которых одна пара сторон параллельна и сонаправлена друг другу, а вторая пара сторон параллельна и противоположно направлена, составляют в сумме по величине развёрнутый угол, то 180° (см. рисунок) — поскольку их можно параллельным переносом превратить в смежные углы («склеив» сонаправленные стороны).
Углы со взаимно перпендикулярными сторонами[править | править код]
- Два угла со взаимно перпендикулярными сторонами равны, если оба они острые или оба тупые.
Внешний угол треугольника[править | править код]
- Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с внешним углом.
Углы многоугольника[править | править код]
Сумма внутренних углов αi произвольного n-угольника без самопересечений равна 
Так,
- сумма внутренних углов треугольника равна 180°,
- четырёхугольника — 360°,
- пятиугольника — 540° и так далее.
Следствие[править | править код]
Назовём внешним углом βi (внимание, это не обычное определение внешнего угла) угол, дополняющий внутренний угол αi до полного угла: βi = 360° − αi.
Сумма внешних углов произвольного n-угольника без самопересечений равна 
Центральный и вписанный угол[править | править код]
Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.
-
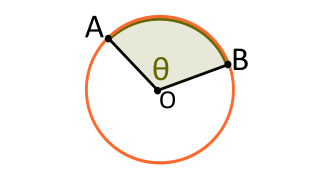
Центральный угол
-

Вписанный угол
- Центральный угол — угол с вершиной в центре окружности. Величина центрального угла равна градусной мере дуги, заключённой между сторонами этого угла.
- Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Величина вписанного угла равна половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол θ равен половине величины центрального угла 2θ, , опирающегося у основания на окружности на ту же самую дугу (розового цвета). То есть угол θ не меняет своей величины от вершины к вершине, взятой на окружности (зелёный и голубой углы). Внешний угол для вписанного с другой стороны угла окружности имеет ту же величину θ (коричневого цвета)
Величина вписанного угла равна половине величины центрального угла, опирающегося у основания на окружности на ту же самую дугу (см. рис.).
Вариации и обобщения[править | править код]
Величиной ориентированного угла между прямыми 








б) 


Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла, расширив его область определения на всю числовую прямую 
Понятие угла обобщается на рассматриваемый в стереометрии телесный угол.
Телесный угол[править | править код]
Обобщением плоского угла на стереометрию является телесный угол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол).
Телесные углы измеряются в стерадианах (одна из основных единиц СИ), а также во внесистемных единицах — в частях полной сферы (то есть полного телесного угла, составляющего 4π стерадиан), в квадратных градусах, квадратных минутах и квадратных секундах.
Телесными углами являются, в частности, следующие геометрические тела:
- двугранный угол — часть пространства, ограниченная двумя пересекающимися плоскостями;
- трёхгранный угол — часть пространства, ограниченная тремя пересекающимися плоскостями;
- многогранный угол — часть пространства, ограниченная несколькими плоскостями, пересекающимися в одной точке.
Двугранный угол может характеризоваться как линейным углом (углом между образующими его плоскостями), так и телесным углом (в качестве вершины может быть выбрана любая точка на его ребре — прямой пересечения его граней). Если линейный угол двугранного угла (в радианах) равен φ, то его телесный угол (в стерадианах) равен 2φ.
Угол между кривыми[править | править код]

Угол между двумя кривыми в точке Р определяется как угол между касательными А и В в P.
Как в планиметрии, так и в стереометрии, а также в ряде других геометрий можно определить угол между гладкими кривыми в точке пересечения: по определению, его величина равна величине угла между касательными к кривым в точке пересечения.
Угол и скалярное произведение[править | править код]
Понятие угла можно определить для линейных пространств произвольной природы (и произвольной, в том числе бесконечной размерности), на которых аксиоматически введено положительно определённое скалярное произведение 








В частности, можно ввести понятие угла между непрерывными на некотором интервале ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


В римановой геометрии можно аналогично определить угол между касательными векторами с помощью метрического тензора 






Угол в метрическом пространстве[править | править код]
Также существует ряд работ, в которых вводится понятие угла между элементами метрического пространства.
Пусть 

К. Менгер ввёл понятие угла между вершинами 



В 1932 году Вильсон рассмотрел в качестве угла следующее выражение:

Нетрудно видеть, что введённое выражение всегда имеет смысл и удовлетворяет трём аксиомам Менгера.
Кроме того, угол Вильсона обладает тем свойством, что в евклидовом пространстве он эквивалентен углу между элементами 

Измерение углов[править | править код]
Одним из самых распространённых инструментов для построения и измерения углов является транспортир (а также линейка — см. ниже); как правило, он используется для построения угла определённой величины. Для более или менее точного измерения углов разработано много инструментов:
- угломер;
- гониометр — прибор для лабораторного измерения углов;
- кипрегель — геодезический угломерный инструмент.
Угловым расстоянием (или просто углом) между двумя объектами для наблюдателя называется мера угла, в вершине которого находится наблюдатель, а объекты лежат на сторонах. Для грубой оценки углов между двумя удалёнными предметами можно использовать кисть руки. На расстоянии вытянутой руки угловому расстоянию в 1 градус (1°) соответствует ширина мизинца (см. также ниже; угловая ширина среднего пальца на расстоянии вытянутой руки составляет около 2°), углу в 10 градусов — ширина сжатого кулака, расположенного горизонтально (либо поперечник ладони), углу в 20 градусов (или около 15°÷17°÷20°) — расстояние между кончиками разведённых большого и указательного пальца (пядь), а угловое расстояние от конца мизинца до конца большого пальца равно примерно четверти прямого угла. Это усреднённые данные. Рекомендуется уточнить их для своей собственной руки.
Различные методы и устройства для измерения углов характеризуются угловым разрешением, то есть минимальным углом, который может быть измерен с помощью данного метода. Наилучшим угловым разрешением обладают различные интерферометрические методы, позволяющие измерить в некоторых случаях углы в несколько микросекунд дуги (~10−11 радиана).
Примеры практических тригонометрических измерений[править | править код]
- Решение задач простым способом
Как измерить угол (например, на карте) с помощью сторон треугольника (например, при отсутствии инженерного/тригонометрического калькулятора (и таблиц) и отсутствии ПК (MS Office Excel) для вычисления cos) и подручными средствами — линейки с миллиметровыми делениями?
По сторонам угла отложите отрезки по 60 мм и концы соедините прямой линией. Длина этой линии в миллиметрах покажет примерно величину угла в градусах. Таким способом можно с достаточной (приемлемой) точностью измерять острые углы до 60°. Если угол больше 60°, измеряют его дополнение до 90°, 180, 270° или 360°. Для измерения дополнения до 90° или 270° из вершины угла строится с помощью треугольника перпендикуляр к одной из сторон (в равнобедренном треугольнике — медиана-биссектриса, она же является высотой).
Как измерить угол линейкой (при визуальном ориентировании на местности …и сравнить угол по карте — см. пункт 1)?
Поместите линейку с миллиметровыми делениями перед собой на расстоянии 57 см (не более 60 см) от глаза. В этом случае деление, равное 1 см, будет соответствовать углу визирования в 1°. В справедливости данного способа вы легко убедитесь, если помните, что дуга центрального угла в 1° составляет примерно 1/57 часть радиуса. Точность измерения углов с помощью линейки (также как и с помощью пальцев; см. ниже) зависит от точности положения линейки (или пальцев) на необходимом расстоянии от глаза. В этом можно быстро натренироваться с помощью нитки, длина которой соответствует расстоянию от глаза до пальцев вытянутой руки.
Как можно измерять и откладывать на местности углы без применения угломерных приборов?
Наиболее просто это можно сделать сравнением измеряемого угла с прямым. Прямой угол вы можете отложить направлениями рук, одна из которых вытянута вдоль плеч, а вторая с поднятым большим пальцем направлена так, чтобы палец правой руки был перед правым глазом (соответственно палец левой руки — перед левым глазом). Прямой угол можно глазомерно поделить на две или три равные части, каждая из которых будет соответствовать 45° или 30°.
Меньшие значения углов можно отложить или измерить на местности следующим приёмом. Прежде всего измерьте линейкой ширину трёх сомкнутых пальцев своей руки: указательного, среднего и безымянного. Если она у вас будет равна 6 см, то при вытянутой на 60 см руке угол визирования на них составит примерно 6°. Соответственно угол визирования на каждый из этих трёх пальцев будет равен в среднем 2°. Если же ширина трёх пальцев получится у вас, например, 5 см, то, чтобы углы визирования были такими же, руку надо вытягивать на 50 см.
При вытянутой руке угол визирования на большой и указательный пальцы, раздвинутые под прямым углом, составляет примерно 15°. Как это проверить и уточнить?
Прежде всего заметьте на местности ориентир и от него отложите угол 90°. Это можно сделать приёмом, описанным в предыдущей задаче. Затем от ориентира отложите шесть углов по 15° визированием на большой и указательный пальцы, раздвинутые под прямым углом. Последнее отложение угла должно составить на местности прямой угол. Если этого точно не получилось, нужно повторить отложения, держа вытянутую руку немного ближе или дальше от глаза (порядка 60 см). Этим самым вы определите расстояние, на которое нужно вытягивать руку для отложения угла 15°[3].
Углы также можно вычислить (рассчитать) с помощью различных измерительных приборов и приспособлений — посредством тригонометрии на счётной линейке, инженерном калькуляторе (в том числе калькулятор (Windows)), с помощью функций таблицы MS Office Excel: (1) cos, (2) затем arccos, и (3) перевести, также функциями, значение радианов в градусы (°) (при наличии ПК; существуют и on-line-вычисление углов треугольника по заданным сторонам);
Существуют также специальные тригонометрические таблицы: sin, cos, а также arccos, arcsin, последние, кстати, могут быть (в том числе и чаще всего) с перерасчётом в градусы.
В аналитической геометрии угол между прямыми в координатной плоскости, например, задаётся уравнением:
(см. Линейная функция; см. также #Угол и скалярное произведение)
Примечания[править | править код]
- ↑ Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467—468. — 1248 стб. : ил. — 150 000 экз.
- ↑ В действительности истинный период обращения Земли относительно неподвижных звёзд примерно на 4 минуты короче, чем 24 часа, см. звёздное время.
- ↑ Куприн А. М. На местности и по карте. — М. Недра, 1982. — 112 с.
См. также[править | править код]
- Азимут (астрономия)
- Азимут (геодезия)
- Антипараллельные прямые
- Апертурный угол
- Астрономическая рефракция
- Двугранный угол
- Дирекционный угол
- Изогона
- Кастор (угол)
- Магнитный азимут
- Многоугольник
- Наклон, уклон
- Ортогональность
- Параллельные прямые
- Угол поворота
- Позиционный угол и Угловое расстояние (Полярные координаты)
- Полигонометрия
- Решение треугольников
- Румб
- Сингония
- Склонение (астрономия) и Часовой угол (Системы небесных координат)
- Телесный угол
- Трёхгранный угол
- Триангуляция
- Тригонометрический параллакс & Параллактический угол
- Тригонометрия
- Угловая скорость (& CAV)
- Угловая частота
- Угловое разрешение
- Угловое ускорение
- Угловой коэффициент (Линейная функция)
- Угловой размер
- Углы Эйлера
- Угол места
- Угол обзора
- Угол поля зрения объектива
- Угол скольжения
- Категория:Углы
Литература[править | править код]
- Барабанов О. О. Начала истории прямого угла // История науки и техники. — 2015. — № 1. — С. 16—27.‘
- Погорелов А. В. Геометрия: учебник для 7—11 классов средней школы. — М.: Просвещение, 1992. — 383 с. — ISBN 9785090038546.
- Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467‒468. — 1248 стб. : ил. — 150 000 экз.
- Двугранный угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1979. — Т. 2: Д — Коо. — Стб. 50. — 1104 стб. : ил. — 150 000 экз.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30‒31. — ISBN 5-94057-170-0.
- Угломерные приборы/Угол (плоский) // Большая Советская энциклопедия (в 30 т.) / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская Энциклопедия», 1977. — Т. XXVI. — С. 459‒460. — 624 с.
- Weisstein, Eric W. Line Bisector (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Angle (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Polygon (англ.) на сайте Wolfram MathWorld.
- K. Menger. New Fondations of Euclidean Geometry (англ.) // THE AMERICAN JOURNAL OF MATHEMATICS 53 : журнал. — 1931. — P. 721‒745.
- W. A. Wilson. On angles in certain metric spaces (англ.) // Bulletin of American Mathematical Society 39. — 1932. — P. 580‒588.

