Если у вас нет времени на выполнение заданий по чертежам, вы всегда можете попросить меня, пришлите задания мне в  whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.
whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.

 Ответы на вопросы по заказу чертежей:
Ответы на вопросы по заказу чертежей:

 Сколько стоит помощь?
Сколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам – я изучу и оценю.
 Какой срок выполнения?
Какой срок выполнения?
- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
 Если требуется доработка, это бесплатно?
Если требуется доработка, это бесплатно?
- Доработка бесплатна. Срок выполнения от 1 до 2 дней.
 Могу ли я не платить, если меня не устроит стоимость?
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости бесплатна.
 Каким способом можно оплатить?
Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.
 Какие у вас гарантии?
Какие у вас гарантии?
- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.
 В какое время я вам могу написать и прислать задание на выполнение?
В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время! Я стараюсь быть всегда онлайн.

 Ниже размещён теоретический и практический материал, который вам поможет разобраться с “Чертежами”, если у вас есть желание и много свободного времени!
Ниже размещён теоретический и практический материал, который вам поможет разобраться с “Чертежами”, если у вас есть желание и много свободного времени!

Содержание:
- Ответы на вопросы по заказу чертежей:
- Тема 1. Точка и прямая линия
- Пример задачи 1
- Варианты задания № 1
- Тема 2. Поверхности
- Пример задачи 2
- Пример задачи 3
- Пример задачи 4
- Варианты задания № 2
- Тема 3. Преобразование чертежа
- Пример задачи 5
- Пример задачи 6
- Варианты задания № 3
- Тема 4. Сечение поверхности плоскостью
- Пример задачи 7
- Пример задачи 8
- Варианты задания № 4
- Тема 5. Пересечение поверхностей
- Пример задачи 9
- Пример задачи 10
- Варианты задания № 5
- Тема 6. Развертки технических форм
- Пример задачи 11
- Пример задачи 12
- Варианты задания № 6
- Оформление индивидуальных графических заданий
Тема 1. Точка и прямая линия
Цель – закрепить знания о свойствах параллельного прямоугольного проецирования, выработать навыки решения задач на определение взаимного положения точек и прямых в прямоугольных проекциях.
Для выполнения заданий по данной теме следует вспомнить следующие теоретические положения:
- При параллельном проецировании проекции параллельных прямых параллельны, сохраняется отношение длин отрезков.
- Если стороны угла не параллельны плоскости проекции, то угол проецируется на эту плоскость с искажениями. Для проецирования прямого угла ортогонально без искажения на плоскость проекций необходимо и достаточно, чтобы по крайней мере одна его сторона была параллельна, а вторая неперпендикулярна этой плоскости.
- Прямые, перпендикулярные или параллельные плоскости проекций, называются прямыми частного положения. Если прямая параллельна горизонтальной, фронтальной или профильной плоскости проекций, то она называется горизонталью, фронталью или профилью соответственно.
Если прямая перпендикулярна к горизонтальной, фронтальной или профильной плоскости проекций, то она называется горизонтально-, фронтально-, профильно-проецирующей прямой соответственно.
Если прямая перпендикулярна плоскости проекций, то на эту плоскость она проецируется в истинную величину.
Истинную величину отрезка прямой общего положения и угол ее наклона к плоскости проекций можно определить методом прямоугольного треугольника, суть которого в том, что для графического определения на чертеже действительной величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную) проекцию отрезка, а за другой – разность удаления концов отрезка от горизонтальной (фронтальной) плоскости проекций. Искомый угол лежит в прямоугольном треугольнике напротив катета, представляющего разность удаления концов отрезка от плоскости проекций.
Рассмотренные положения помогут в построении на чертеже различных геометрических образов, применяемых в инженерном деле, в частности в решении задач, связанных со стержневыми конструкциями (фермами). Методы начертательной геометрии применяются как при конструктивном оформлении ферм, подъемно-транспортной техники, так и при определении усилий в их элементах. Мосты, подъемные краны, буровые вышки, мачты высоковольтных линий и т.д. -пространственные стержневые конструкции. Стальные стержни различных профилей соединяются сваркой и клепкой. Несколько сходящихся стержней образуют узел. Комплексные чертежи сложных конструкций иногда дополняются для облегчения сборки наглядными изображениями (аксонометрическими проекциями), которые также строятся по правилам, изучаемым в начертательной геометрии. Для технических расчетов стержневые конструкции вычерчиваются упрощенно: каждый стержень изображается отрезком прямой. Расчеты ферм, в конечном счете, сводятся к задачам на сложение и разложение усилий – пространственных векторов. В этом случае, если имеют дело с системами, имеющими большое количество узлов, вырезают из фермы последовательно отдельные узлы и рассматривают усилия в стержнях каждого узла. Задачи такого рода рассматриваются (с применением графических методов) в курсах теоретической и строительной механики.
Прежде чем обратиться к примеру, рассмотрим последовательность решения всех заданий.
- Анализ данных. По указанным проекциям геометрических образов, составляющих исходные данные задания, представляют их форму и взаимное расположение в пространстве как по отношению друг к другу, так и относительно плоскостей проекций.
- Анализ решения. На этом этапе намечается «пространственный» план решения задач, устанавливается последовательность геометрических операций, при помощи которых может быть получен ответ на поставленную задачу, и выбирается оптимальный ход решения.
- Запись алгоритма выбранного решения.
- Геометрические построения – реализация на чертеже составленного плана решения задачи в пространстве с помощью инструмента.
- Следует иметь в виду, что в ряде случаев некоторые этапы могут отсутствовать.
Пример задачи 1
Построить ортогональные проекции элемента AEHD фермы (рис. 1), если дано: три проекции стержня EH; фронтальная проекция высоты равнобокой трапеции AEHD лежит на a; высота трапеции равна 1,5EH; AE = 2EH.
Анализ данных. Отрезок EH – горизонталь, следовательно, E’H’ – истинная величина EH. Прямая a  EH; EH // AD.
EH; EH // AD.
Анализ решения. Располагаем ли мы достаточной информацией для того, чтобы построить проекции высоты AEDH? Да. Нам известно, что a  EH, следовательно, a’
EH, следовательно, a’  E’H’. Нам известна истинная величина высоты. Воспользовавшись способом прямоугольного треугольника и тем обстоятельством, что |EH|= E’H’, мы можем построить проекции высоты.
E’H’. Нам известна истинная величина высоты. Воспользовавшись способом прямоугольного треугольника и тем обстоятельством, что |EH|= E’H’, мы можем построить проекции высоты.
Можем ли мы теперь построить проекции большого основания трапеции? Да, так как мы знаем, что EH // AD, истинные величины высоты и боковой стороны трапеции.
Алгоритм решения (рис. 2).
1. Проводим горизонтальную проекцию прямой a’  E’H’, а’ принадлежит E’.
E’H’, а’ принадлежит E’.
2. Берем произвольную точку на прямой a -(•)1 (•)1 принадлежит a.
3. Находим истинную величину [E -1]. Для этого строим прямоугольный треугольник E’1′K, у которого 1′K =  (1 – E); E’K = (E -1).
(1 – E); E’K = (E -1).

4. Находим проекции высоты. Для этого откладываем на продолжении E’K отрезок E’M = 1,5EH = 1,5 E’H’. Проводим [M – 2] // [K -1], [E – 2] – высота трапеции.
5. Находим величину отрезка A – 2. Для этого на свободном поле чертежа проводим m  n (рис. 3). Точка 2 принадлежит m; 2 – E = EM. Из точки E проводим окружность радиусом R = 2E’H’ до пересечения m в точке A. Отрезок A – 2 искомый.
n (рис. 3). Точка 2 принадлежит m; 2 – E = EM. Из точки E проводим окружность радиусом R = 2E’H’ до пересечения m в точке A. Отрезок A – 2 искомый.
6. Строим проекции основания трапеции. Так как AD // EH , то через точку 2′ проведем l‘ // E’H’; l‘ принадлежит 2′ и отложим от точки 2’ отрезок A‘ – 2’ = A – 2 .
Аналогично найдем точку D‘, используя линии связи A” и D.

Рис. 3
Возможно, вас также заинтересует эта ссылка:
Варианты задания № 1
Варианты 1-5. Построить ортогональные проекции элемента ESF фермы. Дано: проекции стержня EF, треугольник ESF равносторонний, высота треугольника ESF лежит на прямой a . Определить углы наклона стержня ES к плоскостям проекций.
Варианты 6-10. Построить ортогональные проекции элемента ASD фермы. Дано: проекции стержня EF, треугольник ASD равнобедренный, высота треугольника ASD лежит на прямой a и ее истинная величина равна 2EF, стержень EF делит высоту на две равные части. Определить периметр элемента ASD .
Варианты 11-20. Построить ортогональные проекции элемента ABCD фермы. Дано: ABCD – ромб, проекции стержня BD, стержень AC лежит на прямой a , DC = 0,8BD .
Варианты 21-24. Построить ортогональные проекции элемента ABCD фермы. Дано: ABCD – квадрат, диагональ BD лежит на прямой l, вершина A – на прямой m, K – точка пересечения диагоналей. Определить углы наклона AC к плоскостям проекций.






Возможно, вас также заинтересует эта ссылка:
Тема 2. Поверхности
Цель – проверить знания по разделу «Изображение в прямоугольных проекциях каркасов и очерков поверхностей, точек и линий, принадлежащих этим поверхностям».
Для успешной работы по этому заданию следует восстановить в памяти следующие теоретические сведения.
1. Линейным каркасом называется множество линий, имеющих единый закон образования и связанных между собой определенной зависимостью.
2. Под определителем поверхности понимают совокупность независимых условий, однозначно задающих поверхность. В число этих условий должны быть включены:
• геометрические фигуры (точки, линии, поверхности), с помощью которых может быть образована поверхность – геометрическая часть определителя – (Г) .
• алгоритм образования поверхности из геометрических фигур, включенных в состав геометрической части определителя, т.е. сведения о законе ее перемещения и характере изменения формы производящей [A, A1 ]. Определитель любой поверхности можно представить в виде Ф(Г)[A, A1 ], где A – закон перемещения; A1 – закон изменения формы.
3. Очерком данной поверхности называют линию пересечения с плоскостью проекций проецирующей поверхности, обертывающей данную поверхность.
4. Построение линий и точек, принадлежащих поверхности, производится с помощью каркаса поверхности. Точка принадлежит поверхности, если она находится на линии этой поверхности.
Каркасные поверхности широко используются на практике. Например, поверхность зуба цилиндрического зубчатого колеса – цилиндрическая поверхность, определитель которой  , где
, где  – прямолинейная образующая,
– прямолинейная образующая,  – криволинейная направляющая. Для создания переходных участков между двумя поверхностями типа трубопроводов, имеющих различную форму, но одинаковую площадь нормального сечения, одинаковую форму, но различные площади сечения, различную форму и различные формы поперечных сечений, служит каналовая поверхность Ф(
– криволинейная направляющая. Для создания переходных участков между двумя поверхностями типа трубопроводов, имеющих различную форму, но одинаковую площадь нормального сечения, одинаковую форму, но различные площади сечения, различную форму и различные формы поперечных сечений, служит каналовая поверхность Ф( )[A, A1], где
)[A, A1], где  – криволинейная производящая,
– криволинейная производящая,  – криволинейная направляющая.
– криволинейная направляющая.
Поверхность косого клина с определителем  используется при конструировании поверхности крыла летательного аппарата. Поверхность однополосного гиперболоида вращения используется в строительном деле для передачи вращения с помощью зубчатых или фрикционных гиперболоидных колес при скрещивающихся осях. Косая плоскость
используется при конструировании поверхности крыла летательного аппарата. Поверхность однополосного гиперболоида вращения используется в строительном деле для передачи вращения с помощью зубчатых или фрикционных гиперболоидных колес при скрещивающихся осях. Косая плоскость  [A] применяется в инженерно-строительной практике для формирования поверхностей откосов, насыпей, железных и автомобильных дорог, набережных, гидротехнических сооружений в местах сопряжения откосов, имеющих различные углы наклона. Широко используемые в технике сферические, тороидальные, глобоидные, эллипсоидные, параболические, гиперболические поверхности – поверхности вращения, определитель которых
[A] применяется в инженерно-строительной практике для формирования поверхностей откосов, насыпей, железных и автомобильных дорог, набережных, гидротехнических сооружений в местах сопряжения откосов, имеющих различные углы наклона. Широко используемые в технике сферические, тороидальные, глобоидные, эллипсоидные, параболические, гиперболические поверхности – поверхности вращения, определитель которых  [A]. Общеизвестно значение и широкое применение винтовых поверхностей, определитель
[A]. Общеизвестно значение и широкое применение винтовых поверхностей, определитель  [A], в технике (крепежные изделия, домкраты, ходовые винты станков, судовые, самолетные и вентиляторные винты, червяки, сверла, винты транспортеров – шнеки и т.д.).
[A], в технике (крепежные изделия, домкраты, ходовые винты станков, судовые, самолетные и вентиляторные винты, червяки, сверла, винты транспортеров – шнеки и т.д.).
Рассмотрим более подробно использование косого клина на практике. Косым клином называется поверхность, которая образуется перемещением прямолинейной производящей по трем направляющим, расположенным в параллельных плоскостях, причем две направляющие – гладкие кривые, а третья – прямая линия. Прием конструирования линейчатой поверхности с пропорциональным делением хорд применяется при построении технической поверхности крыла летательного аппарата (рис. 4). Форма кривых m и n, являющихся направляющими поверхностями, позволяет строить в каждой из этих кривых единственные хорды соприкосновения AB и CD при большом диапазоне выбора направления проецирования S . Поверхность – косой клин – дает технологические преимущества при изготовлении каркаса и лучше удовлетворяет аэродинамическим требованиям. Наличие третьей прямолинейной направляющей дает возможность простого построения чертежа каркаса поверхности при проецировании на плоскость, перпендикулярную направлению S. Любая плоскость  , проходящая через направляющую l, делит хорды соприкосновения AB и CD, опирающиеся на плоскости
, проходящая через направляющую l, делит хорды соприкосновения AB и CD, опирающиеся на плоскости  и
и  , в одном и том же отношении.
, в одном и том же отношении.
 Рис. 4
Рис. 4
Рассмотрим пример построения на комплексном чертеже каркаса крыла (рис. 5). Поверхность – косой клин – задана тремя направляющими: m , n криволинейные, и l прямая. Все три направляющие расположены в параллельных плоскостях. Кроме построения каркаса, требуется по заданной фронтальной проекции K” найти горизонтальную проекцию K’ линии K , лежащей на поверхности, и фронтальную проекцию точки E – E” , также лежащей на поверхности косого клина, по заданной горизонтальной проекции E’.

Рис. 5
Анализ данных. Поверхность задана полно, однозначно.
Анализ решения. Располагаем ли мы достаточными данными для построения поверхности? Да. Форма кривых m и n позволяет строить в каждой из этих кривых единственные хорды AB и CD, причем их горизонтальные проекции совпадают с горизонтальными проекциями кривых m и n. Если мы одну из хорд соприкосновения разделим на части и проведем через точки деления плоскость, проходящую через l, то и вторая хорда будет разделена на части в том же соотношении. Разделив хорды, мы найдем соответствующие делению точки на направляющих и, соединив их, построим каркас поверхности.
Располагаем ли мы данными для построения недостающих проекций точки и линий, принадлежащих поверхности? Да. Недостающие проекции мы найдем, если воспользуемся условием принадлежности: точка принадлежит поверхности, если она принадлежит прямой, лежащей на поверхности. Линия принадлежит поверхности, если она проходит через точки, лежащие на поверхности.
Алгоритм решения:
- Делим горизонтальную проекцию хорды AB на четыре части.
- Соединяем точки 1′, 2′, 3′, 4’с точкой l‘.
- Находим фронтальные проекции точек 1 – 6.
- Находим соответствующие пропорциональному делению хорд точки на направляющих m и n, не давая им обозначение, чтобы не загромождать чертеж.
- Строим проекции каркаса поверхности.
- Строим горизонтальную проекцию линии K, для чего найдем горизонтальные проекции точек 7 -10 (зная, что эти точки лежат на линиях каркаса а7; a8; a9; a10) и соединим их.
- Строим фронтальную проекцию E” точки E , проведя для этого линию каркаса aE.
Пример задачи 2
Построить каркас оболочки, которая задана двумя направляющим  , [AB] и плоскостью параллелизма
, [AB] и плоскостью параллелизма  . Производящая a – прямая. Построить горизонтальную проекцию A’ точки A, лежащей на поверхности оболочки (рис. 6), по заданной фронтальной проекции A”.
. Производящая a – прямая. Построить горизонтальную проекцию A’ точки A, лежащей на поверхности оболочки (рис. 6), по заданной фронтальной проекции A”.
 Рис 1.6
Рис 1.6
Анализ данных. Поверхность задана полно. По определителю можно сказать, что это коноид. Плоскость параллелизма занимает частное положение относительно плоскостей проекций. Она перпендикулярна H.
Анализ решения. Что нужно сделать для построения каркаса поверхности? Воспользовавшись тем, что плоскость параллелизма занимает частное положение а перпендикулярно H , мы можем построить горизонтальные проекции производящих  … параллельно горизонтальному следу плоскости а . После этого построить их фронтальные проекции не составит труда, так как нам известны горизонтальные проекции точек пересечения производящих с направляющими.
… параллельно горизонтальному следу плоскости а . После этого построить их фронтальные проекции не составит труда, так как нам известны горизонтальные проекции точек пересечения производящих с направляющими.
Для того чтобы определить горизонтальную проекцию точки A , следует воспользоваться условием принадлежности: точка принадлежит поверхности, если она находится на линии этой поверхности. В качестве такой линии удобно брать производящую, но в данном случае это невозможно, потому что мы не можем через A” провести фронтальную проекцию производящей. Проведем через фронтальную проекцию точки A фронтальную проекцию любой линии, горизонтальную проекцию которой можно построить по точкам ее пересечения с линиями каркаса. Теперь, используя линию связи, можно определить A’.
Алгоритм решения:
- Проводим ai параллельно
 до пересечения с горизонтальными проекциями направляющих.
до пересечения с горизонтальными проекциями направляющих. - Используя линии связи, найдем фронтальные проекции точек пересечения линий каркаса направляющими и проведем
 .
. - Проводим b”: A”
 b”. Отмечаем 1 ”, 2 ”, 3 ‘ и т. д.
b”. Отмечаем 1 ”, 2 ”, 3 ‘ и т. д. - Находим проекции точек 1 ‘, 2 ‘, 3 ‘, 4 ‘ и проводим b’.
- Находим A’
 b’.
b’.
Пример задачи 3
Построить проекции каркаса винтового транспортера. Дано: проекции вала транспортера (рис. 7) с осью i, перпендикулярной H , шаг винтовой линии h, наружный диаметр транспортера D . Производящая – прямая линия, параллельная плоскости H , в каждом положении пересекает винтовую линию и ось i. Найти горизонтальную проекцию A’ точки A, лежащей на поверхности транспортера по заданной фронтальной проекции A”.
Анализ данных. Определитель поверхности – геометрическая часть; производящая – прямая линия, направляющие – цилиндрическая винтовая линия l и прямая i , перпендикулярная H, плоскость параллелизма H . Поверхность транспортера – прямой (кольцевой) винтовой коноид.
Анализ решения. Построить проекции каркаса – изобразить ряд положений производящей поверхности. Так как производящая – горизонталь, то положение ее фронтальной проекции параллельно оси X. Так как один конец производящей перемещается по цилиндрической винтовой линии, а другой в любой момент времени пересекает ось, то можно утверждать, что на поверхности вала транспортера образуется цилиндрическая винтовая линия. Горизонтальную проекцию точки A найдем из условия принадлежности: если точка принадлежит поверхности, то она лежит на линии, принадлежащей поверхности. В качестве такой линии удобно взять производящую aA .
Алгоритм решения:
- Изображаем горизонтальную проекцию каркаса, взяв 12 производящих, равноотстоящих друг от друга.
- Строим фронтальную проекцию направляющей винтовой линии и винтовой линии на поверхности вала транспортера, разбив шаг винтовой линии на 12 промежутков.
- Строим фронтальную проекцию каркаса транспортера, зная, что линии каркаса – горизонтали.
- Находим горизонтальную проекцию точки A. Для этого проводим фронтальную проекцию производящей
 , на которой лежит точка A, строим ее горизонтальную проекцию
, на которой лежит точка A, строим ее горизонтальную проекцию  и искомую горизонтальную проекцию A’ точки A.
и искомую горизонтальную проекцию A’ точки A.

Рис. 7
Пример задачи 4
Построить фронтальную проекцию одного витка правой специальной трапецеидальной резьбы (профиль ABCD ) с шагом h на цилиндрическом стержне диаметром d .
Анализ данных. Можно утверждать, что точки C и D профиля описывают винтовые линии на цилиндре диаметра d, а точки A и B – на поверхности цилиндра диаметра D = d + 2A”B”. Так как направление винтовой линии правое, то подъем винтового выступа на видимой стороне цилиндра должен идти слева направо.
Алгоритм решения:
Решение задачи сводится к построению винтовых линий на цилиндрических поверхностях, что легко сделать, разделив окружности оснований цилиндров и шаг винта на одинаковое, равное количество частей. Отрезки BC , AD , AB, скользя по винтовым направляющим, образуют соответственно кольцевой косой геликоид, кольцевой прямой геликоид, цилиндрическую поверхность, ограничивающие виток. Следует помнить, что линия BC не будет линией очерка фронтальной проекции витка. Это будет некоторая кривая, очень близкая к прямой, касательной к проекциям винтовых линий, проходящих через точки B и C . На практике эту касательную и принимают за линию очерка.
Алгоритм решения (рис. 8).
- Делим окружность оснований цилиндров и шаг винта h(hAD; Нв; hС) на 12 равных частей.
- Строим винтовые линии, описываемые точками A, D, находя фронтальные проекции точек 1 – 14, аналогично строим винтовые линии, описываемые точками B и C .
- Строим очерк фронтальной проекции витка, проводя прямые a”, b”, касательные к винтовым линиям, описываемым точками B и C .
- Выделяем видимую и невидимую части витка.

Рис. 8
Возможно, вас также заинтересует эта ссылка:
Варианты задания № 2
Вариант 1. Построить проекции конуса вращения с вершиной в точке S и основанием радиусом R = 30 , расположенным на горизонтально-проецирующей плоскости  . Построить проекции точки A, принадлежащей конической поверхности.
. Построить проекции точки A, принадлежащей конической поверхности.
Вариант 2. Построить проекции конуса вращения с вершиной в точке S и основанием радиусом R = 30 , расположенным на фронтально-проецирующей плоскости  . Построить проекции точки A , принадлежащей конической поверхности.
. Построить проекции точки A , принадлежащей конической поверхности.
Вариант 3. Построить проекции конуса вращения с вершиной в точке S и основанием радиусом R = 30 , расположенным на плоскости, заданной двумя пересекающимися прямыми a и b. Построить проекции точки A, принадлежащей конической поверхности.
Вариант 4. Построить проекции конуса вращения с вершиной в точке S и основанием радиусом R = 30, расположенным на плоскости, заданной линией ската c . Построить проекции точки A, принадлежащей конической поверхности.
Вариант 5. Построить проекции цилиндрической поверхности вращения, заданной тремя прямыми a,b и  принадлежащими ее каркасу. Построить проекции образующей, проходящей через точку A.
принадлежащими ее каркасу. Построить проекции образующей, проходящей через точку A.
Вариант 6. Построить проекции цилиндрической поверхности вращения, заданной тремя прямыми a, b и  принадлежащими ее каркасу. Построить проекции образующей, проходящей через точку A.
принадлежащими ее каркасу. Построить проекции образующей, проходящей через точку A.
Вариант 7. Даны прямые a,b и  которые принадлежат каркасу конической поверхности. Построить проекции конуса, если известны истинные величины образующих (80 мм) и то, что направляющая – окружность. Найти проекции точки A, лежащей на поверхности.
которые принадлежат каркасу конической поверхности. Построить проекции конуса, если известны истинные величины образующих (80 мм) и то, что направляющая – окружность. Найти проекции точки A, лежащей на поверхности.
Вариант 8. Даны прямые a,b и  которые принадлежат каркасу конической поверхности. Построить проекции конуса, если известны истинные величины образующих (80 мм) и то, что направляющая – окружность. Найти проекции точки A, лежащей на поверхности.
которые принадлежат каркасу конической поверхности. Построить проекции конуса, если известны истинные величины образующих (80 мм) и то, что направляющая – окружность. Найти проекции точки A, лежащей на поверхности.
Вариант 9. Построить очерк поверхности вращения, заданной образующей m и осью i. Указать проекции экватора, горла и главного меридиана. Построить проекцию линии n, лежащей на поверхности цилиндроида.
Вариант 10. Построить очерк поверхности вращения, заданной образующей m и осью i. Указать проекции экватора, горла и главного меридиана. Построить проекцию линии n , лежащей на поверхности цилиндроида.
Варианты 11-20. Построить каркас воздухозаборника (крыши, оболочки, устоя опоры моста, поверхности дамбы), образованного перемещением прямолинейной производящей, по направляющим [AB] и n,  – плоскость параллелизма. Построить недостающие проекции точки C и линии b , лежащих на поверхности.
– плоскость параллелизма. Построить недостающие проекции точки C и линии b , лежащих на поверхности.
Варианты 21-24. Шнековый транспортер состоит из вала (диаметр d) и соединенного с ним винтового выступа. Построить проекции каркаса прямолинейных производящих поверхности шнека – косого геликоида. Дано: ось i, направляющий конус с углом при вершине  , горизонтальная проекция и шаг направляющей линии – правой цилиндрической винтовой линии. Построить недостающую проекцию точки A, лежащей на поверхности шнека.
, горизонтальная проекция и шаг направляющей линии – правой цилиндрической винтовой линии. Построить недостающую проекцию точки A, лежащей на поверхности шнека.






Возможно, вас также заинтересует эта ссылка:
Тема 3. Преобразование чертежа
Цель – закрепить знания о методах преобразования чертежа.
Решение многих задач способами начертательной геометрии в конечном счете сводится к определению позиционных и метрических характеристик геометрических фигур. В связи с этим задачи можно условно разделить на позиционные, решение которых дает ответ на вопрос о взаимном расположении геометрических фигур по отношению друг к другу и относительно плоскостей проекций, и метрические, решение которых позволяет определить расстояния и углы между элементами одной или нескольких фигур.
Трудоемкость графического решения задачи часто зависит не от ее сложности, а от того, какое положение по отношению к плоскостям проекций занимают геометрические фигуры, входящие в исходные данные, т.е. проекции могут быть «удобными» и «неудобными» для решения. Начертательная геометрия располагает большим количеством методов преобразования «неудобных» для решения ортогональных проекций в «удобные». Наибольшее распространение нашли методы, основу которых составляет изменение взаимного расположения плоскостей проекций и проецирующей фигуры за счет ее перевода в частное положение. Такое преобразование может быть осуществлено двумя путями:
1) переходом от заданной системы плоскостей проекций к новой, по отношению к которой данная геометрическая фигура, при этом не меняющая своего положения в пространстве, займет частное положение;
2) перемещением в пространстве заданной геометрической фигуры в частное положение. Плоскости проекций при этом остаются неизменными.
Для решения задачи следует вспомнить суть основных классических способов преобразования проекций.
1. Замена плоскостей проекций. Получение новых, более удобных проекций достигается за счет перехода от заданных плоскостей проекций к новым. Положение новых плоскостей проекций следует выбирать так, чтобы по отношению к ним проецируемая геометрическая фигура заняла частное положение. Переход от заданной системы  к новой может осуществляться по одной из следующих схем:
к новой может осуществляться по одной из следующих схем:
– замена одной плоскости  или
или  ;
;
– замена двух плоскостей  или
или  .
.
Замена одновременно только одной плоскости проекции обеспечивает неизменность одной плоскости, которая выполняет функции связующего звена между новой и исходной проекциями.
2. Метод плоскопараллельного перемещения. Перемещению подвергается геометрическая фигура, а плоскости проекций при этом остаются без изменения. Закон движения состоит в том, что все точки фигуры перемещаются по траекториям, расположенным в параллельных плоскостях. Траекториями движения могут служить и окружности, центры которых принадлежат одной прямой – оси вращения. Это частный случай метода плоскопараллельного перемещения, который называется способом вращения. В зависимости от расположения оси вращения различают способы вращения вокруг оси, перпендикулярной и параллельной плоскости проекций (вращение вокруг линии уровня).
Методы преобразования чертежа широко используются при решении прикладных задач. Почти во всех следующих заданиях потребуется использование преобразований. Здесь мы упомянем об их применении в машиностроении при построении на чертеже истинных величин сечений и поверхностей элементов деталей, при изображении на чертеже промежуточных положений элементов конструкций, определении отклонения осей деталей и узлов станка и т.п. При решении инженерных задач, связанных с векторами (теоретическая механика, теория механизмов и машин, сопротивление материалов), которые занимают общее положение относительно плоскостей проекций, также удобно пользоваться способами преобразования чертежа.

Рис. 9
Одной из важных областей применения начертательной геометрии является проектирование и вычерчивание режущего инструмента. Токарный резец (рис. 9) получается из призматического бруска. В результате заточки на одном конце бруска образуется головка, ограниченная несколькими различно расположенными поверхностями. Взаимное положение поверхностей, величина углов и положе-x ние кромок, образованных поверхностями, установлены для резцов различных типов на основе экспериментов. На рис. 9 видно, что плоскости, в результате сечения которыми образуется головка резца, занимают как частное, так и общее положение относительно плоскостей проекций. Следовательно, для Рис. 9 определения углов между гранями головки удобно воспользоваться способами преобразования чертежа. Эти углы необходимо знать для заточки резца на специальном станке.
Прежде чем рассмотреть несколько примеров, обратим внимание на то, когда целесообразно применять тот или иной способ преобразования. При использовании способа вращения следует иметь в виду, что вращение вокруг осей, перпендикулярных плоскостям проекций, в большинстве случаев приводит к запутанным построениям. Это часто происходит из-за наложения новых проекций на старые. Избежать наложения можно, применив способ параллельного перемещения. В этом случае одну из двух (две из четырех) проекций не строят, а перечерчивают на кальку, которую затем прикладывают в наиболее удобном месте чертежа. Следующую дополнительную проекцию строят с помощью проекции, изображенной на кальке, и одной из предшествующих.
Способ вращения вокруг главной линии следует рекомендовать для определения натуральной величины плоских фигур и решения метрических задач на плоскости.
Преимущества способа замены плоскостей проекций проявляется в уменьшении количества дополнительных проекций. Он дает наиболее рациональные решения в тех случаях, когда требуется выяснить взаимное расположение геометрических элементов.
Сочетание способа замены плоскостей проекций со способом вращения следует использовать в тех случаях, когда применение каждого из них в отдельности приводит к громоздким и неудобным построениям.
Пример задачи 5
Определить истинную величину лопасти ABCD по ее ортогональному чертежу. Изобразить на чертеже лопасть после поворота на 30° вокруг оси 1 – 2 (рис. 10, 11).
Анализ данных. Лопасть – трапеция, так как AB параллельна DC, которая занимает в пространстве общее положение.
Анализ решения. Какой метод преобразования чертежа использовать для решения задачи? Для решения первой ее части наиболее удобным будет способ вращения вокруг линии уровня. Решение в данном случае не будет слишком громоздким. Правда, вторую часть задачи этим способом не решить. Здесь следует использовать метод замены плоскостей проекций. Рассмотрим каждую часть задачи отдельно. Решая первую часть (см. рис. 10), мы должны вращением лопасти вокруг линии уровня (например, горизонтали h) привести ее в частное положение, при котором плоскость трапеции ABCD будет параллельна плоскости проекций (горизонтальной). В этом случае ее проекция на эту плоскость и даст истинную величину. Построить на чертеже проекции линии уровня лежащей в плоскости лопасти не сложно, так как мы знаем, что одна из проекций линии уровня параллельна оси координат, а другую найдем из условия принадлежности. Проекции радиусов вращения вершин трапеции ABCD относительно линии уровня строим, зная теорему о проецировании прямого угла и условия принадлежности. Очевидно, что в положении, при котором лопасть параллельна плоскости проекции, радиусы вращения будут проецироваться на эту плоскость в истинную величину, определяемую способом прямоугольного треугольника.

В какое частное положение нужно привести лопасть для решения второй задачи (рис. 10)? Нужно сделать так, чтобы ось вращения 1 – 2 стала проецирующей прямой, т.е. перпендикулярной к плоскости проекций. Тогда, очевидно, и плоскость лопасти будет проецирующей, и мы сможем легко отсчитать истинную величину угла поворота лопасти и изобразить новое положение ее проекций. Можно ли сделать прямую 1 – 2 проецирующей, произведя замену одной плоскости проекций? Нет, так как 1 – 2 – прямая общего положения, а при преобразовании чертежа необходимо сохранять ортогональность плоскостей проекции. Следовательно, потребуются две замены, в результате которых переведем прямую сначала в положение, параллельное плоскости проекции, а затем сделаем ее проецирующей.
Алгоритм решения:
Определение истинной величины лопасти (рис. 10)
- Проводим фронтальную проекцию горизонтальной плоскости ABCD : h”(A”,3″ ).
- Используя A’ и 3′, строим h’.
- Находим проекции центра вращения точки B, для чего проводим через точку B’ перпендикуляр h’. Отмечаем точку пересечения 4′, находим 4″. Точка 4 – искомый центр вращения.
- Определим величину радиуса вращения B — 4 как гипотенузу прямоугольного треугольника B’ 4′ 5′, у которого катет 4′ 5′ = /zB — z4/ =
 .
. - Из центра 4′ проводим дугу радиусом B’5′, точка пересечения которой с прямой B’4 ‘ укажет положение точки
 , когда ABCD параллельно H.
, когда ABCD параллельно H. - Найдем положение точки
 как пересечение перпендикуляра из точки C’ к h’ и прямой B’ – 3 ‘, и точки
как пересечение перпендикуляра из точки C’ к h’ и прямой B’ – 3 ‘, и точки  как пересечение прямой, проходящей через D’ перпендикулярно h’, и прямой через точку C параллельно AB.
как пересечение прямой, проходящей через D’ перпендикулярно h’, и прямой через точку C параллельно AB. - Соединяем точки
 .
.
Построение проекций лопасти после поворота на 30° (см. рис. 11)
1. Переходим от системы  к
к  . Меняем плоскость
. Меняем плоскость  на
на  так, чтобы [1-2] была параллельна
так, чтобы [1-2] была параллельна  . При этом X1 параллельна 1′ – 2′.
. При этом X1 параллельна 1′ – 2′.
2. Строим новую фронтальную проекцию лопасти  , основываясь на том, что координаты точек по оси Z остаются неизменными.
, основываясь на том, что координаты точек по оси Z остаются неизменными.
3. Переходим от системы  к
к  . Меняем плоскость
. Меняем плоскость  на
на  так, чтобы [1-2] было перпендикулярно
так, чтобы [1-2] было перпендикулярно  . При этом X2 перпендикулярно
. При этом X2 перпендикулярно  .
.
4. Строим новую горизонтальную проекцию лопасти, помня о том, что координаты у точек остаются неизменными.
5. Поворачиваем новую горизонтальную проекцию лопасти вокруг оси 1 – 2 на 30° по часовой стрелке в положение  .
.
6. Найдем положение точек  , зная, что траектория их перемещения на
, зная, что траектория их перемещения на  – прямая, параллельная X2.
– прямая, параллельная X2.
7. Построим проекции лопасти в системе  после поворота, помня о неизменности координаты Y при переходе от системы
после поворота, помня о неизменности координаты Y при переходе от системы  к
к  и координаты Z от
и координаты Z от  к
к  .
.
Пример задачи 6
Определить величину угла между гранями ABC и BCD рабочей части фрезы (рис. 12).
Анализ данных. Положение граней рабочей части фрезы задано однозначно. Анализ решения. Каким образом на чертеже получить истинную величину искомого угла? Двугранный угол будет проецироваться на плоскость в истинную величину, если плоскость будет перпендикулярна ребру двугранного угла. Ребро – прямая общего положения. Привести ее в проецирующее положение удобно заменой плоскостей проекций.

Рис. 12
Алгоритм решения:
- Переходим от системы
 к
к  . Меняем плоскость
. Меняем плоскость  на
на  так, чтобы BC была параллельна
так, чтобы BC была параллельна  . При этом X1 // B’C’.
. При этом X1 // B’C’. - Строим новые фронтальные проекции ребер BD, AB и BC.
- Переходим от системы
 к
к  . Меняем плоскость
. Меняем плоскость  на
на  так, чтобы BC была перпендикулярна
так, чтобы BC была перпендикулярна  . При этом X2
. При этом X2  .
. - Строим новые горизонтальные проекции ребер BD, AB и BC . Угол
 – искомый. Функционирование космического аппарата (рис. 13) обеспечивается электроэнергией получаемой путем преобразования солнечного излучения. Для преобразования солнечной энергии на панели солнечной батареи располагаются полупроводниковые фотоэлектрические преобразователи (ФЭП). Для наиболее эффективной работы ФЭП необходима ориентация батареи на Солнце таким образом, чтобы солнечные лучи падали на панель батареи под углом близким к 90°.
– искомый. Функционирование космического аппарата (рис. 13) обеспечивается электроэнергией получаемой путем преобразования солнечного излучения. Для преобразования солнечной энергии на панели солнечной батареи располагаются полупроводниковые фотоэлектрические преобразователи (ФЭП). Для наиболее эффективной работы ФЭП необходима ориентация батареи на Солнце таким образом, чтобы солнечные лучи падали на панель батареи под углом близким к 90°.
На рис. 14 приведена конструкция солнечной батареи: 1 – панели; 2 – металлический каркас; 3 – капроновая сетка; 4 – пластины ФЭП.

Формы панелей солнечных батарей могут быть различными. Наиболее часто используются формы (рис. 15).

Рис. 15
Возможно, вас также заинтересует эта ссылка:
Варианты задания № 3
Варианты 1-12. Дано: ортогональный чертеж панели солнечной батареи. Направление падения солнечных лучей. Определить истинную величину панели и угол между ее плоскостью и направлением солнечных лучей.
Варианты 13-18. Солнечная батарея состоит из двух панелей, направление солнечных лучей l. После поворота вокруг оси 1-2 панель 1-3-4-2 переводится в ту же плоскость, в которой лежит панель 1-2-6-5. Определить необходимый угол поворота и угол между солнечными лучами и полученной плоскостью.
Варианты 19-24. Дано: ортогональный чертеж панели солнечной батареи. Определить двумя способами истинную величину панели и углы наклона панели к плоскостям проекций.








Возможно, вас также заинтересует эта ссылка:
Тема 4. Сечение поверхности плоскостью
Цель – выработать навыки построения линий сечения поверхностей плоскостями частного положения, определить величину и форму сечения.
Для решения задания необходимо вспомнить общий алгоритм решения задачи о пересечении поверхностей ( и
и  ).
).
1. Вводим вспомогательную поверхность  .
.
2. Определяем линии пересечения поверхности  с поверхностями
с поверхностями  и
и  : (mi) =
: (mi) =  ; (ni) =
; (ni) =  .
.
3. Определяем точку (точки пересечения) линий пересечения mi и ni: Li = mi  ni.
ni.
4. Повторяем записанные операции n раз и определяем n точек L. Соединив их плавной кривой получаем искомую кривую l:
(l) = L1  L2
L2  L3…Ln.
L3…Ln.
Если одна из фигур – плоскость, а вторая – линейчатая поверхность, то решение сводится к нахождению точек пересечения образующих поверхности с секущей плоскостью, т.е. к нахождению точки пересечения прямой с плоскостью. При построении сечения многогранника задача может быть так же сведена к многократному решению задачи по определению пересечения двух плоскостей – грани многогранника и секущей плоскости. Задача существенно упрощается, если секущая плоскость проецирующая. В этом случае задача сводится к построению второй проекции сечения; одна его проекция, лежащая в секущей плоскости, уже есть. Для этого следует воспользоваться условиями принадлежности. Истинная величина и форма сечения находятся методами преобразования чертежа.
Линии пересечения плоскостей с поверхностями, наклонные сечения часто встречаются в реальных конструкциях. Часто на чертежах различных деталей (отливок, поковок) требуется строить проекции кривых линий, по которым плоскости пересекаются с различными телами вращения. Такие линии называются линиями среза (рис. 16). Каждую деталь можно рассматривать как комбинацию простых геометрических элементов, поэтому полезно напомнить форму сечения простых поверхностей вращения плоскостью (табл. 1).
Таблица 1.1



При вычерчивании проекций реальных деталей приходится выполнять всевозможные сопряжения. При построении линии среза часто необходимо вычертить сопряжение дуги окружности и прямой с помощью заданного радиуса. Сначала определяют множество возможных положений центров дуг сопряжения заданного радиуса R1 (рис. 16,а), для чего на расстоянии R1 от прямой a проводят параллельную ей прямую m.

Рис. 16
Из центра O радиусом R + R1 проводят концентрические окружности. Точка O1 будет центром дуги сопряжения. Точка сопряжения C получена на перпендикуляре, проведенном из точки O к прямой a , а точка B – на прямой, соединяющей точки O и O1. Сопряжение дуг двух окружностей при помощи прямой линии сводится к построению внешней или внутренней касательной к этим окружностям. Для проведения внешней касательной, сопрягающей две окружности радиусами R и R1 (рис. 16,б), сначала соединяют центры окружностей, затем отрезок делят точкой O2 пополам, а из точки O проводят окружность радиусом, равным разности радиусов заданных окружностей R – R1. На этой окружности радиусом О2 O засекают точки E и D. Продлив отрезки OE и OD до пересечения с окружностью радиусом R, получают точки сопряжения C и B. Соединяют точки E и D с центром O1. Из точки C и B параллельно прямым O1E и O1D проводят прямые, сопрягающие две окружности. Такие сопряжения на окружности радиусом R1 можно получить, проведя из точки O1 прямые, перпендикулярные прямым O1E и O1D . Построение касательных, сопрягающих окружности R и R1, аналогично предыдущему (16,в).
Пример задачи 7
Деталь образуется снятием материала заготовки по плоскости а (рис. 17). Построить горизонтальную проекцию детали, найти истинную величину сечения.
 Рис. 17
Рис. 17
Анализ данных. Деталь представляет собой сочетание пяти цилиндрических (три из них -отверстия) и одной конической поверхности, оси которых перпендикулярны горизонтальной плоскости проекции. Плоскость  фронтально-проецирующая.
фронтально-проецирующая.
Анализ решения. Первая часть задачи сводится к построению линий пересечения фронтально-проецирующей плоскостью  поверхностей, на которые можно расчленить деталь. Как явствует из приведенной выше табл. 1, линии сечения всех рассматриваемых поверхностей – эллипсы. Так как цилиндрические поверхности являются проецирующими на плоскость H, то на горизонтальной проекции линии их сечения совпадут с проекциями поверхностей. Горизонтальную проекцию линии сечения конической части удобно построить с помощью вспомогательных секущих плоскостей, параллельных H.
поверхностей, на которые можно расчленить деталь. Как явствует из приведенной выше табл. 1, линии сечения всех рассматриваемых поверхностей – эллипсы. Так как цилиндрические поверхности являются проецирующими на плоскость H, то на горизонтальной проекции линии их сечения совпадут с проекциями поверхностей. Горизонтальную проекцию линии сечения конической части удобно построить с помощью вспомогательных секущих плоскостей, параллельных H.
Для решения второй части задачи следует воспользоваться одним из способов преобразования чертежа – сделать так, чтобы сечение спроецировалось на одну из плоскостей проекций в натуральную величину.
Алгоритм решения:
- Строим горизонтальную проекцию линии сечения конической части детали с помощью вспомогательных плоскостей Ti //
 . Линия пересечения плоскости
. Линия пересечения плоскости  с верхним основанием усеченного конуса – прямая 1-2.
с верхним основанием усеченного конуса – прямая 1-2. - Линия пересечения верхнего основания цилиндра I с плоскостью
 – прямая 12-14.
– прямая 12-14. - Линии пересечения верхнего основания цилиндра II с
 прямые – [19-20], [21-22].
прямые – [19-20], [21-22]. - Переходим от системы
 к
к  . При этом X1 //
. При этом X1 //  . Строим новую горизонтальную проекцию сечений детали плоскостью а , помня, что координаты y для
. Строим новую горизонтальную проекцию сечений детали плоскостью а , помня, что координаты y для  и
и  неизменны. Отсчет координат удобно вести от осей симметрии (см. точки 22′ и
неизменны. Отсчет координат удобно вести от осей симметрии (см. точки 22′ и  ).
).
Пример задачи 8
Построить линию среза детали, образованной из заготовки (тело вращения), срезанной плоскостями  , параллельными фронтальной плоскости проекций (рис. 18).
, параллельными фронтальной плоскости проекций (рис. 18).

Рис. 18
Анализ данных. Как видно из чертежа, заготовка образована из сферы и двух цилиндров, которые сопрягаются между собой с помощью поверхностей вращения – торов. Правый цилиндр завершается полусферой. Установить участки поверхностей вращения, ограничивающих рассматриваемую деталь, можно при помощи точек сопряжения, найденных на линиях центров или на перпендикулярах к образующим.
Анализ решения. Решение задачи сводится к построению сечения плоскостью частного положения тел вращения, образующих заготовку. Из чертежа видно, что цилиндр I плоскостями не рассекается. Согласно табл. 1 в сечении цилиндра II получим две прямые линии, в сечении сферы и полусферы – окружности, а в сечении торовых поверхностей – кривые более высокого порядка, которые можно построить, используя вспомогательные плоскости, параллельные  . Решение следует начать с нахождения характерных точек линии среза, которые определяются с помощью вспомогательных секущих плоскостей аi //
. Решение следует начать с нахождения характерных точек линии среза, которые определяются с помощью вспомогательных секущих плоскостей аi //  , проведенных через точки сопряжений.
, проведенных через точки сопряжений.
Алгоритм решения:
- Находим точки сопряжения A, B, C на очерковых образующих детали и проводим через них плоскости
 и
и  , параллельные
, параллельные  . Плоскость
. Плоскость  рассекает поверхность по окружности радиусом r1. На плоскость
рассекает поверхность по окружности радиусом r1. На плоскость  эта окружность проецируется в истинную величину.
эта окружность проецируется в истинную величину. - Определяем профильную проекцию I “‘ точки I – пересечения окружности радиуса r1 и профильного следа
 секущей плоскости
секущей плоскости  .
. - Определяем фронтальную проекцию I” точки I.
- Аналогично находим проекции точки 3.
- Строим линию среза на сфере – окружности радиуса rc от точки I” до точки 2″ пересечения окружности радиуса rc с фронтальным следом
 .
. - Определим положение крайней левой точки линии среза – точки 4. Для этого проводим плоскость а3 //
 так, чтобы она рассекала поверхность детали по окружности радиусом r3, которая касается плоскости среза
так, чтобы она рассекала поверхность детали по окружности радиусом r3, которая касается плоскости среза  .
. - Для построения линии среза тора I проведем плоскость а4 //
 и найдем точку 5.
и найдем точку 5. - Для построения среза тора II проведем плоскость а5 //
 и найдем точку 6. Для более точного построения линии среза следует взять несколько промежуточных вспомогательных секущих плоскостей.
и найдем точку 6. Для более точного построения линии среза следует взять несколько промежуточных вспомогательных секущих плоскостей. - Строим линию среза на цилиндре II. Для этого проводим прямую из точки 3″, параллельно оси детали до пересечения с
 в точке 7″.
в точке 7″. - Точка 7″ определяет величину радиуса окружности линии среза на полусфере.
- Достраиваем линию среза до полной пользуясь тем, что она симметрична оси детали.
Возможно, вас также заинтересует эта ссылка:
Варианты задания № 4
Варианты 1-12. Построить чертеж детали, получаемой обработкой изображенной на чертеже заготовки, так, чтобы проецирующими плоскостями отсекалась ее часть; следы указаны на чертеже. Показать истинную величину сечения заготовки плоскостью  . Линии невидимого контура можно на чертеже не изображать.
. Линии невидимого контура можно на чертеже не изображать.
Варианты 13-24. Закончить изображение фронтальной проекции детали (построить фронтальную проекцию линии среза), получаемой заготовки (тело вращения) путем срезания по плоскостям  и
и  параллельно оси вращения. Указать границы перехода одной поверхности в другую. Все построения по определению центров радиусов сопряжения, точек сопряжения и прочие на чертеже должны быть сохранены (рис. 18).
параллельно оси вращения. Указать границы перехода одной поверхности в другую. Все построения по определению центров радиусов сопряжения, точек сопряжения и прочие на чертеже должны быть сохранены (рис. 18).






Тема 5. Пересечение поверхностей
Цель – применить знания о построении в ортогональных проекциях линий пересечения поверхностей.
Линия пересечения кривых поверхностей может быть плоской и пространственной. Возможны четыре случая взаимного пересечения:
1. Частичное врезание, когда часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения – замкнутая пространственная кривая (рис. 19).
2. Полное проникание: все образующие одной поверхности пересекаются со второй поверхностью. Линии пересечения распадаются на две (или больше) отдельные кривые (рис. 20).

Рис. 19 Рис. 20
3. Одностороннее внутреннее соприкосновение: пересекающиеся поверхности имеют в одной точке общую плоскость касания (рис. 21). Эта точка на кривой пересечения является или угловой (точка излома), или узловой (двойной).
4. Двойное соприкосновение: пересекающиеся поверхности имеют в двух точках общие касательные плоскости. В этом случае в пересечении участвуют все образующие обеих поверхностей и они пересекаются по двум кривым линиям (рис. 22).
 Рис. 21 Рис. 22
Рис. 21 Рис. 22
Следует иметь в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей (рис. 23).

Рис. 23
Вспомогательные плоскости применяются в тех случаях, когда они пересекают заданные поверхности по прямым или окружностям или по таким линиям, которые проецируются на основную или какую-нибудь дополнительную плоскость проекций в виде прямых линий или окружностей. Вспомогательные плоскости могут представлять собой семейство параллельных плоскостей или пучок плоскостей. Чаще всего используют проецирующие вспомогательные плоскости (перпендикулярные плоскостям проекций). Это существенно облегчает решение задачи благодаря тому, что на чертеже сразу определяется одна из проекций линии пересечения посредника с поверхностью.
С помощью семейства параллельных плоскостей решают следующие задачи:
1) пересечение двух поверхностей вращения с параллельно расположенными осями. Очевидно, что секущие плоскости перпендикулярны осям вращения;
2) пересечение сферы с произвольно расположенной поверхностью второго порядка, имеющей семейство окружностей, В этом случае посредники должны проходить через эти окружности (круговое сечение);
3) пересечение двух цилиндров (вращения или эллиптических) с пересекающимися или скрещивающимися осями, когда вспомогательные плоскости параллельны осям обоих цилиндров. В сечении получаются образующие;
4) пересечение тора и цилиндра, если последний лежит в плоскости, перпендикулярной оси вращения тора.
Рассмотрим пример (рис. 24). Для построения линии пересечения сферы с конусом в качестве посредников выберем плоскости, параллельные плоскости п , – горизонтальные плоскости. В этом случае обе поверхности будут рассекаться по окружностям, построить проекции которых и найти их точки пересечения весьма просто.
 Рис. 24
Рис. 24
Если в качестве посредников брать фронтальные или профильные плоскости, то на конусе придется строить гиперболы, что достаточно трудоемко и приводит к потере точности. Экстремальными будут точки A и B, фронтальные проекции которых принадлежат очеркам поверхностей. При рассечении поверхностей плоскостью  находим точки M и N . Точность построения линии пересечения определяется количеством посредников.
находим точки M и N . Точность построения линии пересечения определяется количеством посредников.
Использовать семейство параллельных плоскостей можно и в том случае, когда вспомогательная плоскость пересекает одну из поверхностей вращения по эллипсам. Для этого следует преобразовать чертеж так, чтобы эллипсы, получающиеся в сечении, проецировались на вспомогательную плоскость в окружности. Рассмотрим построение линии пересечения эллиптического конуса и кругового цилиндра (рис. 25). В качестве посредников выберем плоскости, параллельные основанию конуса. Они будут рассекать цилиндр по образующим, а конус – по подобным эллипсам. Произведем замену плоскостей так, чтобы эллипсы проецировались на новую плоскость в окружности. Как выставить новую горизонтальную плоскость проекций? Для определения потребного направления проецирования используем эллипс верхнего основания конуса. Из фронтальной проекции центра проведем окружность радиусом, равным малой полуоси. Касательная к этой окружности, проведенная из фронтальной проекции точки L, и даст искомое направление, а значит, и расположение новой горизонтальной плоскости проекций. Проведем секущую плоскость  . Проекцией сечения конуса на плоскость
. Проекцией сечения конуса на плоскость  будет окружность. Цилиндр рассечется по образующим, которые в системе
будет окружность. Цилиндр рассечется по образующим, которые в системе  будут фронталями. Точки пересечения горизонтальных проекций этих фронталей с окружностью и определят точки, принадлежащие линии пересечения заданных поверхностей. Описанная операция повторяется столько раз, сколько необходимо для обеспечения потребной точности построения линии пересечения.
будут фронталями. Точки пересечения горизонтальных проекций этих фронталей с окружностью и определят точки, принадлежащие линии пересечения заданных поверхностей. Описанная операция повторяется столько раз, сколько необходимо для обеспечения потребной точности построения линии пересечения.
 Рис. 25
Рис. 25
С помощью пучка плоскостей (вращающейся плоскости) можно решить следующие задачи:
1) построение линии пересечения двух произвольно расположенных конусов второго порядка. Осью пучка является прямая, проходящая через вершины конусов;
2) пересечение конуса и цилиндра. Осью пучка является прямая, проходящая через вершину конуса параллельно оси цилиндра.
Рассмотрим пример на построение линии пересечения двух конических поверхностей (рис. 26).
Ось вращения вспомогательных плоскостей определим как линию a, соединяющую вершины конусов. Найдем горизонтальный след этой прямой Ha. Любая вспомогательная плоскость теперь будет определяться двумя пересекающимися прямыми: осью вращения и горизонтальным следом – прямой, лежащей в плоскости  и проходящей через точку Ha. Секущая плоскость
и проходящей через точку Ha. Секущая плоскость  рассечет конус с вершиной S2 по образующим (так как проходит через вершину конусов) S23 и S22 и будет касательной по отношению к конусу с вершиной S1. Линии касания – S1. Точки пересечения указанных образующих и дадут точки, принадлежащие линии пересечения конусов.
рассечет конус с вершиной S2 по образующим (так как проходит через вершину конусов) S23 и S22 и будет касательной по отношению к конусу с вершиной S1. Линии касания – S1. Точки пересечения указанных образующих и дадут точки, принадлежащие линии пересечения конусов.
 Рис. 26
Рис. 26
Описанная операция повторяется многократно. Диапазон использования посредников определяется плоскостями касания к одной и другой поверхностям –  и
и  . Точки видимости -точки пересечения очерковых образующих одного конуса с поверхностью другого.
. Точки видимости -точки пересечения очерковых образующих одного конуса с поверхностью другого.
Вспомогательные сферы могут быть использованы в случае, если обе поверхности являются поверхностями вращения и их оси пересекаются – поверхности имеют общую плоскость симметрии. Сфера пересекается с соосной поверхностью вращения по окружности, плоскость которой является проецирующей и на одной из плоскостей проекций отражается в прямую (рис. 27), что позволяет легко находить общие точки двух поверхностей вращения. При указанных выше условиях применяют концентрические сферы с центром в точке пересечения осей заданных поверхностей. Диапазон изменения радиуса посредника выбирается из следующих соображений. Наибольший радиус сферы Rmax равен расстоянию до наиболее удаленной точки пересечения очерков заданных поверхностей. Радиус наименьшей вспомогательной сферы равен радиусу большей из двух сфер, которые можно вписать в пересекающиеся поверхности.
 Рис. 27
Рис. 27
Рассмотрим пример (рис. 28). Впишем сферу в вертикально стоящую поверхность вращения. Линия касания – окружность, параллельная плоскости  . Ее фронтальная – прямая линия. Эта сфера Rmin рассечет наклонный цилиндр по окружности, фронтальная проекция которой тоже прямая линия. Общая точка – C . Сфера максимального радиуса Rmax = O”A”. Нахождение промежуточных точек с использованием сфер Rmin
. Ее фронтальная – прямая линия. Эта сфера Rmin рассечет наклонный цилиндр по окружности, фронтальная проекция которой тоже прямая линия. Общая точка – C . Сфера максимального радиуса Rmax = O”A”. Нахождение промежуточных точек с использованием сфер Rmin  R
R  Rmax ясно из чертежа. Точки A и B являются точками видимости на
Rmax ясно из чертежа. Точки A и B являются точками видимости на  . На фронтальной плоскости проекций видимая и невидимая части линии пересечения сливаются. Видимость на горизонтальной плоскости проекций определяется точками пересечения очерковых образующих цилиндра с поверхностью вращения (E).
. На фронтальной плоскости проекций видимая и невидимая части линии пересечения сливаются. Видимость на горизонтальной плоскости проекций определяется точками пересечения очерковых образующих цилиндра с поверхностью вращения (E).
 Рис. 28
Рис. 28
Если одна из поверхностей является поверхностью вращения, а вторая имеет семейство говых сечений, причем обе поверхности имеют общую плоскость симметрии, на которую круговые сечения второй поверхности проецируются в виде прямых линий, то для построения линии пересечения используются эксцентричные сферы. Принцип определения центра вспомогательной сферы можно проследить на рис. 29. Центрами вспомогательных сфер будут точки пересечения оси вращения первой поверхности с перпендикулярами, восстановленными в центре произвольно выбранного кругового сечения второй поверхности. Радиус сферы равен радиусу окружности, проходящей через концы отрезка, – проекции кругового сечения.

Рис. 29
С помощью эксцентрических сфер можно решать следующие задачи на пересечение поверхностей:
1) поверхности вращения и кругового тора, если ось первой лежит в плоскости симметрии тора, перпендикулярной его оси вращения;
2) сферы с поверхностью второго порядка, имеющей круговые сечения, если плоскость симметрии этой поверхности, на которую круговые сечения проецируются в виде прямых линий, является меридиональной плоскостью сферы;
3) поверхности вращения и эллиптического цилиндра или конуса, если заданные поверхности имеют общую плоскость симметрии и круговые сечения эллиптического цилиндра или конуса на эту плоскость проецируются в виде прямых линий.
Пример решения приведен на рис. 30.
 Рис. 30
Рис. 30
Строим линию пересечения конуса с тором. Выберем на торовой поверхности окружность. Для этого проведем через ось тора фронтально-проецирующую плоскость  . Выбранная окружность на фронтальной плоскости проекций будет представлена отрезком A”B”. Найдем центр и радиус вспомогательной сферы, которая будет рассекать тор по этой окружности так, чтобы центр лежал на оси конуса. Проведем через середину отрезка A” B” перпендикуляр до пересечения с осью конуса. Сфера, проведенная через точку O, рассечет торовую поверхность по выбранной нами окружности, конус – по окружности, параллельной плоскости
. Выбранная окружность на фронтальной плоскости проекций будет представлена отрезком A”B”. Найдем центр и радиус вспомогательной сферы, которая будет рассекать тор по этой окружности так, чтобы центр лежал на оси конуса. Проведем через середину отрезка A” B” перпендикуляр до пересечения с осью конуса. Сфера, проведенная через точку O, рассечет торовую поверхность по выбранной нами окружности, конус – по окружности, параллельной плоскости  (фронтальная проекция C” D”). Общая для них точка M принадлежит искомой линии пересечения. Указанная операция повторяется исходя из требований к точности построений.
(фронтальная проекция C” D”). Общая для них точка M принадлежит искомой линии пересечения. Указанная операция повторяется исходя из требований к точности построений.
Вспомогательные секущие сферы могут использоваться для построения линий перехода в корпусах промышленных изделий, получаемых литьем. Это нужно не только для построения проекционных моделей, но и для изготовления форм и моделей для процесса отливки. На рис. 31 показано использование способа концентрических сфер на чертеже вентиля для построения фронтальной проекции линии пересечения цилиндра Ф с тором  . Центром вспомогательных сфер будет точка пересечения осей. Радиус вспомогательных сфер лежит в диапазоне O”M ”
. Центром вспомогательных сфер будет точка пересечения осей. Радиус вспомогательных сфер лежит в диапазоне O”M ”  Rb < O”N”.
Rb < O”N”.
Сфера радиусом O”P” рассечет цилиндр и тор по окружностям, фронтальные проекции которых – отрезки L”K” и M”P”. Общая точка T” – вершина искомой кривой. Еще две точки найдем с помощью сферы радиусом Rb1 .
На рис. 32 показано построение проекций линии перехода корпуса для наружной и внутренней поверхностей способом эксцентрических сфер.

Рис. 31
 Рис. 32
Рис. 32
В случае, когда одна из пересекающихся поверхностей является проецирующей, отпадает необходимость использования посредников, так как можно использовать условие принадлежности. На рис. 33 показано построение линии пересечения сферы с цилиндром. Особенностями данной задачи является проецирующее положение цилиндрической поверхности и одностороннее внутреннее соприкосновение поверхностей. Узловая точка линии пересечения – точка соприкосновения 1 – лежит в плоскости симметрии на главном меридиане сферы. Фронтальная проекция цилиндра совпадает с фронтальной проекцией искомой линии пересечения.
Следовательно, задачу можно сформулировать так: задана фронтальная проекция линии пересечения двух тел. Найти ее горизонтальную и профильную проекции. Принцип решения покажем на примере точки K. Так как эта точка принадлежит обеим поверхностям, то она лежит и на поверхности сферы. Радиус параллели, на которой она лежит, равен расстоянию от оси до T”. Проводим горизонтальную проекцию этой окружности и находим на ней K’. Дальше действуем аналогично. Точки 2,8,4,10 являются точками видимости на соответствующих плоскостях проекции.

Рис. 33
На рис. 34 представлена задача на пересечение тора с цилиндром, когда также имеет место случай одностороннего внутреннего соприкосновения, но точка соприкосновения, в отличие от рассмотренного ранее примера, является угловой или точкой излома. Так как цилиндр горизонтально-проецирующий, то решение сводится к нахождению фронтальных и профильных проекций точек, лежащих на торовой поверхности (на параллелях тора). Суть построения ясна из рисунка. Угловая точка лежит на экваторе торовой поверхности.

Рис. 34
Линия пересечения поверхностей второго порядка есть алгебраическая кривая четвертого порядка. На практике используют ситуации, в которых кривая четвертого порядка распадается на более простые кривые низших порядков (например, на четыре прямые при пересечении двух цилиндров – рис. 35).
Весьма важным является случай распадания кривой четвертого порядка на две плоские кривые второго порядка. Признаки такого распадания сформулированы в следующих теоремах.
1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и еще по одной кривой, которая тоже будет плоской (рис. 36).
2. Если две поверхности второго порядка имеют две точки соприкосновения, то линия их пересечения распадается на пару кривых второго, плоскости которых проходят через прямую, соединяющую точки соприкосновения (рис. 36). Эта теорема называется теоремой о двойном соприкосновении.
 Рис. 35 Рис. 36
Рис. 35 Рис. 36
Пример решения задачи с использованием теоремы о двойном соприкосновении приведен на рис. 37. Нужно построить линию пересечения полуцилиндра с конусом. Точки соприкосновения – 3. Знание теоремы позволяет при решении задачи не использовать посредников. Строим фронтальную проекцию линии пересечения – два эллипса, проходящих через точки соприкосновения и точки пересечения образующих цилиндра и конуса. Горизонтальную проекцию строим из условия принадлежности. Точка 2 лежит на поверхности цилиндра. Значит, она лежит на образующей (прямой линии), находящейся на расстоянии Y2 от плоскости симметрии. На горизонтальной проекции этой образующей лежит горизонтальная проекция точки 2.

Рис. 37
3. Если две поверхности второго порядка имеют общую плоскость симметрии, то линия их пересечения проецируется на эту плоскость в виде кривой второго порядка.
4. Теорема Монжа. Если две поверхности второго порядка описаны около третьей или вписаны в нее, то они пересекаются по двум плоским кривым, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания. На рис. 38, 39 представлены примеры построения линии пересечения поверхностей I и II, описанных около или вписанных в поверхность III.
 Рис. 38 Рис. 39
Рис. 38 Рис. 39
Доказательство теоремы Монжа основано на использовании теоремы о двойном соприкосновении. Обратимся к рис. 38, где показаны две конические поверхности. Очевидно, что поверхности I и III, так же как и поверхности II и III, соприкасаются по плоским кривым, лежащим на поверхности III. Эти линии пересекаются в двух точках. Касательные плоскости, построенные в этих точках, будут касательными к обеим поверхностям. Таким образом, обе поверхности имеют двойное соприкосновение в данных точках и на основании теоремы о двойном соприкосновении пересекаются по плоским кривым, проходящим через прямую, соединяющую точки соприкосновения.
На рис. 40 приведены часто встречающиеся на практике варианты пересечения цилиндров и конусов вращения, описанных около сферы.

Рис. 40
Примером практического применения теоремы Монжа может служить конструирование трубопроводов из листового материала, моделей для отливки фитингов, построение линий пересечения отверстий одинакового диаметра (рис. 41) и т.д.
Пусть требуется соединить коническую емкость a с цилиндрическим трубопроводом b под прямым углом (рис. 42). Причем расстояние от трубы до днища емкости можно менять в довольно широком диапазоне. В этом случае можно построить линию пересечения поверхностей для фиксированного расстояния, нанести ее на обе поверхности, осуществить обработку по этим линиям и произвести сварку.
Технологический процесс обработки в таком варианте будет сложным и трудоемким. Проще было бы резать обе поверхности по проецирующим плоскостям. При использовании теоремы Монжа это возможно. Подберем точку пересечения осей конуса и цилиндра (O ) так, чтобы она являлась центром сферы, около которой описаны заданные геометрические тела. Окружность касания конуса и сферы на фронтальной плоскости спроецируется как отрезок А”В”, а окружность касания цилиндра и сферы – как C”D”. Точка пересечения линий касания – 1″. Соединяем точки E” и F” с точкой 1″ и получаем фронтальную проекцию искомой линии пересечения.

Задачи на построение линий пересечения поверхностей условно можно разбить на три группы:
1) технологические – построение линий пересечения элементов деталей, образующихся в процессе изготовления и обработке;
2) конструкторские – построение линий пересечения элементов конструкций, например в производстве летательных аппаратов (крыла и мотогондолы, корпуса и сопла), в строительстве и архитектуре (элементов кровли, всевозможных оболочек);
3) задачи, которые возникают при проведении научных исследований, например в области газовой динамики.
Рассмотрим задачу о построении линий пересечения газовых струй, линий пересечения поверхности струи с конструкцией, в области радиолокации и т.п.
Пример задачи 9
Построить горизонтальную проекцию выемки, которая образуется на неподвижной цилиндрической детали при обработке вращающейся конической фрезой, перемещающейся в направлении от точки O1 до точки O2 (рис. 43).
Анализ данных. Поверхность детали фронтально-проецирующая, фреза перемещается параллельно горизонтальной плоскости проекций.
Анализ решения. При обработке вращающейся фрезой, перемещающейся параллельно плоскости проекции, на детали образуется линия, соответствующая линии сечения детали плоскостью, угол наклона которой к плоскостям проекций определяется через угол конусности фрезы. Следовательно, задача распадается на две части: нахождение линии сечения плоскостью на участке движения фрезы и нахождение линии пересечения цилиндра с конусом в конечном положении фрезы. Обе части решаются введением вспомогательных секущих поверхностей, в качестве которых удобно выбрать плоскости, параллельные горизонтальной плоскости проекций. При их введении на поверхности цилиндра легко найти образующие, по которым он рассекается этими плоскостями, а на поверхности фрезы – окружности и их траектории при поступательном движении. Линии, принадлежащие одной секущей плоскости, пересекаются, образуя точки контура искомой выемки.
Алгоритм решения:
- Вводим вспомогательные секущие плоскости
 , которые рассекают конус по окружности mi, а цилиндр по образующим Ki .
, которые рассекают конус по окружности mi, а цилиндр по образующим Ki . - Находим
 .
. - Проводим траектории движения окружности mi.
- Находим точки пересечения траекторий с соответствующими образующими цилиндра. Соединяем горизонтальные проекции этих точек до момента прекращения поступательного движения фрезы.
- Определяя точки пересечения образующих с окружностями при нахождении фрезы в точке O2, достраиваем проекции выемки.
 Рис. 43
Рис. 43
Пример задачи 10
Построить фронтальную проекцию линии пересечения конической и торовой оболочек, имеющих общую плоскость симметрии, параллельную V (рис. 44).
Анализ данных. Оси поверхностей не пересекаются,  . Поверхности имеют общую плоскость симметрии, параллельную
. Поверхности имеют общую плоскость симметрии, параллельную  .
.
Анализ решения. Анализ данных говорит о том, что есть предпосылки для использования метода вспомогательных сфер. Если через любое круговое сечение поверхности одной оболочки можно провести сферу, пересекающую другую оболочку также по окружности, то можно применить для решения метод эксцентрических сфер. При решении другими способами пришлось бы строить лекальные кривые.
Алгоритм решения.
1. Пересекаем торовую поверхность фронтально-проецирующей плоскостью  , проходящей через ось тора. Линия пересечения – окружность, которая проецируется на
, проходящей через ось тора. Линия пересечения – окружность, которая проецируется на  1 в отрезок (1″, 2″).
1 в отрезок (1″, 2″).
2. Из середины отрезка (1″, 2″) – точки  восставляем перпендикуляр к плоскости окружности (1,2) и отмечаем точку
восставляем перпендикуляр к плоскости окружности (1,2) и отмечаем точку  его пересечения с осью конической оболочки.
его пересечения с осью конической оболочки.
3. Из точки  проводим сферу радиусом, равным отрезку
проводим сферу радиусом, равным отрезку  I”. Эта сфера пересечет торовую поверхность по окружности 1,2, а коническую – по окружности 3,4, фронтальная проекция которой – отрезок 3″ – 4″.
I”. Эта сфера пересечет торовую поверхность по окружности 1,2, а коническую – по окружности 3,4, фронтальная проекция которой – отрезок 3″ – 4″.
4. Отмечаем точку A” = [1″2″]  [3″4″], получится точка A
[3″4″], получится точка A  l, где l =
l, где l =  . Аналогично определяем точки B” и C” с помощью плоскостей
. Аналогично определяем точки B” и C” с помощью плоскостей  и
и  . Точки D” и E” находятся пересечением очерковых образующих поверхностей.
. Точки D” и E” находятся пересечением очерковых образующих поверхностей.
 Рис. 44
Рис. 44
Возможно, вас также заинтересует эта ссылка:
Варианты задания № 5
Варианты 1-10. Фреза, вращаясь вокруг оси, перемещается в направлении b . Ее конечное положение определяется точкой O2. Построить проекции выемки, получаемой при обработке фрезой подвижной детали.
Варианты 11-13. Построить на чертеже проекции границы зоны набольших силовых и тепловых нагрузок на корпус летательного аппарата при работе реактивного двигателя (линия пересечения поверхности струи с корпусом). Сопло – круговой конус. Поверхность струи – поверхность вращения, фронтальный очерк которой изображен на чертеже.
Варианты 14-19. Изобразить на чертеже горизонтальную и фронтальную проекции крышки сопла реактивного двигателя – части цилиндрической поверхности корпуса, ограниченной линией пересечения сопла с поверхностью корпуса. Сопло – круговой конус с углом при вершине  . Угол между осью цилиндрического корпуса и осью сопла
. Угол между осью цилиндрического корпуса и осью сопла  . Толщиной материала пренебречь.
. Толщиной материала пренебречь.
Вариант 20. Построить фронтальную проекцию вырезов на корпусе громкоговорителя (линия пересечения конической поверхности и цилиндрической горизонтально-проецирующей поверхности). Изобразить только видимые части вырезов.
Варианты 21-22. Построить фронтальную проекцию рукоятки.
Варианты 23-24. Построить линии пересечения на корпусе электропневмоклапана.






Тема 6. Развертки технических форм
Цель – выработать навыки построения разверток технических форм.
Под разверткой подразумевается преобразование, в результате выполнения которого все точки поверхности совмещаются с плоскостью. Развертываться могут только линейчатые поверхности, смежные прямолинейные образующие которых пересекаются в собственной или несобственной точках. Общий алгоритм построения разверток кривых поверхностей можно сформулировать так: заданная поверхность заменяется, аппроксимируется другой поверхностью, которая вписана или описана около нее и является развертывающейся поверхностью. Если кривая поверхность линейчатая, то она аппроксимируется пирамидальными и призматическими поверхностями, а если криволинейная (с кривыми производящими), то обычно она аппроксимируется такими развертывающимися поверхностями, как конусы и цилиндры (хотя встречается аппроксимация и гранными поверхностями), которые, в свою очередь, тоже заменяются гранными поверхностями, а последние уже развертывают.
Для построения разверток используется один из трех способов: раскатки, нормального сечения, треугольников (триангуляция). Способ раскатки рекомендуется при построении развертки призматических и цилиндрических поверхностей, одно из оснований которых, а также ребра или образующие параллельны каким-либо плоскостям проекций. Если основания поверхностей не проецируются на одну из плоскостей без искажения, то для построения развертки рекомендуется применять способ нормального сечения. Сущность способа треугольников состоит в том, что кривая поверхность аппроксимируется гранной, с треугольными гранями, и строится развертка гранной поверхности, состоящей из истинных величин треугольников.
Чертежи разверток широко применяются при изготовлении изделий из листового материала в судостроении, в котельном, кровельном, жестянном, картонажном и других производствах. В инженерной практике часто встречаются технические поверхности, представляющие собой комбинации различных развертывающихся и неразвертывающихся поверхностей. При построении их разверток в каждом конкретном случае необходимо пользоваться тем способом, который дает наиболее точный результат. Чтобы полностью решить задачу построения развертки поверхности, следует определить вид поверхности отдельных элементов изделия и построить их линии пересечения, выбрать способ построения разверток элементов изделия, построить развертку поверхности отдельного элемента или всего изделия.
Пример задачи 11
Построить развертку воздухозаборника, поверхность которого задана двумя направляющими: прямой AB и полуокружностью CD и плоскостью параллелизма W . Производящая – прямая линия (рис. 45).
Анализ данных. Заданная поверхность – коноид. Она относится к линейчатым неразверты-ваемым поверхностям, так как развертываться могут только линейчатые поверхности, смежные прямолинейные образующие которых пересекаются. Здесь смежные образующие скрещиваются.
Анализ решения. Произвольная образующая коноида строится легко благодаря тому, что мы знаем положение плоскости параллелизма. Построим приближенную развертку способом треугольников. Для этого аппроксимируем поверхность коноида многогранной поверхностью с треугольными гранями и строим развертку многогранника.
Алгоритм решения:
- Проводим ряд образующих коноида [1,4] // [2,5] // [3,6] // W, чем разобьем поверхность на четырехугольники. Чем больше мы возьмем образующих, тем точнее будет развертка.
- Проводим диагонали [1,A],[1,5],[3,5], которые разбивают поверхность на треугольники C – A -1, A -1 – 4, 415, 512, 523, 536, и таким образом аппроксимируем поверхность многогранной поверхностью с треугольными гранями.
- Строим развертку многогранной поверхности. Для этого необходимо знать истинные величины ее ребер. Большинство из них занимает частное положение относительно плоскостей проекций, поэтому их истинную величину можно снять непосредственно с чертежа (например [1 – 4] = [1- 4″‘]). Общее положение занимают [A,1], [1,5], [5,3], истинные величины которых могут быть найдены способом прямоугольного треугольника (рис. 45). Плавно соединив точки, лежащие на направляющих, получим половину приближенной развертки. Полную развертку легко построить зная, что (3 – 6) – ось симметрии.

Рис. 45
Пример задачи 12
Построить развертку конического патрубка тройника (рис. 46).
Анализ данных. Оси патрубков пересекаются. Все три поверхности описаны около сферы, следовательно, линия их пересечения согласно теореме Монжа распадается на кривые второго порядка, плоскости которых проходят через прямые, соединяющие точки пересечения линий касания.
Анализ решения. Для построения развертки, достроим коническую поверхность так, чтобы появилось нижнее основание, перпендикулярное к оси вращения. Развернем усеченный конус на плоскость. Применим так называемый способ трапеции, так как вершина конуса недоступна. Затем нанесем на развертке образующие и отметим на них точки, принадлежащие линиям пересечения, для чего определим истинные величины отрезков образующих вращением вокруг оси конуса.
Алгоритм решения:
- Достраиваем конус. Для этого из точки K” проводим прямую, перпендикулярную оси конуса, до пересечения с очерковой образующей конуса. Строим горизонтальную проекцию усеченного конуса.
- Проводим образующие конуса [1,2]; [3,4]; [5,6]; [7,5], равноотстоящие друг от друга.
- Строим развертку дополненного усеченного конуса. Для этого строим трапецию 8 – 9 -10 -11, у которой основания равны длинам окружностей оснований конуса (можно построить, аппроксимируя окружность хордами), а высота равна образующей конуса. Из вершин 8 и 9 проводим перпендикуляры к [8,9] до пересечения с осью симметрии. Делим пополам отрезки [13 -15] и [12 -16]. Соединяем плавной кривой точки 9 -14 -10 и 8 -17 -11.
- Наносим на развертку образующие.
- Наносим на образующие точки A, B, C, D, E, F, G , определив вращением вокруг оси конуса их истинное положение (рис. 46). Вторую половину развертки легко построить, зная, что 15-12 – ось симметрии.
 Рис. 46
Рис. 46
Варианты задания № 6
Варианты 1-2. Построить развертку оболочки, образованной перемещением прямолинейной производящей по криволинейным направляющим AB и CDE. Плоскость параллелизма  , AB – полуокружность. Определить вид поверхности.
, AB – полуокружность. Определить вид поверхности.
Варианты 3-4. Построить развертку оболочки, образованной перемещением профильной прямой по направляющим AB и CD (полуокружность). Определить вид поверхности.
Варианты 5-6. Построить развертку оболочки, образованной перемещением горизонтальной образующей по направляющим AB и CD (полуокружность).
Вариант 7-12. Подобрать геометрические характеристики конического (цилиндрического) патрубка или цилиндрического трубопровода так, чтобы пересечение происходило по плоским кривым. Построить развертку помеченной * поверхности.
Вариант 13-22. Построить развертку цилиндрического (конического) патрубка или участка трубопровода.
Вариант 23. Построить развертку конического элемента (помечен звездочкой), регистрирующего пера чернильного самописца.
Вариант 24. Построить развертку конического сопла.






Оформление индивидуальных графических заданий
Каждое индивидуальное задание выполняется на отдельном листе чертежной бумаги, формат которого студент выбирает самостоятельно, чтобы исходный чертеж и решение разместились на поле чертежа, исходные данные и графическое решение были четкими и понятными, а формат заполнен построениями. Среди установленных стандартом форматов в учебном процессе чаще всего используются два, которые обозначаются А3 и А4 с размерами сторон соответственно 297х420; 210х297.
На чертеже наносится обрамляющая линия (линия рамки) на расстоянии 5 мм от линии обрезки в направлении поля чертежа для форматов A3 и А4 и на расстоянии 5.. .10 мм для остальных форматов. Толщина на обрамляющей линии не менее 0,7 мм. На всех чертежах предусмотрено поле подшивки размером не менее 20х297 мм (рис. 47).

Рис. 47
Основная надпись размещается по обрамляющей линии в правом нижнем углу поля чертежа для формата А4 по короткой стороне, а для А3 – как по длинной, так и по короткой. В правом верхнем углу помещают индивидуальное задание. Исходный чертеж, следует увеличить по сравнению с заданием согласно указаниям. Надо помнить, что масштабы изображений регламентируются ГОСТ 2.302-68. При выполнении учебных графических работ чаще всего встречаются следующие масштабы: натуральная величина 1:1, масштабы уменьшения 1:2; 1:2,5; 1:4; 1:5, масштабы увеличения 2:1; 2,5:1; 4:1; 5:1.
Все графические построения выполняются с максимальной точностью и только с помощью чертежных инструментов. Для выделения желательно применять цветные карандаши. Надписи выполняются чертежным шрифтом по ГОСТ 2.304-68. Изображения выполняются сплошными основными линиями толщиной S = 0,6…0,8 мм. Линии связи и вспомогательные построения выполняются сплошными тонкими линиями толщиной S/2 – S/3 (ГОСТ 2.303-68).
Все построения необходимо сохранить, а также обозначить проекции точек, линий и т.д. После того как задача решена и решение оформлено, следует заполнить основную надпись. Пример заполнения основной надписи приведен на рис. 48.

Рис. 48
Возможно, вас также заинтересует эта ссылка:
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа №7 г. Няндома»
ОБРАЗОВАТЕЛЬНЫЙ ПРОЕКТ
Тема: «Решение задач по готовым чертежам как одно из эффективных средств для успешной сдачи ГИА».
разработала: Жигарева Анастасия Владимировна
учитель математики
МБОУ СШ № 7
г. Няндома, 2017г.
Введение.
Геометрия полна приключений,
потому что за каждой задачей
скрывается приключение мысли.
Решить задачу – это значит
пережить приключение.
(В. Произволов)
Какие задачи по математике считаются самими трудными? Думаю, что большинство учеников и педагогов ответят, что геометрические. Так как для решения типовых алгебраических задач применяются алгоритмы решения и проблемы, которые возникают при их решении, носят в основном вычислительный характер. А при решении геометрических задач нет единых алгоритмов и большинство ребят сталкиваются с трудностями. С чего начинать? Как решать? На что опираться? Надо знать аксиомы, а из большого списка теорем уметь выбирать необходимую, это сделать не так просто.
При решении геометрических задач многие обучающиеся сталкиваются с трудностями: ученику иногда легче решить задачу, чем сделать к ней чертеж. Решение задач по готовым чертежам способствует активизации мыслительной деятельности обучающихся, развивает речь, логику рассуждений, учит делать правильное выводы; дает возможность учителю повторить значительно больший объем материала, затратив при этом минимум времени.
Тему работы: «Решение задач по готовым чертежам как одно из эффективных средств для успешной сдачи ГИА» я выбрала, так как, проанализировав результаты ОГЭ по математике за последние три года в нашей школе, пришла к выводу, что одной из причин, по которой обучающийся может получить неудовлетворительную оценку на экзамене по математике – это невыполнение или неверное решение задач модуля «Геометрия».
В данной работе я рассмотрела некоторые задания решений задач по готовым чертежам, составленные с условием дифференциации. Предлагаемые упражнения не ставят целью заменить систему задач учебника, а являются лишь дополнением к ней. Они дают возможность учителю сэкономить значительную часть времени на изучение соответствующих тем и способствуют усилению практической направленности преподавания геометрии.
Актуальность проекта.
Современное общество понимает важность математического образования подрастающего поколения, признает его необходимость. Математика является обязательным предметом на всех этапах школьного обучения с 1 по11 класс, экзамен по математике является обязательным и в 9, и в 11 классах. Многие годы проверке подлежала алгебраическая подготовка выпускников, геометрия относилась к числу экзаменов «по выбору», и это был устный экзамен. В настоящее время в рамках ГИА по математике проводится проверка знаний и по алгебре, и по геометрии. Задачи по геометрии занимают примерно третью часть всех заданий КИМов ГИА. Решение задач по геометрии вызывает затруднения у многих обучающихся. Поэтому обучение поиску способов решения геометрических задач и организация учебно-познавательного процесса обучающихся всегда была и остается актуальной проблемой.
Как помочь каждому школьнику справиться с заданиями ГИА, а учителю эффективнее организовать учебный процесс?
Частичный выход из этого положения видится в использовании готовых чертежей для решения геометрических задач.
Цель проекта: применение задач на готовых чертежах в учебном процессе с целью повышения качества знаний, умений и навыков обучающихся.
Задачи проекта:
– изучить и кратко изложить основные теоретические вопросы по теме проекта;
– повысить интерес и мотивацию учеников к изучению геометрии;
– разработать сборник упражнений для решения задач по готовым чертежам (по уровням сложности);
– повысить эстетическую привлекательность урока;
– проанализировать опыт использования разработанных материалов в практике преподавания.
Объект проекта:
Обучающиеся 7-9 классов МБОУ СШ № 7
Ресурсное обеспечение для реализации проекта: Материально-технические: класс с мультимедией. Информационные: комплекты дидактических материалов (таблицы, раздаточный материал); электронные пособия по математике, обучающие компьютерные презентации.
Реализация проекта: 2015-2020 гг.
Этапы проекта:
1. Подготовительный этап (2015-2016 уч.год)
-проведение диагностической работы и ее анализ (Приложение 1);сбор и обработка информации; формулировка проблемы; определение целей и задач; планирование уроков с решением задач на готовых чертежах; разработка системы оценки эффективности работы над проектом.
2.Основной этап (сентябрь 2016 г.- апрель 2020 г.)
-проведение уроков геометрии с использованием готовых чертежей при решении задач; создание сборника задач на готовых чертежах при подготовке к ГИА.
3. Заключительный этап (май 2020 г)
– диагностика обучающихся; анализ полученных результатов; обобщение опыта на заседании МО; оформление результатов; выпуск сборника задач на готовых чертежах при подготовке к ГИА.
Методы проекта:
-
анализ литературы;
-
наблюдение;
-
сравнительный анализ.
Предполагаемые результаты: повысится уровень подготовки обучающихся к экзамену, и вследствие этого улучшатся результаты сдачи ОГЭ по математике.
Гипотеза: использование на уроках геометрии задач по готовым чертежам дает возможность:
-
обучающимся быстро запомнить теоретический материал и развивать интерес к самостоятельному решению задач;
-
учителю повторить значительно больший объем материала, затратив при этом минимум времени.
Теоретические основы понятия «задача».
Что же такое задача? По Л.М. Фридману задача – это требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче.
Решение задач – это работа несколько необычная, а именно умственная работа. Для того, чтобы научить обучающихся решать задачи, надо помочь им разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Геометрическая задача – это ситуация, требующая от обучающихся мыслительных и практических действий. Хотя способы решения традиционных задач хорошо известны, но организация деятельности обучающихся по решению задач является одним из условий обеспечения глубоких и прочных знаний.
Решить геометрическую задачу – это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется найти в задаче – её ответ.
Методы и приёмы обучения решению геометрических задач.
Условно процесс обучения обучающихся решению геометрических задач можно разделить на следующие основные этапы:
1.Изучение теоретического материала, составление опорного конспекта.
2. Решение задач по готовым чертежам.
3. Решение ключевых задач.
4. Рассмотрение различных способов решения одной задачи.
5.Решение различных задач обязательного уровня.
6. Решение задач повышенного уровня, нестандартных задач.
На начальном этапе изучения геометрии, на мой взгляд, основную трудность для обучающихся представляет выполнение чертежей к задачам: одни неправильно выполняют построение, другие очень много времени тратят на его выполнение.
Я считаю, для того, чтобы устранить эти проблемы, на уроках нужно использовать задачи по готовым чертежам, но при этом не делать их основным элементом в уроке. Обучающиеся на уроках геометрии обязательно должны учиться строить, чертить с помощью линейки, циркуля геометрические фигуры. Им необходимо научиться чертить сложные и несложные элементы.
Но для правильного представления о структуре задачи можно предложить уже готовый чертеж.
На моих уроках геометрии каждое высказывание обучающегося сопровождается демонстрацией чертежа, причем чертеж и данные из условия находятся перед глазами учащихся в процессе решения задачи. Тогда обучающиеся не только читают условия задачи, но и воспринимают их визуально и, в результате, легче решают.
При выполнении таких упражнений происходит активная мыслительная деятельность обучающихся, что, в свою очередь, приводит к эффективному запоминанию определений, свойств и признаков изучаемых фигур. Все предлагаемые определения, свойства и признаки рассматриваемых фигур периодически повторяются в процессе выполнения разнообразных упражнений, что приводить в итоге к продуктивному запоминанию. Большое значение имеет и то, что обучающиеся с удовольствием предпочитают выполнять эти упражнения, чем отвечать на вопросы теоретического материала.
Основные цели работы с готовыми чертежами:
– помощь обучающимся в усвоении и закреплении новых понятий и теорем;
– повторение и усвоение значительный объём материала за минимум времени;
– активизация мыслительной деятельности обучающихся;
– обучение грамотному рассуждению, нахождению в чертежах общего и отличительного, составлению и противопоставлению, формулированию правильных выводов;
– повышение творческой активности обучающихся;
– развитие логического мышления обучающихся.
Описание видов работ с чертежами.
1.Чертежи можно использовать для устного решения задач. (Приложение 2.1)
Например, в начале урока 10 – 15 минут, как повторение пройденного материала. Или для создания у обучающихся ситуации успеха при подготовке к усвоению нового материала (подготовительный этап).
В таких задачах на карточке уже четко записано условие задачи, для нахождения ответа, как правило, не хватает одного элемента. Обучающиеся:
– восстанавливают словесно условие задачи;
– показывают данные элементы, проговаривая условие, помечают их дополнительно на чертеже;
– найдя устно неизвестный компонент в задаче, проговаривают свойство, на которое они опирались при решении.
2. Задачи можно использовать для частичного оформления в тетрадях.(Приложение 2.2)
Для работы берутся задачи обязательно с условием, в которых неизвестны два элемента.
Можно составлять план нахождения без вычислений.
А можно вычислить только промежуточный результат, записывая результат вычисления.
Почему действовали именно так, обучающиеся проговаривают устно.
3. Задачи можно использовать для полного решения с объяснением в рабочих тетрадях. (Приложение 2.3)
При этом чертеж переносить не нужно.
а) Здесь можно использовать задачи без условия: обучающиеся учатся по чертежу находить и восстанавливать условие задачи и самостоятельно строить вопрос. Работу над такими чертежами следует начинать, когда полностью усвоен теоретический материал.
б) Также можно использовать задачи с условием, но обучающиеся полностью записывают решение с подробными выводами, при этом чертеж не восстанавливают в тетрадях.
4) Чертежи можно использовать при зачётах.(Приложение 2.4)
При этом обучающиеся могут выбирать по желанию чертеж и работать с ним.
Можно заранее дать набор таблиц и поставить перед обучающимся задачу проанализировать и сделать выводы.
5) Готовые чертежи можно использовать при работе в парах.
При этом осуществляется контроль обучающихся своих знаний и умений.
Обучающиеся обсуждают, делают выводы и учатся находить ошибки друг у друга.
Проработав несколько лет по данной методике, я пришла к выводу, что, на мой взгляд, данные упражнения быстро готовят обучающихся к запоминанию и самостоятельному решению задач, учат выделять из задачи главные и второстепенные элементы, после твердого усвоения материала позволяют составлять обратные задачи.
Задачи на готовых чертежах я использую как дополнительный материал к уже созданной системе задач курса геометрии 7- 9 класса.
В данной работе мне хочется рассмотреть систему упражнений на готовых чертежах по теме «Признаки равенства треугольников», которые я предлагаю обучающимся после изучения всех признаков равенства треугольников.
1. Найдите равные треугольники, пользуясь первым признаком равенства треугольников (рис.1).  рис.1
рис.1
2. Пользуясь вторым признаком равенства треугольников, выберите равные треугольники (рис. 2, а-г).
3. Пользуясь третьим признаком равенства треугольников, выберите равные треугольники (рис. 3, а-г).
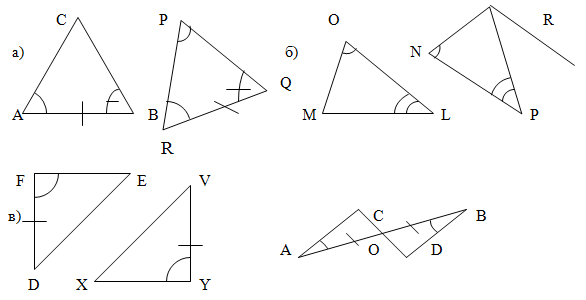 рис.2
рис.2
-
Можно ли утверждать, что:
а) ![]() (рис.1, а); б)
(рис.1, а); б) ![]() (рис.1, б);
(рис.1, б);
в) ЕК=ОР (рис. 1, в); г) DE=VX (рис.2, в);
д) ![]() (рис.2, г); е)
(рис.2, г); е) ![]() (рис.3, а);
(рис.3, а);
ж) AB=A1B1 (рис.3, б); з) ![]() (рис.3, в)?
(рис.3, в)?
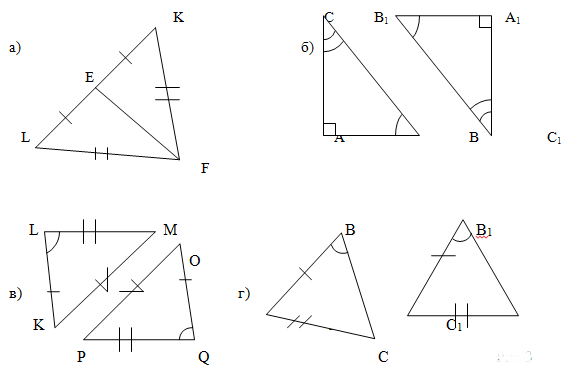 рис.3
рис.3
5. Укажите равные треугольники, пользуясь признаками равенства треугольников (рис. 4).
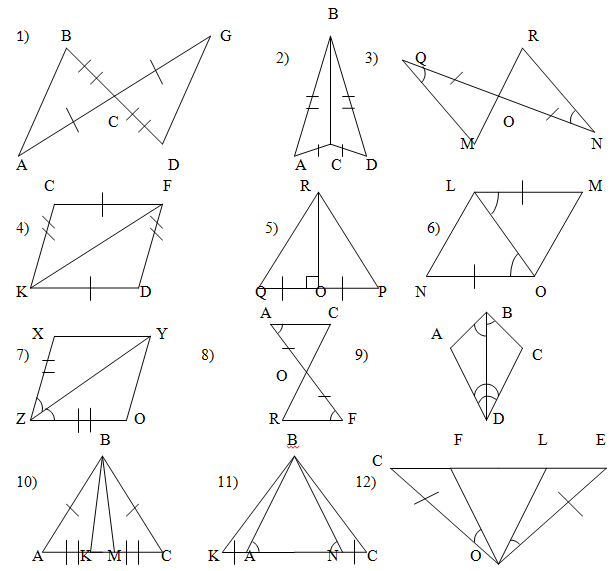 рис.4
рис.4
После выполнения упражнений 1–3 на готовых чертежах, учитель может легко диагностировать уровень сформированности учебных действий у обучающихся. Если они не выбрали случай г в первом упражнении, случаи а и г во втором и случаи а и в в третьем, то это свидетельствует о не сформированности действия распознавания ситуаций, удовлетворяющих соответственно первому, второму и третьему признаку равенства треугольников.
Если при выполнении упражнения 4 обучающиеся допускают ошибки, то это свидетельствует о том, что не сформировано действие преобразования заключения теоремы и действие осмысления связей между элементами задачи.
В результате выполнения упражнения 5 обучающиеся распознают равные треугольники, применяя самостоятельно один из необходимых признаков, оперируют свойствами равнобедренного треугольника, свойствами смежных и вертикальных углов.
Верное выполнение обучающимися всех заданий свидетельствует о сформированности у них умения применять знания в новой, видоизменной ситуации, используя общелогические и эвристические действия, приемы. Данные упражнения направлены на наглядное восприятие признаков равенства треугольников, формирование целостной системы знаний и умений по данной теме геометрии. Они способствуют своевременному выявлению отклонения в сформированности действий, адекватных изучению понятий и теорем, и внесению корректив и изменений в процесс обучения.
На первом этапе проекта (первый год моей работы в школе, 2015г.) мною была проведена диагностическая работа обучающихся 8 В класса, результаты которой были очень низкие (Приложение 1). Планируется провести аналогичную работу в декабре 2017 года уже с обучающимися 8 Б класса, с целью промежуточной проверки данной методики. Предполагаю, что результаты должны быть выше.
На данный момент проект реализуется на основном этапе. Мною разрабатывается сборник задач на готовых чертежах при подготовке к ГИА (Приложение 3). Проведение уроков геометрии с использованием задач по готовым чертежам применяются мною в школе третий год (с 2015г). Большинство ребят уверенно решают задачи по готовым чертежам, приводят обоснованные ответы и могут успешно применять их как элементы содержательных задач. Внешний мониторинг качества образования в 9-м классе (результаты основного государственного экзамена) показал, что все обучающиеся (26 чел.) справились с геометрическими задачами базового уровня. Выявлено, что для 63% ребят методика проведения уроков с использованием упражнений на готовых чертежах помогла в освоении программного материала по геометрии. Это позволило мне убедиться в эффективности данной методики.
На мой взгляд, методика проведения уроков с использованием упражнений на готовых чертежах развивает пространственное воображение, способствует активизации мыслительной деятельности обучающихся, развивает речь, память, логику рассуждений, учит делать правильные выводы, а значит является эффективным средством усвоения и закрепления теоретического материала по геометрии.
Заключение
Процесс изучения геометрии включает самые разнообразные виды деятельности. И в первую очередь – решение задач. Задача – это не только умения, это и элемент знания. В решении задач есть определенный азарт. Решение геометрических задач как ничто другое заставляет мыслить, рассуждать, а значит, развивает логическое мышление, сообразительность, способствует уровню математической грамотности. Научить решать обучающихся геометрические задачи – это значит не только подготовить их к хорошей сдаче экзамена, но и научить обучающихся доказательно отстаивать свою точку зрения, уметь творчески подходить к любому делу.
Успех обучения геометрии в определенной мере зависит от того, какие задачи, в какой последовательности, и в каком количестве даются обучающимся для работы на уроке и дома. Поэтому при организации процесса обучения обучающихся решению геометрических задач учитель в первую очередь сталкивается с необходимостью отбора задач, их упорядочивания, анализа тех умственных действий, которые должны будут выполнить обучающиеся в процессе решения задач.
Список литературы и интернет-ресурсов:
-
Э. Балаян Геометрия. Задачи на готовых чертежах для подготовки к ГИА и ЕГЭ 7-9 классы/ Ростов-на-Дону: Феникс, 2012
-
Н.Ф. Гаврилова Универсальные поурочные разработки по геометрии: 9 класс. М.:ВАКО, 2010, 320с.
-
Крымская Ю. А., Ячинова С. Н. Роль упражнений на готовых чертежах в процессе обучения решению геометрических задач // Молодой ученый. — 2014. — №17. — С. 498-501
-
Н.В.Доброва, статья «Решение задач по готовым чертежам – одно из эффективных средств усвоения и закрепления теоретического материала по геометрии», 2016г.
https://infourok.ru/reshenie-zadach-po-gotovim-chertezham-odno-iz-effektivnih-sredstv-usvoeniya-i-zakrepleniya-teoreticheskogo-materiala-po-geometri-2021556.html
-
М. Н. Кондакова, статья «Описание работы на уроках геометрии по готовым чертежам»,2015г. https://nsportal.ru/blog/shkola/matematika/all/2015/02/07/opisanie-raboty-na-urokakh-geometrii-po-gotovym-chertezham
6.https://oge.sdamgia.ru/
В современной начальной школе требования к оформлению задачи несколько отличаются от привычных родителям. Стало обязательным использование схем в виде одного или нескольких отрезков, на которых отображаются данные и неизвестное. Иногда сложность у ребенка вызывает именно решение задачи с использованием схемы.
Суть схем в том, чтобы по условию задачи определить, что за тип схемы ей соответствует, и найти решение с использованием этой схемы. Такой подход помогает упростить решение текстовых задач в старших классах и составление системы уравнений.
В этой статье мы проиллюстрируем все схемы к математическим задачам, а потренироваться определять схему и подготовиться к решению задач вы сможете на тренажере.
Задачи на нахождение суммы
У Максима было 4 яблока и 3 груши. Сколько всего было фруктов у Максима?
Задачи на увеличение и уменьшение числа на несколько единиц
У Иры 8 карандашей, а у Коли – на 8 больше. Сколько карандашей у Коли?
Задачи на нахождение неизвестного слагаемого
У Васи было 10 рублей. Два рубля он потратил на леденец, а остальные – на жвачку. Сколько рублей Вася потратил на жвачку?
Задачи на нахождение остатка
У Юры было 10 конфет, 8 конфет Юра раздал друзьям . Сколько конфет осталось у Юры?
Задачи на нахождение неизвестного вычитаемого и слагаемого
У Петиной кошки родилось 9 котят. Когда Петя раздал несколько котят знакомым, у него осталось 6 котят. Сколько котят раздал Петя?
Задачи на разностное сравнение
У Маши было 8 комиксов, а у Наташи – 5. На сколько комиксов больше у Маши, чем у Наташи?
Задачи с косвенными вопросами
Бабушка сварила 7 банок малинового варенья, что на 2 банки меньше, чем абрикосового варенья. Сколько банок абрикосового варенья сварила бабушка?
Составные задачи на нахождение суммы
Папа купил 3 килограмма леденцовых конфет, а шоколадных конфет на 2 кг больше. Сколько всего килограмм конфет купил папа?
Составные задачи на нахождение остатка
Лене задали решить 3 задачи на сложение и 5 задач на вычитание. После решения 6 задач, Лене осталось сделать еще несколько. Cколько задач осталось решить Лене?
Составные задачи на нахождение слагаемого и вычитаемого
У Вити было 5 игрушечных гоночных машин и 4 обычных игрушечных машины. Несколько машин Витя подарил Толе, и у Вити осталось 6 машин. Сколько игрушечных машин Витя подарил Коле?
Составные задачи на нахождение третьего слагаемого
На трех грядках росли свекла, редис и морковь. С трех грядок хозяйка собрала 60 овощей. С двух грядок получилось 10 свекл и 20 редисок. Сколько морковок собрала хозяйка?
Составные задачи на нахождение уменьшаемого
Из мешка с подарками Дед Мороз достал 3 куклы и 2 набора Лего. Сколько всего подарков было у Деда Мороза в мешке, если в нем осталось 3 мягких игрушки?
Д.А.Сафронов, учитель математики
Роль чертежа в решении геометрических задач.
В решении геометрических задач,безусловно, важную роль играет чертёж. О роли чертежа в решении задач написаны масса статей и диссертаций. Так, в работе (1) раскрывается, что правильно составленный чертёж может подсказать идею решения задачи. Полностью согласен с утверждением авторов, что крайности, как-то: отсутствие чертежа, как такового, или небрежное его исполнение, негативно сказываются на ход решения большинства задач, впрочем, как и обоснование каких-либо неверных фактов, сделанных на основе выполненного чертежа. В некоторых работах, например, (2), рекомендуется делать очень точные чертежи, чуть ли не в масштабе и разными цветами. Такой чертёж, дескать, помогает анализировать задачу, выдвигать гипотезы ее решения и проверять ее решения. В идеале, конечно, так решать задачи можно. Однако, во-первых, на хороший чертёж всегда тратится масса времени, которое не всегда есть. Во-вторых, часто для решения задачи достаточно небольшого эскиза. Если исходить из принципа «достаточности», то не совсем понятно, каким образом сделать чертёж так, чтобы, с одной стороны, он помог решению задачи, а с другой, не перегружать его излишней, и, тем более, неверной информацией.
Разумную попытку ответить на этой вопрос я встретил лишь в работе (3), не претендующей на научные изыскания, а написанную, я так понял, на основе обобщения опыта автора. Все чертежи автор условно разбивает на «ужасные», где имеются факты (свойства фигур), противоречащих условию задачи; «плохие», где, наоборот, помимо заданных в задаче условий, есть и другие, не заданные в условии факты, использование которых может привести к ошибке и «хорошие», в которых, кроме всех заданных в условии фактов, нет ничего лишнего. Так как же сделать такой вот «хороший» чертёж?
Покажем вначале это на примерах.

Выделяем объект (геометрическую фигуру) задачи: параллелограмм. Производим чертёж параллелограмма. Не ромба, с равными сторонами, не прямоугольника, с прямыми углами, а именно параллелограмма. Обозначаем вершины. Согласно правилам, обозначать многоугольники можно как по часовой стрелке, так и против неё, однако порядок букв при этом необходимо сохранять. Согласно условию задачи, проводим из точки N к стороне MQ перпендикуляр NH и смотрим, выполняется ли условие задачи, что точка Н лежит на стороне MQ. Если лежит, обозначаем квадратиком прямой угол MHN, угол MNH, равный 30°, и подписываем длины известных отрезков, MH и HQ. Чертёж готов. Ни одно из условий задачи не пропущено, никаких дополнительных фактов в чертёж не внесено. Получилось примерно следующее:

На чертеже сразу виден прямоугольный треугольник с катетом 3 см, лежащий напротив угла 30°.Вспоминаем, что в этом случае гипотенуза равна удвоенному катету, т.е. 6 см. Смежная сторона MQ параллелограмма легко находится, как сумма отрезков MH и HQ, т.е. 8 см. Противоположные стороны параллелограмма равны, поэтому NP=8см, PQ=6см. Со сторонами разобрались.
Угол NMH ищется из того же прямоугольного треугольника MNH, по свойству прямоугольных треугольников: 90°-30° = 60°. Угол MNP находится, как сумма углов MNH и HNP, из которых он состоит, как видно из чертежа. ∠MNP = 30°+90° = 120°. Противоположные найденным углы параллелограмма равны соответственно также 120° и 60°. Задача решена.
Теперь давайте посмотрим, не поменяется ли решение задачи, если чертёж будет немного другим. Для начала проверим, что изменится, если обозначать вершины параллелограмма мы будем не по часовой, а против часовой стрелки. Последовательно отмечая аналогичным описанному выше способом все элементы чертежа, получаем примерно следующее:

Как видно из чертежа, практически ничего не поменялось, отчётливо виден всё тот же прямоугольный треугольник, на свойствах которого и основывалось решение задачи.
Какие есть ещё варианты изображения чертежа? А что будет, если обозначения будут начинаться не с острого, а с тупого угла параллелограмма? Понять это поможет следующий чертёж:

На данном рисунке нанесена не вся информация задачи, так как проведя из вершины N перпендикуляр, мы уже видим, что он попадает не на сторону MQ параллелограмма, а на её продолжение, что противоречит условию задачи. Значит, это- неверный вариант чертежа, и такой случай рассматривать не нужно. Таким образом, задача имеет единственное решение, приведённое к рисунку N1.
Ещё одна задача.

Речь снова идёт о параллелограмме. В условии задачи нет обозначений вершин, поэтому от порядка обозначений решение задачи меняться точно не будет. Но всё же на чертеже вершины стоит обозначать буквами, так удобнее записывать решение задачи. Чертим параллелограмм (с разными смежными сторонами), проводим биссектрису, дугами обозначаем равные углы, подписываем известные длины отрезков. Получаем рис.№4.

Чтобы найти периметр, нам достаточно вычислить длину стороны АВ. Рисунок подсказывает нам, что так как прямые АD и ВС параллельны, то ∠ ВКА = ∠ DАК (накрест лежащие). Обозначив его такой же дугой, видим равнобедренный треугольник АВК с боковыми сторонами АВ и ВК. Отметим это на чертеже, рис.№5:

Значит, АВ=14 см. и периметр параллелограмма будет равен 14*2+(14+7)*2=70(см).
Задача решена? Чтобы удостовериться в этом, проверим, изменится ли решение задачи, если биссектриса будет выходить не из острого, а из тупого угла. Получим чертёж, как на рис.№6.

Алгоритм решения задачи при этом не меняется, как не поменялись и исходные данные. Сторона АВ по-прежнему равна стороне АК равнобедренного треугольника. Получается АВ=14см. а периметр равен 70 см.
Какие могут ещё варианты чертежа? А что, если поменять местами длины отрезков? Такой вариант чертежа показан на рис.№7.

Чтобы соблюсти пропорции, сделаем стороны АD и ВС чуть длиннее. По уже найденному алгоритму видим равнобедренный треугольник, но с боковыми сторонами, равными АВ=ВК=7см ! Периметр параллелограмма с новыми длинами сторон будет равен 7*2+(14+7)*2=56(см.). Получаем второй ответ к задаче.
На основе приведённых примеров и личного опыта попробуем дать опредёлённые рекомендации к построению чертежей к геометрическим задачам.
1. Чётко идентифицировать объект ( геометрическую фигуру ), о котором идёт речь в задаче. Не наделять этот объект дополнительными характеристиками, которых нет в условии задачи ( Например, если речь идёт о треугольнике – не нужно чертить ни равнобедренный, ни прямоугольный треугольники)
2. Точный масштаб на чертеже соблюдать не обязательно, однако основные пропорции соблюдать желательно. Если в процессе выполнения чертежа какое-либо условие не может быть отражено, либо исказилось – чертёж следует переделать.
3. Обозначать буквами: вершины многоугольников, центры окружностей, точки пересечения прямых, отрезков и лучей, в том числе, если используются дополнительные построения. Если в условии задачи есть обозначения – использовать прежде всего их. Многоугольники обозначают «по кругу».
4. На чертеже также стоит обозначить все условия, данные в задаче: равные отрезки обозначить одинаковыми штрихами, равные углы – одинаковыми дугами, прямые углы – квадратиками. Подписывать длины известных отрезков.
5. Рассмотреть возможные альтернативные варианты выполнения чертежа. Проверить, не изменится ли условие, а, значит, и решение задачи, если чертёж будет соответствовать условию, но будет немного другим.
Если перечисленные рекомендации будут выполнены, чертёж действительно станет очень хорошим подспорьем в решении задачи и подскажет возможные пути её решения.
ЛИТЕРАТУРА
- Г. Дорофеев, Н. Розов, «Чертеж в геометрической задаче»,
Квант, 2020, номер 11-12, с.25–30
http://www.mathnet.ru/links/358d0017f644ec7a86faa8c8b738e26a/kvant1286.pdf
- Фалилеева М.В. «ТОЧНЫЕ ЧЕРТЕЖИ В ОБУЧЕНИИ ПЛАНИМЕТРИИ»// Современные проблемы науки и образования. – 2013. – № 2. – с. 250-250;
https://science-education.ru/ru/article/view?id=8653
- Стив Май «Хорошие чертежи в геометрии»
https://zen.yandex.ru/media/id/5cc82b9524de2d00b2ddcec7/horoshie-cherteji-v-geometrii-5dc37ec6c7e50c00adfc3ef5
На чтение 3 мин. Просмотров 205k.
Обновлено 12.08.2021
В этой ветке форума вы найдете основные типы задач для второго класса и схемы к ним. Теперь требования в начальной школе отличаются от тех требований, по которым учили нас в свое время. Раньше учили лишь записывать краткую запись, учителю важно было правильное решение и ответ. Теперь же обязательно требуется схема к задаче в виде одного или нескольких отрезков. На отрезках указываются данные и неизвестное.
Решение задачи у каждого ученика было по 3 ручки и 2 карандаша смотрите здесь
Содержание
- Задачи на нахождение суммы
- Задачи на увеличение уменьшение числа на несколько единиц
- Задачи на нахождение неизвестного слагаемого
- Задачи на нахождение остатка
- Задачи на нахождение неизвестного вычитаемого и слагаемого
- Задачи на разностное сравнение
- Задачи с косвенными вопросами
- Составные задачи на нахождение суммы
- Составные задачи на нахождение остатка
- Составные задачи на нахождение слагаемого и вычитаемого
- Составные задачи на нахождение третьего слагаемого
- Составные задачи на нахождение суммы
- Составные задачи на нахождение уменьшаемого
Задачи на нахождение суммы
У Сони было 4 синих карандаша и 3 коричневых. Сколько было всего карандашей у Сони?

Задачи на увеличение уменьшение числа на несколько единиц
Ване 8 лет, а его сестре – на 8 лет больше. Сколько лет сестре?

Задачи на нахождение неизвестного слагаемого
У кошки было 10 котят. 2 из них белого цвета, остальные — серого. Сколько серых котят было у кошки?

Задачи на нахождение остатка
.
У Вероники было 10 рублей. Она купила ручку за 8 рублей. Сколько денег осталось у Вероники?

Задачи на нахождение неизвестного вычитаемого и слагаемого
У Вики было 9 конфет. Когда несколько конфет Вика отдала друзьям, у нее осталось — 6. Сколько конфет подарила Вика?

Задачи на разностное сравнение
У Марины было 8 тетрадей, а у Маши — 5. На сколько больше тетрадей у Марины, чем у Маши?

Задачи с косвенными вопросами
Мама купила 7 кг вишни. что на 2 кг меньше, чем облепихи. Сколько кг облепихи купила мама?

Составные задачи на нахождение суммы
Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько всего фруктов купила хозяйка?

Составные задачи на нахождение остатка
Пете задали читать на лето 3 книги зарубежной литературы и 5 книг отечественной. После прочтения 6 книг, Пете осталось читать еще несколько. Cколько книг осталось прочитать Пете?

Составные задачи на нахождение слагаемого и вычитаемого
У кошки было 5 белых котят и 4 дымчатых. Когда несколько котят отдали, то их осталось 6. Сколько котят отдали?

Составные задачи на нахождение третьего слагаемого
Три друга – Миша, Саша и Ваня — получили за четверть 60 пятерок. Миша получил 10 пятерок, Саша – 20. Сколько пятерок получил Ваня?

Составные задачи на нахождение суммы
У Василисы 6 карамелек, шоколадных конфет на 4 меньше, мятных подушечек на 2 больше, чем шоколадных конфет. Сколько мятных подушечек у Василисы?

Составные задачи на нахождение уменьшаемого
Из пенала Витя взял 3 карандаша и 2 ручки. Сколько школьных принадлежностей в пенале было сначала, если в ней осталось 3 фломастера?

спасибо за схемы. но есть еще правила к схемам, а как они пишутся?
adoksana69, правил для составления схем нигде не видел. Нужно знать как, к каждому типу задач составляется схема. Ребенок справляется с заданием с помощью выработка навыка.
