Тригонометрия – это наука, изучающая свойства тригонометрических формул (trigwnon – треугольник и метр – мера).
Тригонометрич. формулы — это элементарные функции, выражающие зависимость всех сторон прямоугольного треугольника от острых углов к гипотенузе (или зависимость хорд и высот от его центрального угла в окружности).
К прямым функциям тригонометрии относятся: sin x (синус), cos x (косинус). К производным: tg x (тангенс), ctg x (котангенс). В дополнение к другим тригонометрическим функциям: sec x (секанс) и cosec x (косеканс).
Косинус и синус в тригонометрии — бесконечно дифференцируемые и периодически непрерывные вещественные функции. Остальные, наоборот, дифференцируются в области определения, однако, как и прямые тригонометрические функции, непрерывны.
Основные тригонометрич. тождества:
Зная синус или косинус числа, можно найти его тангенс или котангенс: tg a = sin a / cos a
Вы можете найти синус числа, если известен его косинус, и наоборот: sin2 a + cos2 a = 1
Можно найти тангенс через синус с известным косинусом: 1 + tg2 a = 1 / cos2 a
Вы можете найти котангенс через синус с известным косинусом: 1 + 1 / tg2 a = 1 / sin2
sin(90o – а) = cos а
cos(90o – а) = sin а
И еще, любую формулу в математике можно применять не только слева направо, но и наоборот. В тригонометрии это же применяется при преобразовании суммы в произведение или при переходе от произведения к сумме.
В данной статье мы с вами разберём некоторые задачи связанные с выражениями. Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.
Относительную сложность могут вызывать следующие:
— преобразования буквенных иррациональных выражений
— вычисление значений тригонометрических выражений
— преобразования тригонометрических выражений
Если перечислить все группы задач, то они довольно разнообразны.
Они включают в себя: ПОКАЗАТЬ/СКРЫТЬ
Здесь мы с вами разберём задачи на вычисление значений тригонометрических выражений. Конечно, все их в одной статье разобрать невозможно. Но мы обязательно разберём и другие примеры, не пропустите!
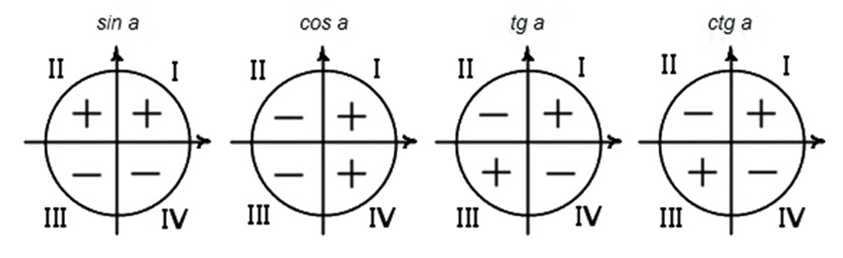
Итак, что обязательно вы должны знать и всегда помнить? Это знаки тригонометрических функций в четвертях. ЭТО ВАЖНО!!!
Как осознать эту информацию и понять следствием чего она является – об этом будет отдельная статья (если вы это знаете, то прекрасно). Пока предлагаю пока просто запомнить:
Основное тригонометрическое тождество:
Формулы тангенса и котангенса:
Выполняются элементарные алгебраические преобразования:
1. Числитель и знаменатель дроби можем умножать и делить на одно и тоже число.
2. Левую и правую часть уравнения можем умножать и делить на одно и тоже число.
В представленных ниже заданиях используется основное тригонометрическое тождество и формула тангенса.
Найдите тангенс альфа, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Косинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение синуса. Затем подставить их в формулу тангенса.
Теперь ВАЖНЫЙ момент: необходимо определить знак синуса для интервала (3Пи/2;2Пи). Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому:
Таким образом:
Ответ: – 0,5
Найдите tg α, если
В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:
Cинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение косинуса. Затем подставить их в формулу тангенса.
Определяем знак косинуса для интервала (Пи/2;Пи). Это интервал от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное (смотрите эскиз). Поэтому
Таким образом:
Ответ: – 0,25
Найдите 5·cos α, если синус альфа
Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos2x = 1– sin2x и
Определим знак косинуса. Угол принадлежит интервалу (3Пи/2;2Пи).
Это интервал от 270 до 360 градусов (четвёртая четверть). Значение косинуса в этой четверти положительное, поэтому:
Таким образом, 5·cos α = 5∙0,7 = 3,5
Ответ: 3,5
Найдите 0,1·sin α, если
Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin2x = 1– cos2x и
Определим знак синуса. Угол принадлежит интервалу (0; Пи/2).
Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:
Таким образом 0,1·sin α = 0,1∙0,3 = 0,03
Ответ: 0,03
Общая рекомендация для следующих данных примеров! Если требуется найти тангенс аргумента (квадрат тангенса), то осуществляем деление на косинус (квадрат косинуса). Если требуется найти котангенс аргумента (квадрат котангенса), то осуществляем деление на синус (квадрат синуса). Примеры:
65217. Найдите tg2 α, если 3sin2 α + 8 cos2 α = 7
Требуется найти квадрат тангенса. Разделим обе части уравнения на cos2 α, получим:
Второй способ:
Далее по формуле основного тригонометрического тождества можно найти квадрат синуса и используя формулу тангенса вычислить уже его квадрат:
Ответ: 0, 25
65269. Найдите
Преобразуем данное выражение так, чтобы в числителе и знаменателе был тангенс. Разделим числитель и знаменатель на cos α, получим:
Ответ: – 0,5
65273. Найдите
Здесь дано значение тангенса. Необходимо сделать так, чтобы в выражении у нас был тангенс. Вынесем cosα за скобки в числителе и знаменателе (или разделим числитель и знаменатель на cosα), получим:
Подставим значение тангенса данное в условии, получим:
*Косинус у нас сократился.
Ответ: 4
65363. Найдите tg α, если
В левой части в числителе и знаменателе вынесем cosα за скобки, получим:
Ответ: 0,4
65423. Найдите tg α, если
Умножим обе части уравнения на 4 (2sinα+cosα+1)
Ответ: –1,9
26775. Найдите tg α, если
Посмотреть решение
26776. Найдите tg α, если
Посмотреть решение
26777. Найдите 3cos α, если
Посмотреть решение
26778. Найдите 5sin α, если
Посмотреть решение
26787. Найдите tg2 α, если
Посмотреть решение
26788. Найдите
Посмотреть решение
26789. Найдите
Посмотреть решение
26790. Найдите tg α, если
Посмотреть решение
26791. Найдите tg α, если
Посмотреть решение
Подведём итог, для решения подобных примеров вы:
1. Должны знать на зубок основные формулы тригонометрии.
2. Не забывать определять знак (+ или -) для тригонометрических функций в четвертях. Потерянный знак на экзамене – это ошибка и потерянный бал, будьте внимательны!!!
Надеюсь, что материал был для вас полезен.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Попробуй так)) )
1
Для того, чтобы выразить тангенс угла через синус, нужно вспомнить геометрическое определение тангенса. Итак, тангенсом острого угла в прямоугольном треугольнике, называют отношение противолежащего катета к прилежащему.
2
С другой стороны, рассмотрите декартову систему координат, на которой начерчена единичная окружность с радиусом R=1, и центром О в начале координат. Примите поворот против часовой стрелки, как положительный, а в обратную сторону отрицательный.
3
Отметьте некую точку M на окружности. Из нее опустите перпендикуляр на ось Ох, назовите ее точкой N. Получился треугольник OMN, у которого угол ONM является прямым.
4
Теперь рассмотрите острый угол MON, по определению синуса и косинуса острого угла в прямоугольном треугольнике
sin(MON) = MN/OM, cos(MON) = ON/OM. Тогда MN= sin(MON)*OM, а ON = cos(MON)*OM.
5
Вернувшись к геометрическому определению тангенса (tg(MON) = MN/ON), подставьте полученные выше выражения. Тогда:
tg(MON) = sin(MON)*OM/cos(MON)*OM, сократите OM, тогда tg(MON) = sin(MON)/cos(MON).
6
Из основного тригонометрического тождества (sin^2(x)+cos^2(x)=1) выразите косинус, через синус:
cos(x)=(1-sin^2(x))^0,5
Подставьте это выражение в полученное на шаге 5. Тогда tg(MON) = sin(MON)/(1-sin^2(MON))^0,5.
7
Иногда существует потребность в вычисление тангенса двойного и половинчатого угла. Тут тоже выведены соотношения:
tg(x/2) = (1-cos(x))/sin(x) = (1-(1-sin^2(x))^0,5)/sin(x);
tg(2x) = 2*tg(x)/(1-tg^2(x)) = 2*sin(x)/(1-sin^2(x))^0,5/(1-sin(x)/(1-sin^2(x))^0,5)^2) =
= 2*sin(x)/(1-sin^2(x))^0,5/(1-sin^2(x)/(1-sin^2(x)).
8
Также возможно выразить квадрат тангенса через двойной угол косинуса, либо синус.
tg^2(x) = (1-cos(2x))/(1+cos(2x)) = (1-1+2*sin^2(x))/(1+1-2*sin^2(x)) = (sin^2(x))/(1-sin^2(x)).
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2πr. Следовательно 360° в радианах равно 2π, а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π.
Например, для угла 90° будет 90°180°· π = 12π
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Нахождение тангенса и котангенса через синус и косинус
[ tg alpha = dfrac{sin alpha}{cos alpha},enspace ctg alpha=dfrac{cos alpha}{sin alpha} ]
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой ( dfrac{y}{x}=dfrac{sin alpha}{cos alpha} ), а отношение ( dfrac{x}{y}=dfrac{cos alpha}{sin alpha} ) — будет являться котангенсом.
Добавим, что только для таких углов ( alpha ), при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества ( tg alpha = dfrac{sin alpha}{cos alpha} ), ( ctg alpha=dfrac{cos alpha}{sin alpha} ).
Например: ( tg alpha = dfrac{sin alpha}{cos alpha} ) является справедливой для углов ( alpha ), которые отличны от ( dfrac{pi}{2}+pi z ), а ( ctg alpha=dfrac{cos alpha}{sin alpha} ) — для угла ( alpha ), отличного от ( pi z ), ( z ) — является целым числом.
Видео
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде: tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению: tg α = y/x ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем
и
, получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Тангенс и косинус, котангенс и синус
Преобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам tg2α+1=1cos2α, 1+ctg2α=1sin2α.
Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби , где в числителе имеем 1, а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin2α+cos2α=1, можно разделить соответствующие стороны на cos2α и получить tg2α+1=1cos2α, где значение cos2α не должно равняться нулю. При делении на sin2α получим тождество 1+ctg2α=1sin2α, где значение sin2α не должно равняться нулю.
Из приведенных выражений получили, что тождество tg2α+1=1cos2α верно при всех значениях угла α, не принадлежащих π2+π·z, а 1+ctg2α=1sin2α при значениях α, не принадлежащих промежутку π·z.
Всё ещё сложно? Наши эксперты помогут разобраться Все услуги
Теги
Тригонометрические формулы
Тригонометрические формулы — элементарные функции, которые выражают зависимость всех сторон прямоугольного треугольника от острых углов при гипотенузе (или зависимость хорд и высот от его центрального угла в круге).

К прямым функциям тригонометрии относят: sin x (синус), cos x (косинус). К производным: tg x (тангенс), ctg x (котангенс). А также другие тригонометрические функции: sec x (секанс) и cosec x (косеканс).
Косинус и синус в тригонометрии являются Вещественнозначными функциями, которые неограниченно дифференцируются и являются периодически непрерывными. Остальные же наоборот дифференцируются в области определении, однако, как и прямые тригонометрические функции есть непрерывными.
Значения функция для некоторых углов представлены в следующей таблице. Обозначение «∞» говорит о том, что функция в данной точке не определена и стремится к бесконечности.
Основные тригонометрические тождества:
«То, что принято без доказательств, может быть отвергнуто без доказательств».
Евклид.
- При известном синусе или косинусе числа можно найти его тангенс или котангенс: tg a = sin a/cos a
- Можно найти синус числа, если известен его косинус и наоборот: sin2 a + cos2 a = 1
- Найти тангенс можно через синус при известном косинусе: 1 + tg2 a = 1/cos2 a
- Найти котангенс можно через синус при известном косинусе: 1 + 1/tg2 a = 1/sin2
- sin(90o – a ) = cos a
- cos(90o – a ) = sin a
Формулы двойного аргумента позволяют выразить sin2x, cos2x, tg2x через tg x, cos x и sin x. Соответственно формулы тройного аргумента выражают sin2x, cos2x, tg2x. Всем известно, что любая формула в математике может применяться не только слева на право, но и наоборот. В тригонометрии это действует во время преобразования суммы в произведение или же при переходе от произведения к сумме.
Переход от произведения к сумме:
Переход от суммы к произведению:

Возникновение тригонометрии и тригонометрических формул связанно с астрономией, строительным делом и землемерием. Не смотря на то, что некоторые факты и понятия были
известны еще две тысячи лет назад, сам термин тригонометрия появился относительно недавно. Впервые способ решать зависимости между сторонами треугольника нашли Гиппарх и Клавдий Птолемеи (ІІ н.е.). Только намного позже эти зависимости стали называть тригонометрическими формулами.



































 и
и  , получаем:
, получаем: 





