Как на круге найти четыре точки

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки “а” в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке “b”. Радиусом R3 из точки “1” проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние “b-О” даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки “1” окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала – традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним – нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части радиусами

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга – по факту, нарезка равных секторов. Метод и формулы очень просты:

1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

1. Определяем размер дуги сектора, перемножая радиус на угол в радианах

1. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё – мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x – это координата вдоль оси абсцисс, а y – это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Разметка окружностей, центров и отверстий. Деление окружности на равные части и построение многоугольников

При разметке все построения производятся с помощью двух линий — прямой и окружности (на рис. 3.42 с целью повторения представлены элементы окружности).

Рис. 3.42. Окружность и ее элементы

Нахождение центра окружности. На плоских деталях, где уже имеются готовые отверстия, центр которых неизвестен, его находят геометрическим способом. На торцах цилиндрических деталей нахождение центра производят при помощи циркуля, рейсмуса, угольника-цетроискателя и колокола.

Разметка центра по угольнику-центроискателю. Разметку выполняют в следующей последовательности.

• 1. Деталь устанавливают на разметочную плиту так, чтобы размечаемый торец был сверху.
• 2. На торец цилиндрической детали накладывают угольник-центроиска- тель так, чтобы две его стороны (планки) касались цилиндрической поверхности детали, рис. 3.43.

Рис. 3.43. Нахождение центра окружности с помощью угольника-центроискателя

• 3. Левой рукой плотно прижимают линейку угольника к поверхности торца, а правой проводят чертилкой первую диаметральную риску.
• 4. Угольник-центроискатель поворачивают по цилиндрической поверхности детали примерно на 90° и проводят вторую риску. Точка пересечения двух рисок будет центром размечаемой окружности.

Разметку центра детали с грубо обработанной цилиндрической поверхностью производят в такой же последовательности. В этом случае для более точного нахождения центра окружности необходимо нанести пять-семь рисок. Центром будет точка, в которой пересекается наибольшее число рисок.

Точность разметки центра окружности проверяют разметочным циркулем, рис. 3.44. Острие одной ножки циркуля устанавливают в размеченный центр, а другую ножку перемещают так, чтобы ее острие слегка касалось цилиндрической части детали. Если острие ножки циркуля касается по всей длине окружности, то центр размечен правильно.

Рис. 3.44. Способ проверки точности разметки центра окружности разметочным циркулем

Разметка центра рейсмусом (рис. 3.45). Деталь кладут на призмы или параллельные подкладки, уложенные на разметочную плиту. Устанавливают острый конец иглы рейсмуса несколько выше или ниже центра размечаемой

Рис. 3.45. Разметка центра рейсмусом

детали и, придерживая деталь левой рукой, правой рукой движением рейсмуса по плите прочерчивают его иглой на торце детали короткую рису. После этого поворачивают деталь на 1/4 окружности и таким же способом проводят вторую риску. То же повторяют через каждую четверть оборота для проведения третьей и четвертой рисок. Внутри рисок (на пересечении диагоналей) и будет находиться центр. Его набивают кернером.

Геометрический способ нахождения центра заключается в следующем. Пусть дана плоская металлическая плита с готовым отверстием, центр которого неизвестен. Перед тем как начать разметку, вставляют в отверстие широкий деревянный брусок и на него набивают пластинку из белой жести или из оцинкованного кровельного железа.

Затем на краю отверстия слегка намечают произвольно три точки Л, В и С и из каждой пары этих точек ЛВ и ВС описывают по обе стороны их пересекающиеся между собой дуги-засечки 1—2 и 3—4, рис. 3.46. Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.

Рис. 3.46. Нахождение центра геометрическим способом

Разметка центра циркулем (кронциркулем). Зажав деталь в тиски, растворяют ножки циркуля на величину, немного большую или немного меньшую радиуса размечаемой детали. После этого, приложив к боковой поверхности детали одну ножку циркуля и придерживая ее большим пальцем, другой ножкой циркуля очерчивают дугу. Далее переместив циркуль на 1/4 окружности (на глаз), таким же образом очерчиваю вторую дугу. Затем через каждую четверть окружности очерчивают третью и четвертую дуги. Затем соединить противоположные засечки диагоналями, рис. 3.47я. Центр окружности будет находиться внутри очерченных дуг на пересечении диагоналей.

Рис. 3.47. Разметка центра циркулем (кронциркулем)

Можно разметить центр и способом, показанным на рис. 3.476. Методика разметки аналогична разметке рейсмусом.

Разметка центра колоколом. Приспособление колокол устанавливается на торец цилиндрической детали. Придерживая колокол левой рукой в вертикальном положении, правой рукой наносят удар молотком по кернеру, находящемуся в колоколе, рис. 3.48. Кернер сделает углубление в центре торца.

Рис. 3.48. Разметка центра колоколом

Деление окружности на равные части. При разметке окружностей часто приходится их делить на несколько равных частей — 3, 4, 5, 6, и больше. Ниже приведены примеры деления окружности на равные части геометрическим способом и с помощью таблиц.

Деление окружности на три равные части с построением вписанного треугольника (рис. 3.49).

Рис. 3.49. Деление окружности на три части с построением вписанного треугольника

• 1. В центре размечаемой плоскости с помощью циркуля проводим окружность требуемого радиуса, например R = 26 мм.
• 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
• 3. Опорную ножку циркуля устанавливаем в точку А и при растворе циркуля, равном радиусу проведенной окружности, делаем на окружности две метки-засечки (точки С и D), где длина дуги между ними будет равна одной трети длины окружности.
• 4. Соединив точки прямыми рисками СД СВ и BD, получим вписанный равносторонний треугольник.
• 5. Правильность построения проверяем циркулем, устанавливая раствор циркуля равным одной из сторон треугольника и этим же размером определяя равенство остальных сторон треугольника.

Деление окружности на четыре равные части с построением вписанного квадрата, рис. 3.50.

Рис. 3.50. Деление окружности на четыре части с построением вписанного квадрата (а) и прием разметки квадрата (6)

• 1. В центре размечаемой плоскости циркулем проводим окружность требуемого радиуса, например R= 28 мм.
• 2. Через центр окружности по линейке проводим прямую риску что бы она пересекала окружности в двух точках А и В и разделяла ее на две равные части.
• 3. Опорную ножку циркуля устанавливаем в точку А и, раздвинув циркуль на расстояние несколько большее, чем половина отрезка АВ, проводим дугу в.
• 4. Опорную ножку циркуля переносим в точку В и, не изменяя раствора циркуля, проводим дугу б так, чтобы она пересекла первую выполненную дугу в точках 7 и 2.
• 5. Через точки 7 и 2 проводим риску, которая образует на окружности точки С и D.
• 6. Соединив точки AD, DB, ВС и СА прямыми рисками, получим квадрат, вписанный в окружность.

Деление окружности на пять равных частей (рис. 3.51). На данной окружности проводим два взаимно перпендикулярных диаметра, пересекающие окружность в точках А и В, С и D. Радиус ОА делим пополам и из полученной точки Е описываем дугу радиусом ЕС до пересечения в точке F на радиусе О В. После этого соединяем прямой точки D и F. Откладывая длину прямой DF по окружности, разделим ее на пять равных частей.

Деление окружности на шесть равных частей с построением вписанного шестиугольника, рис. 3.52.

Рис. 3.51. Деление окружности на пять равных частей

Рис. 3.52. Деление окружности на шесть частей с построением вписанного шестиугольника

• 1. В центре разметочной плоскости циркулем проводим окружность требуемого радиуса, например 7? = 27 мм.
• 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
• 3. Из точки А, как из центра, наносим дугу радиусом, равным радиусу проведенной окружности, и получаем точки 7 и 2

Аналогичное построение делаем из точки В, нанося точки 3 и 4. Полученные точки пересечения и концевые точки диаметра будут искомыми точками деления окружности на шесть частей.

4. Соединив точки прямыми рисками А — 1,2 — 4, 4 — В, В — 3, 3 — 1 и 1 — А, получим вписанный шестиугольник.

При разметке граней шестиугольника под размер h зева гаечного ключа (рис. 3.53) радиус описываемой окружности определяется по формуле R = 0,577/г.

Рис. 3.53. Пример разметки шестиугольника под размер зева гаечного ключа

Деление окружности на равные части с помощью таблицы. Эта таблица (табл. 3.5) имеет две графы: «Число делений окружности» и «Число, умножаемое на радиус окружности». Числа первой графы показывают, на сколько равных частей следует делить данную окружность. Во второй графе даны числа, на которые умножают радиус данной окружности. В результате умножения числа, взятого из второй графы, на радиус размечаемой окружности получаем величину хорды, т. е. расстояние по прямой между делениями окружности.

Таблица 3.5. Деление окружности на равные части

[spoiler title=”источники:”]

http://planetcalc.ru/8943/

http://studref.com/560649/tehnika/razmetka_okruzhnostey_tsentrov_otverstiy_delenie_okruzhnosti_ravnye_chasti_postroenie_mnogougolnikov

[/spoiler]

Роль отрезка $%BD$% в этой задаче совершенно непонятна и непонятно также как он проведён. Ниже координатным методом найдено единственное решение $$PQ=frac {28,sqrt {2260-455,sqrt {15}}}{283}$$ из условий того, что обе маленькие окружности касаюся друг друга и соответствующих сторон треугольника, а большая окружность проходит через центры маленьких и через вершины треугольника $%A$% и $%C$%. Ввиду громоздкости ручного счёта все вычисления выполнены в Maple (код и основные результаты на 1-ом скрине). x1 и x2 – первые координаты точек $%P$% и $%Q$%, (x0,y0) – координаты центра большой окружности. На 2-ом скрине – код для чертёжа и сам чертёж, сделанные также в Maple по результатам вычислений:

@Igore Ниже – аналитическое решение в Maple в соответствии с исходной формулировкой. Точный ответ будет $$PQ=frac{7}{sqrt{10}}$$
Задача сводится к решению системы 2-х уравнений с 2-я неизвестными (x1 – первая координата точки $%D$%, y0 – вторая координата точки $%E(x0,y0)$%, очевидно $%x0=frac{7}{2}$%):

Была ли эта статья полезной?

Признак принадлежности четырёх точек одной окружности

 Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

∠ABD=∠ACD

Доказать: точки A, B, C, D лежат на одной окружности

Доказательство:

Обозначим ∠ABD=∠ACD=α.

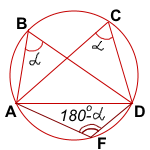
Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

∠ABD+∠AFD=180°.

Отсюда ∠AFD=180°-∠ABD=180°-α.

Рассмотрим четырехугольник ACDF.

∠ACD+∠AFD=α+180°-α=180°.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Что и требовалось доказать.