Ромб – это геометрическая фигура; параллелограмм, имеющие 4 равные стороны.
-
Формула вычисления площади
- По длине стороны и высоте
- По длине стороны и углу
-
По длинам диагоналей
- Примеры задач
Формула вычисления площади
По длине стороны и высоте
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a ⋅ h
По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 ⋅ sin α
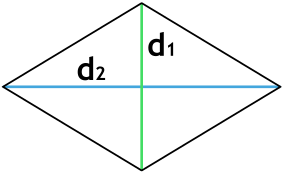
По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
S = 1/2 ⋅ d1 ⋅ d2
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 10 см ⋅ 8 см = 80 см2.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Решение:
Применим вторую формулу, в которой используются известные по условиям задания величины: S = (6 см)2 ⋅ sin 30° = 36 см2 ⋅ 1/2 = 18 см2.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Решение:
Воспользуемся третьей формулой, в которой используются длины диагоналей: S = 1/2 ⋅ 4 см ⋅ 8 см = 16 см2.

{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
Формула площади ромба через сторону и угол
S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту
S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
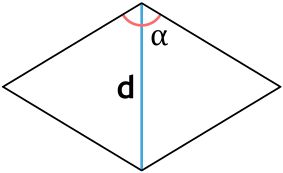
Формула площади ромба через угол и диагональ из угла
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ
S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
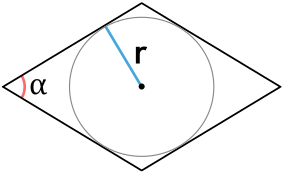
Формула площади ромба через радиус вписанной окружности и угол
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
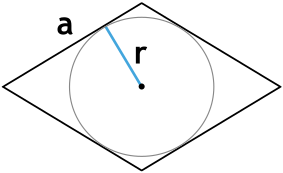
Формула площади ромба через радиус вписанной окружности и сторону
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .
|
Нужно перемножить его диагонали и разделить произведение пополам. Чтобы не зубрить и не путать, можно объяснить как-нибудь этот процесс для себя. Лично я в школе прибегал к такой уловке. Диагонали делят ромб на 4 прямоугольных треугольника. Добавляя еще четыре таких же, мы получим прямоугольник, в который вписан этот ромб. Его площадь равна произведению сторон, которые равны диагоналям ромба. При этом площадь самого прямоугольника в 2 раза больше площади ромба. Поэтому площадь ромба равна половине площади прямоугольника, в который он вписан. Это долго объяснять словами, но картинка говорит сама за себя. автор вопроса выбрал этот ответ лучшим иришенька 6 лет назад Еще со школы помню, что узнать площадь данной фигуры можно так:
К примеру, если диагонали ромба имеют длину 5 и 6 см, то площадь ромба равна 15 см. То есть умножает 5 на 6 и делим на 2. Матвей628 9 лет назад В переводе с латинского слово ромб означает бубен. Это многое объясняет для любителей карточных игр. Просто в древности бубны делали не круглыми, а в виде параллелограммов. Поскольку ромб – параллелограмм, то площадь ромба можно найти несколькими способами. Во-первых, площадь ромба равна половине произведения его диагоналей. Это многие помнят еще со школы. Во-вторых, площадь ромба равна произведению его стороны на высоту. А в-третьих, площадь ромба равна произведению квадрата его стороны на синус прилегающего угла. Alexgroovy 6 лет назад Рассчитать площадь ромба можно различными способами. Наиболее простой формулой, по моему мнению, является произведение длины перпендикуляра, проведенного из угла к противоположной стороне, и длины этой стороны. Для наглядности размещаю схематичный вид поиска площади ромба. Согласно другому способу, зная расстояние двух диагоналей фигуры, легко произвести искомый расчет. Bokatashka 8 лет назад Ромб – это параллелограмм, у которого все стороны равны. Квадрат тоже является ромбом, это частный случай. для расчета площади ромба существует формула: S= 1/2 d1*d2, где d1, d2 – диагонали ромба. То есть площадь ромба равна половине произведения его диагоналей. Так как ромб – это параллелограмм, то площадь также равна произвению его стороны на высоту. Samborskaya 9 лет назад Площадь ромба можно вычислить по нескольким формулам, важно знать хоть какие-нибудь величины, характеризующие его. Если известны его диагонали, то площадь – это произведение диагоналей, разделенные на два. Если знаете его сторону и высоту, то их нужно перемножить, чтобы узнать площадь. Galina7v7 7 лет назад Площадь ромба S можно найти несколькими способами:1)S=a*a*sinA=a^2*sinA,где а -сторона ромба,А-угол между сторонами.2)S=а*h,где а-сторона ромба,h-высота,опущенная на сторону из вершины.3)S=d1*d2,где d1,d2-диагонали ромба.Делить на 2 не надо,просто перемножить диагонали! Для того что бы найти площадь ромба, необходимо знать, что площадь ромба равна половине произведений его диагоналей. Это дети учат в восьмом классе. Так же, нужно знать, что ромб является параллелограммом, его площадь так же равна произведению его стороны на высоту. Это сделать легко. Нужно умножить одну диагональ на другую. Полученное произведение дальше делится пополам. Это и будет искомая площадь такой фигуры,как ромб. Сложность в том,что в задачах как правило,сначала нужно узнать,чему же равны диагонали ромба. Master key 111 6 лет назад Площадь ромба определяется пересечением двух прямых по середине данной геометрической фигуры, делается это достаточно просто, проведя две линии выявляется непосредственно площадь ромба, которая напрямую зависит от сторон того же ромба. МарияСС 7 лет назад Возможны три варианта нахождения площади ромба, в зависимости от исходных данных: 1) даны основание (а) и высота (h). S=a*h. 2) даны сторона (a) и угол между ними (y). S=a*a*sin(y). 3) даны размеры диагоналей (d1 и d2). S=d1*d2/2. alexm12 10 лет назад Так же как и параллелограмма, ромб же частный случай параллелограмма Знаете ответ? |
Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!
Тест на тему “Площадь ромба”
Загрузить PDF
Загрузить PDF
Ромб — это четырехугольный параллелограмм с четырьмя равными сторонами, площадь которого можно вычислить по четырем разным формулам. Если хотите узнать, как это сделать, следуйте инструкциям:
-
1
Определите длину каждой диагонали. Диагонали ромба — это линии, соединяющие противоположные углы в центре фигуры. Диагонали ромба перпендикулярны и после пересечения образуют четыре правильных треугольника.
- Предположим, диагонали составляют шесть и восемь сантиметров.
-
2
Перемножьте длину диагоналей. Запишите длину и умножьте одно число на другое. В нашем случае это составит 6 см x 8 см = 48 см2. Не забывайте указывать квадратные единицы, так как вы работаете с квадратной площадью.
-
3
Разделите результат на два. Как мы помним, 6 см x 8 см = 48 см2, остается только разделить на два. 48 см2/2 = 24 см2. Площадь нашего ромба составляет 24 см2.
Реклама
-
1
Определите основание и высоту. Вы можете также подумать об этом как об умножении высоты ромба на длину стороны. Скажем, высота ромба составляет десять сантиметров, а основание — семь сантиметров.
-
2
Перемножьте основание и высоту. Зная основание и высоту ромба, вам остается только умножить одно на другое. 10 см x 7 см = 70 см2. Площадь нашего ромба составляет 70 см2.
Реклама
-
1
Возведите длину одной стороны в квадрат. У ромба имеется четыре равные стороны, так что не важно, какую именно вы выберете. Предположим, сторона равна двум сантиметрам. 2 см x 2 см = 4 см2.
-
2
Умножьте ее на синус одного из углов, неважно какого. Предположим, один из углов составляет 33 градуса. Умножьте синус (33) на 4 см2 — и вы получите площадь ромба. (2 см)2 x синус (33) = 4 см2 x 1 = 4 см2. Площадь нашего ромба составляет 4 см2.
Реклама
Об этой статье
Эту страницу просматривали 43 470 раз.