Что такое движение тела брошенного под углом к горизонту
Определение
Движением тела под углом к горизонту в физике называют сложное криволинейное перемещение, которое состоит из двух независимых движений, включая равномерное прямолинейное движение в горизонтальном направлении и свободное падение по вертикали.
В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.
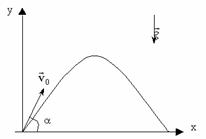
На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Направление вектора скорости тела, которое подбросили под определенным углом к горизонту, будет совпадать с касательной к траектории его перемещения.
- Начальная скорость отличается от направления горизонтальной линии, а обе ее проекции не равны нулю.
- Проекция скорости в начале движения на ось ОХ составляет (V_{ox}=V_{0}cos alpha).
- Проекция начальной скорости на ось ОУ равна (V_{oy}=V_{0}sin alpha).
- Проекция мгновенной скорости на ось ОХ следующая: (V_{x}=V_{0}cos alpha).
- Проекция мгновенной скорости на ось ОУ обладает нулевым значением и рассчитывается следующим образом: (V_{x}=V_{0}sin alpha-gt).
- Ускорение свободного падения на ось ОХ обладает нулевой проекцией, или (g_{x}=0).
- Проекция ускорения свободного падения на ось ОУ равна (–g), или (g_{y}=-g).
К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:
(V=sqrt{V^{2}_{x}+V^{2}_{y}})
Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.
Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.
Определение
Горизонтальным смещением тела называют смещение данного объекта, относительно оси ОХ.
Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:
(x=x_{0}+V_{0x}t+frac{gxt^{2}}{2})
Зная следующие условия:
- (x_{0}=0);
- проекция ускорения свободного падения, относительно оси ОХ, также имеет нулевое значение;
- проекция начальной скорости на ось ОХ составляет (V_{0}cos alpha).
Записанная формула приобретает следующий вид:
(x=V_{0}cos alpha t)
Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.
Вывод формулы, как найти угол и дальность полета
Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:
- равномерное горизонтальное движение;
- равноускоренное перемещение в вертикальном направлении с ускорением свободного падения.
Скорость тела будет рассчитываться таким образом:
(v_{0x}=v_{x}=v_{0} cos alpha =const)
(v_{0y}=v_{0}sin alpha)
(v_{y}=v_{0}sin alpha-gt)
Уравнение координаты записывают в следующем виде:
(x=v_{0}cos alpha times t)
(y=v_{0}sin alpha times t-frac{gt^{2}}{2})
В любое время значения скорости тела будут равны:
(v=sqrt{v_{x}^{2}+v_{y}^{2}})
Определить угол между вектором скорости и осью ОХ можно таким образом:
(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })
Время подъема на максимальную высоту составляет:
(t=frac{v_{0}sin alpha }{g})
Максимальная высота подъема будет рассчитана следующим образом:
(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})
Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:
(t=frac{2v_{0}sin alpha }{g})
Максимальная дальность полета составит:
(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})
Примеры решения задач
В примерах, описывающих движение тела, на которое действует сила тяжести, следует учитывать, что а=g=9,8 м/с2.
Задача 1
Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.
Решение
Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:
(V_{0}sin alpha =gt)
Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:
(h=frac{V_{0}sin ^{2}alpha }{2g}=frac{(gt)^{2}}{2g}=frac{gt^{2}}{2}=frac{10times 1}{2}=5)
Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.
Задача 2
Из орудия выпустили снаряд, начальная скорость которого составляет 490 м/с, под углом 30 градусов к горизонту. Нужно рассчитать, какова высота, дальность и время полета снаряда без учета его вращения и сопротивления воздуха.
Решение
Систему координат и движение тела можно представить схематично:
Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:
(V_{0x}=V_{0} cos alpha) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.
(V_{0y}=V_{0}sin alpha) будет меняться, согласно формуле равнопеременного движения (V_{y}=V_{0}sin alpha-gt).
В максимальной точке, на которую поднимется снаряд:
(V_{y}=V_{0}sin alpha-gt_{1}=0)
Из этого равенства следует:
(t=frac{V_{0sin alpha }}{g})
Полное время полета тела будет рассчитано по формуле:
(t=2t_{1}=frac{2V_{0}sin alpha }{g}=50)
Высота, на которую поднимется снаряд, определяется с помощью уравнения равнозамедленного перемещения тела:
(h=V_{0y}t_{1}-frac{gt_{1}^{2}}{2}=frac{V_{0}^{2}sin ^{2}alpha }{2g}=3060)
Дальность полета снаряда будет рассчитана таким образом:
(S=V_{0x}t=frac{V_{0}^{2}sin 2alpha }{g}=21000)
Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.
В статье подробно, начиная с основ и базовых определений, рассказано о движении тела брошенного под углом к горизонту. Здесь вы найдете формулы параметров движения: общее время, дальность полета, максимальная высота. Также в конце приложены примеры задач с решениями.
Определение. Баллистическое движение — это движение некоторого тела в поле тяжести Земли при условии, что тело имеет вертикальную и горизонтальную проекции скорости.
Вначале вспомним основные формулы для равноускоренного движения.
Изменение скорости с течением времени задаётся соотношением
vₓ = v₀ₓ + aₓt,
где vₓ — конечная проекция скорости, v₀ₓ — начальная проекция скорости, aₓ — проекция ускорения тела.
Изменение координаты x во времени можно найти, используя следующее соотношение:
x = x₀ + v₀ₓt + aₓt² / 2,
где x — конечная координата тела, x₀ — начальная координата, v₀ₓ — начальная проекция скорости тела вдоль оси OX, aₓ — проекция ускорения тела.

Замечание 1. Перемещением тела за время t называется величина Sₓ = x – x₀.
Замечание 2. Так как эти выражения справедливы для проекций, то их можно записать и в векторном виде.
Баллистическое движение — это случай равноускоренного движения (с постоянным ускорением свободного падения g). Любое тело, брошенное под углом α к горизонту, имеет некоторую вертикальную и горизонтальную проекции скорости (рис. 1).
Далее движение необходимо разбить на два участка:
- Горизонтальное
- Вертикальное
По горизонтали тело движется с одинаковой скоростью (обычно пренебрегаем силами различного трения):
v₁ = v₀cos(α)
А по вертикали это обычное движение тела, брошенного вертикально вверх с начальной скоростью:
v₂ = v₀sin(α)
Общее время движения
Разобьём траекторию на два участка. Первый — участок, на котором тело продолжает подниматься, а второй — участок, где тело спускается. Обозначим t₁ время подъёма тела (от нуля до максимальной высоты подъема), t₂ — время спуска тела.
Из уравнения движения:
v₀sin(α) – gt₁ = 0
(так как конечная проекция скорости в верхней точке траектории равна нулю),
t₁ = v₀sin(α) / g.
Найдём время спуска:
–gt₂ = –v₀sin(α),
(т. к. конечная скорость тела будет такая же, как и начальная),
t₂ = v₀sin(α) / g.
Общее время движения:
t = t₁ + t₂ = 2v₀sin(α) / g.
Замечание.Время спуска и время подъёма тела одинаковые. Это связано с тем, что движение симметрично.
Дальность полета
Так как по горизонтали (вдоль оси ОХ) движение тела равномерное, то, зная общее время движения, найдём дальность полета L:
L = tv₁ = (2v₀sin(α) / g) · v₀cos(α) = 2v₀²sin(α)cos(α) / g.
Замечание. Используя формулу из тригонометрии
2sin(α)cos(α) = sin(2α),
получим:
L = 2v₀²sin(2α) / g.
Следовательно, максимальная дальность полета тела будет при броске под углом 45° к горизонту (так как sin(90°) = 1).
Максимальная высота подъёма тела
Рассмотрим движение тела в проекции на ось OY:
H = v₀sin(α)t₁ – gt₁² / 2.
После подставления времени подъёма получим
H = v₀²sin²(α) / (2g).
Давайте теперь решим некоторые задачи.
Задачи
Задача 1. Пуля, летящая горизонтально со скоростью v = 500 м/с, пробивает первый листок бумаги. Найти, на каком расстоянии S находится второй листок бумаги, если известно, что его пуля пробила на h = 20 см ниже, чем первый.
Решение. Найдём, за какое время пуля прошла расстояние между листами. Нам известно, что за это же время она опустилась на высоту h = 20 см. Тогда:
h = gt² / 2,
t = √(2h/g).
Теперь, зная время движения пули между листами, найдём расстояние, которое прошла пуля за это время:
S = tv = v · √(2h/g) = 100 м.
Ответ: S = 100 м.
Задача 2. Школьник может бросить мяч в спортивном зале с максимальной скоростью v = 25 м/с. Пренебрегая силами сопротивления воздуха, найти максимальную дальность полета мяча в спортивном зале, если высота зала равна h = 4 м. Считать, что мяч не ударяется о потолок.
Решение. Пусть мальчик бросил мяч под некоторым углом α к горизонту. Тогда дальность полета мяча равна:
L = 2v₀²sin(α)cos(α) / g.
Как обсуждалось выше, тело имеет максимальную дальность полета, если его бросить под углом α = 45° к горизонту. Но в данной задаче возможно, что при таком угле мяч ударится о потолок. Проверим, какова максимальная высота подъёма мяча при условии, что угол равен α = 45°.
H = v₀²sin²(α) / (2g) = 16 м.
Следовательно, угол, под которым мальчик бросит мяч, будет значительно меньше. Найдём максимальный угол, при котором мяч не столкнется с потолком. Этот угол будет соответствовать предельному случаю, когда мяч побывает на высоте h = 4 м.
h = v₀²sin²(α) / (2g) => sin²(α) = 2gh / v₀².
Из основного тригонометрического тождества
sin²(α) + cos²(α) = 1
найдём cos²(α):
cos²(α) = 1 – 2gh / v₀².
Подставив все выражения в дальность полета L, получим:
L = 2√(2gh(v₀² – 2gh)) / g = 42 м.
Ответ: L = 42 м.
Замечание. Если в задаче не приведены числовые значения (задача в общем виде), то необходимо записать 2 ответа. Первый ответ при условии высокого потолка, при h > H —
L = 2v₀²sin(α)cos(α) / g, α = 45°.
И при h < H получаем ответ
L = 2√(2gh(v₀² – 2gh)) / g.
Список литературы
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
Автор: Роман Федоренко
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
![]()
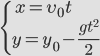
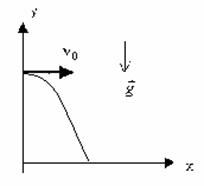
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
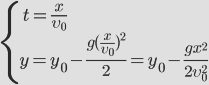
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
![]()
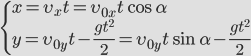
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
![]() .
.
Мы получили квадратичную зависимость между координатами. Значит траектория – парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Время полета:

![]()

Зная время полета, найдем максимальное расстояние, которое пролетит тело:
![]()
Дальность полета:
![]()
Из этой формулы следует, что:
– максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
– на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
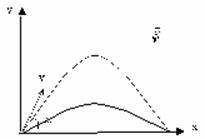
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 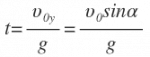
Время подъема:
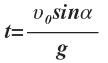
Тогда: ![]()
Максимальная высота:
![]()
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна ![]()
Угол, под которым направлен вектор скорости в любой момент времени:
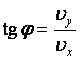
ФГБОУ
ВПО
«Воронежский
государственный технический университет»

Кафедра
самолетостроения
Расчет дальности полета самолета методические указания
к
выполнению курсовой
и
дипломной работ по дисциплине
«Аэродинамика
и динамика полёта»
для
студентов специальности 160100.65 «Самолето-
и вертолетостроение»
очной и очно-заочной форм обучения
Воронеж 2012
Составитель
канд. техн. наук В.А. Сатин
УДК 629.7.015
Методические
указания
к
выполнению курсовой и дипломной работ
по дисциплине «Аэромеханика самолета»
для студентов специальности 160100.65
«Самолето- и вертолетостроение» очной
и очно-заочной форм обучения/ФГБОУ ВПО
«Воронежский государственный технический
университет»; сост. В.А. Сатин. Воронеж,
2012. 22 с.
Методические
указания содержат описания расчетов
дальности полета самолетов с ТРД и ТВД,
приводится методика расчета дальности
полета с учетом отказа двигателя и
влиянием ветра, а также указаны особенности
расчетов дальности полета сверхзвуковых
самолетов.
Предназначены для
студентов 2-5 курсов.
Ил. 6.
Рецензент:
канд. техн. наук, доцент А.П. Будник
Ответственный
за выпуск зав. кафедрой самолетостроения
д-р техн. наук, проф. В.И. Корольков.
Издается
по решению редакционно-издательского
совета Воронежского государственного
технического университета.
© ФГБОУ
ВПО «Воронежский государственный
технический университет», 2012
ВВЕДЕНИЕ
Дальность полета
самолета приближенно можно представить
как сумму дальности полета на участке
разгона и подъема самолета (Lп),
на крейсерском участке полета (Lк)
и на участке снижения (Lсн)
![]()
.
(1)
Ниже будут
рассмотрены методы расчета дальности
полета на каждом из участков, при этом
вопросы устойчивости и управляемости
при движении самолета рассматриваться
не будут. Для расчетов необходимо иметь
аэродинамические характеристики
самолетов и характеристики двигателей,
а также барограмму подъёма самолета.
1. Дальность полета самолета на участке набора высоты
Расстояние по
горизонтали, которое проходит самолет
при наборе высоты определяется
зависимостью
![]()
,
(2)
где t
– время набора заданной высоты; Vнаб
– скорость набора высоты; θ – угол
наклона траектории.
Будем рассматривать
установившийся подъём – равномерное
и прямолинейное движение самолета вверх
по наклонной траектории. В этом случае
имеем
![]()
.
(3)
Скорость набора
высоты определяется выражением
![]()
.
(4)
где G
– вес самолета;
![]()
–
коэффициент подъёмной силы самолета
при наборе высоты;
![]()
–
плотность воздуха.
Расчета дальности
полета при наборе высоты проводится в
следующей последовательности:
-
Задается угол
наклона траектории θ. -
Определяется
скорость набора высоты по формуле (4). -
Определив по
барограмме подъёма время достижения
заданной высоты крейсерского полета
t,
по выражению (3) определяется дальность
полета на участке набора высоты.
Если угол наклона
траектории не задан, то его можно найти
по формуле
![]()
,
где (Рр
– Рп)
разность между располагаемой и потребной
тягами, которая определяется по диаграмме
тяг.
Более точно угол
наклона определится зависимостью

,
где К – качество
самолета;
![]()
–
тяговооруженность, определяемая как
![]()
,
здесь
![]()
–
суммарная тяга двигателей.
Для самолетов с
ТВД угол наклона траектории можно
определить как
![]()
,
где (Nр
– Nп)
разность между располагаемой мощностью
двигателей и потребной мощностью,
определяется по диаграмме мощностей.
Если набор высоты
проходит в установившемся режиме (Vнаб
= const),
но по криволинейной траектории, то
дальность определяется зависимостью
![]()
.
(5)
В этом случае
необходимо знать, как изменяется угол
наклона траектории в зависимости от
времени полета. Если известно аналитическое
выражение для закона изменения θ, то
после подстановки его в интеграл (5)
определяется дальность полета. Интеграл
(5) можно решать графически.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти дальность и высоту полета тела брошенного горизонтально?
Время полета, дальность полета тела брошенного горизонтально y=h0−gtpol22=0→h0=gtpol22→tpol=√2h0g(10). Дальность полета (s) — это расстояние, которое тело преодолело по горизонтали (по оси X). Его найдем, подставив время полета в первое уравнение системы (8):
Как можно определить высоту подъема пули?
Максимальная высота подъёма тела, брошенного под углом к горизонту, вычисляется по формуле h=(v⋅sinα)22g h = ( v ⋅ s i n α ) 2 2 g где v (м/c) – начальная скорость тела, α – угол, под которым тело брошено к горизонту, g – ускорение свободного падения (считать, что g=10 м/ 2).
Как найти путь тела брошенного горизонтально?
v=√v2x+v2y=√v20+g2t2(6). Уравнение для перемещения тела, брошенного горизонтально, запишем как: ¯s(t)=¯s0+¯v0t+¯gt22(7), где ¯s0 — смещение тела в начальный момент времени.
Как рассматривают движение тел брошенных горизонтально или под углом к горизонту?
Движение тела, брошенного горизонтально или под углом к горизонту. Это движение в плоскости, поэтому для описания движения необходимо 2 координаты. Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Как определить есть ли начальная скорость?
Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- Vi = (d / t) — [(a * t) / 2]
- В эту формулу входят следующие величины: Vi — начальная скорость d — пройденное расстояние a — ускорение t — время
Как зависит дальность полета тела от высоты h?
Ответ: при увеличении высоты увеличивается дальность полета.
Как найти высоту в кинематике?
В данном случае можем воспользоватся формулой H = (g*t^2) / 2. Где H — искомая высота g-ускорение свободного падения равное 9.8 м/c^2 t-время падения.
Что такое максимальная высота?
Максимальная высота полета баллистической ракеты — Максимальная высота означает расстояние, измеряемое по нормали к земному эллипсоиду от его поверхности до высшей точки траектории полета ракеты…
Как найти путь при движении по окружности?
Δl = R Δφ.
Что такое уравнение траектории?
Так как ускорение свободного падения g и начальная скорость тела u0 — постоянные величины, то координата y пропорциональна квадрату x, т. е. траектория движения представляет собой параболу, вершина которой находится в начальной точке движения.
Как направлен вектор мгновенной скорости по отношению к траектории движения?
Вектор мгновенной скорости направлен по касательной к траектории движения (рис. 1.3).
Как найти начальную скорость тела?
Если известны пройденное расстояние, время и ускорение, для определения начальной скорости можно использовать следующее соотношение:
- Vi = (d / t) — [(a * t) / 2]
- В эту формулу входят следующие величины: Vi — начальная скорость d — пройденное расстояние a — ускорение t — время
Как найти Как найти скорость?
Чтобы найти скорость, нужно расстояние разделить на время движения. Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
Как зависит дальность полета от начальной скорости?
Ответ: дальность полета тела, брошенного в горизонтальном направлении прямо пропорциональна начальной скорости движения.
Почему траектория движения тела брошенного горизонтально искривляется?
1. Почему траектория движения тела, брошенного горизонтально, искривляется? Скорость тела, брошенного горизонтально, по оси x не изменяется, а по оси y увеличивается за счёт действия на тело силы g (ускорение свободного падения).
Как найти высоту в физике все формулы?
В данном случае можем воспользоватся формулой H = (g*t^2) / 2. Где H — искомая высота g-ускорение свободного падения равное 9.8 м/c^2 t-время падения. Тогда скорость сможем рассчитать по формуле V=g*t.
Как найти высоту с помощью давления?
При расчете давления по формуле p = gρh надо плотность ρ выражать в килограммах на кубический метр (кг/м3), а высоту столба жидкости h — в метрах (м), g = 9,8 Н/кг, тогда давление будет выражено в паскалях (Па).
