Параллелепипед – это частный случай призмы, в основании которой лежит прямоугольник с длиной a и шириной b. Двигаясь по вертикальной или наклонной оси на определенную высоту c, данный прямоугольник создает объемное тело, именуемое параллелепипедом.
Параллелепипед по определению может быть наклонным или прямым, то есть угол между высотой и прямоугольником в основании варьируется от 0 до 90 градусов. Прямой параллелепипед имеет в качестве граней исключительно прямоугольники, и даже иногда квадрат (в основании), поэтому решение задач с его участием значительно облегчено. В случае с наклонным параллелепипедом в формулах необходимо учитывать, что боковой гранью является параллелограмм, строение которого зависит также от угла его наклона.
Помимо трех вышеуказанных параметров параллелепипеда – длины, ширины высоты, являющихся его ребрами, в данном теле можно также провести еще несколько отрезков, соединяющих его вершины. Как и в геометрических фигурах на плоскости, линии, проходящие внутри основного каркаса через вершины, называются диагоналями. Диагонали боковых граней прямоугольного параллелепипеда идентичны диагоналям прямоугольников, которыми представлены грани – их, соответственно, можно вычислить, используя подходящий онлайн калькулятор для прямоугольников.
Другое дело – диагональ, проходящая не по внешней поверхности прямоугольного параллелепипеда, а сквозь него, соединяя противоположные вершины верхнего и нижнего оснований. При этом, какая именно пара противоположных вершин соединена, не имеет значения для расчетов, так как если рассмотреть сечения, можно увидеть, что обе диагонали параллелепипеда идентичны и найти их можно одним и тем же способом.
Итак, для того чтобы вывести формулу диагонали через длину, ширину и высоту, необходимо заключить диагональ в плоскую геометрическую фигуру, свойства которой можно будет использовать. Для этого в любом основании – верхнем или нижнем, проводится диагональ, которая образует с диагональю параллелепипеда и боковым ребром (высотой) прямоугольный треугольник. Применив одну лишь теорему Пифагора, можно найти диагональ основания через ширину и длину,а затем диагональ прямоугольного параллелепипеда, добавив в расчеты высоту.
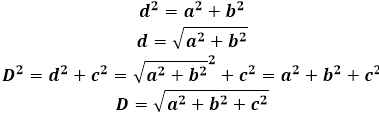
Используя последнюю и предпоследнюю формулу, можно также успешно найти длину, ширину или высоту прямоугольного параллелепипеда, имея в заданных условиях три параметра из четырех, включая диагональ параллелепипеда.
Например: 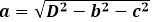
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Прямая призма, основанием которой является прямоугольник, называется прямоугольным параллелепипедом.
Длины трёх рёбер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
Например, три измерения — это длины трёх рёбер
DA,DC,DD1
.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
,
где (a, b, c) — измерения прямоугольного параллелепипеда, т. е. его длина, ширина и высота.
На рисунке:
DB12=DA2+DC2+DD12
.
Обрати внимание!
У прямоугольного параллелепипеда все диагонали равны:
Пример:
формула диагоналей куба.
Так как у куба все измерения равны, обозначаем их за (a), тогда
Упрощаем и получаем формулу диагонали куба:
|
Как найти длину диагонали прямоугольного параллелепипеда ? По какой формуле найти диагональ параллелепипеда ?
Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий его противоположные вершины . Итак, у нас есть прямоугольный параллелепипед с диагональю d и со сторонами a, b, c . Одно из свойств параллелепипеда гласит, что квадрат длины диагонали d равен сумме квадратов трёх его измерений a, b, c. Отсюда вывод, что длина диагонали может быть легко рассчитана по следующей формуле :
Также :Как найти высоту параллелепипеда?модератор выбрал этот ответ лучшим
Nonsense 7 лет назад Прямоугольным параллелепипедом (ПП) является ни что иное, как призма, основанием у которой прямоугольник. У ПП все диагонали равны, значит любая его диагональ рассчитывается по формуле:
где
Можно дать и другое определение, рассматривая декартову прямоугольную систему координат: Диагональ ПП это радиус-вектор любой точки пространства, заданной координатами x, y и z в декартовой системе координат. Этот радиус вектор к точке проводится из начала координат. А координатами точки будут проекции радиус-вектора (диагонали ПП) на координатные оси. Проекции совпадают с вершинами данного параллелепипеда.
Zolotynka 8 лет назад Если у прямоугольного параллелепипеда известны длина, высота и ширина (a,b,c) то формула для расчета диагонали будет выглядеть таким образом:
Обычно учителя не предлагают своим ученикам “голую” формулу, а прилагают усилия, чтобы те могли самостоятельно ее вывести, задавая наводящие вопросы:
Обычно после ответа на поставленные вопросы, ученики без труда самостоятельно выводят данную формулу.
Лолочка611 8 лет назад Прямоугольный параллелепипед это один из так званных многогранников, который состоит из 6 граней, каждая из которых является прямоугольником. А диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Если длину, ширину и высоту прямоугольного параллелепипеда принять за a, b, c соответственно, то формула его диагонали ( D ) будет выглядеть следующим образом: D^2=a^2+b^2+c^2.
дольфаника 8 лет назад Нашлась в интернете неплохая схема-таблица с полным перечислением всего, что есть в параллепипеде. Есть формула, чтобы найти диагональ, которая обозначается d. Есть изображение грани, вершины и других важных для параллепипеде вещей.
Багира999 8 лет назад Прямоугольный параллелепипед – это разновидность многогранника, состоящая из 6 граней, в основании которого — прямоугольник. Диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Формула нахождения длины диагонали – квадрат диагонали равен сумме квадратов трех измерений параллелограмма.
Koluchiy 8 лет назад Диагонали прямоугольного параллелепипеда равны. Также как и диагонали его противоположных граней. Длину диагонали можно вычислить, зная длину рёбер параллелограмма, исходящих из одной вершины. Эта длина равна корню квадратному из суммы квадратов длин его рёбер.
ДРЕССИРОВЩИК 9 лет назад Квадрат диагонали, квадратного параллилепипеда (смотрите свойства квадратного параллепипеда) равна сумме квадратов трёх его разных сторон (ширине, высоте, толщине), а соответственно диагонали квадратного параллепипеда равна корню из этой суммы.
haleron 8 лет назад Насколько мне известно еще со школьной программы, класс 9 если не ошибаюсь, и если не изменяет память , то диагональ прямоугольного параллелепипеда ровна корню квадратному суммы квадратов его всех трех сторон. [пользователь заблокирован] 8 лет назад квадрат диагонали равен, сумме квадратов ширины , высоты и длинны , исходя с этой формулы получаем ответ , диагональ равно корню квадратному с суммы его трех разных измерений , буквами они позначаюnсz abc
Космос111 7 лет назад Вспоминаю школьную программу по геометрии, можно сказать так: диагональ параллелепипеда равняется корню квадратному полученному из суммы его всех трех сторон (обозначаются они маленькими буквами a, b, c). Николай Л 10 лет назад Длина диагонали прямоугольного параллепипеда равна корню квадратному из суммы квадратов его сторон. Знаете ответ? |
Принцип нахождения диагонали прямоугольного параллелепипеда совпадает с принципом вычисления диагонали куба. Необходимо точно также соединить противоположные вершины нижнего основания, чтобы получить с ребром параллелепипеда и его диагональю прямоугольный треугольник. Диагональ основания из теоремы Пифагора будет равна сумме квадратов ребер в основании:

Зная диагональ основания, подставляем ее в теорему Пифагора в нужном нам треугольнике.
d2=dосн.2+a2
d2=b2+c2+a2
Как найти диагональ прямоугольного параллелепипеда
Прямоугольный параллелепипед – это разновидность многогранника, состоящая из 6 граней, каждая из которых является прямоугольником. В свою очередь, диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Его длину можно найти двумя методами.
Вам понадобится
- Знание длины всех сторон параллелограмма.
Инструкция
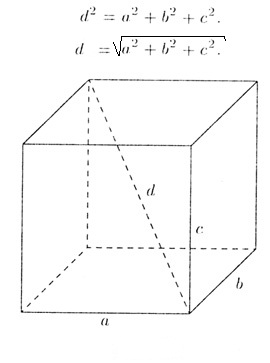
Метод 1. Дан прямоугольный параллелепипед со сторонами a, b, c и диагональю d. Согласно одному из свойств параллелограмма, квадрат диагонали равен сумме квадратов трех его сторон. Отсюда следует, что сама длина диагонали может быть рассчитана с помощью извлечения квадрата из данной суммы (рис.1).
Метод 2. Допустим, что прямоугольный параллелепипед является кубом. Куб – это такой прямоугольный параллелепипед, у которого каждая грань представлена квадратом. Следовательно, все его стороны равны. Тогда формула для расчеты длины его диагонали будет выражена так:
d = a*√3
Источники:
- формула диагонали прямоугольника
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.










