Главная › ЕГЭ. Стереометрия
В правильной четырехугольной пирамиде найти диагональ основания
Автор: Ирина Гайкова
Комментариев нет
432
Telegram
VK
OK
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SD = 10, SO = 6. Найдите длину отрезка AС.
Интересная статья? Поделитесь ею пожалуйста с другими:

Хотите обучаться математике индивидуально?
Запишитесь на консультацию.
Мы храним ваши данные в тайне
Похожие записи:
-
Диагональ куба равна √12. Найдите его объем.
-
В сосуд, имеющий форму правильной треугольной призмы, налили воду
-
Найдите объем прямой треугольной призмы.
Оставьте свой комментарий:
- на Блоге
- в Вконтакте
- в Фейсбук









 Еще смайлы
Еще смайлы
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий
Имя *
Email *
Вебсайт
Получать новые комментарии по электронной почте. Вы можете подписаться без комментирования.
Нажимая на кнопку “Отправить комментарий”, я соглашаюсь с политикой обработки персональных данных
как найти диагональ основания четырехугольной пирамиды?
Ангелина Вернер
Ученик
(110),
на голосовании
10 лет назад
Дополнен 10 лет назад
Правильная четырехугольная пирамида SABCD ,
О-центр основания, S-вершина SO=4,SC=5 Найти длину отрезка AC
как я поняла это диагональ основания
Голосование за лучший ответ

Диагональным сечением данной пирамиды является равнобокая трапеция АА1С1С.
Так как A1С1 и АС — диагонали квадратов, A1B1C1D1 и ABCD, то

Проведем A1K⊥AC и C1H⊥AC. Тогда А1С1HK — прямоугольник и А1С1 = КН. Так что, прямоугольные треугольники АА1К и СС1Н равны по гипотенузе и катету.
Тогда,
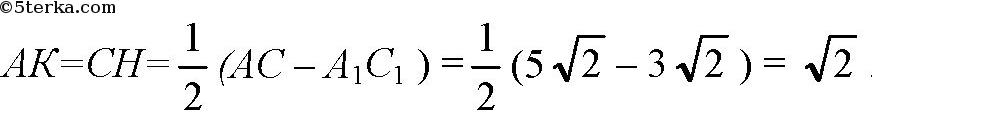
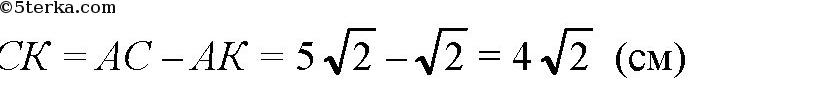
и по теореме Пифагора в ΔА1СК:
Тогда

Ответ: 6 см.
Источник:

Решебник
по
геометрии
за 11 класс (А.В. Погорелов, 2001 год),
задача №72
к главе «§ 20. Многогранники».
Все задачи
← 71. Стороны оснований правильной усеченной треугольной пирамиды 4дм и 1дм. Боковое ребро 2 дм. Найдите высоту пирамиды.
73. Стороны оснований усеченной правильной треугольной пирамиды 2 см и 6 см. Боковая грань образует с большим основанием угол 60°. Найдите высоту. →
Комментарии
Так как основания верхней и нижней являются квадраты то диагональ которую мы хотим найти являеться диагональю прямоугольной трапеций A1C1AF, найдем диагональ оснований
d1=V3^2+3^2=3V2см
d2=V5^2+5^2=5V2см
теперь FC=(5V2-3V2)/2=2V2/2=V2 см
значит катет AF=5V2-V2=4V2см
значит по теорее пифагора найдем диагональ самой пирамиды усеченной
d=V(4V2)^2+2^2=V32+4=V36= 6 см
Ответ 6 см
Приложения:
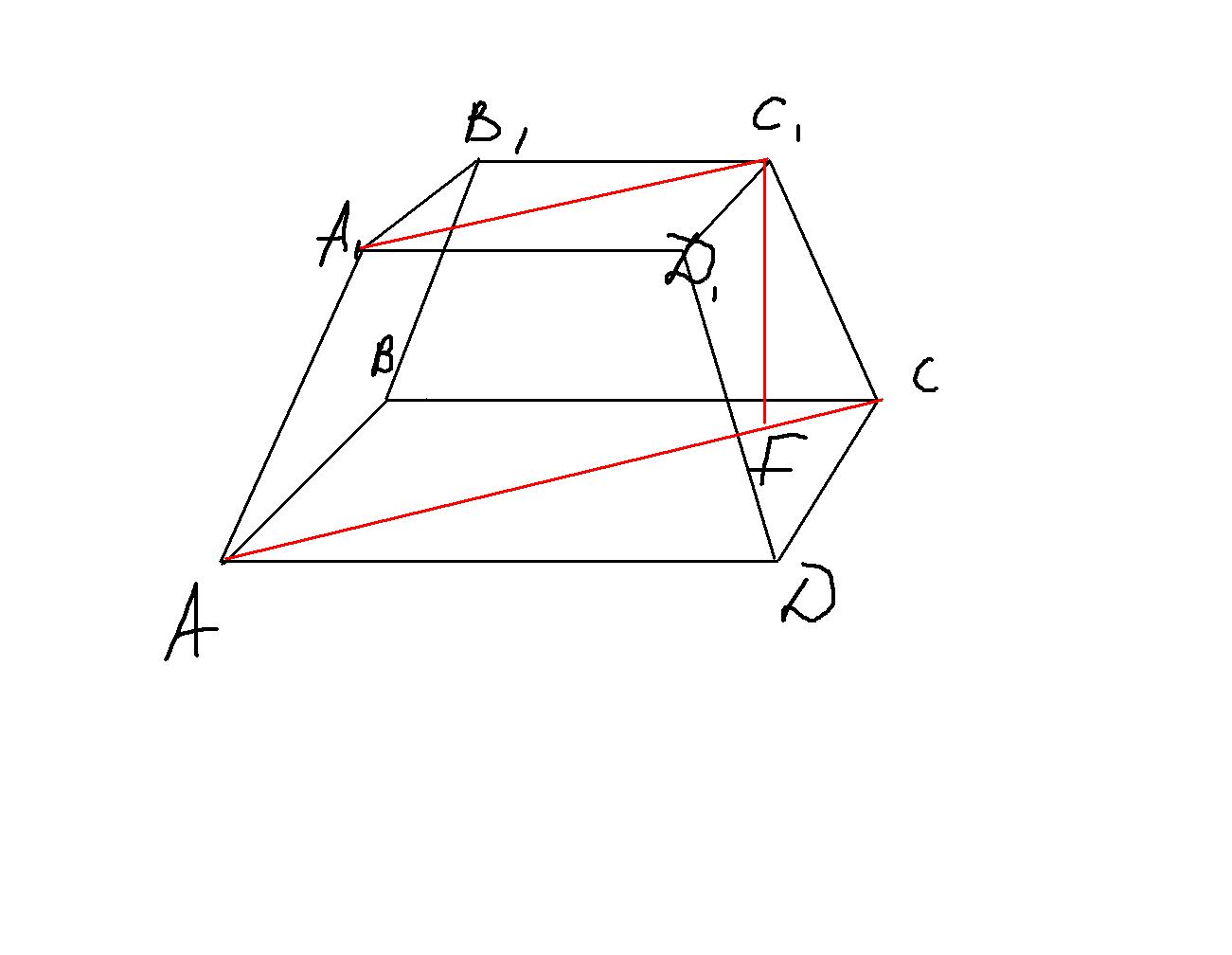
диагональ большего основания=5√2(5*5+5*5=50)
диагональ меньшего основания =3√2(3*3+3*3=18)
5√2-3√2=2√2 разница диагоналей оснований
Из прямоугольного треугольника с катетами 2 и 4√2 (5√2-√2=4√2) найдем диагональ
(4√2)²+2²=32+4=36
диагональ =6
Приложения:

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. В задачах вместо символа “квадратный корень” применяется функция sqrt(), в которой sqrt – символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак “√”.
Задача.
Диагональ основания правильной четырехугольной пирамиды равна 4 см, а боковая грань образует с основанием угол 60 градусов. найдите объем пирамиды.
Решение.
Объем пирамиды найдем по формуле:
V=1/3 Sh
Зная диагональ основания пирамиды, найдем сторону основания.
d2 = a2 + a2
42 = 2a2
16 = 2a2
a= √8 = 2√2
Соответственно, площадь основания
S = 8 см2 .
Проведем через вершину правильной четырехугольной пирамиды вертикальное сечение. Поскольку боковые грани пирамиды наклонены к основанию под углом 60 градусов, то сечение образует равносторонний треугольник.
Основание равностороннего треугольника равно 2√2. Откуда высота будет равна
h = √3/2 a
h = √3/2 * 2√2 = √6
Откуда объем правильной пирамиды с четырехугольником в основании равен
V=1/3 Sh
V = 1/3 * 8 * √6 = 8√6 / 3
Ответ: 8√6 / 3 см3.
Задача.
Сторона основания правильной четырехугольной пирамиды равна а. Двугранные углы при основании равны
α. Найти площадь полной поверхности пирамиды.
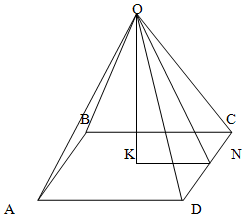
Решение.
Поскольку пирамида правильная, то ее высота проецируется в центр основания.
Значит KN = a/2
Соответственно, треугольник OKN – прямоугольный. Значит
ON = KN / cos α = a / 2cos α
Поскольку пирамида правильная, то треугольник DOC – равнобедренный. Значит его площадь равна
Sт = DC * ON / 2
Sт = ( a * a / 2cos
α) / 2 = a2 / 4cos α
Откуда площадь боковой поверхности правильной пирамиды будет равна площади всех ее боковых граней
Sб = 4a2 / 4cos
α
Sб = a2 / cos α
Откуда площадь полной поверхности равна
Sп = a2 / cos
α + a2 = a2 ( 1 + 1 / cos α )
Ответ: площадь полной поверхности правильной четырехугольной пирамиды равна a2 ( 1 + 1 / cos α )
0
Правильная пирамида с четырехугольником в основании |
Описание курса
| Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
