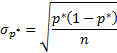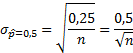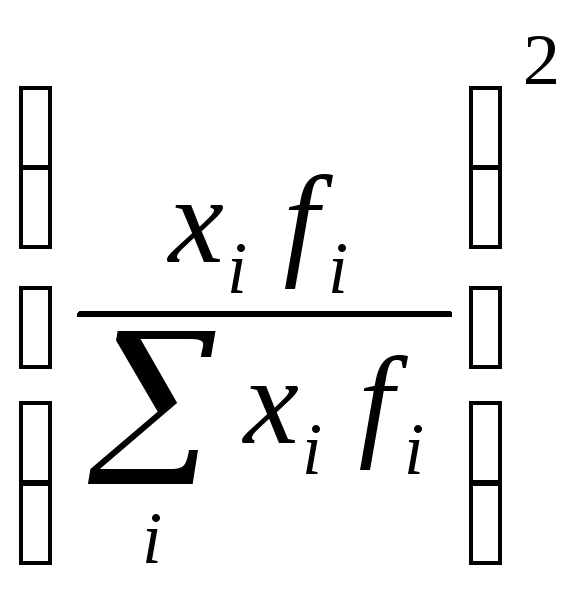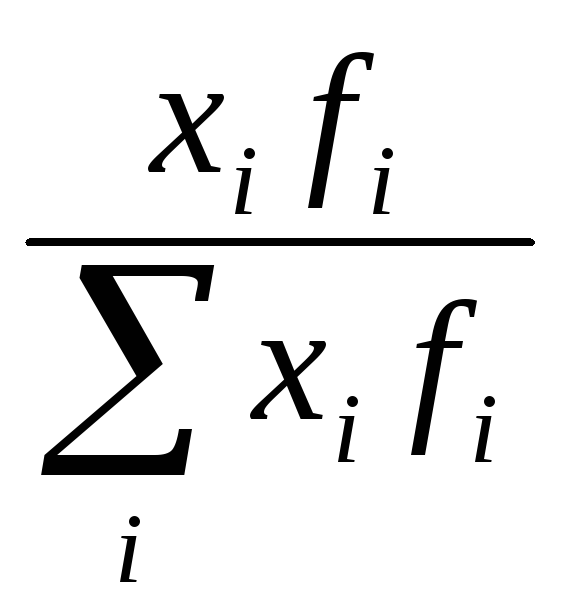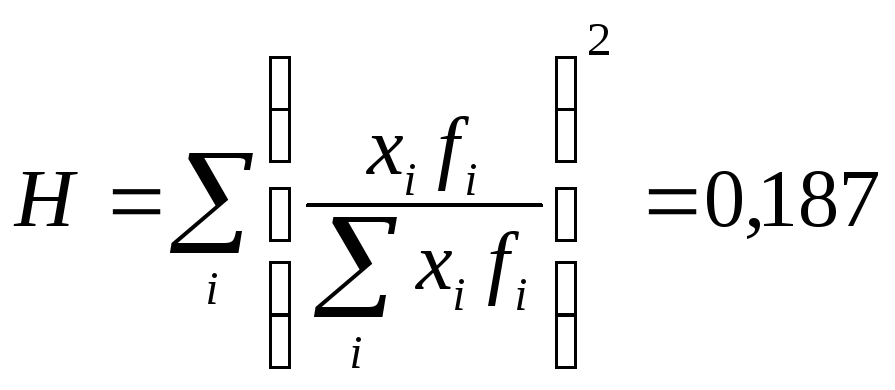Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
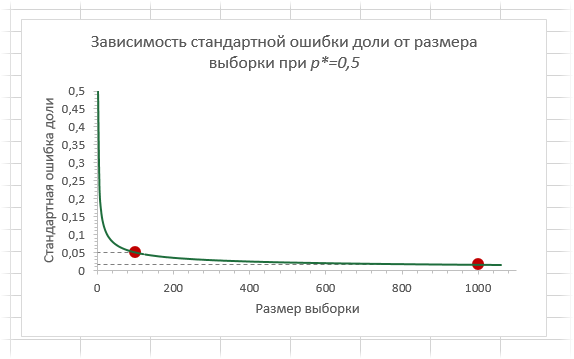
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Вариация альтернативного (качественного) признака. Правило сложения дисперсий для доли признака.
При
статистическом выражении колеблемости
альтернативных признаков наличие
изучаемого признака обозначается 1,
а его отсутствие – 0.
Доля вариантов, обладающих изучаемым
признаком обозначается р,
а доля вариантов, не обладающих признаком
q.
Следовательно, р+q=1.
Найдем их среднее
значение и дисперсию:
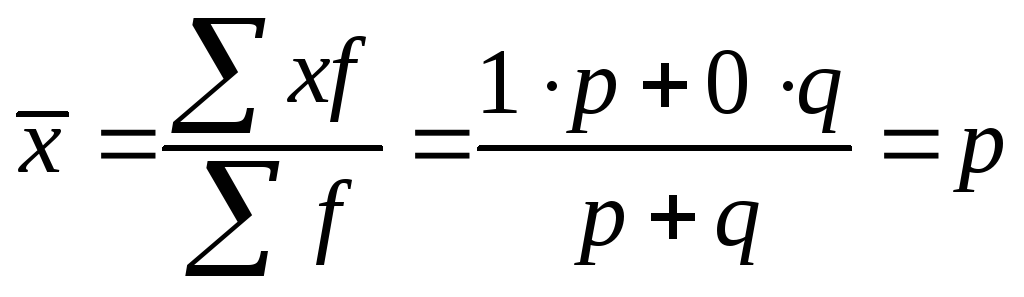
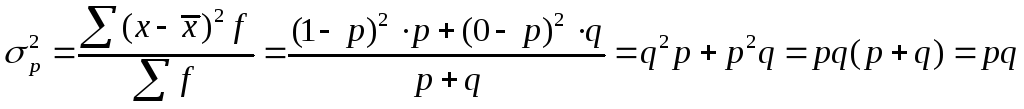
Дисперсия
альтернативного признака равна
произведению доли единиц, обладающих
признаком, и доли единиц, не обладающих
им.
Пример
6.3. На 10000
населения приходится 4000 мужчин и 6000
женщин. Определить среднее квадратическое
отклонение по полу.
Решение:
Доля мужчин в населении p=4000/10000=0,4;
доля женщин q=6000/10000=0,6.
Тогда дисперсия
,
а среднее квадратическое отклонение
.
Пример
6.4. Налоговой
инспекцией одного из районов города
проведено 86 проверок коммерческих фирм
и в 37 обнаружены финансовые нарушения.
Определить среднее квадратическое
отклонение числа нарушений.
Решение:
По условию n=86,
m=37,
тогда доля фирм, в которых обнаружены
нарушения, составит p=37/86=0,43;
q=1-0,43=0,57.
Дисперсия –
,
а среднее квадратическое отклонение.
Правило сложения
дисперсий распространяется и на дисперсии
доли признака, то есть доли единиц с
определенным признаком в совокупности,
разбитой на части (группы).
Внутригрупповая
дисперсия доли определяется
по формуле:
(6.21)
Средняя из
внутригрупповых дисперсий рассчитывается
так:
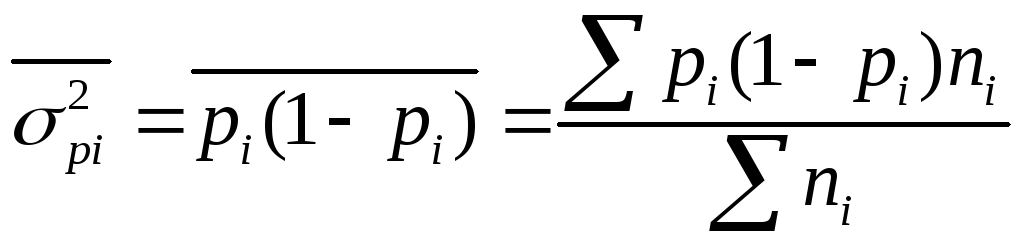
где
ni
– численность единиц в отдельных
группах;
Формула
межгрупповой дисперсии имеет следующий
вид:
(6.23)
–доля
изучаемого признака во всей совокупности,
которая определяется по формуле:
(6.24)
Общая дисперсия
определяется по формуле:
(6.25)
Три вида дисперсий
объединены между собой следующим
образом:
(6.26)
Это – правило
сложения дисперсии доли признака.
Пример
6.5. Имеются
следующие данные об удельном весе
основных рабочих в трех цехах фирмы:
|
Цех |
Удельный |
Численность |
|
1 2 3 |
80 75 90 |
100 200 150 |
|
Итого |
– |
450 |
Определить общую
дисперсию доли основных рабочих по всей
фирме, используя правило сложения
дисперсий.
Решение:
1)Определим
долю рабочих в целом по фирме (формула
6.24.).
.
2) Общая дисперсия
доли основных рабочих по фирме в целом
будет равна (формула 6.25):
.
3) Внутрицеховые
дисперсии рассчитаем, применив формулу
6.21.
4)Средняя из
внутригрупповых дисперсий будет равна
(формула 6.22.)
.
5) Межгрупповую
дисперсию определим по формуле 6.23.
.
Проверка вычислений
показывает: 0,154 = 0,15 + 0,004.
Показатели дифференциации и концентрации
Анализ вариации
в рядах распределения целесообразно
дополнить показателями
дифференциации.
Для оценки
дифференциации значений признака ряда
используются децильный
коэффициент дифференциации и коэффициент
фондов.
Децильный
коэффициент
равен отношению девятой децили к первой
децили. Децильный коэффициент широко
применяют при измерении соотношения
уровней дохода 10% наиболее обеспеченного
и 10% наименее обеспеченного населения
(в разах).
Коэффициент
фондов
равен отношению среднего уровня 10-й
децили к среднему уровню 1-й децили. Он
дает более точный уровень дифференциации.
Государственная
статистика регулярно публикует
коэффициент фондов для характеристики
дифференциации доходов. Однако в
исследовательской работе чаще используется
децильный коэффициент дифференциации.
Его применение особенно эффективно в
случае, если, например, в распределении
доходов в начале первого дециля
присутствуют крайне низкие доходы, а
десятый дециль завершается аномально
высокими доходами, которые существенно
влияют на сумму доходов в этих децилях.
В такой ситуации правильнее применять
децильный коэффициент дифференциации,
а не коэффициент фондов.
К
показателям дифференциации близки по
значению показатели концентрации:
коэффициент Джини и коэффициент
Герфиндаля.
Коэффициент
концентрации Джини
рассчитывается по формуле:
,
(6.27)
где
pi
– накопленная
доля (частость) численности единиц ряда
qi
–
накопленная доля значений признака,
приходящаяся на все единицы ряда со
значеними признака не более xi.2
Коэффициент
Джини может принимать значения от 0 до
1, поэтому результат следует разделить
либо на 100, если pi
или qi
выражен в процентах, либо на 10000, если
оба показателя выражены в процентах.
Чем больше концентрация признака, тем
ближе коэффициент Джини к 1. Коэффициент
Джини используют для характеристики
степени неравномерности распределения
совокупности (например, населения) по
уровню признака (например, доходов).
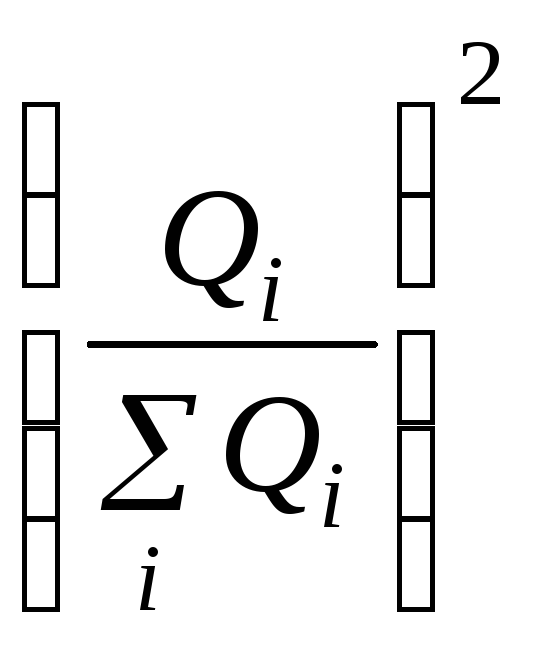
Коэффициент
Герфиндаля
вычисляется на основе данных о доле
изучаемого признака в i-той
группе в совокупном объеме признака:
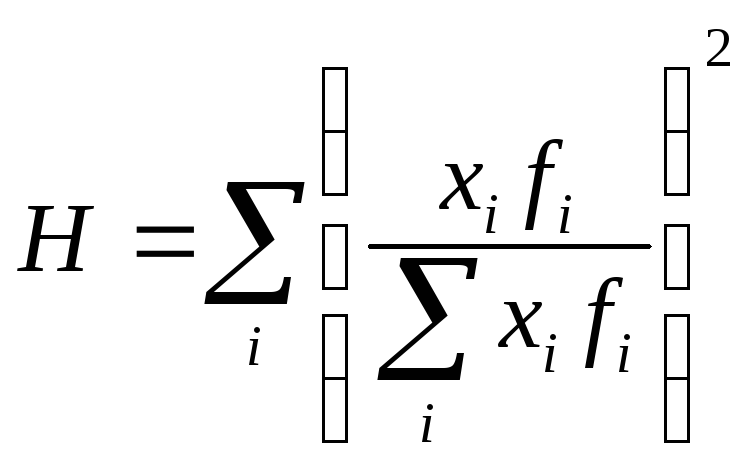
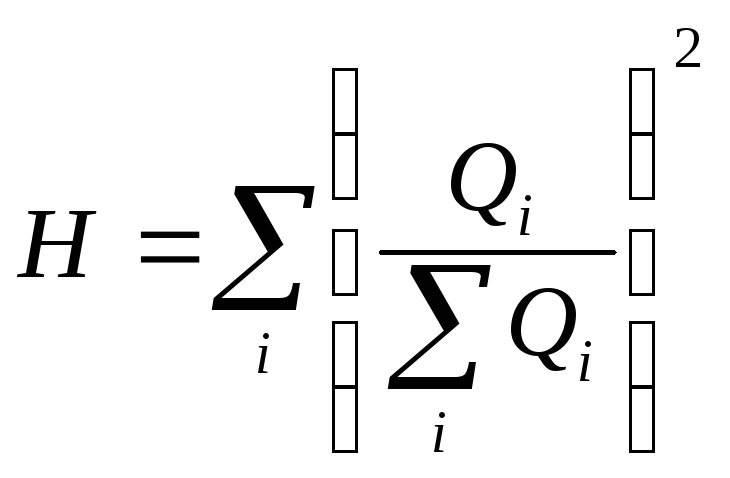
где
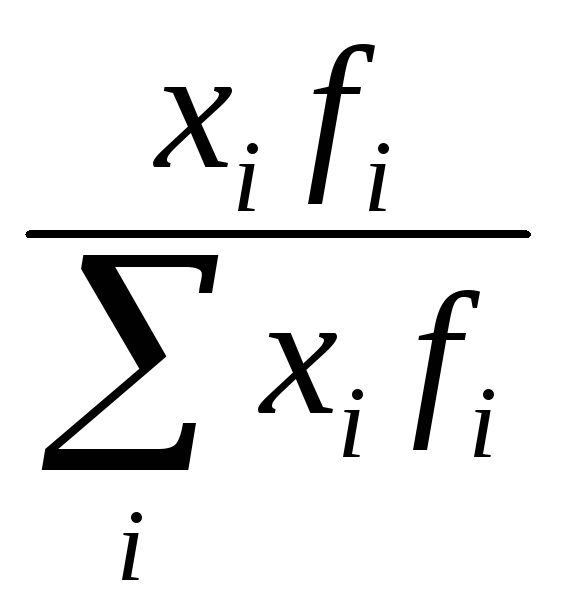
группы в общем объеме всех значений
признака;
–
объём значений признака в i–той
группе.
Показатель
Н
зависит от числа единиц в группах.
Пример
6.6. Имеются данные о полученной
балансовой прибыли 50 крупнейших банков
России (по состоянию на 01.01.1998 г.), (в
млн. руб.)
|
1 |
– |
974,2 |
11 |
– |
188,8 |
21 |
– |
143,9 |
31 |
– |
85,4 |
41 |
– |
69,3 |
|
2 |
– |
609,2 |
12 |
– |
187,3 |
22 |
– |
134,6 |
32 |
– |
84,5 |
42 |
– |
66,4 |
|
3 |
– |
588,3 |
13 |
– |
186,8 |
23 |
– |
120,9 |
33 |
– |
82,4 |
43 |
– |
66,2 |
|
4 |
– |
562,9 |
14 |
– |
171,1 |
24 |
– |
112,2 |
34 |
– |
79,6 |
44 |
– |
59,7 |
|
5 |
– |
436,3 |
15 |
– |
167,9 |
25 |
– |
108,5 |
35 |
– |
74,3 |
45 |
– |
59,1 |
|
6 |
– |
432,5 |
16 |
– |
164,3 |
26 |
– |
101,6 |
36 |
– |
74,0 |
46 |
– |
58,3 |
|
7 |
– |
283,6 |
17 |
– |
160,3 |
27 |
– |
101,3 |
37 |
– |
73,5 |
47 |
– |
57,4 |
|
8 |
– |
265,8 |
18 |
– |
159,9 |
28 |
– |
97,4 |
38 |
– |
73,2 |
48 |
– |
53,8 |
|
9 |
– |
231,5 |
19 |
– |
157,5 |
29 |
– |
97,4 |
39 |
– |
73,0 |
49 |
– |
51,4 |
|
10 |
– |
211,7 |
20 |
– |
147,6 |
30 |
– |
92,0 |
40 |
– |
71,5 |
50 |
– |
51,2 |
Величина балансовой
прибыли Сбербанка России на 01.07.97 –
4353,283 млн. руб.
-
Постройте
вариационный ряд, образовав 7-8 интервалов
произвольно. -
Рассчитайте
средний размер балансовой прибыли на
один банк на основе средней арифметической,
моды и медианы. -
Рассчитайте
показатели вариации. -
Измерьте
дифференциацию банков на основе
децильного коэффициента и коэффициента
фондов. -
Рассчитайте
коэффициент концентрации Джини и
Герфиндаля.
Решение:
1. Распределение
50 банков РФ по размеру балансовой прибыли
(БП) на 01.01.1998 г.
|
БП, млн. руб. xk-1–xk |
Коли-чество |
Сере-дина интер- вала xi |
xifi |
На-копл. час-тоты Vi |
На-копл. час-тос- ти pi |
Доля |
|
|
||
|
fi |
в % к ито- гу |
|
на- раст. ито- гом, qi |
|||||||
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
50-60 |
7 |
14 |
55 |
385 |
7 |
14 |
0,042 |
0,042 |
0,02 |
116487 |
|
60-80 |
10 |
20 |
70 |
700 |
17 |
34 |
0,076 |
0,118 |
0,006 |
129960 |
|
80-100 |
6 |
12 |
90 |
540 |
23 |
46 |
0,059 |
0,177 |
0,003 |
53016 |
|
100-150 |
8 |
16 |
125 |
1000 |
31 |
62 |
0,109 |
0,286 |
0,012 |
27848 |
|
150-300 |
13 |
26 |
225 |
2925 |
44 |
88 |
0,318 |
0,604 |
0,101 |
21853 |
|
300-500 |
2 |
4 |
400 |
800 |
46 |
92 |
0,087 |
0,691 |
0,008 |
93312 |
|
500-800 |
3 |
6 |
650 |
1950 |
49 |
98 |
0,212 |
0,902 |
0,045 |
651468 |
|
800-1000 |
1 |
2 |
900 |
900 |
50 |
100 |
0,098 |
1,0 |
0,010 |
512656 |
|
Итого |
50 |
100 |
– |
9200 |
– |
– |
1 |
– |
0,187 |
1606600 |
2. Средние показатели:
а) средний размер
балансовой прибыли на один банк рассчитаем
по средней арифметической взвешенной
б) моду рассчитаем
по формуле (5.6)
Модальный интервал
– 150-300, т.к. частота этого интервала,
равная 13, является максимальной.
в) медиану рассчитаем
по формуле (5.5)
Медианный
интервал – 100-150, т.к. накопленная частота
этого интервала, равная 31, – первая
накопленная частота, превышающая
половину суммы частот ряда.
3. Показатели
вариации:
а) дисперсия (по
формуле 6.6)

б) среднее
квадратическое отклонение (по формуле
6.7)
в) коэффициент
вариации (по формуле 6.11)
V>35%,
что
свидетельствует о неоднородности
совокупности.
4. Показатели
дифференциации:
а) для нахождения
децильного коэффициента определим
вначале первый и девятый децили по
формуле 5.4
Интервал,
соответствующий первому децилю – 50-60,
т.к. накопленная частота этого интервала,
равная 7, первая накопленная частота,
превышающая 0,1 суммы частот.
Интервал,
соответствующий девятому децилю –
300-500, т.к. накопленная частота этого
интервала, равная 14, первая накопленная
частота, превышающая 0,9 суммы частот.
Тогда
децильный коэффициент составит:
б)
т.к. 10% самых крупных и 10% самых мелких
банков составляют одну и ту же величину
(в нашем примере
),
то фондовый коэффициент составит (по
данным исходной таблицы):
5. Показатели
концентрации:
а) коэффициент
Джини рассчитаем по формуле 6.27, произведя
предварительные расчеты
|
|
|
|
1,652 |
1,428 |
|
6,018 |
5,428 |
|
13,156 |
10,974 |
|
37,448 |
25,168 |
|
60,808 |
55,568 |
|
82,984 |
67,718 |
|
98 |
90,02 |
|
|
|
б) коэффициент
Герфиндаля определим по формуле 6.28 (см.
итог гр 9):
Пример 6.7.
Для иллюстрации принципа расчета
коэффициентов Джини и Герфиндаля
воспользуемся данными выборочного
обследования дневной выручки 20 продуктовых
магазинов (тыс. руб):
|
Номера мага-зинов i |
Значения признака хi |
Накоп-ленные |
Накоп-ленная значений признака qi |
Накоп-ленная pi |
|
|
|
|
1 |
9 |
9 |
0,022 |
0,05 |
0,002 |
– |
0,0005 |
|
2 |
9 |
18 |
0,044 |
0,1 |
0,007 |
0,002 |
0,0005 |
|
3 |
11 |
29 |
0,071 |
0,15 |
0,014 |
0,007 |
0,0007 |
|
4 |
12 |
41 |
0,1 |
0,2 |
0,025 |
0,015 |
0,0009 |
|
5 |
15 |
56 |
0,137 |
0,25 |
0,041 |
0,027 |
0,0013 |
|
6 |
16 |
72 |
0,176 |
0,3 |
0,062 |
0,044 |
0,0015 |
|
7 |
17 |
89 |
0,218 |
0,35 |
0,087 |
0,065 |
0,0017 |
|
8 |
18 |
107 |
0,262 |
0,4 |
0,118 |
0,092 |
0,0019 |
|
9 |
19 |
126 |
0,308 |
0,45 |
0,154 |
0,123 |
0,0021 |
|
10 |
21 |
147 |
0,359 |
0,5 |
0,198 |
0,162 |
0,0026 |
|
11 |
21 |
168 |
0,411 |
0,55 |
0,246 |
0,205 |
0,0026 |
|
12 |
25 |
193 |
0,472 |
0,6 |
0,307 |
0,296 |
0,0037 |
|
13 |
25 |
218 |
0,533 |
0,65 |
0,373 |
0,320 |
0,0037 |
|
14 |
26 |
244 |
0,597 |
0,7 |
0,447 |
0,388 |
0,0040 |
|
15 |
26 |
270 |
0,66 |
0,75 |
0,528 |
0,462 |
0,0040 |
|
16 |
26 |
296 |
0,724 |
0,8 |
0,615 |
0,543 |
0,0040 |
|
17 |
26 |
322 |
0,787 |
0,85 |
0,709 |
0,630 |
0,0040 |
|
18 |
27 |
349 |
0,853 |
0,9 |
0,811 |
0,725 |
0,0044 |
|
19 |
30 |
379 |
0,927 |
0,95 |
0,927 |
0,834 |
0,0054 |
|
20 |
30 |
409 |
1,0 |
1,0 |
– |
0,95 |
0,0054 |
|
|
5,670 |
5,584 |
0,05528 |
Коэффициент
Джини равен 0,086, что свидетельствует о
невысоком уровне концентрации выручки
магазинов. Значение коэффициента
Герфиндаля, равное 0,05528, подтверждает
этот вывод.
Следует
отметить, что приведенные расчеты носят
исключительно иллюстративный характер,
поскольку экономический смысл
коэффициентов Джини и Герфиндаля
наиболее полно проявляется лишь при
проведении сравнений исследуемых
явлений во времени и в пространстве.
Например, коэффициента Джини для
характеристики дифференциации доходов
населения в различных регионах РФ или
странах, Коэффициента Герфиндаля для
характеристики концентрации производства,
капитала. Основное достоинство
коэффициента Герфиндаля – его высокая
чувствительность к изменению в суммарном
обороте долей крупнейших участников,
что позволяет отслеживать концентрацию
рыночного оборота и реагирует на число
участников рынка. Коэффициент Герфиндаля
может быть использован в качестве меры
диверсификации кредитного портфеля
банка. Чем меньше значение коэффициента
Герфиндаля, т.е. чем больше диверсифицирован
кредитный портфель, тем ниже могут быть
требования по капиталу к кредитному
портфелю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти дисперсию?
Полезная страница? Сохрани или расскажи друзьям
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Спасибо за ваши закладки и рекомендации
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Внутрифирменные дисперсии доли
Определить :
а) внутрифирменные дисперсии доли;
б) среднюю из внутрифирменных дисперсий
в) межгрупповую дисперсию;
г) общую дисперсию.
Проверить правильность произведенных расчетов с помощью правила расчета дисперсий доли.
|
Фирма |
Общая выручка, |
Международный туризм |
Доля |
|
1 |
150 |
120 |
0,8 |
|
2 |
200 |
180 |
0,9 |
|
3 |
400 |
380 |
0,95 |
|
Итого |
750 |
680 |
|
|
Среднее |
250 |
226,667 |
0,883 |
а) Внутрифирменная дисперсия доли определяется по формуле:
б) Средняя из внутрифирменных дисперсий определяется по формуле:
в) Межгрупповая дисперсия определяется по формуле:
г) Находим общую дисперсию по правилу сложения:
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.