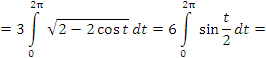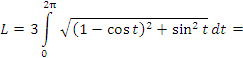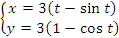
Решение. Заметим, что параметр t принимает на концах первой арки циклоиды значения 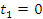
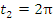
Учитывая, что 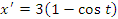
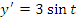
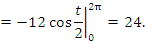
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: найти длину арки циклоиды
|
|||
|
Найти длину арки циклоиды, заданной параметрически [math]begin{cases}x=a(t-sin{t}),\y=a(1-cos{t})end{cases}[/math] Решение: [math]begin{cases}x’=dfrac{dx}{dt}=a(1-cos{t}),\[8pt]y’=dfrac{dy}{dt}=asin{t}.end{cases}[/math] Следовательно, [math]l=intlimits_{0}^{2pi}!sqrt{a^2(1-cos{t})^2+a^2 sin^2{t}},dt[/math] Помогите решите интеграл.
|
||
| Вернуться к началу |
|
||
|
vvvv |
Заголовок сообщения: Re: найти длину арки циклоиды
|
|
Prihod писал(а): Найти длину арки циклоиды, заданной параметрически [math]begin{cases}x=a(t-sin{t}),\y=a(1-cos{t})end{cases}[/math] Решение: [math]begin{cases}x’=dfrac{dx}{dt}=a(1-cos{t}),\[8pt]y’=dfrac{dy}{dt}=asin{t}.end{cases}[/math] Следовательно, [math]l=intlimits_{0}^{2pi}!sqrt{a^2(1-cos{t})^2+a^2 sin^2{t}},dt[/math] Помогите решите интеграл. Выражение под радикалом упрощается (радикал исчезает) и интеграл берется легко.
|
|
| Вернуться к началу |
|
| За это сообщение пользователю vvvv “Спасибо” сказали: Prihod |
|
|
Prihod |
Заголовок сообщения: Re: найти длину арки циклоиды
|
|
распишите пожалуйста, не легко для меня
|
|
| Вернуться к началу |
|
|
Prihod |
Заголовок сообщения: Re: найти длину арки циклоиды
|
|
[math]l=intlimits_{0}^{2pi}!sqrt{a^2(1-cos{t})^2+a^2 sin^2{t}},dt=aintlimits_{0}^{2pi}!sqrt{2-2cos{2t}},dt=aintlimits_{0}^{2pi}!sin{frac{t}{2}},dt=8a[/math] верно на решал?
|
|
| Вернуться к началу |
|
|
Prihod |
Заголовок сообщения: Re: найти длину арки циклоиды
|
|
опечатка [math]sqrt{a^2(1-cos{t})^2+a^2 sin^2{t}}=sqrt{a^2(1-2cos{t}+cos^2{t}+sin^2{t}})=asqrt{2-2cos{t}}[/math]
|
|
| Вернуться к началу |
|
|
DerW |
Заголовок сообщения: Re: найти длину арки циклоиды
|
| Вернуться к началу |
|
Рассмотрим плоскую
линию АВ,
заданную параметрическими уравнениями
где
и
– непре-рывные функции. Такую кривую
называют простой, если различным
значениям параметра соответствуют
различные точки кривой, за исключением
значенийи
,
которым может соответствовать одна
точка в случае замкнутой кривой. Простой
линией является, например, график функции.
Разобьем эту линию
точками
наn
частей и соединим соседние точки
отрезками прямых. Получим n–звенную
ломанную, вписанную в линию АВ.
Длину k-го
звена ломанной обозначим
(это
расстояние между точкамии
).
Длину наибольшего звена обозначим.
Периметр ломанной:.
Определение.
Если при
существует конечный предел
,
то:1)
линиюАВ
называют спрямляемой; 2) число l
называют длиной линии.
II Явное задание линии
Теорема 1.
Пусть АВ
– это график
непрерывно-дифференцируемой функции
.
Такая линия спрямляема и её длина
вычисляется по формуле
(1)
Доказательство.
Для определенности считаем, что точка
А
имеет координаты
,
а точкаВ
–
.
Обозначим черезкоординаты точки
,
так что абсциссы этих точек дают разбиение
отрезка[a,b]:
.
Длинаk-го
звена ломанной
Как обычно обозначим
,
а к приращению функции применим теорему
Лагранжа:
.
Следовательно,
.
Длина всей ломанной
представляет собой
интегральную сумму для функции
.
Kроме
того, условие
равносильно
.
В силу условий теоремы функцияF(x)
непрерывна, следовательно, интегрируема.
Поэтому
,
т.е. длина линииАВ,
есть не
что иное, как
интеграл в правой части формулы (1).
Теорема доказана.
Пример 1.
Вычислить длину части полукубической
параболы
,
расположенной внутри параболы.
Решение.
Находим точки пересечения линий:
(корень
– посторонний, ибо линии распо-
х
ложены в правой полуплоскости).
Уравнения
линий
не изменяются при замене
на(–
y).
Это
означает
симметрию относительно оси Ox.
Поэтому
достаточно вычислить длину части ли-
линии,
лежащей в 1-й четверти. Здесь полукуби-
ческая
парабола – это график функции
.
Подготовительные
вычисления
Итак, искомая
длина:

Замечание 1.
Если линия АВ
задана явным уравнением
то её длина выражается формулой
III Параметрическое задание линии
Теорема 2.
Пусть простая линия АВ
задана параметрическими уравнениями
причем функции
и
– непрерывно-дифференцируемы. Тогда
линия спрямляема и ее длину можно
вычислить по формуле
(2)
Доказательство.
Обозначим абсциссы крайних точек линии
и пусть
.
Для упрощения доказательства будем
считать, чтона
,
а, следовательно (в силу непрерывности),
сохраняет знак. Условиеозначает возрастание функции
.
Значити
.
В формуле (1) сделаем замену переменной
.
Тогда
и
,
а формула (1) принимает вид
Элементарные
преобразования приводят нас к формуле
(2).
Если же
,
то
убывает на
и
.
Та же замена
приведет нас к соотношению
Изменение направления
интегрирования (от
до
)
снова приведет нас к формуле (2). Теорема
доказана.
Заметим, что есть
доказательства формулы (2), не использующие
условие знакопостоянства
.
Но они очень громоздкие и используют
такие свойства непрерывных функций,
которые находятся за пределами нашей
программы.
Пример 2.
Вычислить длину одной арки циклоиды
Циклоида – это
плоская кривая, которую описывает
фиксированная точка окружности радиуса
R,
катящаяся без скольжения по прямой
линии.
Решение.
Первая арка циклоиды соответствует
изменению параметра от 0 до
.
Вычислим производныеи
и найдем сумму их квадратов:
Заметим,
что
,
ибо.
Имеем для искомой длины:
Замечание 2.
Формула (2) естественным образом обобщается
на случай пространственных линий
:
Пример 3.
Найти длину одного витка винтовой линии
Решение.
Первый виток соответствует изменению
параметра от 0 до
.
Имеем для длины:
Соседние файлы в папке MATANALIZ – 2
- #
- #
- #
- #
- #
Ответы Mail.ru
Домашние задания
Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика
Другие предметы
Вопросы – лидеры.
Ответьте на вопросы по микробиологии.
1 ставка
Срочно! Не могу разобраться с ответом
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
l0v3r m48~~
Ученик
(124),
закрыт
13 лет назад
Лучший ответ
Miha Zinkovsky
Мастер
(1312)
13 лет назад
у вас в условии опечатка. Вот решение с правильным условием:
Остальные ответы
Похожие вопросы
Длина дуги кривой
Содержание:
- Длина дуги в прямоугольных координатах
- Длина дуги кривой, заданной параметрически
Длина дуги кривой 


определяется формулой
Если кривая задана уравнением в полярных координатах
Длина дуги в прямоугольных координатах
Длина s дуги гладкой кривой 
абсциссами 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1.
Найти длину астроиды
Решение:
Дифференцируя уравнение астроиды, получим:
Поэтому для длины дуги одной четверти астроиды имеем:
Отсюда
Длина дуги кривой, заданной параметрически
Если кривая задана уравнениями в параметрической форме 


где 
Возможно вам будут полезны данные страницы:
Пример 2.
Найти длину одной арки циклоиды (рис. 50)


Пределы интегрирования 



где 

Пример 3.
Найти длину всей кривой 

Решение:
Имеем 

Пример 4.
Найти длину дуги астроиды 

Дифференцируя функцию 

Найдем выражение для подынтегральной функции, входящей в формулу (10.18). Имеем

По формуле (10.18) находим

При 

Пример 5.
Вычислить длину дуги полукубической параболы 
Указанная дуга состоит из двух частей, симметричных относительно оси 
Вычислим длину одной из них. Находя производную функции

Пример 6.
Найти длину дуги одной арки циклоиды 

Движущаяся точка описывает одну арку циклоиды (рис. 1.35) когда 

выражение для подынтегральной функции в формуле (10.19). Дифференцируя уравнения циклоиды, получим:



Итак, 
Пример 7.
Найти длину дуги эвольвенты (развертки) окружности: 
По формуле (10.19) получаем

Развертка окружности изображена на рис. 1.37.
Пример 8.
Найти длину дуги спирали Архимеда г — а<р от полюса О до любой точки М.
По формуле (10.20) получаем


то 
Пример 9.
Вычислить длину кривой 
Вся кривая описывается точкой при изменении 



Лекции:
- Вычислить несобственный интеграл
- Градиент функции: пример решения
- Интеграл натурального логарифма
- Критические точки и экстремумы функции
- Экстремумы функции двух переменных. Производная по направлению
- Числовые последовательности
- Уравнение прямой в пространстве
- Непрерывность функции
- Уравнение плоскости
- Отрицательное биномиальное распределение