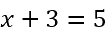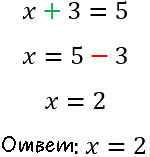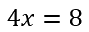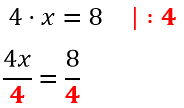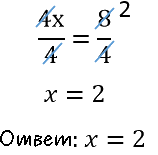п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x – 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x – (3 – 2x) = 9
Решение:
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
Проверка:
$4 -(3 – 2 cdot 4)=9 implies 4 – 3 + 8 = 9 implies 9 equiv 9$
Ответ: x = 4
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
Решение:
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 – 3 $iff$ x=5
Проверка:
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Ответ: x = 5
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
Решение:
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 – 4 $iff$ 3x = 24 $iff$ x=8
Проверка:
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Ответ: x = 8
Пример 4. Решите уравнение $ frac{3x-7}{3} – frac {5x-11}{5} = 0$
Решение:
$frac {3x-7}{3} – frac {5x-11}{5} = 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Решений нет.
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac {2x – 7}{2} = frac {3x+6}{3}$
Решение:
$frac {2x-7}{2}=frac {x+6}{3} | times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac {33}{4} =8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Решение:
$$|x+1|=5 iff left[ begin{array}{cc} {x+1=-5}\ {x+1=5} end{array} right. iff left[ begin{array}{cc} {x=-5-1}\ {x=5-1} end{array} right. iff left[ begin{array}{cc} {x_1=-6}\ {x_2=4} end{array} right. $$
Ответ: $ x_1=-6, x_2=4$
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
Решение:
$$ |x + 1| = x + 3 iff left[ begin{array}{cc} {left{ begin{array}{c} x+1 ge 0 \ x+1=x+3 end{array} right.}\ {left{ begin{array}{c} x+1<0 \ -(x+1)=x+3 end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} x ge -1 \ 1=3 end{array} right.}\ {left{ begin{array}{c} x<-1 \ -x-1=x+3 end{array} right.} end{array} right. iff $$
$$ iff left[ begin{array}{cc} {emptyset}\ {left{ begin{array}{c} x<-1 \ -x-x=3+1 end{array} right.} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {-2x=4} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {x=-2} end{array} right. iff x=-2 $$
Проверка:
$$|-2+1|=-2+3 implies |-1|=1implies 1 equiv 1$$
Ответ: x = -2
Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Решение:
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 – 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
a=1
Ответ: a = 1
Вопросы
занятия:
· ввести понятия «уравнение с
одной переменной», «решение уравнений с одной переменной»;
· разобрать что значит «решить
уравнение»;
· ввести понятие равносильных
уравнений.
Материал
урока
Рассмотрим следующую задачу.
К заданному числу прибавили
9 и получили в сумме 25. Какое число задумано?
Обозначим букой х
задуманное число. Тогда по условию задачи
х + 9 = 25
То есть, чтобы найти
неизвестное число, мы составили равенство, которое содержит переменную х.
Равенства такого вида называются уравнениями с одной переменной.
Теперь надо найти такое
значение переменной х, при подстановке которого в наше уравнение
получается верное числовое равенство. Для этого переносим 9 в правую часть
равенства и получаем:
х = 25 – 9.
х = 16
То есть 16 и есть
задуманное число.
Найденное значение
переменной х называется решением уравнения, или корнем
уравнения.
Таким образом, можем
сформулировать следующие определения.
Равенство, содержащее
одну переменную, называется уравнением с одной переменной, или уравнением
с одним неизвестным.
Значение переменной,
при котором уравнение превращается в верное числовое равенство, называется корнем
(или решением) уравнения.
Рассмотренное выше
уравнение имеет один корень.
Но есть уравнения,
которые имеют два, три, четыре и более корней или не
имеют корней вообще.
Например,
Определение.
Решить уравнение
– это значит найти все его корни или доказать, что их нет.
Определение.
Два уравнения
называются равносильными, если каждый корень первого уравнения является
корнем второго, и наоборот – каждый корень второго уравнения является корнем
первого, то есть, оба уравнения имеют одни и те же корни.
Равносильными являются
также уравнения, которые не имеют корней.
Например,
А теперь сформулируем
свойства, которые используются при решении уравнений.
Свойство 1.
Если в уравнении
перенести слагаемое из одной части в другую, изменив его знак, то получится
уравнение, равносильное данному.
Например,
Свойство 2.
Также, если обе части
уравнения умножить или разделить на одно и то же отличное от нуля число, то
получится уравнения, равносильное исходному.
Например,
Давайте решим следующие
упражнения.
Пример.
Пример.
Пример.
Пример.
Для решения линейных уравнений используют два основных правила (свойства).
Свойство № 1
или
правило переноса
Запомните!
При переносе из одной части уравнения в другую
член уравнения меняет свой знак на противоположный.
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую.
Так как
в левой части уравнения у числа «3»
был знак «+», значит в правую часть уравнения
«3» перенесется со знаком «−».
Полученное числовое значение «x = 2» называют корнем уравнения.
Важно!
Не забывайте после решения любого уравнения записывать ответ.
Рассмотрим другое уравнение.
5x = 4x + 9
По правилу переноса перенесем «4x» из правой
части уравнения в левую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака,
мы понимаем, что перед «4x» стоит знак «+».
5x = 4x + 9
5x = +4x + 9
5x − 4x = 9
Теперь приведем подобные и решим уравнение до конца.
5x − 4x = 9
x = 9
Ответ: x = 9
Свойство № 2
или
правило деления
Запомните!
В любом уравнении можно разделить левую и правую часть на одно и то же число.
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число «4», которое стоит при «x»,
называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.
Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент
«1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы
получить
«1»?».
Ответ очевиден, нужно разделить на «4».
Используем правило деления и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.
Используем сокращение дробей и решим линейное уравнение до конца.
Как решить уравнение, если «x» отрицательное
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже.
−2x = 10
Чтобы решить такое уравнение, снова зададим себе вопрос:
«На что нужно разделить «−2»,
чтобы получить «1»?». Нужно разделить на «−2».
−2x = 10 |:(−2)
=
x = −5
Ответ: x = −5
Примеры решения линейных уравнений
Рассмотрим другие примеры решения линейных уравнений. Обычно для решения уравнений нужно
применять оба свойства (правило переноса и правило деления).
Также требуется вспомнить правило раскрытия скобок и
правило приведения подобных.
-
25x − 1 = 9
25x = 9 + 1
25x = 10 |: 25=
x =
Ответ: x =
-
11(y − 4) + 10(5 − 3y) − 3(4 − 3y) = −611y − 44 +
50 −
30y − 12
+ 9y = −611y − 30y +
9y −
44 + 50 − 12 = −620y − 30y + 6 − 12 = −6
−10y − 6 = −6
−10y = −6 + 6
−10y = 0 |:(−10)
=
y = 0
Ответ: y = 0
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
4 июня 2021 в 18:53
Одинахон Иномова
Профиль
Благодарили: 0
Сообщений: 1
Одинахон Иномова
Профиль
Благодарили: 0
Сообщений: 1
Найдите корень уравнения:√39-2х=5
0
Спасибо
Ответить
2 февраля 2022 в 23:15
Ответ для Одинахон Иномова
Лопух-Бурьянович Травкин
Профиль
Благодарили: 0
Сообщений: 1
Лопух-Бурьянович Травкин
Профиль
Благодарили: 0
Сообщений: 1
√39-2x = 5
√39-5 = 2x
x = ((√39)-5):2
x = (6.2449979984 — 5):2
x = 1.2449979984: 2
x = 0.62249899919
или по формуле Герона √(a2 + b) = a +
√39-2x = 5
√39-5 = 2x
x = ((√39)-5)/2
x = (√(36+3) — 5)/2
x = (√(62+3) — 5)/2
x = ((6 +
) — 5)/2
x = (6 — 5)/2
x = 1 / 2
x =
x =
0
Спасибо
Ответить
20 апреля 2020 в 19:08
Егор Семенов
Профиль
Благодарили: 0
Сообщений: 1
Егор Семенов
Профиль
Благодарили: 0
Сообщений: 1
Найти наименьшее значение выражения: (4х²+6x+9)/3x, при x>0,
0
Спасибо
Ответить
18 августа 2020 в 1:23
Ответ для Егор Семенов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(x) = + + 2 ≥ f(1,5) = 6.
0
Спасибо
Ответить
26 марта 2020 в 16:35
Антон Манукян
Профиль
Благодарили: 0
Сообщений: 1
Антон Манукян
Профиль
Благодарили: 0
Сообщений: 1
Найдите сумму коэффициентов линейного уравнения с двумя неизвестными 3x-2y-4=0.
0
Спасибо
Ответить
20 мая 2020 в 9:40
Ответ для Антон Манукян
Сергей Глазов
Профиль
Благодарили: 0
Сообщений: 1
Сергей Глазов
Профиль
Благодарили: 0
Сообщений: 1
3-2-4=-3
0
Спасибо
Ответить
21 декабря 2016 в 14:00
Даня Буйновский
Профиль
Благодарили: 0
Сообщений: 1
Даня Буйновский
Профиль
Благодарили: 0
Сообщений: 1
0,6x+0.42=0 решите пж уравнение
0
Спасибо
Ответить
11 февраля 2017 в 16:25
Ответ для Даня Буйновский
Алексей Карапов
Профиль
Благодарили: 0
Сообщений: 9
Алексей Карапов
Профиль
Благодарили: 0
Сообщений: 9
0.6 · ?0.7 +0.42 =0
Так как 0.6 · ?0.7 = ?0.42, а ?0.42 +0.42 =0
0
Спасибо
Ответить
11 сентября 2016 в 23:15
Антон Ершов
Профиль
Благодарили: 0
Сообщений: 2
Антон Ершов
Профиль
Благодарили: 0
Сообщений: 2
?ЗАДАНИЕ: Найдите корень уравнения?
(P.S) Мне нужно полностью всё решение. Заранее — спасибо.
1) 0,9x ? 0,6 (x ? 3) = 2 (0,2x ? 1,3)
2) ? 0,4 (3x ? 1) + 8 (0,8x ? 0,3) = 5 ? (3,8x + 4)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
Спасибо! Решено!
0
Спасибо
Ответить
19 сентября 2016 в 14:52
Ответ для Антон Ершов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1)0,9x ? 0,6x + 1,8 = 0,4x ? 2,6
0,1x=4,4
x=44
2) ?1,2 +0,4 +6,4x ?2,4 =5 ?3,8x ?4
9x =3
x=
0
Спасибо
Ответить
16 сентября 2015 в 11:06
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
?2x ? 3y=1
?3x + y=7
Помогите Пожалуйста!)
0
Спасибо
Ответить
5 сентября 2016 в 15:32
Ответ для Макс Простов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
2 уравнения, 2 неизвестных. Выразим y через x и подставим в первое выражение. Найдя ответ, подставим в полученное значение x.
3x +y=7
y=7 ? 3x
2x ?3(7 ?3x)=1
2x ?21 +9x=1
11x=22
x=2
y=7 ?3 · 2 = 1
Проверка:
2 · 2 ?3 · 1=1
3 · 2 +1=7
Верно
Ответ: x=2, y=1.
0
Спасибо
Ответить
16 сентября 2015 в 10:32
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
Макс Простов
Профиль
Благодарили: 0
Сообщений: 4
1. 2x? ?7x +3
2. 3x? +5x ?2
0
Спасибо
Ответить
5 сентября 2016 в 15:28
Ответ для Макс Простов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
1) D=49 ? 4 · 3 · 2 = 25
x1= = = 3
x2===0,5
Проверка:
2 · 0,52 ? 7 · 0,5 + 3 = 0
0=0
2 · 32 ? 7 · 3 + 3 = 0
0=0
2) D=25 ?4 · 3 · (-2) = 25 + 24 = 49
x1=
x2=-2
проверка аналогично.
0
Спасибо
Ответить
13 сентября 2015 в 12:33
Киара Артуровна
Профиль
Благодарили: 0
Сообщений: 1
Киара Артуровна
Профиль
Благодарили: 0
Сообщений: 1
2х-1
2х+1=2х+1
2х-1 + 8
1-4х2
0
Спасибо
Ответить
5 сентября 2016 в 13:39
Ответ для Киара Артуровна
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
4x2 + 2x ? 1 ? 2x + 1 ? 2x ? 1 + 2x + 1 ? 8 + 1 = 0
4x2? 7 = 0
4x2=7
x2=
x=±?()
0
Спасибо
Ответить
28 апреля 2015 в 13:19
Дарья Баширова
Профиль
Благодарили: 0
Сообщений: 1
Дарья Баширова
Профиль
Благодарили: 0
Сообщений: 1
Как решить?
х+3х=9.7*3х
0
Спасибо
Ответить
16 апреля 2016 в 8:42
Ответ для Дарья Баширова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
X+3X=9,7 · 3X
4X=29,1X
33,1Х=0
Х=0
Проверка:
0+3 · 0 = 9,7 · 3 · 0
0=0
Ответ: Х=0
0
Спасибо
Ответить
Уравнение и его корни: определения, примеры
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня – 2 , 1 и 5 , то пишем – 2 , 1 , 5 или < – 2 , 1 , 5 >.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Уравнение и его корни
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x – 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x – (3 – 2x) = 9
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
$4 -(3 – 2 cdot 4)=9 implies 4 – 3 + 8 = 9 implies 9 equiv 9$
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 – 3 $iff$ x=5
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 – 4 $iff$ 3x = 24 $iff$ x=8
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Пример 4. Решите уравнение $ frac<3x-7> <3>- frac <5x-11> <5>= 0$
$frac <3x-7> <3>- frac <5x-11> <5>= 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac <2x – 7> <2>= frac <3x+6><3>$
$frac <2x-7><2>=frac <3>| times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac <33> <4>=8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
$$ |x + 1| = x + 3 iff left[ begin <left< begin x+1 ge 0 \ x+1=x+3 end right.>\ <left< begin x+1 Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 – 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
Решение простых линейных уравнений
О чем эта статья:
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:
если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;
если а = 0 — уравнение корней не имеет;
если а и b равны нулю, то корнем уравнения является любое число.
Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.
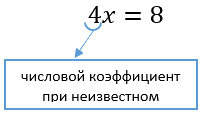
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
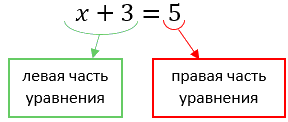
Для примера рассмотрим простейшее уравнение: x+3=5.
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12
-
Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.
-4x = 12 | : (-4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
ЮПеренести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/7-klass/uravnenie-i-ego-korni/
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
[/spoiler]
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t, r, m др., но чаще всего используются x, y, z. Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x=5, y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x+7=38, z−4=2, 8·t=4, 6:x=3.
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7·(x−1) =19, x+6·(x+6·(x−8))=3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x+2+4·x−2−x=10. Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x·(8+1)−7=8, 3−3=z+3 или 8·x−9=2·(x+17).
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x+3=6·x+7 – это уравнение с переменной x, а 3·y−1+y=0 – уравнение с переменной y.
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3,7·x+0,6=1 является уравнением с одной переменной x, а x−z=5 – уравнением с двумя переменными x и z. Примером уравнения с тремя переменными может быть выражение x2+(y−6)2+(z+0,6)2=26.
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a+1=5 мы заменим букву числом 2, то равенство станет неверным, а если 4, то получится верное равенство 4+1=5.
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a+1=5. Согласно определению, корнем в данном случае будет 4, потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2+1=5.
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0·x=5. Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0.
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x−2=4 есть только один корень – шесть, в x2=9 два корня – три и минус три, в x·(x−1)·(x−2)=0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅. Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня -2, 1 и 5, то пишем -2, 1, 5 или {-2, 1, 5}.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y, а корнями являются 2 и 7, то мы пишем y=2 и y=7. Иногда к буквам добавляются нижние индексы, например, x1=3, x2=5. Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N, целых – Z, действительных – R. Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x∈Z, а если любое действительное от единицы до девяти, то y∈1, 9.
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x+y=7, которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4, то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как (3,4).
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.