Как найди масштаб квадрата

Задание 230.

На плане изображён квадрат в масштабе 3:1. Какова длина стороны этого квадрата в действительности? Начертите его.

Ответ:

6:3=2 см – длина квадрата в действительности.

Задание 231.

Масштаб карты 1: 100 000. Расстояние между двумя посёлками на карте равно 8 см. Каково это расстояние в действительности?

Ответ:

800 км.

Задание 232.

Расстояние между городами А и В равно 80 км. Из этих городов выехали одновременно два поезда — один на запад, а другой на восток. Скорость поезда, идущего на запад, равна 70 км/ч, а скорость поезда, идущего на восток, — 65 км/ч. На каком расстоянии один от другого будут поезда через 3 ч после начала движения?

Ответ:

75+65=135 км –скорость удаления поездов

135*3=405 км – отъедут оба за 3 часа

405+80=485 км.

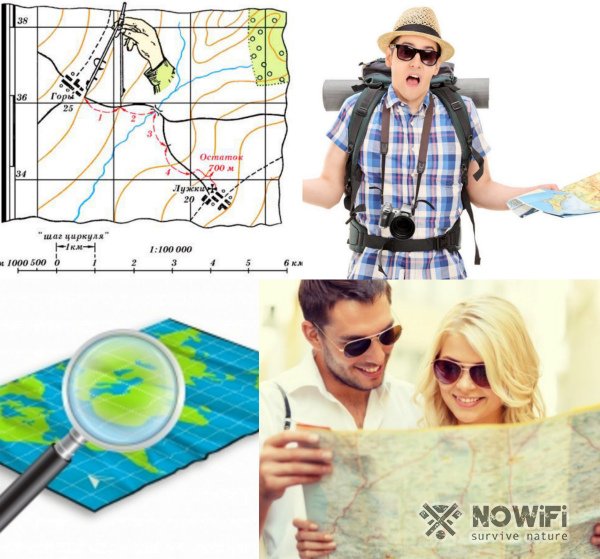
Отравляясь в лес или поход, мы всегда берем с собой карту. Именно с ее помощью туристы определяют свое местоположение на местности и прокладывают маршрут. Естественно, расстояния на картах показаны не в реальных показателях, а в определенном масштабе.

Соответственно, чтобы научиться читать карту, нужно знать, как определить масштаб в каждом конкретном случае. Именно этому вопросу и будет посвящена сегодняшняя статья.

Пошаговая инструкция, как определить масштаб

Обычно составитель указывает линейный или численный масштаб чертежа или карты, с помощью которого и определяется расстояние между объектами на местности. Но иногда топографическая карта не содержит этой информации, и определять масштаб приходится самостоятельно. В этом пригодятся некоторые знания в географии (рисунок 1).

На самом деле вычисление масштаба – простая задача, если знать, как правильно действовать. Из инструментов вам понадобится сама карта и линейка.

Самый простой способ определить масштаб – использовать километровую сетку. Она проставлена на любой карте, а стороны каждого квадрата соответствуют определенному количеству километров.

Узнать это расстояние можно по подписям у выхода линий сетки к краям карты. Например, на подписи указано, что расстояние между двумя линиями сетки составляет 1 км. Теперь измерьте это расстояние линейкой. Предположим, вы получили показатель в 2 см. Соответственно, каждый сантиметр карты соответствует 500 метрам на местности, а сам масштаб чертежа составляет 1:50000.

Понятие и виды масштабов

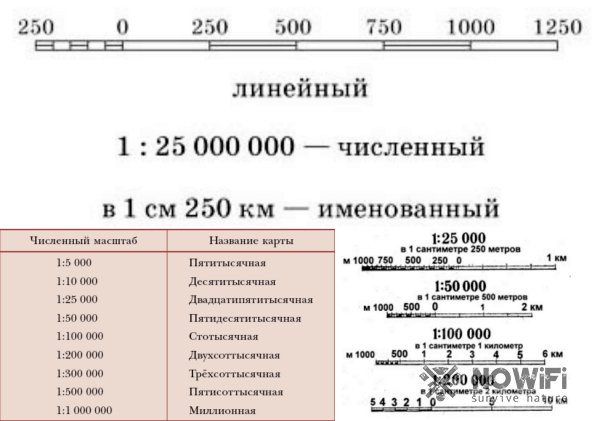
Чтобы научиться правильно вычислять масштаб, будет нелишним ознакомиться с самыми определением этого понятия. Итак, с научной точки зрения масштаб – это определенный показатель, по которому длина отрезка на карте, плане или схеме топосъемки соответствует действительной длине этого же отрезка на местности (рисунок 2).

Существует несколько видов масштаба:

1. Численный: масштаб, выполненный в виде дроби. В нем числитель – это всегда единица, а знаменатель – число, отображающее, во сколько раз уменьшено расстояние на карте.
2. Линейный: масштаб, облегчающий ориентирование. Он представляет собой специальную мерную линейку, которую наносят на карты для облегчения вычисления расстояний на местности.
3. Поперечный масштаб: используется для максимально точных измерений. Обычно его гравируют на металлических линейках, которые так и называют масштабными.

Самым простым считается именнованный или словесный масштаб. В данном случае на изображении карты просто указано, какому расстоянию соответствует 1 см плана (например, в 1 см 5 км).

Параметры точности масштаба

Точность масштаба на чертеже ограничена расстоянием в 0,01 см. Количество метров, соответствующее этому показателю на местности, и называется определением «графическая точность».

Чтобы узнать этот показатель, нужно воспользоваться градусной сеткой и провести некоторые вычисления. Лучше всего использовать численный масштаб. Берем его знаменатель и делим на 10 000, поскольку 1 см плана содержит 10 тысяч отрезков по 0,01 см. Полученное число и будет соответствовать размеру точности.

Например, если карта имеет масштаб 1:25 000, его точность на местности будет составлять 2,5 метра, а для схемы 1:100 000 – 10 метров и так далее.

Способ определения масштаба

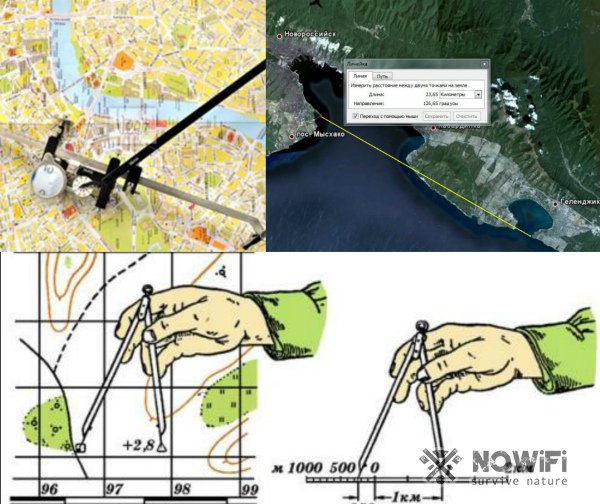
В начале статьи мы уже описывали, как можно определить масштаб изображения с помощью километровой сетки и линейки. Но есть и другие способы установить степень уменьшения и масштабирование на конкретном плане местности (рисунок 3).

Туристы обычно пользуются такими методами:

1. Номенклатура карты: чтобы воспользоваться данным способом, нужно внимательно рассмотреть реквизиты карты. Фактически, номенклатура – это буквенно-числовое название листа. У каждого масштабного ряда есть свое обозначение. Например, М-35 соответствует масштабу 1:1000000, а М-35-18-А-6-1 – 1:10000. Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения.
2. Известные расстояния: в данном случае на карте нужно найти изображения километровых столбов, которые обычно устанавливают на шоссе. Прямо на карте нужно измерить расстояние между ними. В данном случае количество сантиметров на карте будет соответствовать одному километру на местности.
3. Дуга меридиана: одна минута по меридиану соответствует 1,85 км, хотя обычно эту цифру округляют до 2 км. На боковой рамке любой карты есть подписи минут и градусов, а для выделения каждой минуты используется шашечка. Если длина одной минуты равна 3,7 см, то масштаб будет составлять 1:5000, то есть одному сантиметру на карте будет соответствовать 0,5 км на местности.

На картах с масштабом 1:2000000 обычно указывается расстояние между определенными населенными пунктами в километрах. В данном случае, для определения масштаба нужно измерить расстояние на карте линейкой. Потом расстояние, указанное в километрах, следует разделить на полученное число в сантиметрах. В результате у вас получится число, которое будет соответствовать количеству километров в одном сантиметре.

Правила оформления

Если топографическая карта местности была изготовлена правильно, на ней должен обязательно быть указан масштаб. Исключение могут быть только самодельные карты или планы местности, нарисованные вручную. Во всех остальных случаях масштаб должен быть оформлен согласно ГОСТу.

Если карта была составлена правильно, находить даже уменьшенные объекты не составит труда, ведь все измерения точно соответствуют расположению на местности.

Порядок определения масштаба на готовом чертеже

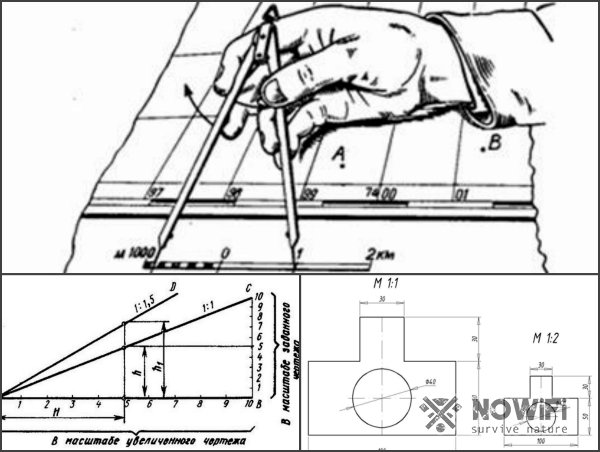
Масштаб нужно не только для того, чтобы определить расстояние на карте. Он также используется при составлении чертежей (рисунок 4).

Важно правильно выбрать масштаб для чертежа детали. Например, небольшие или сборные элементы лучше выполнять в натуральную величину, то есть в масштабе 1:1. Но иногда, для удобства чтения объект, нарисованный на бумаге, уменьшают или увеличивают.

Узнать масштаб чертежа несложно, так как он определяется примерно так же, как и географический.  В первую очередь нужно внимательно изучить чертеж. Согласно ГОСТу, масштаб должен быть указан в правом нижнем углу. При этом в машиностроении и приборостроении обычно используют увеличение, а на строительных чертежах – уменьшение.

Если по каким-то причинам вы не можете найти масштаб на готовом чертеже невозможно, можно попытаться определить его. Если под рукой есть деталь, можно просто измерить ее штангенциркулем. Также можно определить масштаб по габаритным размерам детали, указанным на чертежах.

Советы бывалых

В целом, масштаб карты и топосъемки можно смело назвать весьма полезным понятием. На первый взгляд может показаться, что определять масштаб и ориентироваться с его помощью на местности сложно.

На самом деле, если научиться высчитывать расстояние, отображенное на карте, и соотносить его с объектами на местности, то отклонение будет составлять всего несколько метров.

Детальную информацию по определению масштаба вы найдете в видео.

Всем здравствуйте! Решила рассмотреть несколько задачек на масштаб – оказалось, есть такая нужда у моих учеников. Может, и вам пригодится!

Всем нам знакомы карты местности – так или иначе, но каждый встречался с ними, в школе или по жизни. Понятно, что карта – лишь только изображение, и по сравнению с расстоянием на местности объекты на карте должны быть меньше (иначе зачем она нужна?). Масштаб – это как раз отношение, которое показывает, во сколько раз карта меньше, чем реальная местность, то есть во сколько раз расстояние на карте меньше, чем на местности.

Но масштаб призван также и увеличивать что-то маленькое так, чтобы можно было сделать подробный чертеж или внимательно рассмотреть что-то мелкое.

Первый, “уменьшающий”, масштаб, может быть записан, например, так: 1:5. Тогда  расстояние на карте (или чертеже) в пять раз меньше, чем в реальности. Масштаб, записанный  так: 1: 100 000  означает, что изображение меньше в сто тысяч раз.

“Увеличивающий” масштаб записывается: 100:1, или 1000:1. Это значит, что расстояние увеличили в сто или тысячу раз, чтобы его можно было изобразить.

В зависимости от конкретной задачи выбирают и масштаб: карта не должна быть слишком уж мелкой, а понятной и подробной, но в то же время не должна быть гигантской,  а простую, но небольшую деталь вовсе необязательно увеличивать в десятки раз, когда может быть достаточно и пяти.

Когда работаешь с масштабом, очень важно уметь составлять отношения (пропорции). Давайте потренируемся в этом!

1. Расстояние на местности в 20 м изображено на плане отрезком 1 см. Определите масштаб плана.

Чтобы определить масштаб, нужно узнать, во сколько раз расстояние на карте меньше, чем на местности. Для этого нужно расстояние на местности привести к тем же единицам, что и на плане:

20 м = 20*100 см=2000 см.

Тогда, если одному см на карте соответствуют 2000 см на местности, то и  масштаб 1:2000, то есть на карте длина отрезка меньше в 2000 раз.

2. Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1:300?

Так как масштаб показывает, во сколько раз карта или план меньше действительного расстояния, или, иначе говоря, во сколько дом больше своего изображения, то:

см, или 75 м.

3. Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе: а) 1:10 000 000; б) 1:2 000 000?

Обозначим за расстояние на карте. Переведем длину магистрали в сантиметры:

3140 км = 3 140 000 м = 314 000 000 см.

Тогда

По правилу пропорции см.

Изображение карты во втором масштабе – крупнее (2 миллиона меньше, чем 10). Так как отношение масштабов – 1:5, то и изображение будет крупнее в пять раз: 157 см. В этом можно убедиться, решив задачу “стандартным” способом.

4. Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной странице тетради это расстояние в масштабе одна десятимиллионная?

Снова за  обозначим расстояние на карте. Тогда

, или  см.

5. Длина железной дороги Москва – Петербург приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1:10 000 000.

Переведем километры в сантиметры:

650 км = 650 000 м = 65 000 000  см.

Обозначаем расстояние на карте неизвестной и составляем пропорцию:

, или  см.

6. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на этой карте расстояние между ними 12,6 см?

Такую задачу можно решать длинным путем: определить масштаб карты и затем найти расстояние между городами, зная масштаб.

Тогда масштаб будет таким:

А второе расстояние найдем так:

.

Почему бы тогда не упростить себе задачу, не определяя масштаб, а составить пропорцию сразу:

Отсюда  см, или 25,2 км

7. Длина детали на чертеже, сделанном в масштабе 1:3, равна 2,4 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 2:1?

Нам не нужно знать, каковы реальные размеры детали – нас об этом не спрашивают. Поэтому мы и не будем их искать, а найдем новый размер чертежа через отношение масштабов:

см

8. Площадь земельного участка изображается на плане, масштаб которого 1:250, в виде прямоугольника площадью 128 кв. см. Найдите действительную площадь этого земельного участка.

Хорошая задача. Не пугайтесь, что длина и ширина участка неизвестны – нам и не надо знать их. Однако для лучшего понимания все же обозначим их, например,  и . Тогда на карте расстояние   изображается отрезком  , а расстояние   – отрезком  . Если перемножить длину и ширину изображения участка, то получим как раз 128 кв. см. Но тогда получается, что  , или , то есть реальная площадь участка получится, если площадь изображения умножить на квадрат масштаба:  кв. см. Переведем это в кв. метры, для этого нужно разделить не на 100, а на : 800 кв. м, а если нужны квадратные километры, тогда еще на : 0,0008 кв. км.

9. Площадь земельного участка прямоугольной формы 6 га. Найдите площадь прямоугольника, изображающего этот участок на плане, масштаб которого 1:5000.

Аналогичная задача. Вспомним, что такое га: это квадрат со стороной 100 м, то есть это 10 000 кв. м. Тогда в сантиметрах это (умножаем на  ) 100 000 000 кв. см. А у нас – 600 000 000 кв. см.Поделим на масштаб в квадрате, чтобы определить площадь этого прямоугольника на карте:  кв.см.

Нетрудно догадаться, что, если бы речь шла об объеме, то масштаб пришлось бы возводить в куб: в данном случае масштаб – это коэффициент подобия. Площади относятся как квадрат коэффициента подобия, а объемы – как куб коэффициента подобия.