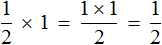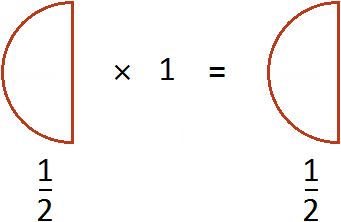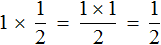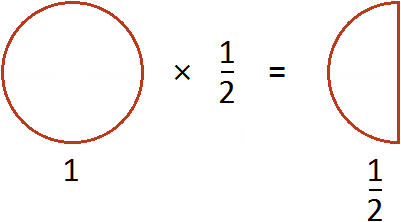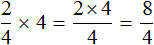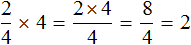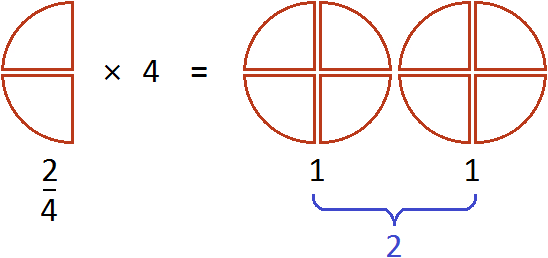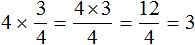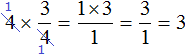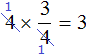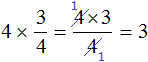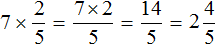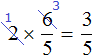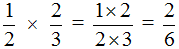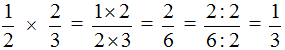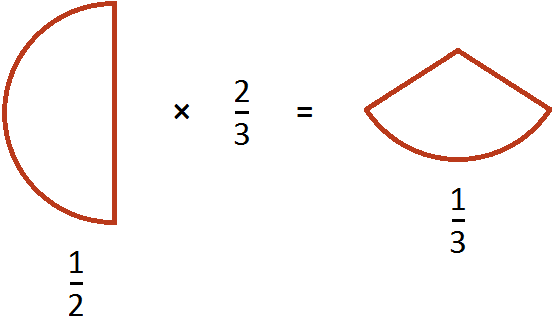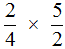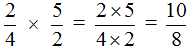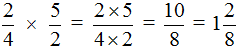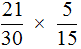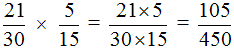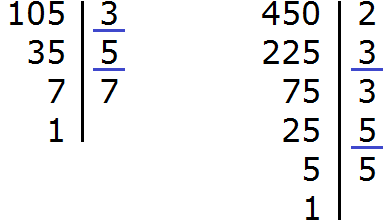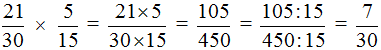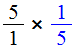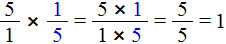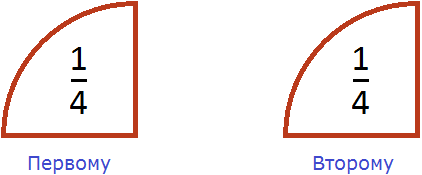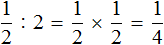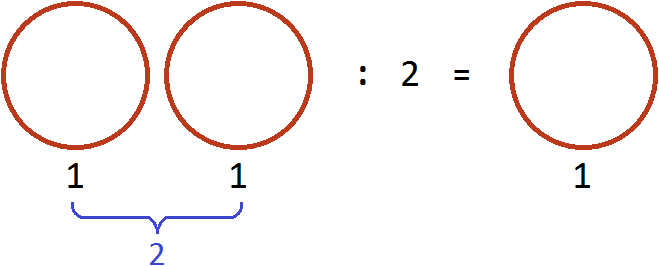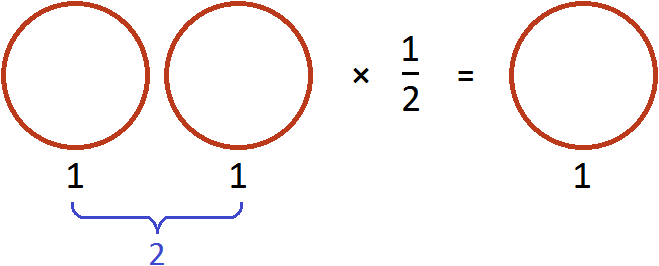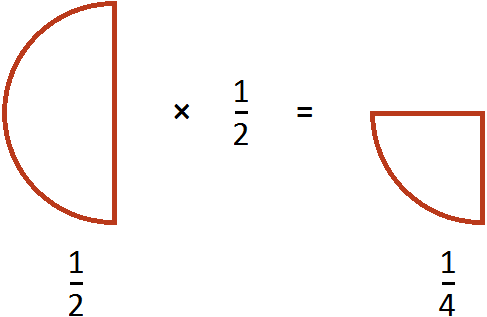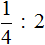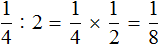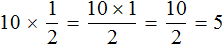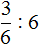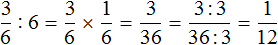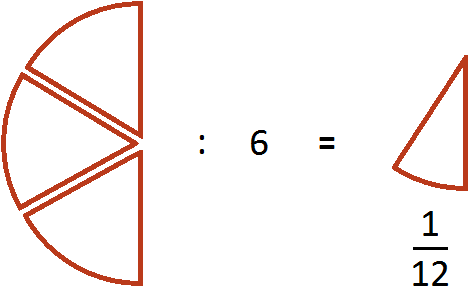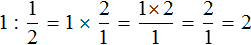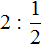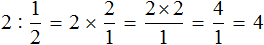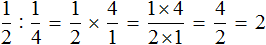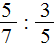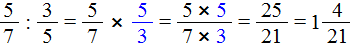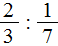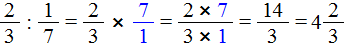Как найди обратный делитель

А вот в математике 6 класса правило : чтобы разделить одну дробь на другую надо делимое умножить на число обратное делителю?

Математика | 5 — 9 классы

А вот в математике 6 класса правило : чтобы разделить одну дробь на другую надо делимое умножить на число обратное делителю.

ЧТО ЗНАЧИТ ОБРАТНОЕ ДЕЛИТЕЛЮ?

Е перевёрнутое х обратное 1 / х

любое число, а обратное — это 1 разделить на это число и наоборот, если число 1 / х, то обратное х.

Чтобы разделить одну дробь на другую, надо вторую дробь перевернуть(знаменатель записать в числитель, а числитель в знаменатель)и потом перемножить эти дроби.

Перевёрнутая дробь и будет число обратное делителю.

Что будет если : а) и делимое и делитель умножить на 2 / 5 б) делитель разделить на 2 / 5 в) делимое умножить на 2 / 3, а делитель разделить на 2 / 3 г) делимое умножить на 7 / 4, а делитель умножить ?

Что будет если : а) и делимое и делитель умножить на 2 / 5 б) делитель разделить на 2 / 5 в) делимое умножить на 2 / 3, а делитель разделить на 2 / 3 г) делимое умножить на 7 / 4, а делитель умножить на 4 / 7 Помогите ооооочень прошу!

Частное от деления двух чисел равно 6?

Частное от деления двух чисел равно 6.

Как изменится частное если : а) делимое умножить на 4, 5, а делитель разделить на 7, 2 .

Б) делимое и делитель умножить на 0, 8.

В) делимое и делитель разделить на 5, 9 г) делимое разделить на 0, 5 , а делитель умножить на 2, 5 ?

Назовите делимое и делитель дробь обратную делителю и замените деление умножением на дробь обратную делителю в) 3 / 7делим6 / 7?

Назовите делимое и делитель дробь обратную делителю и замените деление умножением на дробь обратную делителю в) 3 / 7делим6 / 7.

Какое высказывание верно?

Какое высказывание верно?

А) Чтобы найти делимое, надо делитель умножить на частное ; б) Чтобы найти делимое, надо делитель разделить на частное ; в) Чтобы найти делимое, надо частное разделить на делитель.

Назовите делимое и делитель дробь обратную делителю и замените деление умножением на дробь обратную делителю ж) 32 / 75делим48 / 25?

Назовите делимое и делитель дробь обратную делителю и замените деление умножением на дробь обратную делителю ж) 32 / 75делим48 / 25.

Что произойдет с частным , если : а) и делимое , и делитель умножить на 2 / 5 б) делитель разделить на 2 / 5 в) делимое умножить на 2 / 3 , а делитель разделить на 2 / 3 , г) делимое умножить на 7 / 4?

Что произойдет с частным , если : а) и делимое , и делитель умножить на 2 / 5 б) делитель разделить на 2 / 5 в) делимое умножить на 2 / 3 , а делитель разделить на 2 / 3 , г) делимое умножить на 7 / 4 а делитель умножить на 4 / 7.

Как разделить делимое и делитель на одно и то же число?

Как разделить делимое и делитель на одно и то же число?

Верно ли, что если делимое и делитель — взаимно обратные числа, то частное равно 1?

Верно ли, что если делимое и делитель — взаимно обратные числа, то частное равно 1?

Назовите делимое и делитель, дробь, обратную делителю, и замените деление умножением на дробь, обратную делителю?

Назовите делимое и делитель, дробь, обратную делителю, и замените деление умножением на дробь, обратную делителю.

Вычислите полученное произведение.

Чтобы разделить одну дробь на другую надо делимое ?

Чтобы разделить одну дробь на другую надо делимое .

На этой странице находится ответ на вопрос А вот в математике 6 класса правило : чтобы разделить одну дробь на другую надо делимое умножить на число обратное делителю?, из категории Математика, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Песть в одной вазе х тюльпанов, тогда в другой, х + 6 составим уравнение : х + х + 6 = 38 2х = 38 — 6 2х = 32 х = 32 : 2 х = 16 — тюльпанов в одной вазе 16 + 6 = 22 — тюльпана в другой.

Ответ такой зарание пожалуйста 19. 1033.

1) 37 + 33 = 70% — прошел за 2 дня. 2)100 — 70 = 30% — в третий день 3) 45 : 30х100 = 150 км — весь путь. Ответ : 150 км.

37 + 33 = 70% пути за два дня 100 — 70 = 30% пути в третий день 30% = 0, 3 находим целое по его части 45 : 0, 3 = 150км всего.

3 + 8 = 11 44 : 11 = 4 — 1 часть 4 * 3 = 12 4 * 8 = 32 Эти числа : 12 и 32.

210 : 3 = 70(км / ч) — скорость автомобиля 70 + 8 = 78(км / ч) — увеличенная скорость 78 * 5 = 390(км) проедет автомобиль за 5 часов с увеличенной скоростью Ответ : 390 км.

10 кг — 100% 8 кг — х % х = 8 * 100 / 10 = 80% азота 100 — 80 = 20% кислорода.

20 чел на самолёте 20 + 35 = 55 на поезде 55 — 22 = 33 на автобусе 20 + 55 + 33 = 108 чел всего вопрос : Сколько всего было туристов? Краткую запись сам(а) сделай.

3 / 4 + 1 / 8 = 6 / 8 + 1 / 8 = 7 / 8 7 / 8 — 5 / 8 = 2 / 8 = 1 / 4.

Источник

1.2.Арифметические действия с обыкновенными дробями (Урок№2)

Умножение дроби на число

Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.

Пример 1. Умножить дробь на число 1.

Умножим числитель дроби на число 1

Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы

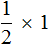
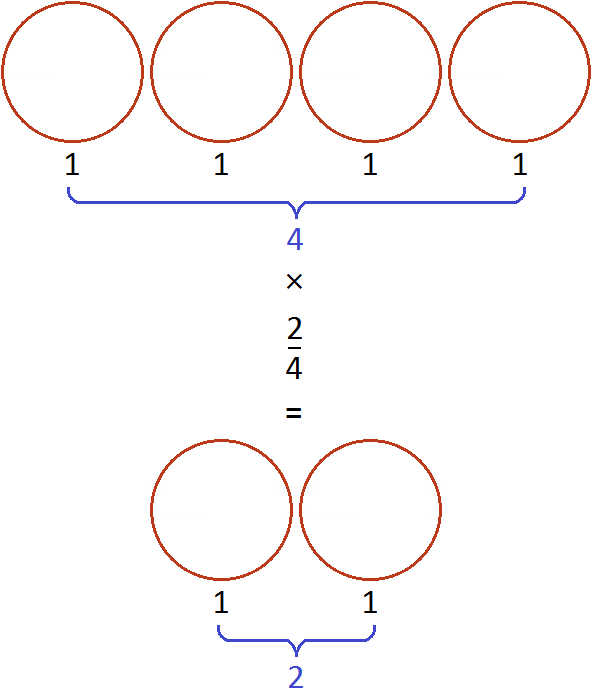
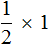
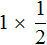
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:

Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:

Пример 2. Найти значение выражения

Умножим числитель дроби на 4

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Выражение 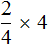можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы

А если поменять множимое и множитель местами, то получим выражение 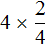. Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:

Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.

Например, выражение 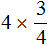можно вычислить двумя способами.

Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:

Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:

Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:

Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:

А вот к примеру выражение 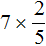можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:

Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.

Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:

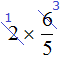
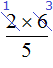
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.

Умножение дробей

Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.

Пример 1. Найти значение выражения .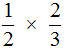

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

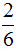
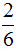
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:

Выражение 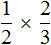можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:

У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:

Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:

Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения 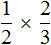равно

Пример 2. Найти значение выражения

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Пример 3. Найти значение выражения

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.

Итак, найдём НОД чисел 105 и 450:

Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15

Обратные числа

Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».

Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.

Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:

Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.

Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:

Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:

Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:

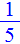
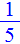
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.

Обратное число можно найти также для любого другого целого числа.

• обратным числа 2 является дробь

• обратным числа 3 является дробь

• обратным числа 4 является дробь

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.

Деление дроби на число

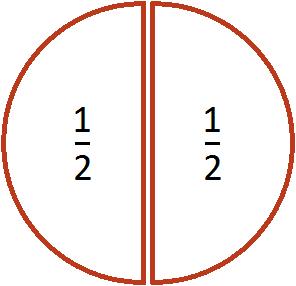
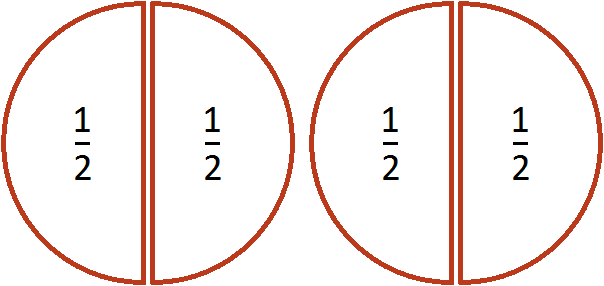
Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?

Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.

Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.

Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.

Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.

Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.

Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на

Получили ответ . Значит при делении половины на две части получается четверть.

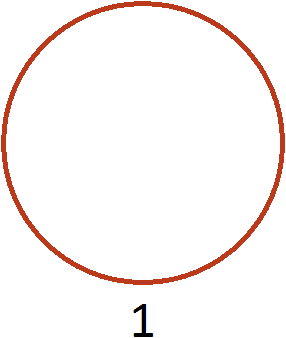
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:

Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:

Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:

Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь

В обоих случаях получился один и тот же результат.

Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь

Пример 2. Найти значение выражения

Умножим первую дробь на число, обратное делителю:

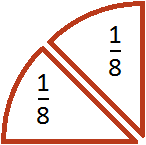
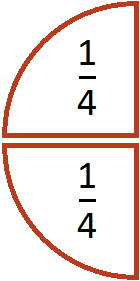
Допустим, имеется четверть пиццы и нужно разделить её на двоих:

Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:

Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5

Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь

Как видно результат не изменился. Мы снова получили ответ 5.

Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.

Пример 3. Найти значение выражения

Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь

Допустим, имелось пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков

Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается

Деление числа на дробь

Правило деления числа на дробь такое же, как и правило деления дроби на число.

Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.

Например, разделим число 1 на .

Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь

Выражение 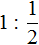можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:

Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза

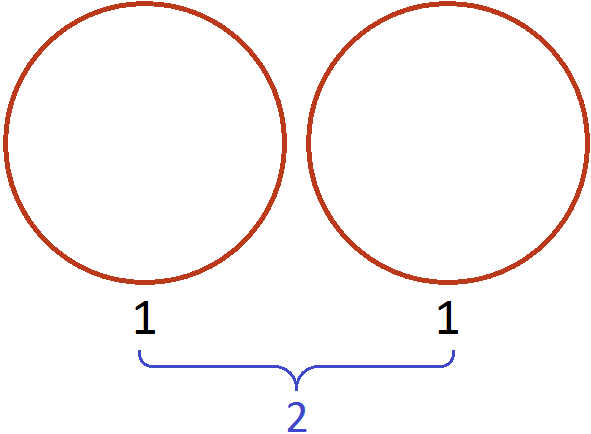
Пример 2. Найти значение выражение

Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь

Допустим, у нас имеются две целые пиццы:

Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:

Деление дробей

Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.

Например, разделим на

Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь

Допустим, имеется половина пиццы:

Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:

Пример 1. Найти значение выражения

Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:

Пример 2. Найти значение выражения

Умножаем первую дробь на дробь обратную второй:

Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.

Каждая следующая тема будет более сложной, поэтому нужно тренироваться.

Источник

Была ли эта статья полезной?

При делении чисел немаловажную услугу в смысле .прощения действия могут оказать так называемые обратные числа.
Числом, обратным данному, называется такое число, которое равно частному от деления единицы на данное число. Например, числом, обратным 4, будет или 0,25. 
Для любой обыкновенной дроби обратным числом будет та же самая дробь, но в «перевернутом» виде; например, для дроби 3/4 обратным числом будет 4/з. Вообще, чтобы найти для какого-либо числа обратное ему, достаточно разделить единицу на данное число. Полученное при этом частное и будет искомым обратным числом.

Обратные числа (меньшие единицы) для удобства вычислений с ними обычно выражаются в виде десятичных дробей.
Для чисел, больших единицы, обратные им числа выражаются десятичными дробями, содержащими столько нулей перед первой значащей цифрой, включая и нуль целых, сколько’ цифр содержит в себе целая часть данного числа. Наоборот, если данное число меньше единицы, то обратное ему число будет больше единицы, причем целая его часть будет содержать столько цифр, сколько в данном числе имеется нулей до первой значащей цифры, включая и нуль целых. Например:
Обратное число
Число
1510 151
0,00066225 0,0066225 0,066225 66,225
15,1 0,0151 0,00151
662,25
Возьмем два простейших равенства: 20:4 = 5; 20 X У4 = 5.
Из этих равенств видно, что при делении числа 20 на 4 получается тот же результат, что и при умножении делимого (20) на число (14), обратное делителю (4).
Отсюда вытекает правило: действие деления можно заменить действием умножения; для этого достаточна данное делимое умножить на число, обратное делителю.
Из всех арифметических действий, выполняемых на счетах, самым трудоемким является деление, поэтому зад мена его менее сложными приемами умножения весьма! желательна, так как это позволяет в значительной! мере экономить время и труд вычислителя. Правда, эффективность такой замены полностью обнаруживается лишь при работе на арифмометре и других механический счетных приборах, на счетах же применение этого мето да ограничено. Тем не менее, использование чисел для рационализации вычислений даже в ограниченных пределах безусловно принесет пользу.
Рассмотрим несколько примеров замены деления умножением.
Пример 1. Разделить 0,875 на 5.
Согласно вышеуказанному правилу разделить на 5 — это все равно, что умножить на число, обратное пяти. Чтобы найти это обратное число, достаточно разделить единицу на 5.
1 : 5 = 7б = 0,2.
Таким образом, задача сводится к умножению 0,875 на 0,2.
0,875:5 = 0,875 X 0,2 = 0,175.
Пример 2. Разделить 0,875 на 25.
Находим число, обратное делителю: 1 : 25 = 0,04.
Заменяем деление умножением:
0,875 X 0,04 «= 0,035.
При обычном способе деления на счетах путем вычитания для получения частного в этом примере потребовалось бы 8 раз вычесть делитель из делимого, тогда как применяя обратное число, мы сократили количество операций до 3 (при условии, конечно, что обратное число нам заранее известно)*. Выгода от замены деления умножением на обратное число становится особенно заметной при так называемом серийном делении, когда ряд чисел приходится делить на один и тот же постоянный делитель. Приведем пример такого деления.
Пример 3. Норма выработки деталей на токарном станке установлена 125 штук за смену. Фактическая выработка за первую декаду июля составила:

1.VII    120 деталей    6. VII    130 деталей
2.VII    128 »    7.VII    134 »
3.VII    127 »    8. VII    133 »
4.VII    130 »    9.VII    135 »
5.VII    135 »    10.VII    136 »
Для вычислений с обратными числами применяются специальные таблицы. Очень удобны «Таблицы обратных чисел» Н. С. Бе- лонького (М., Оргучет, “1939), в которых даны обратные значения чисел от 1 до 10 000.
Выразить ежедневную выработку в процентах к норме.
Задача окажется очень трудоемкой, если процентное отношение дневной выработки к плану определять путем деления. Например, чтобы найти процент выполнения нормы за 1 .VII, следует разделить 120 на 125, за 2.VII— 128 на 125 и т. д. за каждый день. Применяя же метод обратных чисел, мы намного сократим вычисления: найдя обратное значение постоянного делителя 125, равное 1 : 125, или 0,008, заменяем деление умножением на однозначный множитель и легко находим искомые отношения — 96%, 102,4%, 101,6% и т. д. Польза от такой замены здесь вполне очевидна.

Серийное деление — один из постоянно встречающихся видов вычислений. Всевозможные расчеты при калькуляции, распределении заработка между членами бригады, определение процентных отношений и множество подобных им вычислений немыслимы без серийного деления.
Отсюда ясно, насколько велика роль обратных чисел для рационализации вычислений.
При использовании обратных чисел следует иметь в виду, что подавляющее большинство их, будучи выражено десятичными дробями, представляет собой не точные, а приближенные значения обратных им величин. Это вполне понятно, так как частное от деления единицы на какое-либо число лишь в редких случаях может быть точно выражено десятичной дробью (точными значениями являются, например, числа 0,2, 0,4, 0,5, обратные числам 5, 2,5, 2 и т. п.). Зато, с другой стороны, приближенные значения обратных чисел могут быть как угодно близки к точным значениям, поэтому погрешность при вычислениях с ними можно доводить до нич-тожных размеров.
Каждый, кому в повседневных вычислениях приходится иметь дело с ограниченным количеством постоянных делителей, легко может рационализировать работу, составив для них таблицу обратных чисел.
Упражнение 46. Найти обратные значения для чисел
а) 125; 1,25; 0,0125; 12 500;
б) 375; 37,5; 0,000375 (с точностью до 4-го знака).

Добавить комментарий

Авторизоваться

Рекомендуемые статьи

Scroll to top

Обратное число

Обра́тное число́ (обратное значение, обратная величина) — это число, на которое надо умножить данное число, чтобы получить единицу. Пара чисел, произведение которых равно единице, называются взаимно обратными.

Примеры: 5 и 1/5, −6/7 и −7/6, и

Для всякого числа а, не равного нулю, существует обратное 1/a.

Обратной величиной нуля является бесконечность.

Обратные дроби — это две дроби, произведение которых равно 1. Например, 3/7 и 7/3; 5/8 и 8/5 и т. д.

См. также

• Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).
• Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.

Wikimedia Foundation . 2010 .

Смотреть что такое «Обратное число» в других словарях:

ОБРАТНОЕ ЧИСЛО — число, произведение которого на данное число равно единице. Два таких числа называются взаимно обратными. Таковы, напр., 5 и 1/5, 2/3 и 3/2 и т. д … Большой Энциклопедический словарь

обратное число — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN inverse numberreciprocal number … Справочник технического переводчика

обратное число — число, произведение которого на данное число равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 и 1/5, 2/3 и 3/2 и т. д. * * * ОБРАТНОЕ ЧИСЛО ОБРАТНОЕ ЧИСЛО, число, произведение которого на данное число равно… … Энциклопедический словарь

Обратное число — число, произведение которого с данным числом равно единице. Два таких числа называются взаимно обратными. Таковы, например, 5 и а, не равного нулю, существует обратное … Большая советская энциклопедия

ОБРАТНОЕ ЧИСЛО — число, произведение к рого на данное число равно единице. Два таких числа наз. взаимно обратными. Таковы, напр., 5 и 1/5. 2/3 и 3/2 и т. д … Естествознание. Энциклопедический словарь

Число — У этого термина существуют и другие значения, см. Число (значения). Число  основное понятие математики[1], используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей… … Википедия

Число (матем.) — см. также: Число (лингвистика) Число абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое … Википедия

Обратное закручивание воды при стоке — Обратное закручивание воды при стоке  околонаучный миф, основанный на неверном применении эффекта Кориолиса к движению воды в водовороте, возникающему при её стоке в сливное отверстие раковины или ванны. Суть мифа состоит в том, что вода… … Википедия

ЧИСЛО ИРРАЦИОНАЛЬНОЕ — ЧИСЛО, ИРРАЦИОНАЛЬНОЕ, число, которое не может быть выражено в виде дроби. Примеры включают Ц2 и число p. Следовательно, иррациональные числа это числа с бесконечным числом (непериодических) знаков после запятой. (Однако обратное не является… … Научно-технический энциклопедический словарь

Обратное преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия

Источник

ОБРАТНЫЕ ЧИСЛА И ПРИМЕНЕНИЕ ИХ ПРИ ДЕЛЕНИИ

При делении чисел немаловажную услугу в смысле .прощения действия могут оказать так называемые обратные числа.
Числом, обратным данному, называется такое число, которое равно частному от деления единицы на данное число. Например, числом, обратным 4, будет или 0,25.
Для любой обыкновенной дроби обратным числом будет та же самая дробь, но в «перевернутом» виде; например, для дроби 3/4 обратным числом будет 4/з. Вообще, чтобы найти для какого-либо числа обратное ему, достаточно разделить единицу на данное число. Полученное при этом частное и будет искомым обратным числом.

Обратные числа (меньшие единицы) для удобства вычислений с ними обычно выражаются в виде десятичных дробей.
Для чисел, больших единицы, обратные им числа выражаются десятичными дробями, содержащими столько нулей перед первой значащей цифрой, включая и нуль целых, сколько’ цифр содержит в себе целая часть данного числа. Наоборот, если данное число меньше единицы, то обратное ему число будет больше единицы, причем целая его часть будет содержать столько цифр, сколько в данном числе имеется нулей до первой значащей цифры, включая и нуль целых. Например:
Обратное число
Число
1510 151
0,00066225 0,0066225 0,066225 66,225
15,1 0,0151 0,00151
662,25
Возьмем два простейших равенства: 20:4 = 5; 20 X У4 = 5.
Из этих равенств видно, что при делении числа 20 на 4 получается тот же результат, что и при умножении делимого (20) на число (14), обратное делителю (4).
Отсюда вытекает правило: действие деления можно заменить действием умножения; для этого достаточна данное делимое умножить на число, обратное делителю.
Из всех арифметических действий, выполняемых на счетах, самым трудоемким является деление, поэтому зад мена его менее сложными приемами умножения весьма! желательна, так как это позволяет в значительной! мере экономить время и труд вычислителя. Правда, эффективность такой замены полностью обнаруживается лишь при работе на арифмометре и других механический счетных приборах, на счетах же применение этого мето да ограничено. Тем не менее, использование чисел для рационализации вычислений даже в ограниченных пределах безусловно принесет пользу.
Рассмотрим несколько примеров замены деления умножением.
Пример 1. Разделить 0,875 на 5.
Согласно вышеуказанному правилу разделить на 5 — это все равно, что умножить на число, обратное пяти. Чтобы найти это обратное число, достаточно разделить единицу на 5.
1 : 5 = 7б = 0,2.
Таким образом, задача сводится к умножению 0,875 на 0,2.
0,875:5 = 0,875 X 0,2 = 0,175.
Пример 2. Разделить 0,875 на 25.
Находим число, обратное делителю: 1 : 25 = 0,04.
Заменяем деление умножением:
0,875 X 0,04 «= 0,035.
При обычном способе деления на счетах путем вычитания для получения частного в этом примере потребовалось бы 8 раз вычесть делитель из делимого, тогда как применяя обратное число, мы сократили количество операций до 3 (при условии, конечно, что обратное число нам заранее известно)*. Выгода от замены деления умножением на обратное число становится особенно заметной при так называемом серийном делении, когда ряд чисел приходится делить на один и тот же постоянный делитель. Приведем пример такого деления.
Пример 3. Норма выработки деталей на токарном станке установлена 125 штук за смену. Фактическая выработка за первую декаду июля составила:
1.VII 120 деталей 6. VII 130 деталей
2.VII 128 » 7.VII 134 »
3.VII 127 » 8. VII 133 »
4.VII 130 » 9.VII 135 »
5.VII 135 » 10.VII 136 »
Для вычислений с обратными числами применяются специальные таблицы. Очень удобны «Таблицы обратных чисел» Н. С. Бе- лонького (М., Оргучет, «1939), в которых даны обратные значения чисел от 1 до 10 000.
Выразить ежедневную выработку в процентах к норме.
Задача окажется очень трудоемкой, если процентное отношение дневной выработки к плану определять путем деления. Например, чтобы найти процент выполнения нормы за 1 .VII, следует разделить 120 на 125, за 2.VII— 128 на 125 и т. д. за каждый день. Применяя же метод обратных чисел, мы намного сократим вычисления: найдя обратное значение постоянного делителя 125, равное 1 : 125, или 0,008, заменяем деление умножением на однозначный множитель и легко находим искомые отношения — 96%, 102,4%, 101,6% и т. д. Польза от такой замены здесь вполне очевидна.

Источник

Взаимно обратные числа, нахождение обратного числа.

Дадим определение и приведем примеры взаимно обратных чисел. Рассмотрим, как находить число, обратное натуральному числу и обратное обыкновенной дроби. Помимо этого, запишем и докажем неравенство, отражающее свойство суммы взаимно обратных чисел.

Взаимно обратные числа. Определение

Взаимно обратные числа — такие числа, произведение которых дает единицу.

Если a · b = 1 , то можно сказать, что число a обратно числу b , так же как и число b обратно числу a .

Самый простой пример взаимно обратных чисел — две единицы. Действительно, 1 · 1 = 1 , поэтому a = 1 и b = 1 — взаимно обратные числа. Другой пример — числа 3 и 1 3 , — 2 3 и — 3 2 , 6 13 и 13 6 , log 3 17 и log 17 3 . Произведение любой пары указанных выше чисел равно единице. Если это условие не выполняется, как например у чисел 2 и 2 3 , то числа не являются взаимно обратными.

Определение взаимно обратных чисел справедливо для любый чисел — натуральных, целых, действительных и комплексных.

Как найти число, обратное данному

Рассмотрим общий случай. Если исходное число равно a , то обратное ему число запишется в виде 1 a , или a — 1 . Действительно, a · 1 a = a · a — 1 = 1 .

Для натуральных чисел и обыкновенных дробей найти обратное число довольно просто. Можно сказать, даже очевидно. В случае нахождения числа, обратного иррациональному или комплексному числу, придется произвести ряд вычислений.

Рассмотрим наиболее часто встречающиеся на практике случаи нахождения обратного числа.

Число, обратное обыкновенной дроби

Очевидно, что число, обратное обыкновенной дроби a b — это дробь b a . Итак, чтобы найти обратное дроби число, дробь нужно просто перевернуть. То есть, поменять числитель и знаменатель местами.

Согласно этому правилу, записать обратное любой обыкновенной дроби число можно практически сразу. Так, для дроби 28 57 обратным числом будет дробь 57 28 , а для дроби 789 256 — число 256 789 .

Число, обратное натуральному числу

Найти число, обратное любому натуральному числу, можно так же, как и число, обратное дроби. Достаточно представить натуральное число a в виде обыкновенной дроби a 1 . Тогда обратным ему числом будет число 1 a . Для натурального числа 3 обратным ему числом будет дробь 1 3 , для числа 666 обратное число равно 1 666 , и так далее.

Отдельное внимание стоит уделить единице, так как это единственное число, обратное число для которого равно ему самому.

Других пар взаимно обратных чисел, где обе составляющие равны, не существует.

Число, обратное смешанному числу

Смешанное число имеем вид a b c . Чтобы найти обратное ему число, необходимо смешанное число представить в сиде неправильной дроби, и уже для полученной дроби подобрать обратное число.

Например, найдем обратное число для 7 2 5 . Сначала представим 7 2 5 в виде неправильной дроби: 7 2 5 = 7 · 5 + 2 5 = 37 5 .

Для неправильной дроби 37 5 обратным числом будет дробь 5 37 .

Число, обратное десятичной дроби

Десятичная дробь также можно представить в виде обыкновенной дроби. Нахождение обратного десятичной дроби числа сводится к представлению десятичной дроби в виде обыкновенной дроби и нахождению обратного числа для нее.

Например, есть дробь 5 , 128 . Найдем обратное ей число. Сначала переводим десятичную дробь в обыкновенную: 5 , 128 = 5 128 1000 = 5 32 250 = 5 16 125 = 641 125 . Для полученной дроби обратным числом будет дробь 125 641 .

Рассмотрим еще один пример.

Пример. Нахождение числа, обратного десятичной дроби

Найдем обратное число для периодической десятичной дроби 2 , ( 18 ) .

Переводим десятичную дробь в обыкновенную:

2 , 18 = 2 + 18 · 10 — 2 + 18 · 10 — 4 + . . . = 2 + 18 · 10 — 2 1 — 10 — 2 = 2 + 18 99 = 2 + 2 11 = 24 11

После перевода можем легко записать обратное число для дроби 24 11 . Этим числом, очевидно, будет 11 24 .

Для бесконечной и непериодической десятичной дроби обратное число записывается в виде дроби и единицей в числителе и самой дробью в знаменателе. Например, для бесконечной дроби 3 , 6025635789 . . . обратное число будет иметь вид 1 3 , 6025635789 . . . .

Аналогично и для иррациональных чисел, отвечающим непериодическим бесконечным дробям, обратные числа записываются в виде дробных выражений.

К примеру, обратным числом для π + 3 3 80 будет 80 π + 3 3 , а для числа 8 + е 2 + е обратным числом будет дробь 1 8 + е 2 + е .

Взаимно обратные числа с корнями

Если вид двух чисел отличен от a и 1 a , то не всегда можно легко определить, являются ли числа взаимно обратными. Это особенно актуально для чисел, которые имеют в своей записи знак корня, так как от корня обычно принято избавляться в знаменателе.

Обратимся к практике.

Пример. Взаимно обратные числа с корнями

Ответим на вопрос: являются ли взаимно обратными числа 4 — 2 3 и 1 + 3 2 .

Чтобы узнать, являются ли числа взаимно обратными, вычислим их произведение.

4 — 2 3 · 1 + 3 2 = 4 — 2 3 + 2 3 — 3 = 1

Произведение равно единице, значит, числа взаимно обратны.

Рассмотрим еще один пример.

Пример. Взаимно обратные числа с корнями

Запишите число, обратное числу 5 3 + 1 .

Сразу можно записать, что обратное число равно дроби 1 5 3 + 1 . Однако, как мы уже говорили, принято избавляться от корня в знаменателе. Чтобы сделать это умножим числитель и знаменатель на 25 3 — 5 3 + 1 . Получим:

1 5 3 + 1 = 25 3 — 5 3 + 1 5 3 + 1 · 25 3 — 5 3 + 1 = 25 3 — 5 3 + 1 5 3 3 + 1 3 = 25 3 — 5 3 + 1 6

Взаимно обратные числа со степенями

Допустим, есть число, равное какой-то степени числа a . Другими словами, число a , возведенное в степень n . Обратным числу a n будет число a — n . Проверим это. Действительно: a n · a — n = a n 1 · 1 a n = 1 .

Пример. Взаимно обратные числа со степенями

Найдем обратное число для 5 — 3 + 4 .

Согласно написанному выше, искомое число равно 5 — — 3 + 4 = 5 3 — 4

Взаимно обратные числа с логарифмами

Для логарифма числа a по основанию b обратным является число, равное логарифму числа b по основанию a .

log a b и log b a — взаимно обратные числа.

Проверим это. Из свойств логарифма следует, что log a b = 1 log b a , значит log a b · log b a .

Пример. Взаимно обратные числа с логарифмами

Найти число, обратное log 3 5 — 2 3 .

Числом, обратным логарифму числа 3 по основанию 3 5 — 2 будет логарифм числа 3 5 — 2 по основанию 3 .

Число, обратное комплексному числу

Как уже отмечалось ранее, определение взаимно обратных чисел справедливо не только для действительных чисел, но и для комплексных.

Обычно комплексные числа представляют в алгебраическом виде z = x + i y . Числом, обратным данному, будет дробь

1 x + i y . Для удобства можно сократить это выражение, умножив числитель и знаменатель на x — i y .

Пример. Число, обратное комплексному числу

Пусть есть комплексное число z = 4 + i . Найдем число, обратное ему.

Число, обратное z = 4 + i , будет равно 1 4 + i .

Умножим числитель и знаменатель на 4 — i и получим:

1 4 + i = 4 — i 4 + i 4 — i = 4 — i 4 2 — i 2 = 4 — i 16 — ( — 1 ) = 4 — i 17 .

Помимо алгебраической формы, комплексное число может быть представлено в тригонометрической или показательной форме следующим образом:

z = r · cos φ + i · sin φ

Соответственно, обратное число будет иметь вид:

1 r cos ( — φ ) + i · sin ( — φ )

Убедимся в этом:

r · cos φ + i · sin φ · 1 r cos ( — φ ) + i · sin ( — φ ) = r r cos 2 φ + sin 2 φ = 1 r · e i · φ · 1 r e i · ( — φ ) = r r e 0 = 1

Рассмотрим примеры с представлением комплексных чисел в тригонометрической и показательной форме.

Пример. Найти число, обратное комплексному числу

Найдем число, обратное для 2 3 cos π 6 + i · sin π 6 .

Учитывая, что r = 2 3 , φ = π 6 , запишем обратное число

3 2 cos — π 6 + i · sin — π 6

Какое число будет обратным для 2 · e i · — 2 π 5 .

Ответ: 1 2 · e i 2 π 5

Сумма взаимно обратных чисел. Неравенство

Существует теорема о сумме двух взаимно обратных чисел.

Сумма взаимно обратных чисел

Сумма двух положительных и взаимно обратных чисел всегда больше или равна 2 .

Приведем доказательство теоремы. Как известно, для любых положительных чисел a и b среднее арифметическое больше или равно среднему геометрическому. Это можно записать в виде неравенства:

Источник

Обратные числа

Например: числа (5) и (0,2) – взаимообратные, так как (5·0,2=1).

Обратным для числа (a) будет число (frac<1>)

число обратное (3):

число обратное (5):

Если число представляет собой дробь, то обратным ему будет «перевернутая» дробь.

число обратное (frac<3><7>) :

Пример: Запишите число, обратное числу (1,2).

Решение: Число (1,2) представляет собой десятичную дробь , и значит, может быть превращено в дробь обыкновенную : (1,2=) (frac<12><10>) (=) (frac<6><5>) . Отсюда получаем, что обратное число будет: (frac<5><6>) .
Проверка: (1,2cdot) (frac<5><6>) (=) (frac<1,2cdot5><6>) (=) (frac<6><6>) (=1).

Отметим, что обратного числа для (0) не существует, потому что (frac<1><0>) – не вычисляется (на ноль делить нельзя).

Если исходное число отрицательно, то и обратное ему также будет отрицательным, потому что иначе при их перемножении получится не (1), а (-1).

Пример: Запишите число, обратное числу (-1) (frac<2><3>) .

Решение: Число (-1) (frac<2><3>) — является смешанной дробью, превращаем в обыкновенную: (-1) (frac<2><3>) (=-) (frac<5><3>) . На какое число надо умножать эту дробь, чтоб получилось (1)? На (-) (frac<3><5>) . Это и есть ответ.

Не путайте обратные числа с противоположными . Напомним, что противоположные – это числа одинаковым значением, но разным знаком, например, (2) и (-2) или (7) и (-7).

Источник

Обратные числа

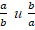
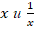
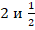
Обратными – или взаимно-обратными – числами называют пару чисел, которые при перемножении дают 1. В самом общем виде обратными являются числа . Характерный частный случай взаимно-обратных чисел – пара . Обратными являются, скажем, числа ; .

Как найти обратное число

Правило: нужно 1 (единицу) поделить на данное число.

Дано число 8. Обратное к нему – 1:8 или (второй вариант предпочтительнее, потому что такая запись математически более корректна).

Когда ищется обратное число для обыкновенной дроби, то делить ее на 1 не очень удобно, т.к. запись получается громоздкой. В этом случае гораздо проще поступать иначе: дробь просто переворачивают, меняя местами числитель и знаменатель. Если дана правильная дробь, то после переворачивания получается дробь неправильная, т.е. такая, из которой можно выделить целую часть. Делать это или нет, решать нужно в каждом конкретном случае особо. Так, если с полученной перевернутой дробью далее придется совершать какие-то действия (к примеру, умножение или деление), то выделять целую часть не стоит. Если же полученная дробь – это конечный результат, то, возможно, выделение целой части и желательно.

Дана дробь . Обратная к ней: .

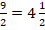
Если требуется найти обратное число к десятичной дроби, то следует воспользоваться первым правилом (деление 1 на число). В этой ситуации можно действовать одним из 2 способов. Первый – просто разделить 1 на это число в столбик. Второй – сформировать дробь из 1 в числителе и десятичной дроби в знаменателе, а затем домножить числитель и знаменатель на 10, 100 или другое число, состоящее из 1 и такого количества нулей, которое необходимо, чтобы избавиться от десятичной запятой в знаменателе. В результате будет получена обыкновенная дробь, которая и является результатом. При необходимости ее может понадобиться сократить, выделить из нее целую часть или перевести в десятичный вид.

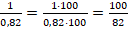
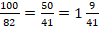
Дано число 0,82. Обратное число к нему такое: . Теперь сократим дробь и выделим целую часть: .

Как проверить, являются ли два числа обратными

Принцип проверки основан на определении обратных чисел. То есть для того, чтобы убедиться, что числа являются обратными друг другу, нужно перемножить их. Если в результате будет получена единица, значит, числа – взаимно обратные.

Даны числа 0,125 и 8. Являются ли они обратными?

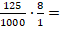
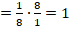
Проверка. Необходимо найти произведение 0,125 и 8. Для наглядности представим данные числа в виде обыкновенных дробей: (сократим 1-ю дробь на 125) . Вывод: числа 0,125 и 8 являются обратными.

Свойства обратных чисел

Свойство №1

Обратное число существует для любого числа, кроме 0.

Это ограничение связано с тем, что нельзя делить на 0, а при определении обратного числа для нуля его как раз придется переместить в знаменатель, т.е. фактически делить на него.

Свойство №2

Математически это свойство можно выразить неравенством: .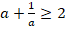

Свойство №3

Умножение числа на два взаимно-обратных числа равносильно умножению на единицу. Выразим это свойство математически: .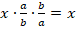

Найти значение выражения: 3,4·0,125·8. Поскольку числа 0,125 и 8 являются обратными (см. Пример №4), то умножать 3,4 на 0,125 и затем на 8 нет необходимости. А значит, ответом здесь будет 3,4.

Свойство №4

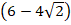
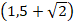
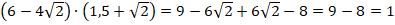
Выражения и являются обратными. Докажем это: .

Свойство №5

Для числа, представленного в виде степени с показателем х, обратным будет число в виде степени с показателем –х. Обоснование: 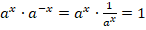. Это свойство означает, что и для всякой степени тоже может быть подобрано обратное число.

Дано число 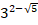. Требуется найти обратное к нему.

Решение. Обратное число в данном случае равно: .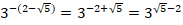

Источник

ГДЗ и решебники
вип уровня