Как найди период полураспада - Сайт, где вы сможете решить свои вопросы

Ядерная физика

Атомное ядро · Радиоактивный распад · Ядерная реакция · Термоядерная реакция
Основные термины Атомное ядро · Изотопы · Изобары · Капельная модель ядра · Период полураспада · Массовое число · Составное ядро · Цепная ядерная реакция · Ядерное эффективное сечение
Распад ядер Закон радиоактивного распада · Альфа-распад · Бета-распад · Кластерный распад
Сложный распад Электронный захват · Двойной бета-распад · Двойной электронный захват · Внутренняя конверсия · Изомерный переход
Излучения Ионизирующее излучение · Нейтронный распад · Позитронный распад · Протонный распад · Гамма излучение · Фоторасщепление
Захваты Электронный захват · Нейтронный захват (r-процесс · s-процесс) · Протонный захват (p-процесс · rp-процесс) · Нейтронизация
Деление ядра Спонтанное деление
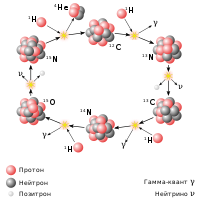
Нуклеосинтез Первичный нуклеосинтез · Протон-протонный цикл · CNO-цикл · Тройная гелиевая реакция · Гелиевая вспышка · Ядерное горение углерода · Углеродная детонация · Ядерное горение кислорода · Ядерное горение неона · Ядерное горение кремния · Реакции скалывания
См. также: Портал:Физика

Пери́од полураспа́да квантовомеханической системы (частицы, ядра, атома, энергетического уровня и т. д.) — время $T_{{1/2}}$ , в течение которого система распадается с вероятностью 1/2^[1]. В течение одного периода полураспада в среднем вдвое уменьшается количество выживших частиц^[1]^[2]^[3]^[4]^[5]^[6], а также интенсивность реакции распада^[2]^[5]^[6].

Период полураспада наглядно характеризует скорость распада радиоактивных ядер, наряду со средним временем жизни и вероятностью распада в единицу времени (постоянной распада), эти величины связаны друг с другом простым однозначным соотношением^[2]^[3]^[4]^[5]^[6].

Период полураспада является константой для данного радиоактивного ядра (изотопа). Для различных изотопов эта величина может изменяться от десятков йоктосекунд (10⁻²⁴ с) у водорода-7 до более чем 10²⁴ лет у теллура-128, что многократно превышает возраст Вселенной^[4]^[5]. На основании постоянства периода полураспада строится метод радиоизотопного датирования^[5].

Определение и основные соотношения[править | править код]

Понятие периода полураспада применяется как к испытывающим распад элементарным частицам, так и к радиоактивным ядрам^[4]. Поскольку событие распада имеет квантовую вероятностную природу, то если рассматривать одну структурную единицу материи (частицу, атом радиоактивного изотопа), можно говорить о периоде полураспада как промежутке времени, по истечении которого средняя вероятность распада рассматриваемой частицы будет равна 1/2^[1].

Если же рассматривать экспоненциально распадающиеся системы частиц, то периодом полураспада $T_{{1/2}}$ будет называться время, в течение которого распадается в среднем половина радиоактивных ядер^[1]^[2]^[3]^[4]^[5]^[6]. Согласно закону радиоактивного распада, число нераспавшихся атомов в момент времени связано с начальным (в момент t = 0 ) числом атомов $N_{0}$ соотношением

${displaystyle {frac {N(t)}{N_{0}}}=e^{-lambda t},}$

где

— постоянная распада^[7].

По определению, ${displaystyle {frac {N(T_{1/2})}{N_{0}}}={frac {1}{2}},}$ следовательно, ${displaystyle e^{-lambda T_{1/2}}={frac {1}{2}},}$ откуда

${displaystyle T_{1/2}={frac {ln 2}{lambda }}approx {frac {0,693}{lambda }}.}$

Далее, поскольку среднее время жизни ${displaystyle tau ={frac {1}{lambda }}}$ , то^[2]^[3]^[4]^[5]^[6]

${displaystyle T_{1/2}=tau ln 2approx 0,693tau ,}$

то есть период полураспада примерно на 30,7 % короче, чем среднее время жизни. Например, для свободного нейтрона $T_{{1/2}}$ = 10,3 минуты, а tau = 14,9 минуты^[5].

Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время ${displaystyle 2T_{1/2}}$ останется четверть от начального числа частиц, за ${displaystyle 3T_{1/2}}$ — одна восьмая и т. д.^[1]^[5]. При этом для каждой конкретной отдельной частицы по прошествии времени $T_{{1/2}}$ ожидаемая средняя продолжительность жизни (соответственно, и вероятность распада, и период полураспада) не изменится — этот контринтуитивный факт является следствием квантовой природы явления распада^[1].

Парциальный период полураспада[править | править код]

Если система с периодом полураспада $T_{{1/2}}$ может распадаться по нескольким каналам, для каждого из них можно определить парциальный период полураспада. Пусть вероятность распада по i-му каналу (коэффициент ветвления) равна $p_{i}$ . Тогда парциальный период полураспада по i-му каналу равен

${displaystyle T_{1/2}^{(i)}={frac {T_{1/2}}{p_{i}}}.}$

Парциальный $T_{{1/2}}^{{(i)}}$ имеет смысл периода полураспада, который был бы у данной системы, если «выключить» все каналы распада, кроме i-го. Так как по определению $p_{i}leq 1$ , то $T_{{1/2}}^{{(i)}}geq T_{{1/2}}$ для любого канала распада.

Значения для различных изотопов[править | править код]

Период полураспада конкретного изотопа является постоянной величиной, не зависящей от способа его получения, агрегатного состояния вещества, температуры, давления, химического состава соединения, куда оно входит, и практически любых других внешних факторов, за исключением акта прямого ядерного взаимодействия в результате, например, соударения с высокоэнергетической частицей в ускорителе^[5]^[6].

На практике период полураспада определяют, измеряя активность исследуемого препарата через определённые промежутки времени. Учитывая, что активность препарата пропорциональна количеству атомов распадающегося вещества, и воспользовавшись законом радиоактивного распада, можно вычислить период полураспада данного вещества^[8].

Значения периода полураспада для различных радиоактивных изотопов:

Химический элемент	Обозначение	Порядковый номер (Z)	Массовое число (A)	Период полураспада
Актиний	Ac	89	227	22 года^[9]^[10]
Америций	Am	95	243	7,3⋅10³ лет^[10]^[11]
Астат	At	85	210	8,3 часа^[9]
Бериллий	Be	4	8	8,2⋅10^-17 секунды^[11]
Висмут	Bi	83	208	3,68⋅10⁵ лет^[11]^[12]
209	2⋅10¹⁹ лет^[10]^[13]
210	3,04⋅10⁶ лет^[12]^[13]
Берклий	Bk	97	247	1,38⋅10³ лет^[10]^[11]
Углерод	C	6	14	5730 лет^[1]^[13]
Кадмий	Cd	48	113	9⋅10¹⁵ лет^[14]
Хлор	Cl	17	36	3⋅10⁵ лет^[13]
38	38 минут^[13]
Кюрий	Cm	96	247	4⋅10⁷ лет^[9]
Кобальт	Co	27	60	5,27 года^[13]^[15]
Цезий	Cs	55	137	30,1 года^[1]^[15]
Эйнштейний	Es	99	254	1,3 года^[9]^[10]
Фтор	F	9	18	110 минут^[11]^[15]
Железо	Fe	26	59	45 дней^[1]^[13]
Франций	Fr	87	223	22 минуты^[9]^[10]
Галлий	Ga	31	68	68 минут^[11]
Водород	H	1	3	12,3 года^[13]^[15]
Йод	I	53	131	8 дней^[13]^[15]
Иридий	Ir	77	192	74 дня^[13]
Калий	K	19	40	1,25⋅10⁹ лет^[1]^[11]
Молибден	Mo	42	99	66 часов^[5]^[11]
Азот	N	7	13	10 минут^[13]
Натрий	Na	11	22	2,6 года^[13]^[15]
24	15 часов^[1]^[13]^[15]
Нептуний	Np	93	237	2,1⋅10⁶ лет^[10]^[11]
Кислород	O	8	15	124 секунды^[13]
Фосфор	P	15	32	14,3 дня^[1]^[13]
Протактиний	Pa	91	231	3,3⋅10⁴ лет^[11]^[13]
Полоний	Po	84	210	138,4 дня^[9]^[13]
214	0,16 секунды^[11]
Плутоний	Pu	94	238	87,7 года^[11]
239	2,44⋅10⁴ лет^[1]^[13]
242	3,3⋅10⁵ лет^[9]
Радий	Ra	88	226	1,6⋅10³ лет^[9]^[11]^[10]
Рубидий	Rb	37	82	76 секунд^[11]
87	49,7⋅10⁹ лет^[11]
Радон	Rn	86	222	3,83 дня^[9]^[13]
Сера	S	16	35	87 дней^[13]
Самарий	Sm	62	147	1,07⋅10¹¹ лет^[11]^[12]
148	6,3⋅10¹⁵ лет^[11]
149	> 2⋅10¹⁵ лет^[11]^[12]
Стронций	Sr	38	89	50,5 дня^[13]
90	28,8 года^[11]
Технеций	Tc	43	99	2,1⋅10⁵ лет^[9]^[10]
Теллур	Te	52	128	2⋅10²⁴ лет^[11]
Торий	Th	90	232	1,4⋅10¹⁰ лет^[9]^[10]
Уран	U	92	233	1,⋅10⁵ лет^[13]
234	2,5⋅10⁵ лет^[13]
235	7,1⋅10⁸ лет^[1]^[13]
238	4,5⋅10⁹ лет^[1]^[9]^[10]^[13]
Ксенон	Xe	54	133	5,3 дня^[13]^[15]
Иттрий	Y	39	90	64 часа^[13]

Примеры расчётов[править | править код]

Пример 1[править | править код]

Если рассматривать достаточно близкие моменты времени $t_{1}$ и $t_{2}$ , то число ядер, распавшихся за этот промежуток времени ${displaystyle t_{2}-t_{1}ll lambda }$ , можно приближённо записать как ${displaystyle Delta Napprox lambda N_{0}(t_{2}-t_{1})}$ .

С её помощью легко оценить число атомов урана-238, имеющего период полураспада ${displaystyle T_{1/2}=4,498cdot 10^{9}}$ лет, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Имея в виду, что количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02⋅10²³ атомов, а в году секунд, можно получить, что

${displaystyle Delta Napprox {frac {0,693}{4,498cdot 10^{9}cdot 365cdot 24cdot 60cdot 60}}{frac {6,02cdot 10^{23}}{238}}cdot 1000=12cdot 10^{6}.}$

Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду из наличного количества урана распадается его доля, равная

${displaystyle {frac {12cdot 10^{6}cdot 238}{6,02cdot 10^{23}cdot 1000}}=47cdot 10^{-19}.}$

Пример 2[править | править код]

Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?

Поскольку рассматриваемое время (1 с) намного меньше периода полураспада, можно применить ту же, что и в предыдущем примере, приближённую формулу:

${displaystyle Delta Napprox Delta tcdot N_{0}{frac {ln 2}{T_{1/2}}}=Delta tcdot {frac {{frac {m}{mu }}N_{A}ln 2}{T_{1/2}}}}$

Подстановка численных значений даёт
${displaystyle Delta Napprox 1cdot {frac {0,693cdot {frac {10}{239}}cdot 6cdot 10^{23}}{24400cdot 365cdot 24cdot 60cdot 60}}={frac {0,693cdot 2,5cdot 10^{22}}{7,7cdot 10^{11}}}=2,25cdot 10^{10}.}$

Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться точной формулой

$Delta N=N_{0}-N(t)=N_{0}left(1-2^{{-t/T_{{1/2}}}}right).$

Она пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Так, для данной задачи:

$Delta N=N_{0}left(1-2^{{-t/T_{{1/2}}}}right)=2.5cdot 10^{{22}}left(1-2^{{-1/7.7cdot 10^{{11}}}}right)=2.5cdot 10^{{22}}left(1-0.99999999999910right)=2.25cdot 10^{{10}}.$

Стабильность периода полураспада[править | править код]

Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков: зная концентрацию радиоизотопа в настоящее время и в прошлом, можно рассчитать, сколько точно времени прошло с тех пор^[5].

Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).

Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.

Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %^[16]; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.

См. также[править | править код]

Время жизни квантовомеханической системы
Ширина распада

Примечания[править | править код]

↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ Richard A. Muller. Physics and Technology for Future Presidents : An Introduction to the Essential Physics Every World Leader Needs to Know : [англ.]. — Princeton, New Jercey : Princeton University Press, 2010. — С. 128—129. — 526 с. — ISBN 978-0-691-13504-5.
↑ ¹ ² ³ ⁴ ⁵ Климов А. Н. Глава 3. Ядерные превращения // Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 74—75. — 352 с.
↑ ¹ ² ³ ⁴ Период полураспада. Энциклопедия физики и техники. Дата обращения: 18 ноября 2019. Архивировано 4 декабря 2019 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ Б.С. Ишханов, И.М. Капитонов, Э.И. Кэбин. Период полураспада. Частицы и атомные ядра. Основные понятия. Кафедра общей ядерной физики физического факультета МГУ. Дата обращения: 18 ноября 2019. Архивировано 6 ноября 2019 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² Carl R. (Rod) Nave. Radioactive Half-Life. HyperPhysics. Georgia State University (2016). Дата обращения: 22 ноября 2019. Архивировано 27 сентября 2017 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ Б.С. Ишханов, И.М. Капитонов, Н.П. Юдин. Радиоактивность // Частицы и атомные ядра. — 2-е. — М. : Издательство ЛКИ. — Гл. 1. Элементарные частицы. — С. 18—21. — 584 с. — (Классический университетский учебник). — ISBN 978-5-382-00060-2.
↑ Такой же вид имеет зависимость от времени интенсивности (скорости) распада, то есть активности образца, и аналогичным образом через неё определяется период полураспада как промежуток времени, по истечении которого интенсивность распада снизится вдвое
↑ Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² Период полураспада радиоактивных элементов и их излучение (Таблица). infotables.ru – Справочные таблицы. Дата обращения: 6 ноября 2019. Архивировано 6 ноября 2019 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ Half Life for all the elements in the Periodic Table. periodictable.com. Дата обращения: 11 ноября 2019. Архивировано 24 марта 2019 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ ¹⁷ ¹⁸ ¹⁹ ²⁰ Kondev F. G., Wang M., Huang W. J., Naimi S., Audi G. The Nubase2020 evaluation of nuclear properties (англ.) // Chinese Physics C. — 2021. — Vol. 45, iss. 3. — P. 030001-1—030001-180. — doi:10.1088/1674-1137/abddae.
↑ ¹ ² ³ ⁴ Radioactive isotope table. Caltech Astronomy Department. Дата обращения: 10 ноября 2019. Архивировано 31 октября 2019 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ¹⁰ ¹¹ ¹² ¹³ ¹⁴ ¹⁵ ¹⁶ ¹⁷ ¹⁸ ¹⁹ ²⁰ ²¹ ²² ²³ ²⁴ ²⁵ ²⁶ ²⁷ Период полураспада Т1/2 некоторых радиоактивных изотопов (выборочно), калькулятор онлайн, конвертер. Калькулятор – справочный портал. Дата обращения: 7 ноября 2019. Архивировано 7 ноября 2019 года.
↑ Рекорды в науке и технике. Элементы. МОО “Наука и техника”. Дата обращения: 7 ноября 2019. Архивировано 7 ноября 2019 года.
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ M. P. Unterweger, D. D. Hoppes, F. J. Schima, and J. S. Coursey. Radionuclide Half-Life Measurements Data (англ.). NIST (6 сентября 2009). Дата обращения: 26 ноября 2019. Архивировано 3 февраля 2020 года.
↑ Jean-Philippe Uzan. The fundamental constants and their variation: observational status and theoretical motivations. Rev.Mod.Phys. 75(2003)403. arXiv: hep-ph/0205340 Архивная копия от 3 июня 2015 на Wayback Machine.

Ссылки[править | править код]

Наглядное объяснение вероятностной природы экспоненциального распада и периода полураспада как его характеристики

Источник

Загрузить PDF

Периодом полураспада вещества, которое находится в стадии распада, называют время, в течение которого количество этого вещества уменьшится в два раза. Первоначально этот термин использовался для описания распада радиоактивных элементов, таких как уран или плутоний, но, вообще говоря, он может быть использован для любого вещества, которое подвергается распаду в установленной или экспоненциальной скорости. Вы можете рассчитать период полураспада любого вещества, зная скорость распада, которая является разницей между начальным количеством вещества и количеством вещества, оставшимся после определенного периода времени. Читайте далее, чтобы узнать, как быстро и легко подсчитать период полураспада вещества.

1
Разделите количество вещества в одной точке во времени на количество вещества, оставшееся после определенного периода времени.
- Формула для вычисления периода полураспада: t_1/2 = t * ln(2)/ln(N₀/N_t)
- В этой формуле: t – прошедшее время, N₀ – начальное количество вещества и N_t – количество вещества через прошедшее время.
- Например, если вначале количество составляет 1500 граммов, а конечный объем составляет 1000 граммов, начальное количество, деленное на конечный объем, равно 1,5. Предположим, что время, которое прошло, составляет 100 минут, то есть (t) = 100 мин.
2
Вычислите десятичный логарифм числа (log), полученного на предыдущем шаге. Для этого введите полученное число в научный калькулятор, а затем нажмите кнопку log, либо введите log(1,5) и нажмите знак равенства для получения результата.
- Логарифмом числа по заданному основанию называется такой показатель степени, в который необходимо возвести основание (то есть столько раз, сколько необходимо основание умножить на само себя), чтобы получить это число. В десятичных логарифмах используется основание 10. Кнопка log на калькуляторе соответствует десятичному логарифму. Некоторые калькуляторы вычисляют натуральные логарифмы ln.
- Когда log (1,5) = 0,176, то это означает, что десятичный логарифм 1,5 равен 0,176. То есть если число 10 возвести в степень 0,176, то получится 1,5.
3
Умножьте прошедшее время на десятичный логарифм 2. Если вы рассчитаете log(2) на калькуляторе, то получится 0,30103. Следует помнить, что прошедшее время составляет 100 минут.
- Например, если прошедшее время составляет 100 минут, умножьте 100 на 0,30103. Результат равен 30,103.
4
Разделите число, полученное на третьем шаге, на число, вычисленное на втором шаге.
- Например, если 30,103 разделить на 0,176, то получится 171,04. Таким образом, мы получили период полураспада вещества, выраженный в единицах времени, используемых в третьем шаге.
5
Готово. Теперь, когда вы рассчитали период полураспада для этой задачи, необходимо обратить внимание на то, что для расчетов мы использовали десятичный логарифм, но вы могли использовать и натуральный логарифм ln – результат был бы таким же. И, на самом деле, при расчете периода полураспада натуральный логарифм используется чаще.
- То есть, вам было бы необходимо рассчитать натуральные логарифмы: ln(1,5) (результат 0,405) и ln(2) (результат 0,693). Затем, если вы умножите ln(2) на 100 (время), получится 0,693 x 100=69,3, и разделите на 0,405, вы получите результат 171,04 – тот же, что и при использовании десятичного логарифма.
Реклама

1
Узнайте, сколько вещества с известным периодом полураспада осталось через определенное количество времени. Решите следующую задачу: Пациенту было дано 20 мг йода-131. Сколько останется через 32 дня? Период полураспада йода-131 составляет 8 дней. Вот, как решить эту задачу:
- Узнаем, сколько раз вещество сократилось вдвое за 32 дня. Для этого узнаем, сколько раз по 8 (таков период полураспада йода) умещается в 32 (в количестве дней). Для этого необходимо 32/8 = 4, так, количество вещества сокращалось вдвое четыре раза.
- Другими словами, это означает, что через 8 дней останется 20мг/2, то есть 10 мг вещества. Через 16 дней будет 10мг/2, или 5мг вещества. Через 24 дня останется 5мг/2, то есть 2,5 мг вещества. Наконец, через 32 дня у пациента будет 2,5мг/2, или 1,25 мг вещества.
2
Узнайте период полураспада вещества, если известно начальное и оставшееся количество вещества, а также прошедшее время. Решите следующую задачу: Лаборатория получила 200 г технеция-99m и через сутки осталось только 12,5 г изотопов. Каков период полураспада технеция-99m? Вот, как решить эту задачу:
- Будем действовать в обратном порядке. Если осталось 12,5г вещества, тогда прежде, чем его количество сократилось в 2 раза, вещества было 25 г (так как 12,5 x 2); до этого было 50г вещества, а еще до этого было 100г, и, наконец, до этого было 200г.
- Это означает, что прошло 4 периода полураспада прежде, чем от 200 г вещества осталось 12,5 г. Получается, что период полураспада составляет 24 часа/4 раза, или 6 часов.
3
Узнайте, сколько периодов полураспада необходимо для того, чтобы количество вещества сократилось до определенного значения. Решите следующую задачу: Период полураспада урана-232 составляет 70 лет. Сколько периодов полураспада пройдет, чтобы 20 г вещества сократилось до 1,25 г? Вот, как решить эту задачу:
- Начните с 20г и постепенно уменьшайте. 20г/2 = 10г (1 период полураспада), 10г/2 = 5 (2 периода полураспада), 5г/2 = 2,5 (3 периода полураспада) и 2,5/2 = 1,25 (4 периода полураспада). Ответ: необходимо 4 периода полураспада.
Реклама

Предупреждения

Период полураспада – это приблизительное определение времени, необходимого для распада половины оставшегося вещества, а не точный расчет. Например, если остался только один атом вещества, то после полураспада не останется только половина атома, а останется один или ноль атомов. Чем больше количество вещества, тем более точным будет расчет по закону больших чисел

Что вам понадобится

Инженерный калькулятор

Об этой статье

Эту страницу просматривали 55 438 раз.

Была ли эта статья полезной?

Источник

From Wikipedia, the free encyclopedia

Number of half-lives elapsed	Fraction remaining	Percentage remaining
0	1⁄1	100
1	1⁄2	50
2	1⁄4	25
3	1⁄8	12	.5
4	1⁄16	6	.25
5	1⁄32	3	.125
6	1⁄64	1	.5625
7	1⁄128	0	.78125
n	1⁄2ⁿ	100⁄2ⁿ

Half-life (symbol t_½) is the time required for a quantity (of substance) to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable atoms survive. The term is also used more generally to characterize any type of exponential (or, rarely, non-exponential) decay. For example, the medical sciences refer to the biological half-life of drugs and other chemicals in the human body. The converse of half-life (in exponential growth) is doubling time.

The original term, half-life period, dating to Ernest Rutherford’s discovery of the principle in 1907, was shortened to half-life in the early 1950s.^[1] Rutherford applied the principle of a radioactive element’s half-life in studies of age determination of rocks by measuring the decay period of radium to lead-206.

Half-life is constant over the lifetime of an exponentially decaying quantity, and it is a characteristic unit for the exponential decay equation. The accompanying table shows the reduction of a quantity as a function of the number of half-lives elapsed.

Probabilistic nature[edit]

Simulation of many identical atoms undergoing radioactive decay, starting with either 4 atoms per box (left) or 400 (right). The number at the top is how many half-lives have elapsed. Note the consequence of the law of large numbers: with more atoms, the overall decay is more regular and more predictable.

A half-life often describes the decay of discrete entities, such as radioactive atoms. In that case, it does not work to use the definition that states “half-life is the time required for exactly half of the entities to decay”. For example, if there is just one radioactive atom, and its half-life is one second, there will not be “half of an atom” left after one second.

Instead, the half-life is defined in terms of probability: “Half-life is the time required for exactly half of the entities to decay on average“. In other words, the probability of a radioactive atom decaying within its half-life is 50%.^[2]

For example, the image on the right is a simulation of many identical atoms undergoing radioactive decay. Note that after one half-life there are not exactly one-half of the atoms remaining, only approximately, because of the random variation in the process. Nevertheless, when there are many identical atoms decaying (right boxes), the law of large numbers suggests that it is a very good approximation to say that half of the atoms remain after one half-life.

Various simple exercises can demonstrate probabilistic decay, for example involving flipping coins or running a statistical computer program.^[3]^[4]^[5]

Formulas for half-life in exponential decay[edit]

An exponential decay can be described by any of the following four equivalent formulas:^[6]^{: 109–112}

${displaystyle {begin{aligned}N(t)&=N_{0}left({frac {1}{2}}right)^{frac {t}{t_{1/2}}}\N(t)&=N_{0}2^{-{frac {t}{t_{1/2}}}}\N(t)&=N_{0}e^{-{frac {t}{tau }}}\N(t)&=N_{0}e^{-lambda t}end{aligned}}}$

where

N₀ is the initial quantity of the substance that will decay (this quantity may be measured in grams, moles, number of atoms, etc.),
N(t) is the quantity that still remains and has not yet decayed after a time t,
t_½ is the half-life of the decaying quantity,
τ is a positive number called the mean lifetime of the decaying quantity,
λ is a positive number called the decay constant of the decaying quantity.

The three parameters t_½, τ, and λ are directly related in the following way:

${displaystyle t_{1/2}={frac {ln(2)}{lambda }}=tau ln(2)}$

where ln(2) is the natural logarithm of 2 (approximately 0.693).^[6]^: 112

Half-life and reaction orders[edit]

In chemical kinetics, the value of the half-life depends on the reaction order:

Zero order kinetics: The rate of this kind of reaction does not depend on the substrate concentration, [A]:

The integrated rate law of zero order kinetics is:

${displaystyle [{ce {A}}]=[{ce {A}}]_{0}-kt}$

In order to find the half-life, we have to replace the concentration value for the initial concentration divided by 2:

${displaystyle [{ce {A}}]_{0}/2=[{ce {A}}]_{0}-kt_{1/2}}$

and isolate the time:

${displaystyle t_{1/2}={frac {[{ce {A}}]_{0}}{2k}}}$

This t_½ formula indicates that the half-life for a zero order reaction depends on the initial concentration and the rate constant.
First order kinetics: In first order reactions, the concentration of the reactant will decrease exponentially

${displaystyle [{ce {A}}]=[{ce {A}}]_{0}exp(-kt)}$

as time progresses until it reaches zero, and the half-life will be constant, independent of concentration.

The time t_½ for [A] to decrease from [A]₀ to 1/2[A]₀ in a first-order reaction is given by the following equation:

${displaystyle [{ce {A}}]_{0}/2=[{ce {A}}]_{0}exp(-kt_{1/2})}$

It can be solved for

${displaystyle kt_{1/2}=-ln left({frac {[{ce {A}}]_{0}/2}{[{ce {A}}]_{0}}}right)=-ln {frac {1}{2}}=ln 2}$

For a first-order reaction, the half-life of a reactant is independent of its initial concentration. Therefore, if the concentration of A at some arbitrary stage of the reaction is [A], then it will have fallen to 1/2[A] after a further interval of ${displaystyle {tfrac {ln 2}{k}}.}$ Hence, the half-life of a first order reaction is given as the following:

${displaystyle t_{1/2}={frac {ln 2}{k}}}$

The half-life of a first order reaction is independent of its initial concentration and depends solely on the reaction rate constant, k.
Second order kinetics: In second order reactions, the concentration [A] of the reactant decreases following this formula:

${displaystyle {frac {1}{[{ce {A}}]}}=kt+{frac {1}{[{ce {A}}]_{0}}}}$

We replace [A] for 1/2[A]₀ in order to calculate the half-life of the reactant A

${displaystyle {frac {1}{[{ce {A}}]_{0}/2}}=kt_{1/2}+{frac {1}{[{ce {A}}]_{0}}}}$

and isolate the time of the half-life (t_½):

${displaystyle t_{1/2}={frac {1}{[{ce {A}}]_{0}k}}}$

This shows that the half-life of second order reactions depends on the initial concentration and rate constant.

Decay by two or more processes[edit]

Some quantities decay by two exponential-decay processes simultaneously. In this case, the actual half-life T_½ can be related to the half-lives t₁ and t₂ that the quantity would have if each of the decay processes acted in isolation:

${displaystyle {frac {1}{T_{1/2}}}={frac {1}{t_{1}}}+{frac {1}{t_{2}}}}$

For three or more processes, the analogous formula is:

${displaystyle {frac {1}{T_{1/2}}}={frac {1}{t_{1}}}+{frac {1}{t_{2}}}+{frac {1}{t_{3}}}+cdots }$

For a proof of these formulas, see Exponential decay § Decay by two or more processes.

Examples[edit]

There is a half-life describing any exponential-decay process. For example:

As noted above, in radioactive decay the half-life is the length of time after which there is a 50% chance that an atom will have undergone nuclear decay. It varies depending on the atom type and isotope, and is usually determined experimentally. See List of nuclides.
The current flowing through an RC circuit or RL circuit decays with a half-life of ln(2)RC or ln(2)L/R, respectively. For this example the term half time tends to be used rather than “half-life”, but they mean the same thing.
In a chemical reaction, the half-life of a species is the time it takes for the concentration of that substance to fall to half of its initial value. In a first-order reaction the half-life of the reactant is ln(2)/λ, where λ (also denoted as k) is the reaction rate constant.

In non-exponential decay[edit]

The term “half-life” is almost exclusively used for decay processes that are exponential (such as radioactive decay or the other examples above), or approximately exponential (such as biological half-life discussed below). In a decay process that is not even close to exponential, the half-life will change dramatically while the decay is happening. In this situation it is generally uncommon to talk about half-life in the first place, but sometimes people will describe the decay in terms of its “first half-life”, “second half-life”, etc., where the first half-life is defined as the time required for decay from the initial value to 50%, the second half-life is from 50% to 25%, and so on.^[7]

In biology and pharmacology[edit]

A biological half-life or elimination half-life is the time it takes for a substance (drug, radioactive nuclide, or other) to lose one-half of its pharmacologic, physiologic, or radiological activity. In a medical context, the half-life may also describe the time that it takes for the concentration of a substance in blood plasma to reach one-half of its steady-state value (the “plasma half-life”).

The relationship between the biological and plasma half-lives of a substance can be complex, due to factors including accumulation in tissues, active metabolites, and receptor interactions.^[8]

While a radioactive isotope decays almost perfectly according to so-called “first order kinetics” where the rate constant is a fixed number, the elimination of a substance from a living organism usually follows more complex chemical kinetics.

For example, the biological half-life of water in a human being is about 9 to 10 days,^[9] though this can be altered by behavior and other conditions. The biological half-life of caesium in human beings is between one and four months.

The concept of a half-life has also been utilized for pesticides in plants,^[10] and certain authors maintain that pesticide risk and impact assessment models rely on and are sensitive to information describing dissipation from plants.^[11]

In epidemiology, the concept of half-life can refer to the length of time for the number of incident cases in a disease outbreak to drop by half, particularly if the dynamics of the outbreak can be modeled exponentially.^[12]^[13]

References[edit]

^ John Ayto, 20th Century Words (1989), Cambridge University Press.
^ Muller, Richard A. (April 12, 2010). Physics and Technology for Future Presidents. Princeton University Press. pp. 128–129. ISBN 9780691135045.
^ Chivers, Sidney (March 16, 2003). “Re: What happens during half-lifes [sic] when there is only one atom left?”. MADSCI.org.
^ “Radioactive-Decay Model”. Exploratorium.edu. Retrieved 2012-04-25.
^ Wallin, John (September 1996). “Assignment #2: Data, Simulations, and Analytic Science in Decay”. Astro.GLU.edu. Archived from the original on 2011-09-29.{{cite web}}: CS1 maint: unfit URL (link)
^ ^a ^b Rösch, Frank (September 12, 2014). Nuclear- and Radiochemistry: Introduction. Vol. 1. Walter de Gruyter. ISBN 978-3-11-022191-6.
^ Jonathan Crowe; Tony Bradshaw (2014). Chemistry for the Biosciences: The Essential Concepts. p. 568. ISBN 9780199662883.
^ Lin VW; Cardenas DD (2003). Spinal cord medicine. Demos Medical Publishing, LLC. p. 251. ISBN 978-1-888799-61-3.
^ Pang, Xiao-Feng (2014). Water: Molecular Structure and Properties. New Jersey: World Scientific. p. 451. ISBN 9789814440424.
^ Australian Pesticides and Veterinary Medicines Authority (31 March 2015). “Tebufenozide in the product Mimic 700 WP Insecticide, Mimic 240 SC Insecticide”. Australian Government. Retrieved 30 April 2018.
^ Fantke, Peter; Gillespie, Brenda W.; Juraske, Ronnie; Jolliet, Olivier (11 July 2014). “Estimating Half-Lives for Pesticide Dissipation from Plants”. Environmental Science & Technology. 48 (15): 8588–8602. Bibcode:2014EnST…48.8588F. doi:10.1021/es500434p. PMID 24968074.
^ Balkew, Teshome Mogessie (December 2010). The SIR Model When S(t) is a Multi-Exponential Function (Thesis). East Tennessee State University.
^ Ireland, MW, ed. (1928). The Medical Department of the United States Army in the World War, vol. IX: Communicable and Other Diseases. Washington: U.S.: U.S. Government Printing Office. pp. 116–7.

External links[edit]

Look up half-life in Wiktionary, the free dictionary.

Wikimedia Commons has media related to Half times.

https://www.calculator.net/half-life-calculator.html Comprehensive half-life calculator
Welcome to Nucleonica, Nucleonica.net (archived 2017)
wiki: Decay Engine, Nucleonica.net (archived 2016)
System Dynamics – Time Constants, Bucknell.edu
Researchers Nikhef and UvA measure slowest radioactive decay ever: Xe-124 with 18 billion trillion years
https://academo.org/demos/radioactive-decay-simulator/ Interactive radioactive decay simulator demonstrating how half-life is related to the rate of decay

Источник

Download Article

Understanding Half-Life

Learning the Half-Life Equation

Calculating from a Graph

Using a Calculator

Example Problems

Video

Expert Q&A

Tips

The half-life of a substance undergoing decay is the time it takes for the amount of the substance to decrease by half. It was originally used to describe the decay of radioactive elements like uranium or plutonium, but it can be used for any substance which undergoes decay along a set, or exponential, rate. You can calculate the half-life of any substance, given the rate of decay, which is the initial quantity of the substance and the quantity remaining after a measured period of time.^[1]

1
What is half-life? The term “half-life” refers to the amount of time that half of the starting substance takes to decay or change. It’s most often used in radioactive decay to figure out when a substance is no longer harmful to humans.^[2]
- Elements like uranium and plutonium are most often studied with half-life in mind.
2
Does temperature or concentration affect the half-life? The short answer is no. While chemical changes are sometimes affected by their environment or concentration, each radioactive isotope has its own unique half-life that isn’t affected by these changes.^[3]
- Therefore, you can calculate the half-life for a particular element and know for certain how quickly it will break down no matter what.
Advertisement
3
Can half-life be used in carbon dating? Yes! Carbon dating, or figuring out how old something is based on how much carbon it has, is a very practical way to use half-life. Every living thing intakes carbon while it’s alive, so when it dies, it has a certain amount of carbon in its body. The longer it decays, the less carbon is present, which can be used to date the organism based on carbon’s half-life.^[4]
- Technically, there are 2 types of carbon: carbon-14, which decays, and carbon-12, which stays constant.

1

Understand exponential decay. Exponential decay occurs in a general exponential function $f(x)=a^{{x}},$ where ^[5]
2

Rewrite the function in terms of half-life. Of course, our function does not depend on generic variable but time ^[6]
3
4

Solve for the half-life. In principle, the above formula describes all the variables we need. But suppose we encountered an unknown radioactive substance. It is easy to directly measure the mass before and after an elapsed time, but not its half-life. So, let’s express half-life in terms of the other measured (known) variables. Nothing new is being expressed by doing this; rather, it is a matter of convenience. Below, we walk through the process one step at a time.^[8]

1
Read the original count rate at 0 days. Take a look at your graph and find the starting point, or the 0 day mark, on the x-axis. The 0 day mark is right before the material starts decaying, so it’s at its original point.^[9]
- On half-life graphs, the x-axis will usually show the timeline, while the y-axis usually shows the rate of decay.
2
Go down half the original count rate and mark it on the graph. Starting from the top of the curve, note the count rate on the y-axis. Then, divide that number by 2 to get the number at the halfway point. Mark that point on the graph with a horizontal line.^[10]
- For example, if the starting point is 1,640, divide 1,640 / 2 to get 820.
- If you are working with a semi log plot, meaning the count rate is not evenly spaced, you’ll have to take the logarithm of any number from the vertical axis.^[11]
3

Draw a vertical line down from the curve. Starting from the halfway point that you just marked on the graph, draw a second line going downward until it touches the x-axis. Hopefully, the line will touch an easy-to-read number that you can identify.^[12]
4

Read the half-life where the line crosses the time axis. Take a look at the point that your line touched and read where on the timeline it hits. Once you identify the point on your timeline, you’ve found your half-life.^[13]

1
Determine 3 of the 4 relevant values. If you’re solving for half-life, you’ll need to know the initial quantity, the quantity that remains, and the time that has passed. Then, you can use any half-life calculator online to determine the half-life.^[14]
- If you know the half-life but you don’t know the initial quantity, you can input the half-life, the quantity that remains, and the time that has passed. As long as you know 3 of the 4 values, you’ll be able to use a half-life calculator.
2
Calculate the decay constant with a half-life calculator. If you want to calculate how old an organism is, you can input the half-life and the mean lifetime to get the decay constant. This is a great tool to use for carbon dating or figuring out the lifespan of an organism.^[15]
- If you don’t know the half-life but you do know the decay constant and the mean lifetime, you can input those instead. Just like the initial equation, you only need to know 2 of the 3 values to get the third one.
3
Plot your half-life equation on a graphing calculator. If you know your half-life equation and you want to graph it, open up your Y-plots and input the equation into Y-1. Then, hit “graph” to open up your graph and adjust the window until you can see the whole curve. Finally, move your cursor above and below the midpoint of the graph to get your half-life.^[16]
- This is a helpful visual, and it can be useful if you don’t want to do all of the equation work.

1

Problem 1. 300 g of an unknown radioactive substance decays to 112 g after 180 seconds. What is the half-life of this substance?
2

Problem 2. A nuclear reactor produces 20 kg of uranium-232. If the half-life of uranium-232 is about 70 years, how long will it take to decay to 0.1 kg?
3

Problem 3. Os-182 has a half-life of 21.5 hours. How many grams of a 10.0 gram sample would have decayed after exactly 3 half-lives?^[17]
4

Problem 4. A radioactive isotope decayed to 17/32 of its original mass after 60 minutes. Find the half-life of this radioisotope.^[18]

Add New Question

Question

If a sample contains 100 g of a radioactive isotope that has a half-life of 2 days, how much of the isotope remains after 6 days?

Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases.

Scientific Researcher

Expert Answer

Support wikiHow by
unlocking this expert answer.

One quick way to do this would be to figure out how many half-lives we have in the time given.

6 days/2 days = 3 half lives

100/2 = 50 (1 half life)
50/2 = 25 (2 half lives)
25/2 = 12.5 (3 half lives)

So 12.5g of the isotope would remain after 6 days.
Question

If the half-life of a material is 6 hours, how much material remains in 36 hours?

Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases.

Scientific Researcher

Expert Answer
Question

What is the half-life of an isotope that decays to 25% of its original activity in 26.7 hours?

Since the whole is 100%, the first half-life would drop to 50% and then to 25%. Because it takes the isotope 26.7 hours to reach 25%, and there are only 2 halves from 100 to 25%, divide 26.7/2, and you’ll get 13.35 hours as the half life.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

References

About This Article

Article SummaryX

To find the half life of a substance, or the time it takes for a substance to decrease by half, you’ll be using a variation of the exponential decay formula. Plug in ½ for a, use the time for x, and multiply the left side by the initial quantity of the substance. Rearrange the equation so that you’re solving for what the problem asks for, whether that’s half life, mass, or another value. Plug in the values you have and solve, writing the answer in seconds, days, or years. To see the half life equation and look at examples, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,121,337 times.

Reader Success Stories

Georgy Komissarov

Mar 14, 2018

“I am an IB student and am in the process of completing my Math IA. I needed an example of application of number e.…” more

Did this article help you?

Источник

История изучения радиоактивности началась 1 марта 1896 года, когда известный французский ученый Анри Беккерель случайно обнаружил странность в излучении солей урана. Оказалось, что фотопластинки, расположенные в одном ящике с образцом, засвечены. К этому привело странное, обладающее высокой проникающей способностью излучение, которым обладал уран. Это свойство обнаружилось у самых тяжелых элементов, завершающих периодическую таблицу. Ему дали название “радиоактивность”.

Вводим характеристики радиоактивности

Данный процесс – самопроизвольное превращение атома изотопа элемента в иной изотоп с одновременным выделением элементарных частиц (электронов, ядер атомов гелия). Превращение атомов оказалось самопроизвольным, не требующим поглощения энергии извне. Основной величиной, характеризующей процесс выделения энергии в ходе радиоактивного распада, называют активность.

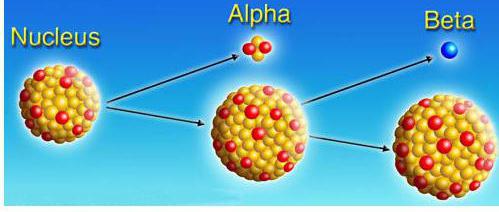
Активностью радиоактивного образца называют вероятное количество распадов данного образца за единицу времени. В СИ (Системе интернациональной) единицей измерения ее назван беккерель (Бк). В 1 беккерель принята активность такого образца, в котором в среднем происходит 1 распад в секунду.

А=λN, где λ- постоянная распада, N – число активных атомов в образце.

Выделяют α, β, γ-распады. Соответствующие уравнения называют правилами смещения:

название	Что происходит	Уравнение реакции
α –распад	превращение атомного ядра Х в ядро Y с выделением ядра атома гелия	_ZА^Х→_Z-2Y^А-4+₂He⁴
β – распад	превращение атомного ядра Х в ядро Y с выделением электрона	_ZА^Х→_Z+1Y^А+_-1e^А
γ – распад	не сопровождается изменением ядра, энергия выделяется в виде электромагнитной волны	_ZХ^А→_ZX^А+γ

Временной интервал в радиоактивности

Момент развала частицы невозможно установить для данного конкретного атома. Для него это скорее «несчастный случай», нежели закономерность. Выделение энергии, характеризующее этот процесс, определяют как активность образца.

Замечено, что она с течением времени меняется. Хотя отдельные элементы демонстрируют удивительное постоянство степени излучения, существуют вещества, активность которых уменьшается в несколько раз за достаточно короткий промежуток времени. Удивительное разнообразие! Возможно ли найти закономерность в этих процессах?

Установлено, что существует время, в течение которого ровно половина атомов данного образца претерпевает распад. Этот интервал времени получил название “период полураспада”. В чем смысл введения этого понятия?

Что такое период полураспада?

Представляется, что за время, равное периоду, ровно половина всех активных атомов данного образца распадается. Но означает ли это, что за время в два периода полураспада все активные атомы полностью распадутся? Совсем нет. Через определенный момент в образце остается половина радиоактивных элементов, через такой же промежуток времени из оставшихся атомов распадается еще половина, и так далее. При этом излучение сохраняется длительное время, значительно превышающее период полураспада. Значит, активные атомы сохраняются в образце независимо от излучения

Период полураспада – это величина, зависящая исключительно от свойств данного вещества. Значение величины определено для многих известных радиоактивных изотопов.

Таблица: «Полупериод распада отдельных изотопов»

Название	Обозначение	Вид распада	Период полураспада
Радий	₈₈Ra²¹⁹	альфа	0,001 секунд
Магний	₁₂Mg²⁷	бета	10 минут
Радон	₈₆Rn²²²	альфа	3,8 суток
Кобальт	₂₇Co⁶⁰	бета, гамма	5,3 года
Радий	₈₈Ra²²⁶	альфа, гамма	1620 лет
Уран	₉₂U²³⁸	альфа, гамма	4,5 млрд лет

Определение периода полураспада выполнено экспериментально. В ходе лабораторных исследований многократно проводится измерение активности. Поскольку лабораторные образцы минимальных размеров (безопасность исследователя превыше всего), эксперимент проводится с различным интервалом времени, многократно повторяясь. В его основу положена закономерность изменения активности веществ.

С целью определения периода полураспада производится измерение активности данного образца в определенные промежутки времени. С учетом того, что данный параметр связан с количеством распавшихся атомов, используя закон радиоактивного распада, определяют период полураспада.

Пример определения для изотопа

Пусть число активных элементов исследуемого изотопа в данный момент времени равно N, интервал времени, в течение которого ведется наблюдение t₂– t₁, где моменты начала и окончания наблюдения достаточно близки. Допустим, что n – число атомов, распавшихся в данный временной интервал, тогда n = KN(t₂– t₁).

В данном выражении K = 0,693/T½ – коэффициент пропорциональности, называющийся константой распада. T½ – период полураспада изотопа.

Примем временной интервал за единицу. При этом K = n/N указывает долю от присутствующих ядер изотопа, распадающихся в единицу времени.

Зная величину константы распада, можно определить и полупериод распада: T½ = 0,693/K.

Отсюда следует, что за единицу времени распадается не определенное количество активных атомов, а определенная их доля.

Закон радиоактивного распада (ЗРР)

Период полураспада положен в основу ЗРР. Закономерность выведена Фредерико Содди и Эрнестом Резерфордом на основе результатов экспериментальных исследований в 1903 году. Удивительно, что многократные измерения, выполненные при помощи приборов, далеких от совершенства, в условиях начала ХХ столетия, привели к точному и обоснованному результату. Он стал основой теории радиоактивности. Выведем математическую запись закона радиоактивного распада.

– Пусть N₀– количество активных атомов в данный момент времени. По истечении интервала времени t нераспавшимися останутся N элементов.

– К моменту времени, равному периоду полураспада, останется ровно половина активных элементов: N=N₀/2.

– По прошествии еще одного периода полураспада в образце остаются: N=N₀/4=N₀/2²активных атомов.

– По прошествии времени, равному еще одному периоду полураспада, образец сохранит только: N=N₀/8=N₀/2³.

– К моменту времени, когда пройдет n периодов полураспада, в образце останется N=N₀/2ⁿ активных частиц. В этом выражении n=t/T½: отношение времени исследования к периоду полураспада.

– ЗРР имеет несколько иное математическое выражение, более удобное в решении задач: N=N₀2^–^t/ ^T½_.

Закономерность позволяет определить, помимо периода полураспада, число атомов активного изотопа, нераспавшихся в данный момент времени. Зная число атомов образца в начале наблюдения, через некоторое время можно определить время жизни данного препарата.

Определить период полураспада формула закона радиоактивного распада помогает лишь при наличии определенных параметров: числа активных изотопов в образце, что узнать достаточно сложно.

Следствия закона

Записать формулу ЗРР можно, используя понятия активности и массы атомов препарата.

Активность пропорциональна числу радиоактивных атомов: A=A₀•2^-t/T. В этой формуле А₀ – активность образца в начальный момент времени, А – активность по истечении t секунд, Т – период полураспада.

Масса вещества может быть использована в закономерности: m=m₀•2^-t/T

В течение любых равных промежутков времени распадается абсолютно одинаковая доля радиоактивных атомов, имеющихся в наличии в данном препарате.

Границы применимости закона

Закон во всех смыслах является статистическим, определяя процессы, протекающие в микромире. Понятно, что период полураспада радиоактивных элементов – величина статистическая. Вероятностный характер событий в атомных ядрах предполагает, что произвольное ядро может развалиться в любой момент. Предсказать событие невозможно, можно лишь определить его вероятность в данный момент времени. Как следствие, период полураспада не имеет смысла:

для отдельного атома;
для образца минимальной массы.

Время жизни атома

Существование атома в его первоначальном состоянии может длиться секунду, а может и миллионы лет. Говорить о времени жизни данной частицы также не приходится. Введя величину, равную среднему значению времени жизни атомов, можно вести разговор о существовании атомов радиоактивного изотопа, последствиях радиоактивного распада. Период полураспада ядра атома зависит от свойств данного атома и не зависит от других величин.

Можно ли решить проблему: как найти период полураспада, зная среднее время жизни?

Определить период полураспада формула связи среднего времени жизни атома и постоянной распада помогает не меньше.

τ= T_1/2/ln2= T_1/2/0,693=1/ λ.

В этой записи τ – среднее время жизни, λ – постоянная распада.

Использование периода полураспада

Применение ЗРР для определения возраста отдельных образцов получило широкое распространение в исследованиях конца ХХ века. Точность определения возраста ископаемых артефактов настолько возросла, что может дать представление о времени жизни за тысячелетия до нашей эры.

Радиоуглеродный анализ ископаемых органических образцов основан на изменении активности углерода-14 (радиоактивного изотопа углерода), присутствующего во всех организмах. Он попадает в живой организм в процессе обмена веществ и содержится в нем в определенной концентрации. После смерти обмен веществ с окружающей средой прекращается. Концентрация радиоактивного углерода падает вследствие естественного распада, активность уменьшается пропорционально.

При наличии такого значения, как период полураспада, формула закона радиоактивного распада помогает определить время с момента прекращения жизнедеятельности организма.

Цепочки радиоактивного превращения

Исследования радиоактивности проводились в лабораторных условиях. Удивительная способность радиоактивных элементов сохранять активность в течение часов, суток и даже лет не могла не вызывать удивления у физиков начала ХХ столетия. Исследования, к примеру, тория, сопровождались неожиданным результатом: в закрытой ампуле активность его была значительной. При малейшем дуновении она падала. Вывод оказался прост: превращение тория сопровождается выделением радона (газ). Все элементы в процессе радиоактивности превращаются в совершенно иное вещество, отличающееся и физическими, и химическими свойствами. Это вещество, в свою очередь, также нестабильно. В настоящее время известно три ряда аналогичных превращений.

Знания о подобных превращениях крайне важны при определении времени недоступности зон, зараженных в процессе атомных и ядерных исследований или катастроф. Период полураспада плутония – в зависимости от его изотопа – лежит в интервале от 86 лет (Pu 238) до 80 млн лет (Pu 244). Концентрация каждого изотопа дает представление о периоде обеззараживания территории.

Самый дорогой металл

Известно, что в наше время есть металлы значительно более дорогие, чем золото, серебро и платина. К ним относится и плутоний. Интересно, что в природе созданный в процессе эволюции плутоний не встречается. Большинство элементов получены в лабораторных условиях. Эксплуатация плутония-239 в ядерных реакторах дала возможность ему стать чрезвычайно популярным в наши дни. Получение достаточного для использования в реакторах количества данного изотопа делает его практически бесценным.

Плутоний-239 получается в естественных условиях как следствие цепочки превращений урана-239 в нептуний-239 (период полураспада – 56 часов). Аналогичная цепочка позволяет накопить плутоний в ядерных реакторах. Скорость появления необходимого количества превосходит естественную в миллиарды раз.

Применение в энергетике

Можно много говорить о недостатках атомной энергетики и о «странностях» человечества, которое практически любое открытие использует для уничтожения себе подобных. Открытие плутония-239, который способен принимать участие в цепной ядерной реакции, позволило использовать его в качестве источника мирной энергии. Уран-235, являющийся аналогом плутония, встречается на Земле крайне редко, выделить его из урановой руды значительно сложнее, чем получить плутоний.

Возраст Земли

Радиоизотопный анализ изотопов радиоактивных элементов дает более точное представление о времени жизни того или иного образца.

Использование цепочки превращений “уран – торий”, содержащихся в земной коре, дает возможность определить возраст нашей планеты. Процентное соотношение этих элементов в среднем по всей земной коре лежит в основе этого метода. По последним данным, возраст Земли составляет 4,6 миллиарда лет.

Источник

Определение и основные соотношения[править | править код]

Парциальный период полураспада[править | править код]

Значения для различных изотопов[править | править код]

Примеры расчётов[править | править код]

Пример 1[править | править код]

Пример 2[править | править код]

Стабильность периода полураспада[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Предупреждения

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Probabilistic nature[edit]

Formulas for half-life in exponential decay[edit]

Half-life and reaction orders[edit]

Decay by two or more processes[edit]

Examples[edit]

In non-exponential decay[edit]

In biology and pharmacology[edit]

See also[edit]

References[edit]

External links[edit]

Video

References

About This Article

Reader Success Stories

Did this article help you?

Вводим характеристики радиоактивности

Временной интервал в радиоактивности

Что такое период полураспада?

Таблица: «Полупериод распада отдельных изотопов»

Пример определения для изотопа

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" alt="период полураспада плутония" src="https://fb.ru/misc/i/gallery/7450/431575.jpg" />

Закон радиоактивного распада (ЗРР)

Следствия закона

Границы применимости закона

Время жизни атома

Использование периода полураспада

Цепочки радиоактивного превращения

Самый дорогой металл

Применение в энергетике

Возраст Земли

Вам также может понравиться

Как найти градусы зная радиан

Как найти пластиковый водопровод под землей

Как в ватсапе найти группы приколов

Добавить комментарий Отменить ответ