Как найди площадь егэ в3

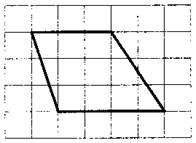
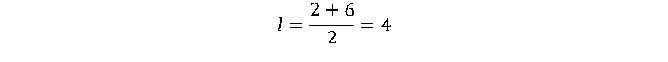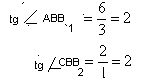За третьим заданием негласно закрепилось название «фигура на бумаге в клетку». В задании представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.

Проверяется знание основ планиметрии: определений, наиболее известных теорем и формул.

Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты

В заданиях встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг.

При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки — надо внимательно читать задание.

По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.

Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.

При подготовке полезно пользоваться прилагающимися к билету справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку.

Определения, а также свойства фигур и их элементов, в справочных материалах не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.

Сложных вычислений в третьем задании нет. Бываю задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще.

Большинство задач можно решить несколькими способами.

Пример №1

Найдите большую диагональ ромба.

Решение: Собственно, все, что нужно знать – определение диагонали и понятие больше-меньше.

Ответ: 4 см.

Удивительно, что в профильной математике встречаются такие задания. И в них тоже допускают ошибки. Видимо, от неожиданности уровня сложности.

Далее для разбора выбраны наиболее сложные задачи, встречавшиеся в третьем задании на экзаменах прошлых лет.

Пример №2

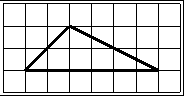
Найдите площадь треугольника.

Решение:

1) Достроим фигуру до прямоугольника. Его площадь равна 6*4=24

2) Найдем площади «лишних» прямоугольных треугольников

(4*4)/2=8 (зеленый)
(2*2)/2=2 (синий)
(6*2)/2=6 (красный)

3) Вычтем из площади прямоугольника лишние площади треугольников: 24-8-2-6=8

Ответ: 8.

Эту же задачу можно решить другим способом.

1) Треугольник является прямоугольным, так как его катеты расположены под углом 45 градусов к вертикальной линии.

2) Катеты найдем из прямоугольных треугольников

Sqrt(4^2+4^2)=4sqrt2 (четыре корня из двух)
Sqrt(2^2+2^2)=2sqrt2 (два корня из двух)

3) Площадь искомого треугольника равна половине произведения катетов: (4sqrt2*2sqrt2)/2=(4*2*2)/2=8

Ответ: 8.

Пример №3

Найдите площадь многоугольника

Решение: Разобьем многоугольник на удобные фигуры и найдем их площади.

Площадь зеленого треугольника 1*3/2=1,5
Площадь синего треугольника 2*1/2=1
Площадь красного треугольника 1*2/2=1
Площадь квадрата 2*2=4
Площадь многоугольника равна их сумме: 1,5+1+1+4=7,5

Ответ: 7,5.

Эту задачу можно решить и вычитанием из площади прямоугольника.

Ответ: 7,5.

Пример №4

Найти площадь многоугольника.

Решение: Можно найти площадь вычитанием, как и в предыдущих заданиях.

Но быстрее можно получить результат с помощью формулы Пика. Для этого нужно сосчитать точки с целыми координатами внутри фигуры (синие) и точки с целыми координатами на контуре фигуры (красные).

Далее к числу точек внутри многоугольника прибавить половину точек на контуре и вычесть единицу.

7+9/2-1=10,5

Ответ: 10,5

Формула Пика не указана в кодификаторе, применять ее при решении заданий с развернутым ответом нельзя. Но в заданиях с кратким ответом она позволяет сэкономить время. Проверьте справедливость формулы на предыдущих примерах.

Пример № 5

Найдите градусную меру угла АВС.

Решение: Точка А имеет нецелые координаты, однако теорема о вписанном и центральном углах позволяет легко решить задачу.

Проведем радиусы в точки А и С.

По рисунку видно, что центральный угол АОС равен 135 градусам. Вписанный угол АВС опирается на те же точки окружности А и С. Согласно теореме, он в два раза меньше центрального.

135/2=67,5

Ответ: 67,5.

Пример №6

Найдите тангенс угла.

Решение: Выделим смежный острый угол.

Выделим прямоугольный треугольник с целочисленными координатами вершин, содержащий этот угол. Найдем тангенс острого угла как отношение противолежащего (зеленого) катета к прилежащему (синему).

tgA=4/1=4

Тангенс смежного тупого угла противоположен по знаку.

Ответ: -4.

В завершении хочется еще раз напомнить: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.

Профессиональный преподаватель также сделал подробный разбор 1 и 2 задания, с которыми можно ознакомиться по ссылкам.

---

Квадратная решетка и координатная плоскость

---

В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках – вычислять параметры фигур – стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.

---

Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.

[/su_note]

Алгоритм решения:

1. Подсчитываем длину основания и высоты.
2. Записываем формулу вычисления площади.
3. Вычисляем площадь.
4. Записываем ответ.

Решение:

1. Подсчитываем длины основания и высоты:

основание = 6,

высота = 2.

2. Записываем формулу площади треугольника: S= ah|2.

3. Вычисляем площадь: S= 6∙2/2=6

Ответ: 6.

---

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

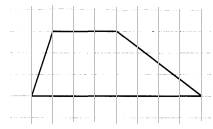
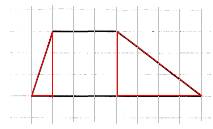
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

1. Подсчитываем длину каждого основания и высоты трапеции.
2. Записываем формулу длины средней линии трапеции.
3. Вычисляем среднюю линию.
4. Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

.

4. Значит, средняя линия равна 3,5.

Ответ: 3,5.

---

Третий вариант задания (из Ященко, №2)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

1. Подсчитываем длину каждого основания и высоты трапеции.
2. Записываем формулу длины средней линии трапеции.
3. Вычисляем среднюю линию.
4. Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 4.

Ответ: 4.

---

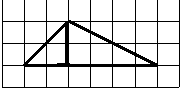
Четвертый вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

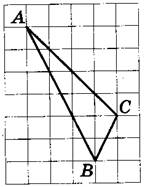
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.

[/su_note]

Алгоритм решения:

1. Проведем перпендикуряры из вершин Аи С.
2. Построим биссектрису угла В.
3. Покажем, что биссектриса параллельна высотам.
4. Измерим длину биссектрисы.
5. Запишем ответ.

Решение:

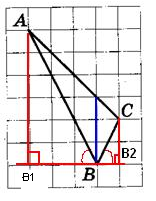
1. Проведем из вершин А и С отрезки АВ₁ иСВ₂, перпендикулярные прямой, содержащей вершину В на рисунке.

2. Построим биссектрису угла B.

3. Рассмотрим треугольники АВВ₁ иВВ₂С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках

Это означает, что углы АВB₁ и СВB₂ равны, так как равны тангенсы этих углов.

Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.

Ответ: 3.

---

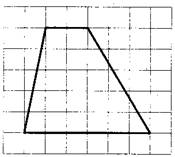
Пятый вариант задания (из Ященко, №7)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

[/su_note]

Алгоритм решения:

1. Рассмотрим рисунок и измерим основания.
2. Проведем высоту.
3. Запишем формулу площади трапеции.
4. Вычислим площадь по формуле.

Решение:

1. На рисунке основания равны 3 и 8.

2. Опустим высоту. Она рана 3.

3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.

4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5

Следовательно, площадь данной трапеции равна 16,5.

Ответ: 16,5.

Даниил Романович | Просмотров: 12.3k

11 августа 2022

В закладки

Обсудить

Жалоба

Разбор основных прототипов задач на нахождение площадей фигур: треугольник, параллелограмм, трапеция, ромб.

planimetria_ploschad_figur.pdf

Автор: Марсель Нуртдинов.

Источник: vk.com/marsel_tutor

Слайд 1

Курсовая работа учителя математики Фадеевой Екатерины Павловны. Информационно-коммуникационное сопровождение обучения математике ПОДГОТОВКА к ЕГЭ -2012. Площади фигур. Решение задач В3. ГБОУ Гимназия № 261 Кировского р-на Санкт-Петербурга.

Слайд 2

ЦЕЛИ : Повторение темы «Площади геометрических фигур» Создание презентации для подготовки уч-ся к экзаменам.

Слайд 3

СОДЕРЖАНИЕ: 1. Разминка . 2. Повторение . 3. Основные типы задач . 5. Тест . 6. Интерактив . 4 . Формула Пика . выход

Слайд 4

Формула Пика 3. Применение формулы для решения задачи 1. 2. Формула Пика. 1. Задача о площади трапеции. 4 . Задачи . содержание

Слайд 5

A B C D S ABCD =S квадрата -(S I +S II +S III +S IV + S кв ) Первый способ: S квадрата = 4·4= 16 ; S I S II S III S IV 1 S I =(4·2):2=4 ; S II= S IV =(1·2):2=1 ; S III =(1·3):2=1,5 ; S кв = 1 . S ABCD =16-(4+1+1,5+1 +1)= 7 ,5 Задача 1 Найти площадь фигуры . Формула Пика содержание

Слайд 6

Формула Пика : Если дан многоугольник на некоторой клетчатой решетке, вершины которого находятся в узлах этой клетчатой решетки , то тогда его площадь можно найти по следующей формуле: S многоугольника = В + Г : 2 – 1 В – кол-во точек пересечения линий решетки внутри фигуры Г – кол-во точек на границе фигуры. задача содержание

Слайд 7

A B D 1 С В = 6 Г = 5 S ABCD = В + Г : 2 – 1 S ABCD = 6 + 5 : 2 – 1 = 7,5 Ответ : 7,5 Задача 1 Найти площадь фигуры . содержание задача

Слайд 8

Заполните пропуски в тексте : 1.Если х 1 ; у 1 и х 2 ; у 2 – данные векторы , то вектор имеет координаты……….. 2. Длина вектора х ; у вычисляется по формуле…….. 3.Если А ( х 1 ; у 1 ) и В ( х 2 ; у 2 )-данные точки, то … 4. Расстояние d между точкой М ( х ; у ) и началом координат выражается формулой … 5.Если даны две точки М 1 ( х 1 ; у 1 ) и М 2 ( х 2 ; у 2 ) ,то расстояние d между ними выражается формулой … х 1 -х 2 ;у 1 -у 2 содержание

Слайд 9

Основные формулы: многоугольник Формула площади Треугольник произвольный а – основание треугольника, h -высота . Прямоугольный треугольник а; в –катеты прямоугольного треугольника Прямоугольник а; в –смежные стороны прямоугольника Трапеция а; в –основания трапеции; h -высота . Круг R – радиус круга. содержание

Слайд 10

B С А D 1 1 ед ² Задача 1 Найти площадь фигуры . S= 1· 8 = 8 ед ² Ответ : 8 . содержание Задача 2

Слайд 11

Задача 2 Найти площадь фигуры . 1 B А С D S =(1 +5) :2 ·4=12 1 ед ² a = 1 Ответ : 12 . b = 5 h = 4 содержание Задача 2 (продолжение)

Слайд 12

Задача 2 Найти площадь фигуры . 1 B А С D S = 1·10 + 4· S Δ 1 ед ² S Δ =1:2 S = 1·10 + 4· (1:2)=12 Ответ : 12 . содержание Задача 3

Слайд 13

A B C H S ABC =S ABH +S BHC S ABC =(1·2):2+(5·2):2=6 Первый способ: Второй способ: S ABC =(BH·AC):2 Задача 3 Найти площадь фигуры . содержание Ответ : 6 . Задача 4

Слайд 14

Задача 4 Найти площадь фигуры . а а= 3 ; h h = 8 ; S = ·a· h = · 3 · 8 = 12 Ответ : 12 . содержание Задача 5

Слайд 15

Задача 5. Найти площадь фигуры . h а h = 5 ; а =3 ; S = ·a· h = · 3 · 5 = 7 ,5 Ответ : 7,5 . содержание Задача 6

Слайд 16

Задача 6 Найти площадь фигуры . а а = 2 ; h = 3 ; h h S = 2 ·S= 2· ·a· h = 2 · 3 = 6 Ответ : 6 . содержание Задача 7

Слайд 17

Задача7 Найти площадь фигуры . содержание A B C D S ADCD = 10·10=100 ед ² S Δ 1 = ·a· h = · 10 ·7 = 35 S Δ 1 S Δ 2 = S Δ 1 S Δ 2 S Δ 3 = ·a· h = · 3 ·3 = 4,5 S = S ADCD – ( S Δ 1 +S Δ 2 + S Δ 3 ) =25,5 Ответ : 25,5 . S Δ 3

Слайд 18

Задача 1 Найти площадь фигуры . содержание Задача 2 В = 10 ; Г = 7 S = В + Г : 2 – 1 S = 10 + 7 : 2 – 1 = 12,5 Ответ : 12,5

Слайд 19

Задача 2 Найти площадь фигуры . Формула Пика S = 12 + 8 : 2 – 1 = 15 Ответ : 15 Первый способ: Второй способ: S = (1 + 4) : 2 ·6 = 15

Слайд 20

www.mathege.ru www.interurok.ru www.reshuege.ru ИНТЕРАКТИВ : содержание

Слайд 21

ЗАДАНИЕ №1 Вариант 1 Вариант 2 Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции. Задание 2

Слайд 22

ЗАДАНИЕ №2 Вариант 1 Вариант 2 Задание 3 Найдите площадь квадрата, вершины которого имеют координаты (4;3), (10;3), (10;9), (4;9). На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

Слайд 23

ЗАДАНИЕ №3 Вариант 1 Вариант 2 Задание 4 Найдите площадь в квадратных сантиметрах. Найдите площадь прямоугольника ABCD , считая стороны квадратных клеток равными 1.

Слайд 24

ЗАДАНИЕ №4 Вариант 1 Вариант 2 Задание 5 Найдите площадь в квадратных сантиметрах. Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.

Слайд 25

ЗАДАНИЕ №5 Вариант 1 Вариант 2 содержание Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет. Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10). ответы

Слайд 26

ОТВЕТЫ к ТЕСТУ 1 2 3 4 5 2 36 7,5 12,5 8 1 2 3 4 5 6 10,5 10 48 25,5 1 вариант 2 вариант содержание

1. Задание В 3 ЕГЭ ПЛАНИМЕТРИЯ: вычисление длин и площадей

Тренажёр
Учитель математики
Байгулова Нина Витальевна
МАОУ СОШ № 58, п. Мулино
Володарский р-н, Нижегородская область

2. Задание B3

Надо знать формулы:
Надо уметь:
площади треугольника;
решать простые
площади
планиметрические
задачи;
производить
вычисления по
известным
формулам.
четырехугольников:
прямоугольника,
квадрата, ромба,
параллелограмма,
трапеции;
площади круга ;
площади сектора.

3. Площадь можно вычислить:

либо по клеточкам,
либо по координатам,
либо по формулам.
Количество баллов за правильное
решение: 1.

4.

S=а·в
S= h(а+в):2
Вычисление
площади
S = π∙ R²
фигуры по
S=0,5ah
формуле

5. Задача 1

Найдите площадь
заштрихованной фигуры, считая
стороны квадратных
клеток равными 1.
4
Ответ: 28
7

6. Задача 2

Найдите площадь ΔABC, считая
стороны квадратных клеток
равными 1.
3
Ответ: 9
6

7. Задача 3

Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
2
3
Ответ: 9
4

8. Задача 4

Найдите площадь треугольника, две
стороны которого равны 4 и 16, а
угол между ними равен 30.
30˚
4
Ответ: 16
16

9. Задача 5

Боковая сторона равнобедренного
треугольника равна 5, а основание
равно 8. Найдите площадь этого
треугольника.
5
Ответ: 12
3
5
4
4
8

10. Задача 6

Найдите площадь ромба, если его
диагонали равны 6 и 10.
6
Ответ: 30
10

11. Задача 7

Найдите площадь S сектора, считая
стороны квадратных клеток
равными 1.
В ответе укажите
S/π .
R√5
1
90˚
Ответ: 1,25
2

12. Задача 8

Найдите площадь сектора круга
радиуса 1, длина дуги которого
равна 2.
2
Ответ: 1
2

13. Задача 9 (Решите сами)

Найдите площадь заштрихованной
фигуры, считая стороны
квадратных клеток равными 1.
Ответ: 14

14. Задача 10 (Решите сами)

Найдите площадь
заштрихованной фигуры, считая
стороны квадратных клеток
равными 1.
Ответ: 15

15. Задача 11 (решите сами)

Периметр треугольника равен 10,
а радиус вписанной окружности
равен 2. Найдите площадь этого
треугольника.
Ответ: 10

16. Задача 12 (решите сами)

Угол при вершине, противолежащей
основанию равнобедренного
треугольника, равен 120. Боковая
сторона треугольника равна 20.
Найдите площадь этого
треугольника. В ответе запишите
S/√3.
Ответ: 100

17. Задача 13(решите сами)

Периметры двух подобных
многоугольников относятся как 3:5.
Площадь меньшего многоугольника
равна 18. Найдите
площадь большего
многоугольника.
Ответ: 50

18.

S₁
S₂
Sфигуры =S₁-S₂
Вычисление
площади
фигуры
через
разность
площадей

19. Полезно знать

Sисх = Sпрямоуг − (S1 + S2 + S3 + S4 + S5)

20. Задача 14

Найти площадь треугольника ABC,
изображенного на рисунке, считая
стороны квадратных клеток равными 1.

21. Задача 14

Решение.
S₁=2,5
Найдем площадь элементов
разбиения:
S1 = ½ · 1 · 5 = 2,5;
S2 = ½ · 3 · 4 = 6;
S2 =6
S3 = ½ · 1 · 4 = 2.
Sпрямоугольника = 5 · 4 = 20.
Найдем площадь исходного треугольника:
Sисх = Sпрямоугольника − (S1 + S2 + S3).
Sисх = 20 − (2,5 + 6 + 2) = 9,5.
5
4
S3 =2
Ответ: 9,5

22. Задача 15

Найдите площадь ΔABC, считая
стороны квадратных клеток
равными 1.
12,5
2
2
Ответ: 7,5
1

23. Задача 16

Найдите площадь ромба ABCD,
считая стороны квадратных клеток
равными 1.
1
1,5
1,5
1,5
Ответ: 8
1,5
1

24. Задача 17

Найдите площадь кольца,
ограниченного концентрическими
окружностями,
радиусы которых
равны 2:√π и 4:√π .
Ответ: 12

25. Задача 18

Найдите площадь S кольца, считая
стороны квадратных клеток равными 1.
В ответе укажите S/π.
2
R
√8
2
Ответ: 4
r=2

26. Задача 19 (Решите сами)

Найдите площадь трапеции ABCD,
считая стороны квадратных клеток
равными 1.
Ответ:9.

27. Задача 20 (Решите сами)

Найдите площадь четырехугольника
ABCD, считая стороны квадратных
клеток равными 1.
Ответ:6

28. Нахождение площади фигуры через сумму площадей

S₁
S₂
Sфигуры
Нахождение
площади
фигуры
через сумму
площадей
=S₁+S₂

29. Задача 21

Найдите площадь прямоугольника
ABCD, считая
стороны квадратных
клеток равными 1.
5
5
Ответ: 10

30. Задача 22

Найдите площадь четырехугольника
ABCD, считая
стороны квадратных
клеток равными 1.
2
4
Ответ:8.

31. Задача 23

Найдите площадь
пятиугольника, считая
стороны квадратных
клеток равными 1.
2
3
Ответ:16.
4

32. Задача 24

Найдите площадь
фигуры, считая
стороны квадратных
клеток равными 1.
1
1
3
4
1
Ответ:15

33. Задача 25

Найдите площадь
фигуры, считая
стороны квадратных
клеток равными 1.
2
1
1
2
Ответ:13.
4
3

34.

у
n
с
к
m
а
Вычисление
х
d площади
в
фигуры по
координатам

35. Задача 26

Найдите площадь треугольника,
вершины которого имеют
координаты
(1; 1), (4; 4), (5;1).
3
Ответ: 6
4

36. Задача 27

Найдите площадь четырехугольника,
вершины которого имеют
координаты (1; 0),
(0; 2), (4; 4), (5; 2) .
2
5
Ответ: 10

37. Задача 28

Найдите площадь закрашенной
фигуры на координатной плоскости.
Ответ: 24

38.

Вычисление
элементов
фигуры
Сторон
Диагоналей
Высот
Углов

39. Задача 29

Найдите сторону квадрата,
площадь которого равна площади
прямоугольника со сторонами
16
4 и 16.
4
Ответ: 8
S=64

40. Задача 30

Найдите диагональ квадрата, если
его площадь равна 8.
4
Ответ: 4
√8
√8

41. Задача 31

Площадь прямоугольного
треугольника равна 21. Один из его
катетов равен 6. Найдите другой
катет.
S=21
Ответ:7.
6

42. Задача 32

Основания равнобедренной
трапеции равны 14 и 26, а ее площадь
равна 160. Найдите периметр
трапеции.
14
S=160
10
8
8
Ответ:60
6
10
6
26

43. Задача 33

Во сколько раз площадь квадрата,
описанного около окружности, больше
площади квадрата, вписанного в эту
окружность?
Ответ: 2

44. Метод координат

А (х₁; у₁)
С (х; у)
α
Метод
координат
В(х₂; у₂)
О
Длина отрезка:
АВ=√(х₁-х₂)²+(у₁-у₂)²
Координаты середины отрезка:
х= (х₁+х₂):2
у= (у₁+у₂):2
Угловой коэффициент k=tg α прямой у=kx+b.

45. Задача 29

1.Найдите длину отрезка, соединяющего точки:
В(-2;2)и A(6, 8);
Ответ:10
2. Найдите расстояние от точки A с координатами
(6, 8) до оси абсцисс;
Ответ:8
Ответ:2
3. Найдите расстояние от точки В до оси ординат.
4. Найдите ординату середины отрезка АВ. Ответ:5
5.Найти ординату точки, симметричной точке А
Ответ:8
относительно оси ОУ;
6. Найти абсциссу точки, симметричной точке А
Ответ:-6
относительно начала координат.

46. Задача 34

Окружность с центром в начале
координат проходит через точку
P(8, 6). Найдите ее радиус.
R
Ответ:10.
6
8

47. Задача 35

Найдите радиус окружности,
описанной около треугольника,
вершины которого имеют
координаты
(8, 0), (0, 6), (8, 6).
R
M
Ответ:5.

48. Задача 36

Найдите :
1)угловой коэффициент прямой,
проходящей через точки с
координатами(2, 0) и (0, 2);
Ответ:-1.
2) угол между
прямой и осью ОХ.
2
Ответ:135.
α
2

49. Задача 37

Точки O(0, 0), A(6, 8), B(6, 2) и C
являются вершинами
параллелограмма. Найдите
ординату точки C.
Ответ:6.

50. Задача 38

Точки O(0, 0), A(10, 8), B(8, 2) и C
являются вершинами
параллелограмма. Найдите абсциссу
точки C.
Ответ:2.
2
8 10

51.

а(х₁; у₁)
А(х₂; у₂)
kа(kх₁; kу₁)
В(х₁; у₁)
Векторы
Координаты вектора АВ(х = х₁ – х₂; у = у₁- у₂)
Длина вектора АВ = √х² + у²= √(х₁-х₂)²+(у₁-у₂)²
Координаты суммы векторов а+b(х₁+х₂ ;у₁+у₂)
Координаты разности векторов а-b(х₁-х₂ ;у₁-у₂)
Координаты вектора умноженного на число:
kа(kх₁; kу₁)

52. Задача 39

Найдите :
Ответ:6
1) ординату вектора а;
2)квадрат длины вектора а;
3) квадрат длины вектора а-b;
4) длину вектора
а+b. Ответ: 10√2
Ответ:40
Ответ:40

53. Задача 40

Вектор с началом в точке A(2, 4)
имеет координаты (6, 2). Найдите
абсциссу точки B.
Ответ:8
8

54. Задача 41

Две стороны прямоугольника ABCD
равны 8 и 6 . Найдите длину суммы
векторов АВ и АД.
6
Ответ:10
8

55. Задача 42

Диагонали ромба ABCD равны 8 и 12.
Найдите длину разности векторов:
1)АВ-АД; Ответ:8
2)АД-АВ; Ответ:8
3)АД+АВ. Ответ:12 .
8
12

56.

Удачи и
успехов!
a a a
m
n
m n
a m a n a m n
ab n
a nb n