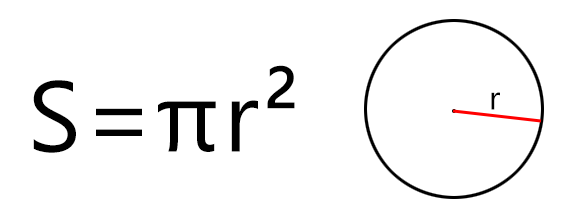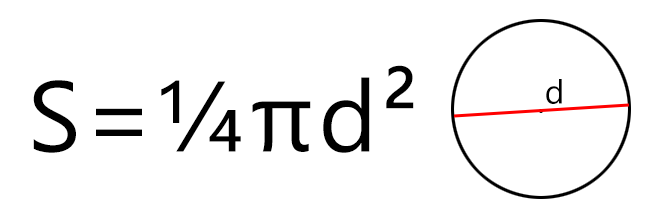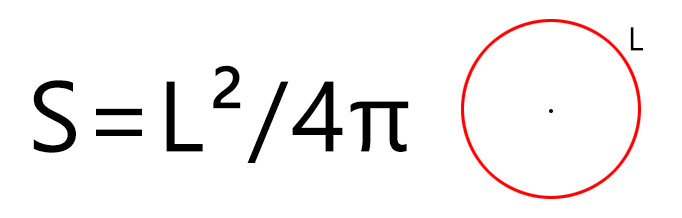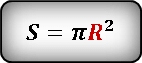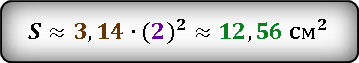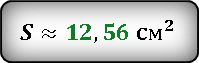Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d – диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L – длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.
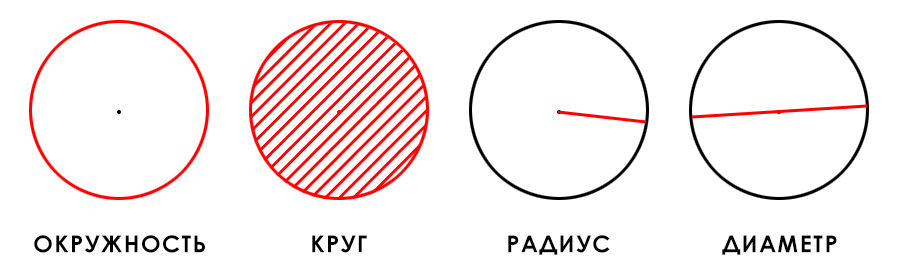
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
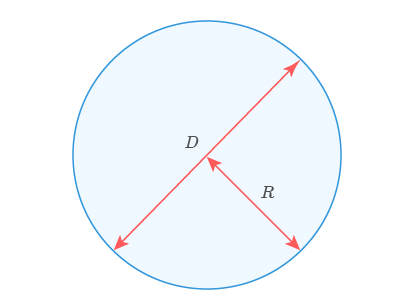
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
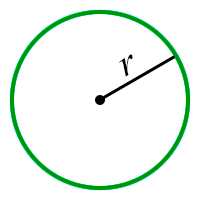
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
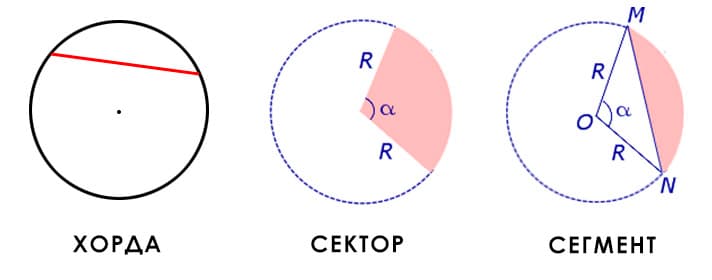
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Окружность – это замкнутая линия, причем расстояние от любой точки, находящейся на этой линии, до центра окружности одинаково. Кругом является внутренняя часть окружности.
Онлайн-калькулятор площади круга
Тот самый отрезок, который соединяет выбранную точку на окружности с ее центром, называется радиусом RR.
Длина радиуса, взятая в двойном размере, называется диаметром окружности DD.
То есть D=2RD=2R.
Как найти площадь круга
Площадь круга можно найти двумя способами:
- используя радиус круга,
- используя диаметр круга.
Остановимся чуть подробнее на каждом способе и рассмотрим несколько примеров.
Формула площади круга через радиус круга
Сначала разберем общий случай.
Пусть нам дана окружность OO произвольного радиуса R.R. Площадь круга через радиус вычисляется при помощи формулы
S=πR2S=pi R^2,
где πpi – число «Пи», выражающее отношение длины окружности к ее диаметру и численно равное около 3,143,14,
RR – радиус нашей окружности.
Теперь, чтобы было более понятно, рассмотрим пару практических примеров.
Найдите площадь круга, радиус которого равен 6 см.
Ответ дайте, округленный до целого числа.
Решение:
Пользуемся нашей формулой для вычисления площади круга и получаем:
S=πR2=3,14⋅6⋅6=3,14⋅36=113.S=pi R^2=3,14cdot 6 cdot 6=3,14 cdot 36=113.
Ответ: 113 см2.
Формула площади круга через диаметр
Рассмотрим сначала обобщенный случай без использования цифр.
Формула вычисления площади круга с помощью диаметра немного отличается от формулы, в которой мы использовали радиус. Но ответ остается, безусловно, таким же.
Итак, наша формула выглядит следующим образом:
S=πD24S=pi frac{D^2}{4}
Давайте разберемся, откуда она вообще взялась.
Для начала выразим радиус через диаметр. Получаем R=D2R=frac{D}{2}, затем подставляем полученное выражение в нашу исходную формулу S=πR2S=pi R^2 и получаем результат: S=πD222S=pi frac{D^2}{2^2}, далее упрощаем и выходим на окончательный ответ S=πD24S=pi frac{D^2}{4}.
Найти площадь круга, если известно, что четвертая часть диаметра равна 2,5 см.
Решение:
Находим диаметр:
D4=2,5.frac{D}{4} =2,5.
Отсюда,
D=2,5⋅4=10.D=2,5 cdot 4=10.
Подставляем значения в формулу:
S=πD24=3,14⋅1024=3,14⋅1004=3,14⋅25=78,5S=pi frac{D^2}{4} =3,14 cdot frac{10^2}{4} =3,14 cdot frac{100}{4} =3,14 cdot 25=78,5
Ответ: 78,5 см2.
Пример решения задачи посложнее.
Имеется два круга. Площадь первого 153,86153,86 см2. Найдите площадь второго круга, радиус которого в 22 раза больше радиуса первого круга.
Решение:
Для решения задачи нам в первую очередь нужно найти радиус первого круга. Из формулы S=πR2S=pi R^2 находим, что R=SπR=sqrt{frac{S}{pi}}.
R=153.863.14=49=7.R=sqrt{frac{153.86}{3.14}}=sqrt{49} = 7.
Радиус второго круга равен 7⋅2=14.7 cdot 2=14.
Наконец, найдем площадь этого круга: S=πR2=3.14⋅142=3,14⋅196=615,44.S=pi R^2=3.14cdot14^2=3,14 cdot 196=615,44.
Ответ: 615,44615,44 см2.
Ищете специалиста, который сможет написать контрольную работу на заказ для вас? Наши эксперты подбирают индивидуальный подход к каждому клиенту!
Тест по теме “Площадь круга”
Площадь Круга через Радиус
Калькулятор рассчитывает Площадь круга по Радиусу. Расчет производится автоматически при вводе величины Радиуса. Подробное решение показывает формулу и порядок вычислений
Радиус Окружности:
Десятичных знаков –
Десят. знаков –
0
Посчитать
Показать решение
Сохранить
П.н.
Сохраненные результаты
Нет сохраненных результатов
Формула площади круга через Радиус

Площадь круга через Радиус
S – площадь круга,
r – радус круга,
π ≈ 3,141592653589
Определения и термины
Круг – множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).
Радиус круга – отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг
Число Пи (π) – математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…
Площадь круга через Диаметр
S – площадь круга,
d – диаметр круга,
π ≈ 3,141592653589
Площадь круга через Радиус
S – площадь круга,
r – радиус круга,
π ≈ 3,141592653589
Площадь круга через Длину Окружности
S – площадь круга,
l – длина окружности,
π ≈ 3,141592653589
Определения и термины
Круг – множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).
Радиус круга – отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг
Диаметр круга – отрезок, соединяющий любые две точки, лежащие на внешней окружности круга, и проходящий через центр круга
Окружность – замкнутая плоская кривая состоящия из всех точек полскости равноудаленных от заданной точки (центра окружности)
Число Пи (π) – математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…
Площадь окружности
Окружность, по своей сути, является границей круга – замкнутой плоской кривой. Из определения следует, что площади окружности не существует,
а существует Площадь круга.
Условие задачи:
Радиус окружности 2 см. Найти площадь круга, ограниченного этой окружностью.
Дано:
Радиус окружности, R = 2 см
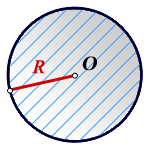
Пояснение к рисунку:
O – -центр окружности
Найти площадь круга: S
Решение
Используем формулу площади круга через радиус.
Подставим значения и вычислим результат.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Калькулятор для расчета площади круга
- Подробности
-
Опубликовано: 04 сентября 2017
-
Обновлено: 13 августа 2021