Как найди площадь нестандартной фигуры

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам 

1. На клетчатой бумаге с размером клетки  изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: 

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

 , где и — диагонали.

Получим: 

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки  

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача.  Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга 

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости 

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S
_ABC = S_ABCD : 2

S
_ABC = 20 : 2 = 10 см²

S
_ABC =
S
_ACD = 10 см²

---

Ваши комментарии

Оставить комментарий:

---

КГУ ЧЕРНОРЕЦКАЯ СОШ № 1

ПАВЛОДАРСКАЯ ОБЛАСТЬ

ПАВЛОДАРСКИЙ РАЙОН

СЕЛО ЧЕРНОРЕЦК

ТЕМІРБУЛАТ НАЗЕРКЕ

8 КЛАСС

НАХОЖДЕНИЕ ПЛОЩАДЕЙ НЕСТАНДАРТНЫХ ФИГУР

НАПРАВЛЕНИЕ: Математическое моделирование экономических и социальных процессов

СЕКЦИЯ: Прикладная математика

Руководитель проекта: учитель математики, педагог-мастер

Середкин В. П.

Научный консультант: к.п.н. ассоциированный профессор (доцент) факультета Computer Science Торайгыров университета

Даниярова Ж.К.

Павлодар, 2022 г.

ОГЛАВЛЕНИЕ

ЭССЕ

АННОТАЦИЯ

РЕЦЕНЗИЯ

ВВЕДЕНИЕ

ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ

СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУРЫ НА КЛЕТЧАТОЙ БУМАГЕ.

ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ ВЫПУКЛОГО МНОГОУГОЛЬНИКА.

РАЗБИЕНИЕ.

ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.

ФОРМУЛА ПИКА.

ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ НЕВЫПУКЛОГО МНОГОУГОЛЬНИКА.

ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.

ФОРМУЛА ПИКА.

МЕТОД МОНТЕ-КАРЛО И ПЛОЩАДИ ФИГУР

СРАВНИТЕЛЬНЫЙ АНАЛИЗ СПОСОБОВ НАХОЖДЕНИЯ ПЛОЩАДИ МНОГОУГОЛЬНИКА НА КЛЕТЧАТОЙ БУМАГЕ.

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

ЭССЕ

В своей работе я рассматриваю вопрос нахождения площадей нестандартных фигур. Все мы знаем определение площади. Площадь указывает размер плоскости, которую занимает фигура. Как мы можем ее найти? Для этого нам нужно знать линейные размеры фигуры и использование геометрические формулы для нахождения площадей. Как определить площадь фигуры неопределенной формы? Для этого можно использовать метод дополнения и разбиения, а можно воспользоваться основной формулой теории вероятности.

Способ разбиение заключается в том, что многоугольник разбивается на прямоугольники и прямоугольные прямоугольники. После нахождения площадей полученных прямоугольников и треугольников, площадь искомого многоугольника находиться путем сложения всех полученных площадей. Способ дополнения основывается на дополнении многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Формула Пика позволяет найти площадь фигуры на клетчатой бумаге. Любая фигура изображенная на с листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника.

Так же площадь многоугольника можно найти, используя основную формулу теории вероятности: вероятность равновероятностного события равна отношению положительных исходов к общему числу исходов

Эта формула легла в основу метода Монте-Карло.

Суть метода Монте-Карло в том, что выбирается некоторая плоскость с известной площадью и на нее переноситься фигура нестандартной формы. Далее на эту плоскость вбрасывается некоторое количество точек и выясняется, сколько точек попало на искомую площадь. Эти данные позволяют воспользоваться формулой вероятности для вычисления искомой площади.

Я думаю что метод Монте-Карло более легкий и удобный ,он находит приближенную площадь. В школьном курсе математики я использую метод Монте-Карло , он позволяет более точно вычислять площадь фигур , только в тех случаях , когда будет задействовано больше количество точек.

АННОТАЦИЯ

В школьном курсе математики мы в основном имеем дело с многоугольниками. С проблемой вычисления площади фигур я столкнулась при решении различных задач, суть которых сводилась к тому, что требовалось найти площадь различных многоугольников, которые мы не рассматривали на уроках математики. При изучении математик до 6 класса мы знакомимся только с формулами для вычисления площади квадрата и прямоугольника. Между тем, на практике часто возникает необходимость найти площадь фигуры неправильной формы. Например, необходимость определить площадь территории по плану или карте. Но для площадей сложных фигур отсутствуют общие формулы, аналогичные формулам для многоугольников.

Гипотеза: площадь сложной фигуры может быть измерена приближенными методами с точностью, достаточной для практических целей.

Цель работы: исследовать различные способы вычисления площадей фигур.

Задачи исследования:

1. Изучить литературу по исследуемой теме;

2. Отобрать интересную и понятную информацию для исследования;

3. Найти способы вычисления площади не стандартных фигур.

Объектом исследования являются методы измерения площади фигур

произвольной формы:

1) способы нахождения площадей;

2) Метод Монте-Карло;

Предметом исследования является площадь фигур произвольной формы.

РЕЦЕНЗИЯ

ВВЕДЕНИЕ

В повседневной жизни мы часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь садового участка и т.д. Необходимость в понятии «площадь» возникла из жизненных потребностей.

В древности люди использовали для измерения длин те измерительные приборы, которые всегда были при себе. Позже возникла потребность в измерении и сравнении разнообразных «фигур», например земельных участков. Было необходимо ввести величину, которая характеризовала бы величину той части плоскости, которую занимает фигура. Эту величину назвали площадью.

Измерение площадей является одним из самых древних разделов геометрии. В частности, название “геометрия” означает “землемерие”, т.е. связано именно с измерением площадей. Основы этой науки были заложены в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, т. е. вычислять их площади. Вавилоняне, так же, как и египтяне измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении стен и насыпей, строительстве плотин и каналов и т.п. Сохранилось немало планов земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также планов различных строений, свидетельствующих, что вавилонский землемер или архитектор должен был хорошо чертить и проводить геометрические расчеты.

Многие ученые решали проблему вычисления площади фигуры. В историю с понятием площади вошли имена Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера Ферма, Георга Пика и др. Ими открыто большое количество различных формул и способов для вычисления площади фигуры.

СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУРЫ НА КЛЕТЧАТОЙ БУМАГЕ.

При изучении вычисления площадей многоугольников на клетчатой бумаге я заметила, что все задачи строятся на понятии узла. Узел напоминает узел в рыболовной сетке – пересечение горизонтальных и вертикальных линий. Все задачи достаточно разнообразны и занимательны, они заставляют думать, размышлять, анализировать, искать аналогии.

Рассмотрим вычисление площади одной и той же фигуры тремя способами и сравним результат вычисления. [1, с.36]

ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ ВЫПУКЛОГО МНОГОУГОЛЬНИКА.

РАЗБИЕНИЕ.

Смысл данного способа состоит в том, что многоугольник разрезается на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. Тогда площадь фигуры можно сосчитать по формуле:

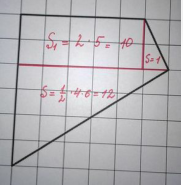
ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.

Смысл данного способа – это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры равна:

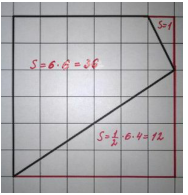
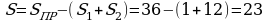
ФОРМУЛА ПИКА.

Любая фигура, изображенная на листе бумаги делит его на внутреннюю область и внешнюю, а еще есть граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые лежат на границе многоугольника. Тогда формула выглядит так

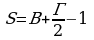
где В – количество внутренних узлов, а Г – количество узлов на границе многоугольника. Эта формула получила название формула Пика в честь австрийского математика Георга Пика которая появилась в его восьмистраничной работе 1899 года, опубликованной в Праге. Используя рисунок В= 17, Г = 14, получаем

Вычисляя площадь выпуклого многоугольника тремя способами, я получила один и тот же результат.

ТРИ СПОСОБА ВЫЧИСЛЕНИЯ ПЛОЩАДИ НЕВЫПУКЛОГО МНОГОУГОЛЬНИКА.

Способ разбиения не подходит для данной фигуры, т.к. невозможно разбить ее на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.

ДОПОЛНЕНИЕ ДО ПРЯМОУГОЛЬНИКА.

Достраивая многоугольник до прямоугольника, и отсекая лишние части, найдем площадь фигуры

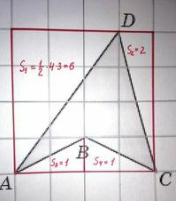
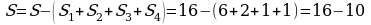
ФОРМУЛА ПИКА.

При подсчете внутренних узлов многоугольника и узлов, лежащих на границе, получим, что В = 5; Г = 4;

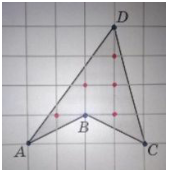
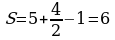
И опять я получила один и тот же результат.

Вычисление площади кольца по формуле Пика.

А если взять не многоугольник, а, например, кольцо и перенести его на клетчатую бумагу? Понятно, что первый и второй способы не удастся использовать. Применим формулу Пика и сравним полученный результат с результатом, полученным используя формулу для вычисления площади круга.

Возьмем кольцо, которое построим с помощью двух окружностей с радиусами R=4 и r = 2.

Вычислим площадь кольца с помощью формулы Пика: В=32, Г=8,

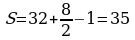
Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.

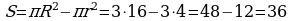
Округлим теперь π до десятых:

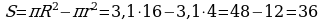
А если округлить число π до сотых, то получим:

Сравнив результаты, можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и чем точнее число π, тем она больше. Следовательно, данную формулу можно применять только для вычисления площадей многоугольников. [2, с.17], [4]

МЕТОД МОНТЕ-КАРЛО И ПЛОЩАДИ ФИГУР

Рассмотрим достаточно интересный метод, который применятся в программировании, алгоритмизации и математике.

Метод основан на применении теории вероятности к алгоритмическим процессам нахождения приближенных значений. Значение отыскиваются путем сравнения результатов равновероятностных событий на два множества, одно из которых полностью включает другое. Полностью включенное множество как раз объявляется как требуемое к отысканию. Более крупное множество, должно быть заведомо с известным значением.

Основная формула теории вероятности: вероятность равновероятного события равна отношению положительных исходов к общему числу исходов

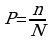
М етод Монте-Карло основан на равновероятном распределении исходов по всему множеству, включающему в себя и неизвестное множество.

Возьмем множество А и множество В которое полностью принадлежит множеству А графически это можно представить в следующем виде рисунок 3.

Исходами в методе Монте-Карло являются выпадения точек в случайных координатах в общее множество часть из которых попадет и во включенное подмножество в формуле вероятности для метода Монте-Карло 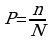, N – это число всех выпавших точек в общее множество, в нашем примере это множество А, а n – это количество этих же точек попавших во множество В.

Если мы проведем подобное для нашей схемы с множествами, расположим на множестве А равновероятным случайные координаты точки то мы увидим что некоторые из них находятся в множестве В их мы и примем за n и можно подсчитать вероятность P это получиться вероятность попадания точек во внутреннее множество.

Как это может помочь при решении задач с площадями? Нам будет необходим следующий постулат – Отношение числа исходов с внутренним множеством которое требуется найти на число исходом с общим множеством приблизительно равно отношению сравниваемых параметром этих множеств в нашем примере отношение числа точек в указанных множествах будет примерно таким же, как и отношение площадей.

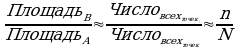
Далее по этой пропорции выражаем площадь В

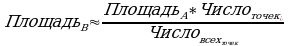
В эту формулу можно будет подставлять числа для расчета.

Р ассмотрим пример: требуется найти площадь листа дерева.

Форма листа клена очень сложная рисунок 5. Вычислить площадь трудно. Но используя метод Монте-Карло данную площадь найти легко.

С формируем основные понятия для этой задачи.

Так как мы ищем площадь кленового листа то это будет искомая площадь В, а общую область нужно выбрать больше с известной площадью например лист А4 рисунок 6. Теперь сформируем общее множество и получим объединенное выражение.

Кладем на сканер лист клена сверху накрываем листом А4 таким образом и лист клена и лист А4 будут в одном разрешении сканируем и получаем изображение рисунок 7.

Используя метод Монте-Карло для нашего изображения. Прокинем на изображение 1000 точек. Из этого числа на лист клена выпало 480 точек. Площадь листа А4 равна 623,7 см². Тогда площадь листа мы сможем вычислить по формуле

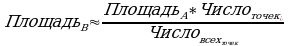
Ниже приводится сравнительная таблица эксперементальных опытов представленной задачи. На основании результатов исследования можно сделать вывод: чем большее количество точек мы будем вбрасывать на плоскость тем точнее будет получаться результат нахождения площади.

СРАВНИТЕЛЬНАЯ ТАБЛИЦА РАСЧЕТОВ
№ опыта	N	n	S(A), кв. см.	S(B), кв. см.
1	1000	480	623,7	299,38
2	1500	700	623,7	291,06
3	2000	950	623,7	296,26
4	2500	1200	623,7	299,38
5	3000	1400	623,7	291,06
6	3500	1650	623,7	294,03
7	4000	1900	623,7	296,26
8	4500	2150	623,7	297,99
9	5000	2400	623,7	299,38
10	5500	2650	623,7	300,51

Р ассмотрим еще один пример применения метода Монте-Карло – задачу нахождения площади острова.

Задача: По аэрофотосъемки некоторой области океана с известной площадью найти приблизительно площадь острова на фото. Известно, что территория на снимке занимает площадь 27 кв.км рисунок 8.

Площадь острова из-за неровных краев и сложной не прямоугольной формы нам неизвестна как же можно, найти, площадь острова не зная функции кривых периметров. В данном случае найти площадь острова нам поможет метод Монте-Карло.

П редположим, что мы кинули на карте 30 случайных точек (рисунок 9) 12 из них попали в область острова также по условию нам известна площадь аэрофотосъемки 27 км² подставим числа в формулу и получаем приближенную площадь острова

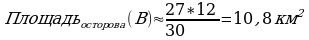
В сравнительной таблице расчетов приводятся результаты экспериментальных опытов. И как в предыдущей задаче с кленовым листом мы приходим к выводу, что при увеличении количества вбрасываемых точек результаты становятся более точными

СРАВНИТЕЛЬНАЯ ТАБЛИЦА РАСЧЕТОВ
№ опыта	N	n	S(A) кв.км.	S(B)кв. км.
1	30	12	27	10,8
2	40	17	27	11,475
3	50	27	27	14,58
4	60	32	27	14,4
5	70	40	27	15,428571
6	80	51	27	17,2125
7	90	64	27	19,2
8	100	72	27	19,44
9	110	81	27	19,881818
10	120	91	27	20,475

СРАВНИТЕЛЬНЫЙ АНАЛИЗ СПОСОБОВ НАХОЖДЕНИЯ ПЛОЩАДИ МНОГОУГОЛЬНИКА НА КЛЕТЧАТОЙ БУМАГЕ.

Разбиение. Этот способ прост в подсчёте площадей фигур, которые разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки. К ним относятся выпуклые многоугольники. К минусам можно отнести то, что в использовании этого способа приходится производить множество действий, а так же невозможность подсчёта площади фигур, которые не разбиваются на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.

Дополнение до прямоугольника. Этот способ так же прост в подсчёте при вычислении площади при небольшом количестве фигур, площадь которых необходимо отнять. Минусы этого способа – сложность подсчёта площади многоугольников необычной формы, большое количество фигур, площадь которых необходимо отнять, а также невозможность подсчёта площади фигур, не относящихся к многоугольникам.

Формула Пика. К плюсам я отнесла то, что легко вычисляется площадь многоугольника с необычной формой, в отличие от предыдущих способов, краткость формулы, а также возможность вычисления приближенного значения площади местности по карте, представив ее в виде многоугольника, перенеся ее на клетку. Минусами этого способа считаю сложность вычисления площади фигуры с большим количеством узлов, а так же, если в фигуре есть «спорные» узлы (узлы, лежащие близко к стороне многоугольника). Вычисляя площадь фигур, не относящихся к многоугольникам, результат получается не точным.

Метод Монте-Карло. Позволяет более точно вычислять площадь фигур, только в тех случаях, когда будет задействовано большое количество точек.

ЗАКЛЮЧЕНИЕ

Изучив различные источники, выяснилось, что существует различные способы вычисления фигур по клеткам, но для меня были интересны и понятны три: разбиение, дополнение до прямоугольника и вычисления по формуле Пика. Также интересным способом нахождения площади произвольной фигуры является метод Монте-Карло.

Моя гипотеза – о том, что если геометрическая фигура изображена на клетчатой бумаге, то ее площадь можно вычислить различными способами и убедиться, что результаты вычислений будут одинаковыми, частично подтвердилась. Рассмотрев все три способа, я пришла к выводу, что не для всякой фигуры можно приметить каждый из них. У каждого из них есть свои плюсы и минусы.

Все три способа можно применить только для выпуклых многоугольников, перенеся их на клетчатую поверхность.

Формула Пика интересна своей простотой. И пусть она при вычислении площадей, не относящихся к многоугольникам, дает приближенное значение, можно легко оценить площадь той или иной территории на карте.

Как оказалось метод Монте-Карло является пригодным для приближенного нахождения площадей фигур сложной формы.

СПИСОК ЛИТЕРАТУРЫ

1. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.

2. История математики с древнейших времен до начала XIX столетия, под редакцией Ю.П. Юшкевича., издательство Наука., М., 1970г

3. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.:

Чистые пруды, 2009.

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

S = a · b

В этой формуле латинской буквой S обозначается площадь, буквами a и b  – стороны прямоугольника.

Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

3 · 5 =
15 (см²)

Ответ: площадь прямоугольника равна 15 см².

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.

4 · 4 =
16 (см²)

Ответ: площадь квадрата равна 16 см².

Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.

Найдите площадь фигуры, изображённой на рисунке.

Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

 А площади прямоугольников мы легко можем найти с помощью
известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 =
20 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6
(см²) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26
(см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 =
12 (см²) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 =
14 (см²) – площадь второго прямоугольника

12 + 14 =
26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Решим следующую задачу.

Найдём площадь ещё одной фигуры, изображённой на рисунке.

Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.

Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 =
14 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3
см.

3 · 3 = 9
(см²) – площадь квадрата

И найдём площадь последнего прямоугольника.

Его ширина равна 3 см. Длина равна 7 см.

3 · 7 =
21 (см²) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.

14 + 9 + 21 =
44 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см²

Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:

И решим ещё одну задачу.

Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.

9 · 5 =
45 (см²) – площадь большего прямоугольника

5 · 3 =
15 (см²) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.

45 – 15 =
30 (см²) – площадь незаштрихованной фигуры

Ответ: площадь незаштрихованной фигуры равна 30 см².