Содержание
- Площадь сечения призмы
- Нахождение площади правильной призмы: формула и задачи
- Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Площадь сечения призмы
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.
Сечение призмы — это изображение фигуры, образованной рассечением призмы плоскостью в поперечном или продольном направлении.

Формула для расчета площади бокового сечения призмы:
a — сторона призмы;
b — высота призмы.
Формула для расчета площади диагонального сечения призмы:
b — высота призмы;
c — диагональ призмы.
Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади бокового или диагонального сечения призмы, если известны длина сторон, диагональ и высота призмы. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения призмы (площадь бокового сечения призмы, площадь диагонального сечения призмы и площадь сечения призмы плоскостью).
Источник
Нахождение площади правильной призмы: формула и задачи
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
» data-lang=»default» data-override=»<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
» data-lang=»default» data-override=»<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Площадь | Формула |
| основание | |
| боковая поверхность | |
| полная |
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a 2 . А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a 2 .
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
» data-lang=»default» data-override=»<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
Привет!
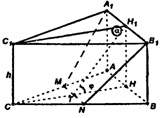
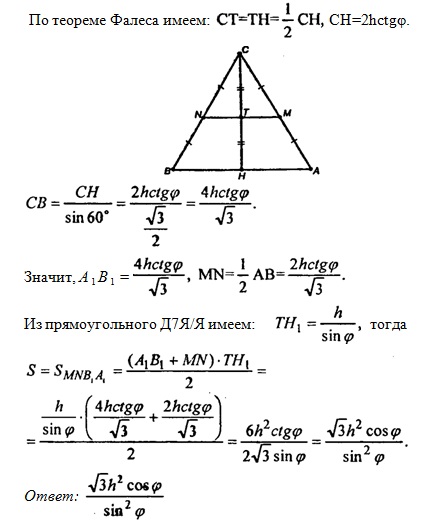
Пусть ΔАВС – правильный,ABC, CC1=h.
Построим линейный угол двугранного угла с ребром MN.
Построим отрезки H1H, TH1
(раз MN || АВ) и
(A1H1=AH, A1H1 || АН, поэтому A1H1HA – параллелограмм с прямым углом A1AH, A1H1HA – прямо угольник) то по теореме о 3-х перпендикулярах имеем: Т1Н1┴ MN.
Тогда линейный угол двугранного данного угла.
4-угольник ABNM- трапеция (MN || A1B1).
Из ΔTHH1 имеем: Н1H:TH=tgα, или
Объем призмы и другие ее характеристики
Перед вами иллюстрированный гид о призме.
В картинках. С пояснениями к формулам. С примерами.
Определение, виды призм, высота, площадь, объем призмы — все, все, все!
Читайте и делитесь впечатлениями в комментариях!
Призма — коротко о главном
Определение призмы:
Призма – это многогранник, две грани которого (основания) – равные многоугольники, лежащие в параллельных плоскостях, а боковые грани – параллелограммы.
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
Виды призм:
Параллелепипед — это призма, основанием которой является параллелограмм.
Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы – равные прямоугольники.
Объем призмы
Главная формула объема призмы:
( displaystyle V=S{{ }_{основания}}cdot text{H}),
где ( {{text{S}}_{основания}}) – площадь основания,
( H) – высота.
Необычная формула объема призмы:
( text{V}={{text{S}}_{bot }}cdot l),
где ( {{text{S}}_{bot }}) – площадь сечения, перпендикулярного боковому ребру,
( l) – длина бокового ребра.
Площадь призмы
Площадь полной поверхности призмы – сумма площадей всех граней.
( displaystyle {{text{S}}_{полн. пов.}}={{text{S}}_{боков.пов.}}+2cdot {{text{S}}_{text{основания}.}})
А теперь чуть подробнее…
Что такое призма
Давай ответим сперва картинками:
Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями.
Остальные грани называются боковыми.
Плоскости оснований параллельный. Боковые грани – параллелограммы.
Рисуем еще раз.
А теперь рёбра.
Смотри: бывают рёбра основания и боковые рёбра.
Важно знать, что:
Все боковые рёбра призмы равны и параллельны.
А еще:
- Если в основании призмы лежит треугольник, то призма называется треугольной, если четырёхугольник, то четырёхугольной и т.д.;
- Бывают и десятиугольные, и двадцатиугольные призмы, но, к счастью, не в твоих задачах;
- А тебе будут встречаться чаще всего треугольные, четырёхугольные и шестиугольные призмы.
Думаю, теперь мы можем дать более строгое определение призмы.
Определение призмы
Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.
Виды призм
Призма, основанием которой является параллелограмм, называется параллелепипедом.
Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания.
Другие призмы называются наклонными.
Высота призмы
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.
Согласен?
Объем призмы
Главная формула объема призмы
( displaystyle V=S{{ }_{основания}}cdot text{H}),где ( {{text{S}}_{основания}}) — площадь основания,
( H) — высота.
Необычная формула объема призмы
( text{V}={{text{S}}_{bot }}cdot l),
где ( {{text{S}}_{bot }}) — площадь сечения, перпендикулярного боковому ребру,
( l) — длина бокового ребра.
Площадь призмы
Площадь полной поверхности призмы – сумма площадей всех граней.
( displaystyle {{text{S}}_{полн. пов.}}={{text{S}}_{боков.пов.}}+2cdot {{text{S}}_{text{основания}.}})
Прямая призма
Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.
Свойства прямой призмы:
- Все боковые грани прямоугольники;
- Все сечения, проходящие через боковые рёбра, – прямоугольники;
- Даже сечения, проходящие только через одно боковое ребро, – прямоугольники;
- У прямой призмы высота совпадает с боковым ребром.
Правильная призма
Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.
То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Тебе, скорее всего, может встретиться:
Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.
Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
Главная формула объема призмы
( displaystyle V=S{{ }_{основания}}cdot text{H})
( {{text{S}}_{основания}}) – площадь основания
( H) – высота
Эта формула верна для любой призмы, но если призма прямая, то ( H) «превращается» в боковое ребро. И тогда
( displaystyle V=S{{ }_{основания}}cdot text{H})
– то же самое, что
( displaystyle V=S{{ }_{основания}}cdot боковое ребро)
Необычная формула объёма призмы
Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы:
( Large text{V}={{text{S}}_{bot }}cdot l)
( {{text{S}}_{bot }}) – площадь сечения, перпендикулярного боковому ребру,
( l) – длина бокового ребра
Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.
Давай теперь для упражнения посчитаем объём самых популярных призм.
Объем правильной треугольной призмы
Пусть дано, что сторона основания равна ( a), а боковое ребро равно ( b).
Найдем объем:
( text{V}={{text{S}}_{Основания}}cdot text{H}={{text{S}}_{text{ABC}}}cdot text{b})
Вспомним, как находить площадь правильного треугольника:
( {{text{S}}_{text{ABC}}}=frac{1}{2}text{a}cdot text{h})
( text{h}=sqrt{{{text{a}}^{2}}-frac{{{text{a}}^{2}}}{4}}=frac{sqrt{3}}{2}text{a})
( {{text{S}}_{text{ABC}}}=frac{1}{2}text{a}cdot frac{sqrt{3}}{2}text{a}=frac{{{text{a}}^{2}}sqrt{3}}{4})
Подставляем в формулу объёма:
( text{V}={{text{S}}_{text{ABC}}}cdot text{b}=frac{{{text{a}}^{2}}text{b}sqrt{3}}{4}).
Объем правильной четырёхугольной призмы
Опять дано: сторона основания равна ( a), боковое ребро равно ( b).
( text{V}={{text{S}}_{text{основания}}}cdot text{H}={{text{S}}_{text{ABC}}}cdot text{b})
Ну, площадь квадрата долго искать не надо:
( displaystyle {{text{S}}_{text{ABCD}}}={{text{a}}^{2}})
Значит, ( displaystyle text{V}={{text{S}}_{text{ABCD}}}cdot text{b}={{text{a}}^{2}}text{b}).
Объем правильной шестиугольной призмы
Площадь поверхности призмы
Площадь боковой поверхности призмы – сумма площадей всех боковых граней.
Есть ли общая формула?
Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – сумма площадей всех граней.
( displaystyle {{text{S}}_{полн. пов.}}={{text{S}}_{боков.пов.}}+2cdot {{text{S}}_{text{основания}.}})
Формулу можно написать для прямой призмы:
( displaystyle {{text{S}}_{боков.}}=text{H}cdot text{P}), где ( displaystyle P) – периметр основания.
( displaystyle {{text{S}}_{text{полной}}}=text{H}cdot text{P}+2{{text{S}}_{основания}}).
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы.
Для примера посчитаем полную поверхность правильной шестиугольной призмы
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
-
3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
Как найти площадь сечения призмы
Призма — это многогранник, основанием которого служат равные многоугольники, боковыми гранями — параллелограммы. Для того чтобы найти площадь сечения призмы, необходимо знать, какое сечение рассматривается в задании. Различают перпендикулярное и диагональное сечение.

Инструкция
Способ расчета площади сечения также зависит от данных, которые уже имеются в задаче. Кроме этого, решение определяется тем, что лежит в основании призмы. Если необходимо найти диагональное сечение призмы, найдите длину диагонали, которая равна корню из суммы (основания сторон в квадрате). Например, если основания сторон прямоугольника равны 3 см и 4 см, соответственно, длина диагонали равна корню из (4х4+3х3)= 5 см. Площадь диагонального сечения найдите по формуле: диагональ основания умножить на высоту.
Если в основании призмы находится треугольник, для вычисления площади сечения призмы используйте формулу: 1/2 часть основания треугольника умножить на высоту.
В случае, если в основании находится круг, площадь сечения призмы найдите умножением числа «пи» на радиус заданной фигуры в квадрате.
Различают следующие виды призм — правильные и прямые. Если необходимо найти сечение правильной призмы, вам нужно знать длину только одной из сторон многоугольника, ведь в основании лежит квадрат, у которого все стороны равны. Найдите диагональ квадрата, которая равна произведению его стороны на корень из двух. После этого перемножив диагональ и высоту, вы получите площадь сечения правильной призмы.
Призма имеет свои свойства. Так, площадь боковой поверхности произвольной призмы вычисляется по формуле, где — периметр перпендикулярного сечения, — длина бокового ребра. При этом перпендикулярное сечение перпендикулярно ко всем боковым ребрам призмы, а его углы — это линейные углы двугранных углов при соответствующих боковых ребрах. Перпендикулярное сечение перпендикулярно и ко всем боковым граням.
Источники:
- диагональное сечение призмы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.