Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🤔 Что это за калькулятор?
Калькулятор площади трапеции — это веб-инструмент, который помогает рассчитать площадь трапеции на основе ее размеров, которые вводит пользователь. Обычно пользователю нужно указать длины двух параллельных сторон трапеции (оснований) и ее высоту.
Калькулятор площади трапеции может быть полезен при решении задач геометрии, в которых необходимо быстро вычислить площадь трапеции. Также он может использоваться при расчетах материалов для строительства и дизайна, где требуется знание площади поверхности трапеции.
🧮 Как работает калькулятор и какие есть примеры использования?
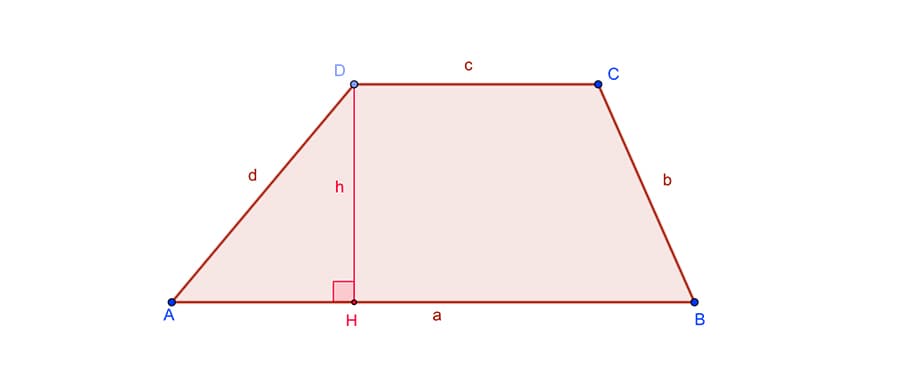
Работа калькулятора площади трапеции основана на формуле, которая используется для расчета площади трапеции. Формула для расчета площади трапеции выглядит следующим образом:
S = (a + b) * h / 2
Где “a” и “b” — это длины оснований трапеции, а “h” – ее высота.
Чтобы использовать калькулятор, пользователь должен ввести длины двух оснований трапеции и ее высоту в соответствующие поля веб-интерфейса калькулятора. После того, как пользователь ввел данные, калькулятор автоматически рассчитывает площадь трапеции и отображает результат на экране.
Пример
Разберем пример использования калькулятора на реальном объекте
Допустим, вы планируете купить ковер для своей гостиной комнаты, и вам нужно знать, какой размер ковра нужен. Ваша гостиная имеет форму трапеции, и вы не знаете, как рассчитать размер ковра, чтобы он идеально соответствовал форме комнаты.
В этом случае вы можете использовать калькулятор площади трапеции для определения площади поверхности пола в гостиной и, следовательно, определения размера ковра, который вам нужен.
Для этого вам необходимо измерить длины двух параллельных сторон комнаты (оснований) и ее высоту. Например, пусть одно основание комнаты равно 6 метров, а другое – 8 метров, а высота составляет 4 метра.
Вводим эти значения в соответствующие поля калькулятора площади трапеции, и получаем результат – площадь гостиной равна 28 квадратных метров.
Теперь вы можете использовать эту информацию, чтобы определить размер ковра, который вам нужен. Например, если вы решили приобрести ковер, покрывающий всю площадь комнаты, то вам понадобится ковер размером, равным 28 квадратных метров.
Также примеры использования калькулятора площади трапеции могут включать следующее:
- Расчет площади трапеции в задачах геометрии на уроках в школе или вузе.
- Расчет площади поверхности трапеции при планировании строительства, например, для расчета необходимого количества материалов.
- Использование калькулятора при разработке дизайна или макетов, когда нужно знать площадь поверхности трапеции для правильного распределения элементов.
- Расчет площади трапеции в повседневной жизни, например, при расчете площади участка земли или для определения площади поверхности торта или пиццы.
Какие виды трапеций существуют
Существует несколько видов трапеций, которые отличаются формой и свойствами сторон и углов. Вот некоторые из них:
- Прямоугольная трапеция — это трапеция, у которой одно основание перпендикулярно к высоте. Углы между боковыми сторонами и основаниями равны по два, как и у прямоугольника.
- Равнобокая трапеция — это трапеция, у которой боковые стороны равны друг другу. Углы между боковыми сторонами и основаниями не равны.
- Равнобедренная трапеция — это трапеция, у которой две боковые стороны и углы между ними равны. Другие две стороны не являются равными и не равны углам между боковыми сторонами и основаниями.
- Криволинейная трапеция — это трапеция, у которой боковые стороны не параллельны друг другу и имеют форму кривых линий.
- Изогнутая трапеция — это трапеция, у которой одно или оба основания имеют изогнутую форму, но боковые стороны все еще параллельны.
Каждый вид трапеции имеет свои уникальные свойства, что делает их полезными в различных математических и геометрических задачах.
Площадь каких видов трапеций может рассчитать наш калькулятор?
Калькулятор площади трапеции может рассчитать площадь всех видов трапеций, включая прямоугольную, равнобокую, равнобедренную, криволинейную и изогнутую трапеции. Для расчета площади трапеции необходимо знать длины ее оснований и высоту. Если речь идет о криволинейной трапеции или изогнутой трапеции, то также необходимо знать длины наклонных боковых сторон.
Калькулятор площади трапеции учитывает все эти параметры и автоматически рассчитывает площадь трапеции, когда вы вводите соответствующие значения в поля веб-интерфейса калькулятора.
❓Вопросы и ответы
При расчете площади трапеции могут возникать различные вопросы. Вот некоторые из наиболее частых вопросов и ответы на них:
Как найти высоту трапеции, если она неизвестна?
Высота трапеции является перпендикулярной линией, проведенной от одного основания до другого. Если вы не знаете высоту, но знаете длины оснований и площадь трапеции, то можно использовать формулу S = (a + b)h/2, где S – площадь, a и b – длины оснований, h – высота. Решая эту формулу относительно h, вы получите высоту трапеции: h = 2S / (a + b).
Как рассчитать площадь криволинейной трапеции?
Чтобы рассчитать площадь криволинейной трапеции, необходимо знать длины ее оснований и наклонных боковых сторон, а также высоту. Затем вы можете использовать формулу для площади трапеции: S = (a + b)h/2, где a и b – длины оснований, h – высота. Для криволинейной трапеции вместо a и b необходимо использовать длины соответствующих наклонных сторон.
Как проверить, что я правильно рассчитал площадь трапеции?
Вы можете проверить правильность своих расчетов, используя формулу для площади трапеции. Также вы можете использовать наш онлайн калькулятор площади трапеции, чтобы проверить свои расчеты. Если вы измерили длины сторон и углы трапеции с помощью инструментов, то также можете проверить свои измерения, сравнив их с теоретическими значениями.
Можно ли рассчитать площадь трапеции, зная только диагонали?
Если вы знаете длины диагоналей трапеции и угол между ними, то можно использовать формулу для расчета площади трапеции: S = (1/2)d1d2sin(theta), где d1 и d2 – диагонали, а theta – угол между ними.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Трапеция – это геометрическая фигура; четырехугольник, имеющий 2 параллельные и 2 непараллельные стороны.
-
Формулы вычисления площади
- По длине оснований и высоте
- Через длины всех сторон (Формула Герона)
- Через диагонали и угол между ними
- Примеры задач
Формулы вычисления площади
По длине оснований и высоте
Площадь трапеции (S) равняется половине суммы ее оснований, умноженной на высоту, проведенную к ним.
![]()
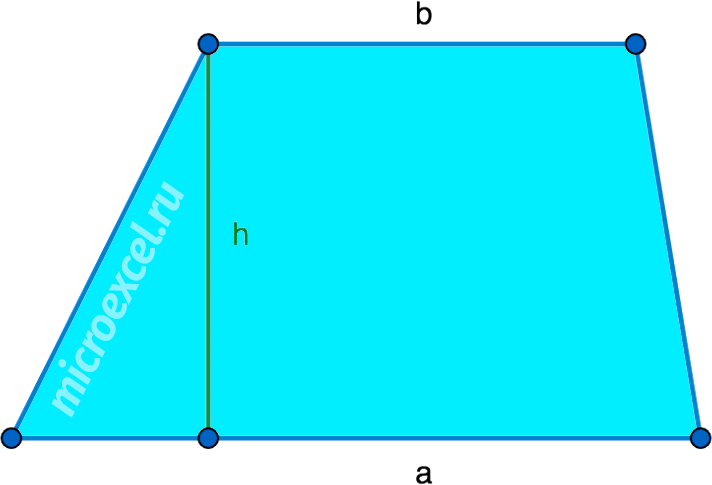
Через длины всех сторон (Формула Герона)
Для вычисления площади трапеции необходимо знать длины всех ее сторон:


p – полупериметр трапеции, считается по формуле:
![]()
Через диагонали и угол между ними
Площадь трапеции равна половине произведения диагоналей и синуса угла между ними. Вычисляется по одной из двух формул ниже:
![]()
![]()

Примеры задач
Задание 1
Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота – 4 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 1/2 * (4 см + 7 см) * 4 см = 22 см2.
Задание 2
Найдите площадь трапеции, если ее основания равны 6 и 12 см, а боковые стороны – 8 и 10 см.
Решение:
Т.к. нам известны длины всех сторон, применим формулу Герона:
S = (6+12) / |6-12| * √(18-6)(18-12)(18-6-8)(18-6-10) = 18 / 6 * √576 = 72 см2.

{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций – обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Площадь трапеции через основания и высоту
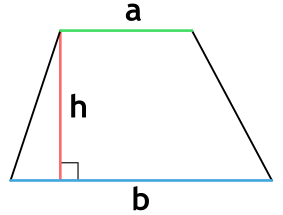
{S = dfrac{1}{2} (a + b) cdot h}
a и b – основания трапеции
h – высота, проведенная к основанию
Площадь трапеции через среднюю линию и высоту
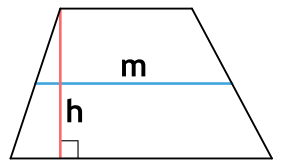
{S = m cdot h}
m – средняя линия трапеции
h – высота трапеции
Площадь трапеции через диагонали и среднюю линию
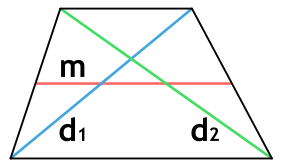
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 – диагонали трапеции
m – средняя линия трапеции
Площадь трапеции через 4 стороны
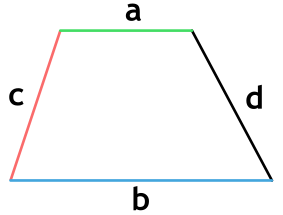
{S = dfrac{a+b}{2} sqrt{c^2 – {Big( dfrac{(a-b)^2 + c^2 – d^2}{2(a-b)} Big)}^2}}
a, b, c и d – стороны трапеции
Площадь трапеции через диагонали и угол между ними
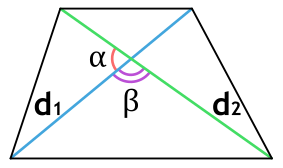
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 – диагонали трапеции
α или β – угол между диагоналями трапеции
Площадь трапеции через основания и углы при основании
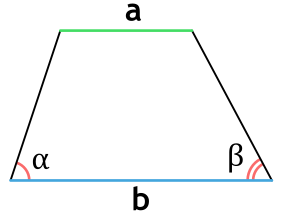
{S = dfrac{b^2 – a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b – основания трапеции
α или β – прилежащие к основанию трапеции углы
Площадь трапеции через площади треугольников
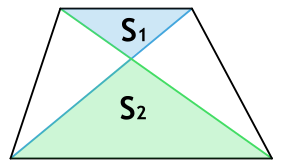
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 – площади образованных пересечением диагоналей трапеции треугольников
Площадь трапеции через диагонали и высоту
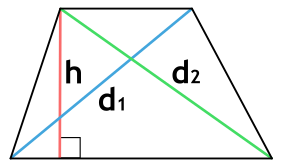
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 – диагонали трапеции
h – высота трапеции
Площадь трапеции через радиус вписанной окружности и основания

{S = (a+b)cdot r}
a и b – основания трапеции
r – радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали

{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 – перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
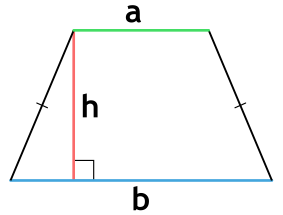
{S = dfrac{a+b}{2} cdot h}
a и b – основания равнобедренной трапеции
h – высота, проведенная к основанию равнобедренной трапеции
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)

{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании

{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a – верхнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
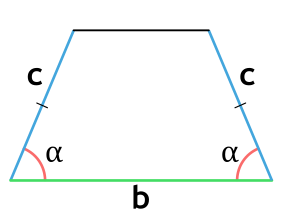
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b – нижнее основание равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – прилежащий к нижнему основанию трапеции угол
Площадь равнобедренной трапеции через основания и угол
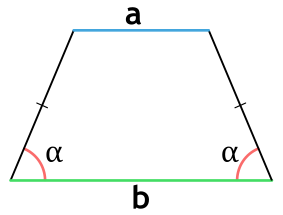
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b – основания равнобедренной трапеции
α – прилежащий к основанию трапеции угол
Площадь равнобедренной трапеции через диагонали и угол между ними
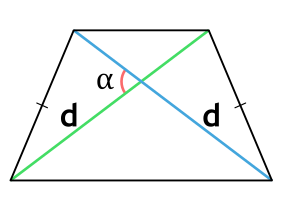
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a – диагональ равнобедренной трапеции
α – угол между диагоналями равнобедренной трапеции
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
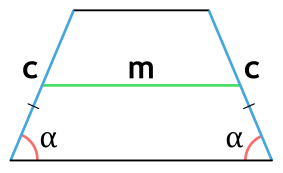
{S = m cdot c cdot sin(alpha)}
m – средняя линия равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании

{S = dfrac{4r^2}{sin(alpha)}}
r – радиус вписанной окружности
α – угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании

{S = dfrac{h^2}{sin(alpha)}}
h – высота равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
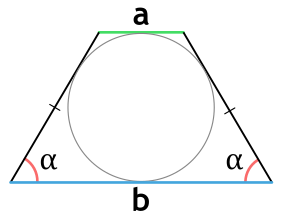
{S = dfrac{a cdot b}{sin(alpha)}}
a и b – основания равнобедренной трапеции
α – угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
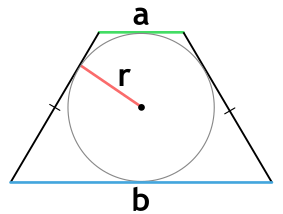
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b – основания равнобедренной трапеции
r – радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания

{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b – основания равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
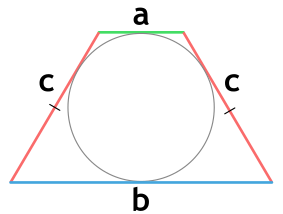
{S = c cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
c – боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
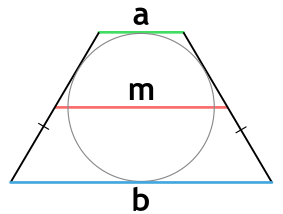
{S = m cdot sqrt{a cdot b}}
a и b – основания равнобедренной трапеции
m – средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h.
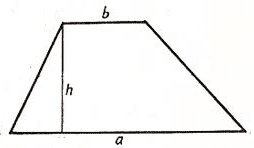
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
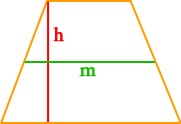
Рассмотрим еще один вариант: в трапеции проведены диагонали d1и d2, которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d1d2 *sinα.
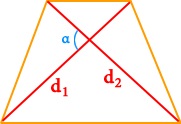
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c2 – ( ( 1/2(b – a)) * ((b – a)2 + c2 – d2) )2.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
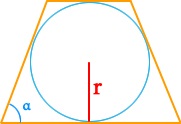
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r2/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 300: S = 8r2.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d1 и d2, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h2.
Формула площади криволинейной трапеции
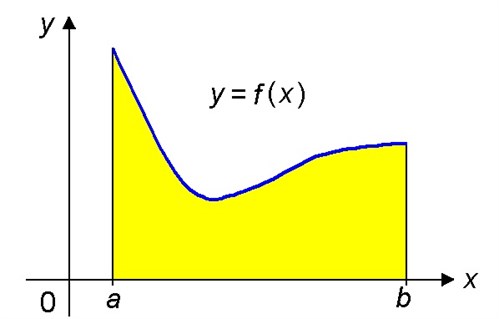
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка [a; b] на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫baf(x)dx = F(x)│ba = F(b) – F(a). В этой формуле F – первообразная нашей функции на выбранном отрезке [a; b]. И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ2 = АР2 + РХ2). И высчитать его площадь: SAPX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см2.
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что SAMPC = SAPX = 54 см2.
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h1 для треугольника ТМЕ и высоту h2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h1 = 1/5(b + х) * h2. Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h1/ h2 = (х – а)/( b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х2 – а2) = (b2 – х2) ↔ 6х2 = b2 + 5а2 ↔ х = √(5а2 + b2)/6.
Таким образом, ОЕ = х = √(5а2 + b2)/6.
Также советуем посмотреть вам наше новое видео по теме нахождения площади фигур, в том числе и трапеции:
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
