Как найди r линейной функции

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

1. Линейная функция пересекает ось (y) в точке (b).
   Примеры:

   

   Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

   Примеры:

   

2. Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

   Примеры:

   

3. Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

   Примеры:

   

Пример (ЕГЭ)

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k<0).

Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.

(k=-frac{AC}{BC}=-frac{1}{3}). Получается (g(x)=-frac{1}{3}x+3).

Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.

Способ 2

Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу (f(x)=kx+b) и решить получившуюся систему уравнений.

Пример (ЕГЭ)

Обозначим жирные точки какими-нибудь буквами и найдем их координаты.

(A(-2;2)) и (B(2;-5)) подставим эти значения вместо (x) и (f(x)) в формулу (f(x)=kx+b):

Получим:

(begin{cases}2=-2k+b\-5=2k+bend{cases})

Теперь найдем (k) и (b), решив эту систему.

Для этого сложим уравнения друг с другом, чтобы исчезло (k):

(2+(-5)=-2k+b+2k+b)
(-3=2b)
(b=-1,5)

Теперь подставим найденное (b) во второе уравнение системы и найдем (k):

(-5=2k-1,5)
(-5+1,5=2k)
(-3,5=2k)
(k=-1,75)

Получается (f(x)=-1,75x-1,5). Остается последний шаг – вычислим при каком иксе функция, то есть (f(x)), равна (16):

(16=-1,75x-1,5)
(17,5=-1,75x)
(x=-10).

Ответ: (-10).

Пример (ЕГЭ)

Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.

Функция (f(x)) возрастает, значит (k>0). (k=+frac{AC}{BC}=frac{4}{4}=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

(begin{cases}4=-2k+b\1=-4k+bend{cases})

Вычтем второе уравнение из первого, чтоб убрать (b):

(4-1=-2k+b-(-4k+b))
(3=2k)
(k=1,5)

Найдем (b):

(4=-2cdot 1,5+b)
(4=-3+b)
(b=7)

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

(x+1=1,5x+7)
(x-1,5x=7-1)
(-0,5x=6)
(x=6:(-0,5))
(x=-12).

Ответ: (-12).

Картинку в хорошем качестве, можно скачать нажав на кнопку “скачать статью”.

Смотрите также:
Как определить a, b и c по графику параболы

Скачать статью

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.

Примеры функций типа «y = kx + b».

• y = 5x + 3
• y = −x + 1
• y = x − 2
• y = 0,5x

Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 5x + 3	k = 5	b = 3
y = −x + 1	k = −1	b = 1
y = 2 3 x − 2	k = 2 3	b = −2
y = 0,5x	k = 0,5	b = 0

Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».

Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.

Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.

Как построить график линейной функции
«y = kx + b»

Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.

Для примера построим график функции «y = −2x + 1».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y = −2x + 1»
0	y(0) = −2 · 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Полученные значения «x» и «y» — это координаты точек графика функции.

Запишем полученные координаты точек «y = −2x + 1» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	1
(·)B	1	−1

Отметим полученные точки на системе координат.

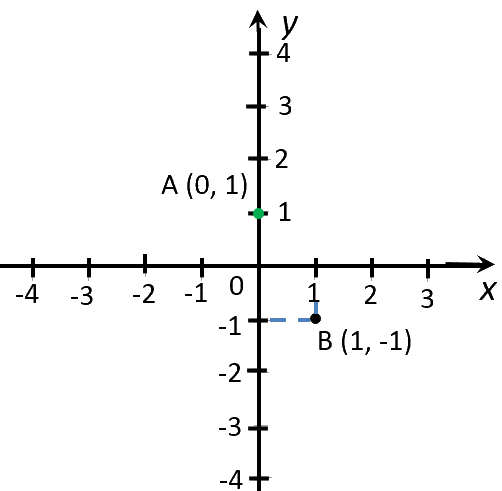
Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».

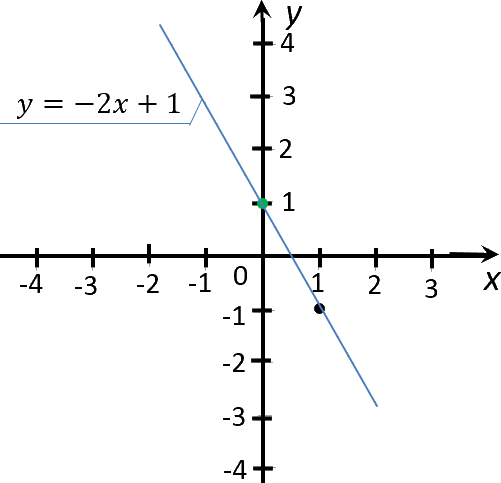
Как решать задачи на
линейную функцию «y = kx + b»

Рассмотрим задачу.

---

Построить график функции «y = 2x + 3». Найти по графику:

1. значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
2. значение «x», если значение «y» равно
   1; 4; 0; −1.

---

Вначале построим график функции «y = 2x + 3».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = 2 · 0 + 3 = 3
(·)B	1	y(1) = 2 ·1 + 3 = 5

Отметим полученные точки на прямоугольной системе координат.

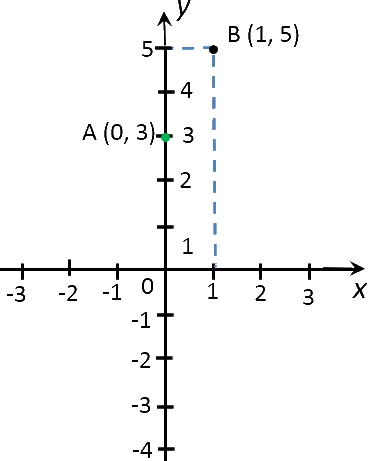
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».

---

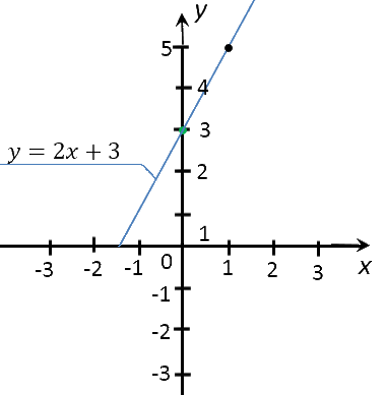
Теперь работаем с построенным графиком функции «y = 2x + 3».

Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.

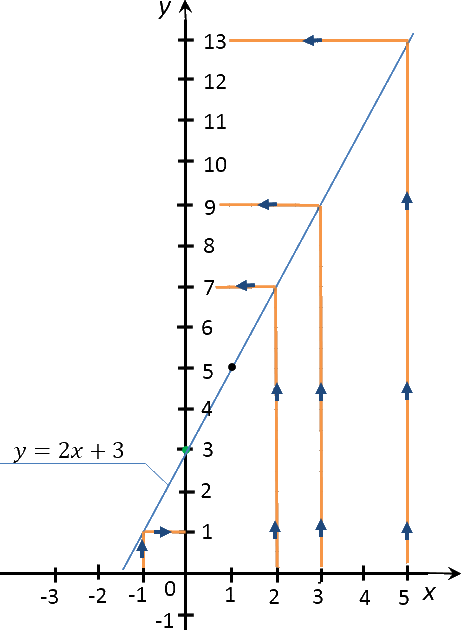
Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
−1	1
2	7
3	9
5	13

---

Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».

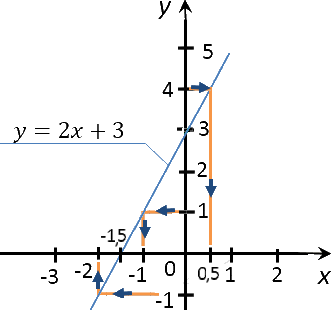
Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−1	−2
0	−1,5
1	−1
4	0,5

---

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).

---

Подставим в функцию
«y = 2x −
»

координаты точки (0;
− ).

− = 2 · 0
−

   − =
−

(верно)

Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).

---

Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».

−2 = 2 · 1 −

−2 = 2 −

−2 = 1 −

        −2 = 1 (неверно)

Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).

---

Как найти точки пересечения графика с осями

Рассмотрим задачу.

Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.

Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.

Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».

Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 + 3 = 3
(·)B	1	y(1) = −1,5 · 1 + 3 = 1,5

Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».

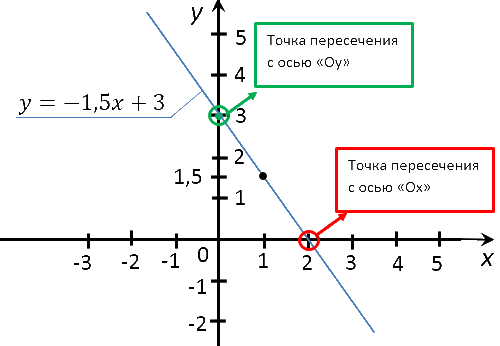
Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.

y(0) = −1,5 · 0 + 3 = 3

(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».

Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.

0 = −1,5x + 3        
1,5x = 3        | :(1,5)
x = 3 : 1,5           
x = 2                   

(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».

---

Ваши комментарии

Оставить комментарий:

---

Линейная функция

Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: деньги – зарплата, вес – круассаны, расстояние – время.

Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).

То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).

Что значит «допустимому»?

Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.

Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.

Ну и вернемся, наконец, к теме данной статьи.

Линейной называется функция вида ( y=kx+b), где ( k) и ( b) ­– любые числа (они называются коэффициентами).

Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.

Как думаешь, почему она называется линейной?

Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.

Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения ( Dleft( y right)) и область значений ( Eleft( y right)).

Область значений линейной функции

Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент ( x), тем больше значение функции ( y).

Значит, ( y) так же как и ( x) может принимать все возможные значения, то есть ( Eleft( y right)=mathbb{R}), верно?

Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?

Вспомним формулу: ( y=kx+b). Какие нужно выбрать коэффициенты ( k) и ( b), чтобы значение функции y не зависело от аргумента ( x)?

А вот какие: ( b) – любое, но ( k=0). И правда, каким бы ни был аргумент ( x), при умножении на ( k=0) получится ( 0)!

Тогда функция станет равна ( y=0cdot x+b=b), то есть она принимает одно и то же значение при всех ( x):

( y = kx + b:{rm{ }}left[ begin{array}{l}Eleft( y right) = mathbb{R}{rm{ при }}k ne 0\Eleft( y right) = left{ b right}{rm{ при }}k = 0.end{array} right.)

Теперь рассмотрим несколько задач на линейную функцию.

График линейной функции

Как я уже упоминал ранее, график такой функции – прямая линия.

Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).

Предположим, у нас есть функция линейная функция ( y=2x+1). Чтобы построить ее график, нужно вычислить координаты любых двух точек.

То есть нужно взять любые два значения аргумента ( x) и вычислить соответствующие два значения функции.

Затем для каждой пары ( left( x;y right)) найдем точку в системе координат, и проведем прямую через эти две точки.

Проще всего найти функцию, если аргумент ( x=0:yleft( 0 right)=2cdot 0+1=1).

Итак, первая точка имеет координаты ( left( 0;1 right)).

Теперь возьмем любое другое число в качестве ( x), например, ( x=1:yleft( 1 right)=2cdot 1+1=3).

Вторая точка имеет координаты ( left( 1;3 right)).

Ставим эти две точки на координатной плоскости:

Теперь прикладываем линейку, и проводим прямую через эти две точки:

Вот и все, график построен!

Давай теперь на этом же рисунке построим еще два графика: ( y={x} -1) и ( y=-x+2).

Построй их самостоятельно так же: посчитай значение y для любых двух значений ( x), отметь эти точки на рисунке и проведи через них прямую.

Должно получиться так:

Коэффициенты линейной функции

Для начала выясним, что делает коэффициент ( displaystyle b). Рассмотрим функцию ( displaystyle y=x+b), то есть ( displaystyle k=1).

Меняя ( displaystyle b) будем следить, что происходит с графиком.

Итак, начертим графики для разных значений ( displaystyle b:b=-2,text{ -}1,text{ }0,text{ }1,text{ }2):

Что ты можешь сказать о них? Чем отличаются графики?

Это сразу видно: чем больше ( displaystyle b), тем выше располагается прямая.

Более того, заметь такую вещь: график пересекает ось ( displaystyle mathbf{y}) в точке с координатой, равной ( displaystyle mathbf{b})!

И правда. Как найти точку пересечения графика с осью ( displaystyle y)? Чему равен ( displaystyle x) в такой точке?

В любой точке оси ординат (это название оси ( displaystyle y), если ты забыл) ( displaystyle x=0).

Значит достаточно подставить ( displaystyle x=0) в функцию, и получим ординату пересечения графика с осью ( displaystyle y):

Построим графики для ( displaystyle k=-3,text{ -}1,text{ }0,text{ }1,text{ }2:)

Так, теперь ясно: ( displaystyle k) влияет на наклон графика.

Чем больше ( displaystyle k) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – ( displaystyle Ox)) расположена прямая.

Если ( displaystyle k>0), график наклонен «вправо», при ( displaystyle k<0) – «влево». А когда ( displaystyle k=0), прямая располагается вдоль оси абсциссс.

Давай разбираться. Начертим новый график ( displaystyle y=kx+b):

Выберем на графике две точки ( displaystyle A) и ( displaystyle B). Для простоты выберем точку ( displaystyle A) на пересечении графика с осью ординат. Точка ( displaystyle B) – в произвольном месте прямой, пусть ее координаты равны ( displaystyle left( x;y right)).

Рассмотрим прямоугольный треугольник ( displaystyle ABC), построенный на отрезке ( displaystyle AB) как на гипотенузе.

Из рисунка видно, что ( displaystyle AC=x), ( displaystyle BC=y-b).

Подставим ( displaystyle y=kx+b) в ( displaystyle BC:BC=y-b=kx+b-b=kx).

Получается, что ( BC = k cdot AC{rm{ }} Rightarrow {rm{ }}k = frac{{BC}}{{AC}} = {mathop{rm tg}nolimits} alpha ).

Итак, коэффициент ( displaystyle k) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.

Именно поэтому его (коэффициент ( displaystyle k)) обычно называют угловым коэффициентом.

В случае, когда ( k < 0,{mathop{rm tg}nolimits} alpha < 0,) что соответствует тупому углу:

Если же ( displaystyle k=0), тогда и ( {mathop{rm tg}nolimits} alpha = 0,) следовательно ( displaystyle alpha =0), то есть прямая параллельна оси абсцисс.

Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.

На прошлых уроках мы рассмотрели линейную функцию и научились строить ее график на координатной плоскости. На этом уроке мы углубимся в теорию и разберем, почему график выглядит именно так.

Вспомним, что линейная функция имеет вид $y = kx+b$, где $x$ – переменная, а $k$ и $b$ – некоторые числа, называемые коэффициентами.

Например,

• $y = textcolor{blue}{5}x + color{green}{10}$ – линейная функция
• $color{blue} k = 5$
• $color{green} b = 10$.

График линейной функции – прямая линия, а ее положение на плоскости зависит от того, какие у функции $k$ и $b$.

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат. 

Другими словами, коэффициент $b$ показывает, насколько график выше или ниже оси $Oy$.

• Если $b > 0$, график сдвинут вверх,
• если $b < 0$, то график сдвинут вниз.

На нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

Частные случаи. b = 0

Если коэффициент $b = 0$, функция приобретает вид $y = kx + 0$, что можно сократить до $y = kx$.

Подставим в формулу $x = 0$, получим: $$y = k times 0$$

Значит, график будет проходить через начало координат $O(0;0)$.

Для построения графика функции вида $y = kx$ достаточно найти одну точку, вторая – начало координат.

k = 0

Если коэффициент $k = 0$, угол наклона также будет равен $0$.

Функция при этом принимает вид $y = 0 times x + b$, то есть $y = b$.

Куда делась переменная $x$? Она нам больше не нужна, так как какой бы $x$ мы не подставили, значение $y$ не изменится.

Таблица

Определение

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

1. Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
2. Областью значений также является множество всех действительных чисел.
3. Функция не имеет ни наибольших, ни наименьших значений.
4. При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
5. При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
6. При k=0 прямая параллельна оси х.
7. Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

у=2х – 1=2×0 – 1= –1;

у=2х – 1=2×3 – 1= 5.

Вписываем в таблицу значения у:

Теперь строим систему координат, отмечаем в ней точки с координатами      А(0; –1) и В(3;5), проводим через эти две точки прямую.

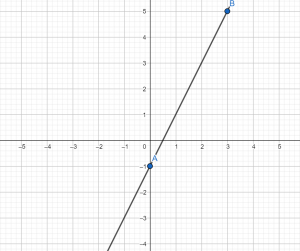
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

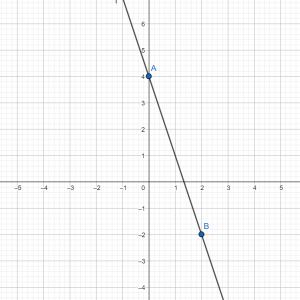
Пример №3

Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

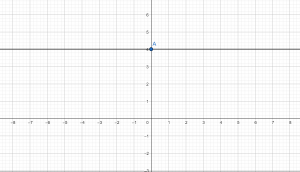
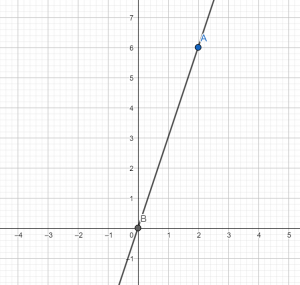
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.

Задание OM1106o

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ГРАФИКИ:

КОЭФФИЦИЕНТЫ:

1) k>0, b<0                   2) k>0, b>0                    3) k<0, b<0 

---

ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>90⁰) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.

У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<90⁰). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

Ответ: 213

pазбирался: Даниил Романович | обсудить разбор

Задание OM1103o

Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x

Б) y = -3x

В) y = (1/3)x

Графики:

---

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

y = kx + b

График данной функции зависит от k и b.

• если k < 0,  то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
• если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
• коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если  b > 0, то выше ноля в точке y = b
• если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1

Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 6k