Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Найдите градусную величину дуги
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:
По клетчатой сетке видно, что угол АОС равен 45 0 . Это и есть градусная величина дуги АС.
27891.Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.
*Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС.
По клетчатой сетке видно, что угол ВОС равен 90 0 + 45 0 = 135 0 .
Как определить величину дуги окружности
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Площадь круга и его частей. Длина окружности и ее дуг
| Основные определения и свойства. Число π |
| Формулы для площади круга и его частей |
| Формулы для длины окружности и ее дуг |
| Площадь круга |
| Длина окружности |
| Длина дуги |
| Площадь сектора |
| Площадь сегмента |
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |
,
где R – радиус круга, D – диаметр круга
Площадь сектора
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Площадь сегмента
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
,
где R – радиус круга, D – диаметр круга
Площадь сектора
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Площадь сегмента
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула |
| Длина окружности |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
[spoiler title=”источники:”]
http://matematikaege.ru/vpisaniy-ugol/27890-najdite-gradusnuyu-velichinu-dugi.html
http://b4.cooksy.ru/articles/kak-opredelit-velichinu-dugi-okruzhnosti
[/spoiler]
Дуга окружности – это фрагмент окружности. Если на окружности отметить две точки A И B, то она разобьётся на 2 части, называемые дугами окружности.

Для того, чтобы найти длину дуги окружности, необходимо использовать значение центрального угла, измеряемого в радианах или градусах.
Существует 2 формулы длины дуги окружности:
1) Если дан центральный угол в радианах: l = R*α, где R – радиус, α – величина угла AOB в радианах.
2) Если дан центральный угол в градусах: l = R*π*C/180, где R – радиус, C – величина угла AOB в градусах.
Пример
Дано:
1) радиус окружности R = 6 дм.
2) центральный угол AOB = 45°.
Найти:
Длину дуги AB.
Решение:
l = 6*3,14*1/4 дм. = 4,71 дм.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое длина дуги?
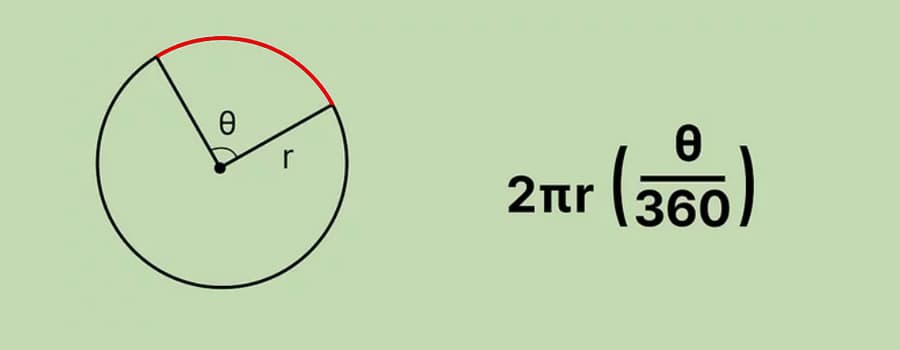
Дуга — это часть окружности, ограниченная двумя точками на окружности.
Для вычисления длины дуги необходимо знать радиус окружности и центральный угол, охватывающий эту дугу.
Наш онлайн калькулятор длины дуги может вычислить длину дуги через угол в градусах и радианах.
Для вычисления длины дуги через центральный угол в градусах формула выглядит следующим образом:
L = r * θ * π / 180
где L – длина дуги, r – радиус окружности, θ – центральный угол в градусах, π – число Пи (3.14159…).
Для вычисления длины дуги через центральный угол в радианах формула выглядит следующим образом:
L = r * θ
где L – длина дуги, r – радиус окружности, θ – центральный угол в радианах.
Таким образом, чтобы использовать наш калькулятор для вычисления длины дуги через центральный угол в градусах, необходимо ввести радиус и угол в градусах, а для вычисления длины дуги через центральный угол в радианах – радиус и угол в радианах.
🔣 Формула Гюйгенса
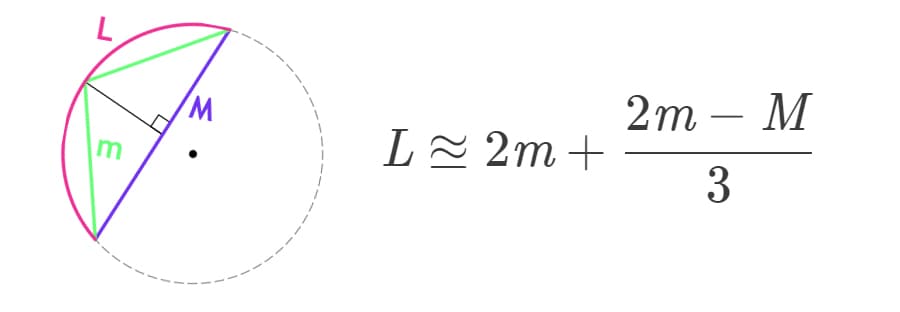
Длину дуги можно найти, используя более редкую формула, в которой известны две хорды, как показано на рисунке выше. Это формула называется формулой Гюйгенса.
В формуле Гюйгенса используется знак “равно или почти равно” (≊), потому что вычисления с помощью этой формулы могут содержать погрешности. Эти погрешности обычно малы, но они существуют, и их нужно учитывать. Относительная погрешность формулы Гюйгенса составляет около 0,5% при угле дуги в 60°. Однако, при уменьшении угла дуги, погрешность также уменьшается. Например, при дуге в 45° относительная погрешность составит около 0,02%.
🌈 Пример использования калькулятора в повседневной жизни
Калькулятор для вычисления длины дуги может быть использован и в повседневной жизни в различных ситуациях:
Пример 1. При выборе размера ободной обрезиненной ленты для замены на велосипеде. Чтобы выбрать правильный размер ленты, необходимо знать длину окружности колеса. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить длину окружности колеса по его радиусу.
Пример 2. При планировании работы садовой или дачной зоны. Например, при расчете длины ленточного газона или длины обочин для дорожек. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить необходимую длину материала.
Пример 3. При выборе длины троса для подвешивания карниза или штор в доме. Чтобы подобрать правильную длину троса, необходимо знать длину окна и расстояние от карниза до пола. Калькулятор для вычисления длины дуги поможет быстро и точно вычислить длину троса, необходимую для подвешивания карниза.
Помимо этого, калькулятор для вычисления длины дуги может быть использован для быстрого и удобного решения задач, связанных с геометрией, физикой и техническими науками. Например:
- Геометрия: в геометрии часто требуется вычислять длину дуги окружности для построения различных фигур и геометрических конструкций.
- Физика: в физике, например, длина дуги может быть использована для вычисления длины траектории движения тела по окружности.
- Технические науки: в инженерии и других технических науках, вычисление длины дуги может быть использовано для определения размеров и формы кривых поверхностей и для расчета траекторий движения механизмов и устройств.
Таким образом, калькулятор для вычисления длины дуги может быть полезным инструментом как в повседневной жизни, так и при решении задач, связанных с техническими науками.
🌀 Основные виды дуг
- Дуги окружности — это дуги, которые образуются на окружности. Они имеют равные начальный и конечный углы и могут быть выражены через радиус окружности и центральный угол, который они охватывают.
- Произвольные дуги — это дуги, которые не являются частью окружности и могут быть описаны любой кривой. Они могут быть параметризованы, то есть выражены через параметр, который изменяется от начального до конечного значения. (Примеры произвольных дуг включают дуги эллипсов, парабол, гипербол и других кривых, которые можно параметризовать).
- Круговые дуги — это дуги, которые образуются на круге. Они имеют равные начальный и конечный углы, как дуги окружности, но могут быть на любом расстоянии от центра круга.
- Сегменты — это дуги, которые являются частью окружности или круга и имеют начальный и конечный углы, которые не равны 360 градусам.
В зависимости от конкретного контекста могут быть и другие типы дуг, но основные типы – это дуги окружности и произвольные дуги.
В чем разница между градусом от радианом?
Градусы и радианы — это единицы измерения угла. Они могут использоваться для измерения углов различных фигур, таких как треугольники, прямоугольники, круги и другие.
Градус — это одна из самых распространенных единиц измерения угла. Он определяется как 1/360 часть полного угла, который составляет один оборот. Таким образом, полный угол равен 360 градусам.
Радиан — это другая единица измерения угла, которая используется в математике и физике. Радиан определяется как длина дуги, равной радиусу окружности, разделенная на радиус этой окружности. Таким образом, полный угол равен 2π радианам.
Отличие между градусами и радианами заключается в том, как они измеряют углы. Градусы измеряют углы в сотнях долей полного угла, а радианы измеряют углы в длинах дуг окружности.
В математике и физике часто используются радианы, так как они позволяют производить более точные вычисления.
❓ Вопросы и ответы
Некоторые из популярных вопросов и ответы на них по калькулятору длины дуги.
Что такое длина дуги?
Длина дуги — это длина части кривой линии, которая соединяет две заданные точки на кривой.
В каких областях применяется вычисление длины дуги?
Вычисление длины дуги находит применение в различных областях, таких как физика, инженерия, компьютерная графика, дизайн и другие. Например, при моделировании траекторий движения тел, в оптике для расчета оптических путей лучей, при создании графических объектов и многих других задачах.
Как перевести угол из градусов в радианы?
Для перевода угла из градусов в радианы используется следующая формула: θ (в радианах) = θ (в градусах) * π / 180, где π – число Пи (3.14159…).
Какой формат ввода углов используется в калькуляторе длины дуги?
Калькулятор длины дуги использует радианы и градусы для ввода углов.
Какой диапазон углов может быть введен в калькулятор длины дуги?
Углы могут быть введены в диапазоне от 0 до 2π (двух пи), что соответствует полной окружности.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии

{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.

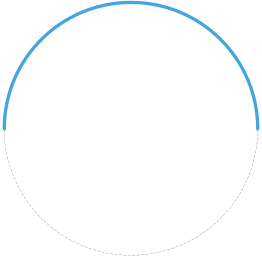
-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
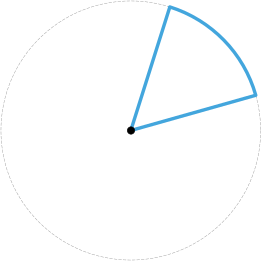
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
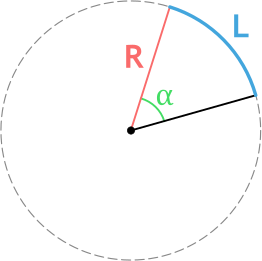
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
Формула длины дуги окружности по формуле Гюйгенса
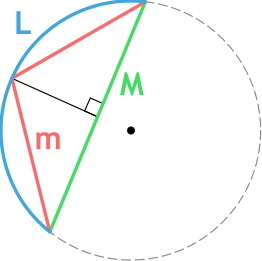
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
Вписанный и центральный угол окружности — коротко о главном
Центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.
Радиус – отрезок, соединяющий центр и точку на окружности.
Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.
Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.
А вот что получится, если соединить две точки на окружности? Тоже отрезок? Так вот, этот отрезок называется «хорда».
Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда ( displaystyle AB) стягивает дугу ( displaystyle AB).
А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».
Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же,
Радиус равен половине диаметра.
Кроме хорд бывают еще и секущие.
Вспомнили самое простое?
А теперь – названия для углов.
Центральный угол – угол между двумя радиусами.
Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.
А теперь – вписанный угол.
Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
При этом говорят, что вписанный угол ( displaystyle ABC) опирается на дугу (или на хорду) ( displaystyle AC).
Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.
Смотри на картинку:
Измерение дуг и углов окружности
Длина окружности. Дуги и углы измеряются в градусах и радианах.
Сперва о градусах
Для углов проблем нет – нужно научиться измерять дугу в градусах.
Градусная мера (величина дуги) – это величина (в градусах) соответствующего центрального угла
Что здесь значит слово «соответствующего»? Смотрим внимательно:
Видишь две дуги ( displaystyle AB) и два центральных угла?
Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше ( displaystyle 180{}^circ )), а меньшей дуге соответствует меньший угол.
Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.
А теперь о радианах
Что же это за зверь такой «радиан»?
Представь себе: радианы – это способ измерения угла … в радиусах!
Угол величиной ( displaystyle 1) радиан – такой центральный угол, длина дуги которого равна радиусу окружности.
Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?
Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?
Этим вопросом задавались учёные ещё в Древней Греции.
И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде ( displaystyle 1,text{ }2,text{ }3,frac{7}{5},frac{2}{239}) и т.п.
И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в ( displaystyle 2,5) раза или в ( displaystyle sqrt{17}) раз больше радиуса!
Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву ( displaystyle pi ).
Итак, ( displaystyle pi ) – это число, выражающее отношение длины полуокружности к радиусу.
Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём ( displaystyle pi ) радиан. Именно оттого, что половина окружности в ( displaystyle pi ) раз больше радиуса.
Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число ( displaystyle pi ), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что
( displaystyle pi approx 3,14)
Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна ( displaystyle 6,28), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква ( displaystyle pi ).
И тогда эта длина окружности окажется равной ( displaystyle 2pi ). И конечно, длина окружности радиуса ( displaystyle R) равна ( displaystyle 2pi R).
Вернёмся к радианам.
Мы выяснили уже, что в развёрнутом угле содержится ( displaystyle pi ) радиан.
Исходя из этого, можно пересчитать любые углы «в градусах» на углы «в радианах». Для этого нужно просто решить пропорцию! Давай попробуем. Возьмём угол в ( displaystyle 30{}^circ ).
Что имеем:
( displaystyle 180{}^circ -pi ) рад.
( displaystyle 30{}^circ – x) рад.
Значит, ( displaystyle x=frac{30{}^circ text{ }!!pi!!text{ }}{180{}^circ }=frac{text{ }!!pi!!text{ }}{6})рад., то есть ( displaystyle 30{}^circ =frac{pi }{6})рад. Таким же образом получается табличка с наиболее популярными углами.
| ( displaystyle 30{}^circ) | ( displaystyle frac{pi }{6}) |
| ( displaystyle 45{}^circ) | ( displaystyle frac{pi }{4}) |
| ( displaystyle 90{}^circ) | ( displaystyle frac{pi }{2}) |
| ( displaystyle 180{}^circ) | ( displaystyle pi ) |
| ( displaystyle 270{}^circ) | ( displaystyle frac{3pi }{2}) |
| ( displaystyle 360{}^circ) | ( displaystyle 2pi ) |
Итак, осознай и не бойся: если ты видишь букву или выражение ( displaystyle frac{7pi }{2}) и т.п., то речь идёт об угле и, по сути, запись через букву ( displaystyle pi) всегда выражает, какую часть от развёрнутого угла составляет тот угол, о котором идёт речь.
А для убедительности ещё раз взгляни на табличку:
| ( displaystyle 30{}^circ) | ( displaystyle frac{pi }{6}) | ( displaystyle frac{1}{6}) от ( displaystyle 180{}^circ ), то есть от ( displaystyle pi ) |
| ( displaystyle 45{}^circ) | ( displaystyle frac{pi }{4}) | ( displaystyle frac{1}{4}) от ( displaystyle 180{}^circ ), то есть от ( displaystyle pi ) |
| ( displaystyle 90{}^circ) | ( displaystyle frac{pi }{2}) | ( displaystyle frac{1}{2}) от ( displaystyle 180{}^circ ), то есть от ( displaystyle pi ) |
| ( displaystyle 180{}^circ) | ( displaystyle pi ) | это и есть ( displaystyle pi ) |
| ( displaystyle 270{}^circ) | ( displaystyle frac{3pi }{2}) | ( displaystyle 270{}^circ ) в ( displaystyle 1,5) раза больше, чем ( displaystyle 180{}^circ ) |
| ( displaystyle 360{}^circ) | ( displaystyle 2pi ) | А это ( displaystyle 2) раза по ( displaystyle 180{}^circ ), то есть ( displaystyle 2pi ) |
