Как найди значения сумм по натуральному ряду

Тема урока: «Сложение с помощью натурального ряда чисел»

Класс: 1

Программа: Развивающая система обучения Л.В.Занкова

Учебник: И.И.Аргинская. Е.П.Бененсон, Л.С.Итина, С.Н.Кормишина «Математика 1 класс. 1 часть», ИД «Фёдоров», 2012 г.

Тип урока: урок изучения нового материала в 1 классе по теме «Сложение и вычитание»

Форма урока: традиционный урок

Цель урока: формирование представлений о разных способах сложения, среди которых выделяется удобный способ сложения чисел.

Задачи урока:

Обучающие: (лежат в области базовой учебной дисциплины):

1. Рассмотреть способ сложения чисел с помощью натурального ряда чисел.

2. Формировать умение выделять информацию из текста и рисунка.

Развивающие:

1. Развитие пространственного мышления.

2. Обогащение речи школьника.

3. Развитие умения давать самооценку своей деятельности.

Воспитательные (детерминируются образовательно-воспитательной парадигмой):

1. Воспитание нравственных качеств.

2. Привитие интереса к урокам математики.

Планируемые результаты

Личностные универсальные учебные действия: интерес к учебному материалу, уважение к мыслям и настроениям другого человека.

Регулятивные универсальные учебные действия: принимать учебную задачу, соответствующую этапу обучения, проговаривать вслух последовательность производимых действий, составляющих основу осваиваемой деятельности, в сотрудничестве с учителем находить варианты решения учебной задачи.

Познавательные универсальные учебные действия: строить небольшие математические сообщения в устной форме, строить рассуждения о доступных наглядно воспринимаемых математических отношениях, выделять несколько существенных признаков объектов.

Коммуникативные универсальные учебные действия: принимать участие в работе парами, следить за действиями других участников учебной деятельности, воспринимать различные точки зрения.

Методы контроля:

• Устный

• Самоконтроль

Оборудование

• Учебник «Математика 1 класс. 1 часть» под редакцией И.И.Аргинской, Е.П.Бененсон, Л.С.Итиной, С.Н. Кормишиной ИД «Фёдоров», 2012 г.

• Мультимедийный проектор

Структура урока

1. Психологическая установка на урок – 2 минуты

2. Актуализация знаний – 8 минут

3. Постановка учебной задачи – 6 минут

4. Применение теоретических положений в условиях выполнения упражнений – 5 минут

5. Динамическая пауза – 2 минуты

6. Обобщение усвоенного и включение его в систему ранее усвоенных знаний – 13 минут

7. Итог урока – 2 минуты

8. Рефлексия – 2 минуты

Этап урока	Ход урока. Содержание.	Время	Обоснование
1. Психологическая установка на урок	– Прозвенел звонок, начинается урок. Итак, сядьте удобно, закройте глаза. Повторяйте за мной: Я в школе на уроке. Сейчас я начну учиться. Я радуюсь этому. Память моя крепка. Я готов к работе. Я работаю!!!	2	Цель: включение учащихся в деятельность на личностно-значимом уровне. На данном этапе я организую положительное самоопределение ученика к деятельности на уроке. Данный этап включает в себя следующие приемы: в начале урока высказываю добрые пожелания детям; предлагаю пожелать друг другу удачи; предлагаю детям девиз «С малой удачи начинается большой успех».
2.Актуализация знаний	Рассмотрите внимательно на рисунок. Что на нем изображено? Я вижу «лишнюю» фигуру. Назовите её. Молодцы! Вы нашли не одно решения, а несколько. Вы были очень внимательными. Что вы можете сказать о чертежах в задании № 241? (Полное совпадение по размеру, цвету фигур, закономерности расположения в ряду). В чём вы заметили разницу? (Круг начерчен при помощи кривой линии, а треугольник – с помощью ломаной линии) Сколько клеток составляет высота фигур? Какие карандаши вам нужны для работы? Перечертите образец из учебника в тетрадь. Раскрасьте первый чертёж так, чтобы треугольник находился за кругом. Теперь раскрасить надо второй чертёж таким образом, чтобы треугольник находился перед кругом. Подумайте, и скажите, можно ли расставить фигуры так, чтобы они закрашивались полностью? Попробуйте фигуры расположить таким образом, чтобы у каждой из них закрашивалась только часть фигуры.	8	Цель: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося. Данный этап предполагает подготовку мышления детей к проектировочной деятельности: 1) актуализацию знаний, умений и навыков, достаточных для построения нового способа действий; 2) тренировку соответствующих мыслительных операций. Этап подразумевает возникновение проблемной ситуации. Задание направлено на развитие умения классифицировать объекты по существенным признакам. Ученики рассуждают: – на рисунке изображены фигуры – геометрические фигуры – треугольники и квадрат – они разного цвета и размера. Рассуждения учеников: – я думаю, что «лишним» будет квадрат, потому что у этой фигуры четыре угла и четыре стороны, а у остальных только три; – я думаю, что красный треугольник, потому что остальные зелёного цвета; – я считаю, что «лишним» будет маленький треугольник, потому что остальные – большие фигуры. Задание способствует формированию пространственного воображения, развивает внимание, умение анализировать. На наборное полотно выставляется голубой круг и красный треугольник. Ученик выходит к доске и располагает треугольник так, что часть его прячется за круг. Остальные ученики внимательно рассматривают расположение фигур на наборном полотне, выясняют, с какой фигуры лучше начать раскрашивание, какая из фигур раскрашивается полностью, а в какой только её часть, и выполняют задание. Повторяется разбор чертежа у доски, выставляется образец, и ученики заканчивают работу самостоятельно. Ученики не находят такого способа и приходят к такому выводу: обязательно одна фигура должна закрывать другую, чтобы у второй фигуры была видна только её часть.
3.Постановка учебной задачи	Рассмотрите задание № 240. Незнайка, Кнопочка и Знайка находили значение суммы 5 + 4 разными способами. Объясни, как нашёл значение суммы Незнайка. А Кнопочка? Каким способом складываешь ты? Знайка сказал: «Я нашёл значение суммы, шагая по натуральному ряду чисел, и сделал это вот так: Как вы думаете, какова тема нашего урока? (Будем складывать, используя натуральный ряд чисел) Для чего необходимы разные способы сложения чисел? (Чтобы найти для себя удобный способ)	6	На данном этапе учащиеся соотносят свои действия с используемым способом действий (алгоритмом, понятием и т.д.) Организовываю коммуникативную деятельность учеников по исследованию возникшей проблемной ситуации в форме эвристической беседы. Завершение этапа связано с постановкой цели и формулировкой (или уточнением) темы урока. Использую методы постановки учебной задачи: побуждающий от проблемной ситуации диалог, подводящий к теме диалог. Задание направлено на актуализацию знаний учащихся по выбору способа нахождения значения сумм, помогает проверить умение детей находить значение суммы с помощью движения по натуральному ряду чисел, формирует умение ориентироваться на числовом луче. В учебнике предлагается три варианта: пересчитыванием, присчитыванием, движением по натуральному ряду чисел. Сначала ученики объясняют способы, которыми воспользовались Незнайка и Кнопочка. Для этого ученики рассматривают картинки и дают пояснения. Затем предлагается рассмотреть способ сложения Знайки. Очень подробно даётся объяснение в учебнике, которое следует прочитать и разобрать. После этого ученики сравнивают своё объяснение с данным в учебнике. Выбирают наиболее рациональный способ. Составляется алгоритм нахождения значения суммы при помощи натурального ряда чисел. Алгоритм вычисления 1.Нужно отметить первое слагаемое. 2.Найти второе слагаемое и сделать столько же шагов вправо по натуральному ряду. 3.Число, на котором закончился счёт, и есть значение суммы.
4.Применение теоретических положений в условиях выполнения упражнений	Какую запись называют натуральным рядом чисел? Запишите натуральный ряд чисел в тетради. Рассмотрите задание № 242. Скажите, как можно назвать данные выражения чисел. Прочитайте первую сумму и запишите её в тетрадь. Назовите первое слагаемое и подчеркните его. Назовите второе слагаемое и обведите его в круг карандашом. Расскажите, как вы будете складывать слагаемые при помощи записанного выше натурального ряда чисел.	5	Цель: проговаривание нового знания, запись в виде опорного сигнала. Учащиеся в форме коммуникативного взаимодействия решают типовые задания на новый способ действий с проговариванием установленного алгоритма во внешней речи. При работе с заданием организуется наблюдение за поэтапным получением результата с помощью натурального ряда чисел. Ученики рассуждают так: отмечаем первое слагаемое, затем находим второе слагаемое, на натуральном ряду чисел стрелкой делаем столько шагов, которое обозначает второе слагаемое. Получаем значение суммы. Аналогично разбирают остальные суммы.
5.Динамическая пауза	Мы устали чуточку, отдохнем минуточку. Поворот, наклон, прыжок, Улыбнись давай, дружок. Еще попрыгай: раз, два, три! На соседа посмотри, Руки вверх и тут же вниз И за парту вновь садись!	2	Цель: отдых детей, настрой на следующий этап работы. Применяю здоровьесберегающие технологии
6.Обобщение усвоенного и включение его в систему ранее усвоенных знаний	А) Послушайте внимательно следующее задание: Сколько детей собирали пирамидки? Назовите их имена. Сколько девочек и мальчиков играли? Кого больше? Где чья пирамидка? Чем отличаются пирамидки у детей? У кого в пирамидке больше всего разных цветов? Назовите эти цвета. Сколько колец в пирамидке у Даши? А у мальчиков? У кого из детей самая узкая пирамидка? Как изменить пирамидки мальчиков, чтобы они сравнялись по высоте с пирамидкой Даши? Сколько колец добавим Ване? Какого цвета будут следующие три кольца, чтобы закономерность в цвете не изменилась? Как вы рассуждали? Какое выражение можно записать? Найдите значение суммы, используя натуральный ряд чисел. Сравните два равенства. Что вы можете о них сказать? 5 + 3 = 8 6 + 2 = 8 Как изменить пирамидки Даши и Вани, чтобы они стали равными по высоте с пирамидкой Миши? Какие два способа уравнивания количества колец в разных пирамидах мы с вами нашли? Чем эти способы отличаются друг от друга? Можно ли с числами выполнять другие действия, кроме сложения? Можете ли вы их назвать?	7	Цель: каждый для себя должен сделать вывод о том, что он уже умеет. При проведении данного этапа используется парная форма работы. Эмоциональная направленность этапа состоит в организации ситуации успеха, способствующей включению учащихся в дальнейшую познавательную деятельность. Задание способствует развитию логического мышления, наблюдательности, быстроты реакции, интереса к усвоению математических знаний и зависимостей, формированию поисковых подходов к решению любой задачи в работе парами. Ученики внимательно рассматривают рисунки, парами обсуждают решение задачи. Дальше проводится коллективное обсуждение рисунка. Ученики рассуждают так: если Даша собирала самую высокую пирамидку, а у Маши была самая узкая, то получается, что у Вани была самая низкая пирамидка, на рисунке она первая. Нужно добавить недостающее число колец каждому мальчику. Ученики рассуждают: Ване надо добавить 3 кольца – красное, белое, красное. Можно записать следующее выражение: 5 + 3. Аналогично выясняется количество колец, которые нужно добавить Мише, обсуждается цвет колец, составляется сумма чисел. Ученики приходят к выводу: Ване надо добавить одно кольцо, а у Даши убрать два.
	Б) Посмотрите на рисунок в задании № 243. Кого изобразил художник? А кто спрятался в камышах? Составьте по рисунку разные математические рассказы. Что мы можем узнать? Какой математический знак поможет нам узнать, сколько стало утят? Как называется выражение, в котором между числами стоит знак сложения? Составьте по этому рассказу сумму чисел. Составьте ещё один рассказ. Что мы можем узнать из рассказа? Составьте новую сумму чисел. Сравните записанные равенства и сделайте вывод.	6	Задание направлено на закрепление знаний, умений и навыков правильно и быстро выполнять действия с числами первого десятка, развитие математической речи, закрепление правила о зависимости суммы от перестановки слагаемых. Первый рассказ: На озере в камышах было 4 утёнка. К ним пришли ещё 3 утёнка. Ученики рассуждают: если утята объединились, то можем узнать, сколько их стало. Сумма чисел 4 + 3 составляется с помощью карточек на наборном полотне и записывается в тетрадь. Находится значение суммы по натуральному ряду чисел. Второй рассказ: Три утёнка пришли на озеро купаться, а там уже в камышах было 4 их товарища. Ученики составляют сумму 3 + 4, записывают её в тетрадь и находят значение по натуральному ряду чисел. Ученики рассуждают: в равенствах слагаемые поменялись местами, но значение суммы осталось неизменным. Здесь применили правило: от перестановки мест слагаемых значение суммы не меняется.
7.Итог урока	Какую задачу ставили? Удалось решить поставленную задачу? Какие получили результаты? Где можно применить новое знание? Что на уроке у вас хорошо получалось? Над чем еще надо поработать?	2	Цель: осознание учащимися своей учебной деятельности, самооценка результатов деятельности своей и всего класса.
8.Рефлексия		2	Цель: каждый для себя должен сделать вывод о том, что он уже умеет.

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} – frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} – frac{1}{2n+1} + frac{1}{2n+1} – frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$

I. Повторение изученного.

1. Чистописание.

На доске чертеж.

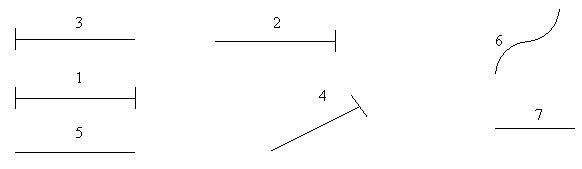
– Рассмотри чертеж (рис. 1).

– Найди на нем все отрезки и запиши их номера в
тетради.

– Найди лучи и запиши их номера на следующей
строке.

– Заполни строчки цифрами.

– Как называются те линии, номера которых вы не
выписали?

– 5 и 7 – прямые линии;

– 6 – кривая линия.

– Как проверить, прямая или кривая линия?

– Для проверки, прямая это линия или кривая,
нужно приложить линейку.

2. На доске запись: 5   7   9
   4   6   3   8   2.

– Я показываю число, вы называете следующее
(назвать следующее число).

– Как вам удается так быстро выполнять задание?

– Знаем порядок счета.

– Знаем, какое число за ним следует.

– Умеем прибавлять 1.

– Умеем пользоваться числовым рядом и т.д.

– Найди среди этих чисел самое большое и самое
маленькое число.

Варианты вопросов учителя:

– Я видела, некоторые из вас смотрели вот сюда
(показывает на числовой ряд). Зачем?

– Какое действие вы выполняли, чтобы назвать
следующее число? (Действие сложения.)

– И сколько же вы прибавили? (Прибавляли по
одному.)

– Почему? (Потому что в числовом ряду каждое
следующее число на 1 больше.)

– Сравни эти числа с помощью рисунка.

(Дети рисуют на первой строчке 9 кружков, а на
второй 2 кружка.)

Соединяя парами кружки первого и второго ряда,
ученики приходят к выводу, что 9 больше 2 на 7 и 2
меньше 9 тоже на 7, так как 7 кружков остались без
пары.

В тетради записывают неравенство: 9>2 и 2<9.

3. Использование числового ряда при
отсчитывании 1. (Работа строится аналогично и с
теми же числами.)

– Можно ли назвать данные числа натуральным
рядом чисел?

– Нет, потому что они стоят вперемежку.

– Расположи числа в порядке увеличения, а потом
в порядке уменьшения.

2   3   4   5   6
   7   8   9   9   8
   7   6   5   4   3
   2

– Что мы с вами получили?

(1 – отрезок натурального ряда чисел, 2 – ряд
чисел.)

–Почему первый ряд называется отрезком
натурального ряда чисел?

– Первый отрезок начинается с 2 и кончается
числом 9.

– Как превратить отрезок натурального ряда
чисел в натуральный ряд чисел?

– Перед числом 2 надо написать 1, так как
натуральный ряд чисел начинается с 1, и каждое
следующее число больше предыдущего на 1. После 9
надо поставить многоточие, которое обозначает,
что дальше есть еще числа натурального ряда, но
они не записаны.

– На какие геометрические фигуры похожи
натуральный ряд и отрезок натурального ряда
чисел?

– Натуральный ряд чисел похож на луч, у
которого есть начало, но нет конца. Отрезок
натурального ряда чисел похож на отрезок. Оба
имеют начало и конец.

4. На доске записаны числа по парам:

4   5   1   3   2   
6   6   3

– Поставь между числами знаки сравнения:

– Как называются получившиеся выражения?

– Неравенства.

– Сделай рисунок к первому и последнему
неравенствам.

(Дети в тетрадях рисуют.)

– Напишите еще несколько неравенств.

(После выполнения задания коллективно
проверяется правильность постановки знаков.)

Физкультминутка.

II. Работа над новым материалом.

– На доске написаны числа по парам:

3   4   6   2   5
   4   3   9

– Какие задания можно выполнить с этими
числами?

– Можно их сравнить.

– Можно нарисовать кружочки и сравнить.

– С некоторыми из них можно составить отрезок
натурального ряда чисел.

– Поставь между числами знак “+”.

– Что значит запись 3+4 ?

– Эта запись называется сумма.

– Сделайте рисунок и напишите, сколько
получилось при сложении?

– Почему между суммой и числом 7 стоит знак
равенства?

– Левая часть равна правой части.

Вывод: число 7 – значение суммы 3 + 4.

– Запиши еще четыре суммы и найди их значения,
используя палочки.

– Подчеркни суммы чисел синим цветом, значение
суммы – красным.

III. Работа по учебнику.

1. Выполняют задание № 79, стр. 34.

Раскрашивают: там, где значение суммы равно 9, –
зеленым цветом, там где 6 – черным цветом, 8 –
желтым, 7 – серым цветом.

– Какие фигуры животных появились на ваших
рисунках?

(Должны появиться фигуры кошки, собаки.)

IV. Закрепление.

1. Сравнение сумм с числами.

6 + 2       8

6 + 2       7

6 + 2       9

– Поставь знаки сравнения. Проверь рисунками.

Учитель предлагает подумать, как сравнить не
число с числом, а сумму с числом.

Дети сами догадаются, что нужно найти значение
суммы и сравнить с числом.

Важно, чтобы ученики заметили, что слева стоит
одна и та же сумма, значит, достаточно найти ее
значение один раз.

Найти значение суммы лучше всего, пользуясь
натуральным рядом чисел.

1 2 3 4 5 6 7 8 9 …    6 + 2 = 8

Значит:
6 + 2 = 8

6 + 2 > 7

6 + 2 < 9

– Как можно еще проверить правильность
выполнения задания?

Дети свое решение проверяют с помощью рисунков.

2. Самостоятельная работа.

Даны 3 линейки разной длины: первая имеет 9
делений, вторая –7 делений, третья – 8 делений.

Раскрасить линейки, если зеленая линейка
длиннее красной, а красная длиннее желтой.

(Первая – зеленого цвета, вторая – желтого,
третья – красного цвета.)

V. Итог урока.

Экспресс–опрос.

В тетради дети записывают ряд чисел от 1 до 7.

Затем учитель читает свои утверждения, а дети
под соответствующим номером отмечают свое
согласие или несогласие с помощью знаков “+” и
“–”.

При чтении утверждений 1–3 учитель указкой
показывает записанные на доске числа. Затем он
сознательно убирает указку, активизируя детей
самостоятельно обращаться к записанному ряду
чисел.

Запись на доске:

3   4   5   6   7
   8   9

Задания для экспресс–опроса:

1. На доске записан числовой ряд.

2. Числа записаны в порядке убывания.

3. Каждое последующее число больше предыдущего
на 1.

4. Перед числом 7 в числовом ряду стоит число 9.

5. Значение суммы чисел 2 и 2 равно 4.

6. Прямая линия не имеет ни начала, ни конца.

7. Этот ряд чисел можно продолжить.

В тетрадях должна быть следующая запись:

1 2 3 4 5 6 7

– – + – + + +

Проверка. Дети в парах обмениваются тетрадями.

Экспресс–опрос позволяет учителю быстро
проверить степень усвоения пройденного
материала по определенной теме.

Всем привет! Добро пожаловать на канал любителей математики! Сегодня Вас ждёт увлекательная тема.

Большинство из нас в старших классах школы или другом учебном заведении изучали пределы. О них мы ещё как-нибудь поговорим подробнее. При их изучении мы сталкивались с таким понятием, как бесконечность. Понятие это довольно абстрактное, но, тем не менее, в математике оно используется нередко. Главное, понять его суть. Бесконечность – это то, что никогда не прекратит увеличиваться (или уменьшаться, если говорить о минус бесконечности). Как только Вы где-то остановитесь, это уже будет не бесконечность. Это, скорее всего, будет какое-то колоссальное число больше гугола или даже гуголплекса. Слышали про такие числа? Если нет, то гугол – это 10 в степени 100, а гуголплекс – это 10 в степени гугол )) Так вот, бесконечность, важно понять, – это не какое-то очень большое число, это идея. Но с этой идеей можно работать. Это была предыстория к сегодняшней теме ))

Вы когда-нибудь задумывались о том, что получится, если сложить все натуральные числа? 1+2+3+4+5+…=? Сколько это будет? Бесконечность? Бесконечность в степени бесконечность? Как найти или оценить эту сумму? Ответ на этот вопрос, как Вы увидите, абсолютно неочевиден. Более того, он большинству покажется бредом)) Тем не менее это факт. Который, кстати, используется в некоторых областях физики: в частности, в квантовой механике и теории струн.

Существует несколько способов для нахождения суммы всех натуральных чисел. Например, через дзета-функцию и эта-функцию Дирихле. Но это относится к области математического анализа и для большинства будет очень сложно в понимании. Но есть и довольно простой и наглядный способ показать, как найти эту сумму, не углубляясь при этом в глубины матанализа.

Для того, чтобы найти сумму всех натуральных чисел, нам понадобятся два других вспомогательных бесконечных ряда чисел, точнее их сумма. Первый ряд – это так называемый ряд Гранди, и выглядит он так: 1-1+1-1+1-1+1… и т. д. Второй ряд выглядит так: 1-2+3-4+5-6+7… Он ещё называется знакочередующийся натуральный ряд. Если мы найдём суммы этих двух рядов, то этого будет достаточно, чтобы найти сумму ряда всех натуральных чисел.

Найдём сумму первого ряда:

Почему сумма равна 1/2? Всё просто: если остановиться на нечётном члене ряда, сумма получится равной 1, если на чётном – 0. Поскольку ряд бесконечен, то берётся среднее значение от 0 и 1. Это равно 1/2.

Теперь разберёмся с суммой знакочередующегося натурального ряда.

Для того, чтобы найти сумму ряда, находится его удвоенное значение. Для этого складываем два одинаковых ряда столбиком, но второй сдвигаем относительно первого вправо на один член. Складывая почленно, получим, что удвоенная сумма второго ряда равна сумме ряда Гранди, т. е. 1/2. Тогда сумма знакочередующегося ряда равна половине суммы ряда Гранди, т. е. 1/4.

Что ж, мы нашли суммы вспомогательных рядов. Теперь мы сможем найти сумму всех натуральных чисел.

Для того, чтобы найти искомую сумму, вычтем из неё ряд № 2, сумму которого мы нашли ранее. Вычитая столбиком почленно получаем, что разность нечётных членов равна 0, а чётных: 4, 8, 12, и т. д. Тогда если из полученной суммы вынести за скобку 4, получим, что в скобке остаётся сумма того же ряда всех натуральных чисел. Получится уравнение с одной неизвестной. Решая его, находим, что сумма всех натуральных чисел равна -1/12. Как я и говорил в самом начале, ответ получился абсолютно неочевидным, пожалуй, даже безумным! Но это на самом деле так ))

Теперь Вы можете, спрашивая у Ваших друзей, чему равна сумма всех натуральных чисел, приводить им ответ, который вызывает просто взрыв мозга! ))) Причём, Вы сможете это доказать!

Надеюсь, друзья, Вам понравилась статья. Буду благодарен за лайки, комментарии и подписки.

P.S. Хотите напоследок интересную задачку из древности? Она должна Вам понравиться. Вот она. Летела стая гусей. Навстречу ей – один гусь. «Здравствуйте, сто гусей», – говорит он им. Вожак отвечает: «Нас не сто гусей; вот если бы нас было столько, сколько сейчас, да ещё столько, да ещё полстолька, да ещё четвертьстолька, да ещё ты, гусь, с нами, вот тогда нас было бы сто гусей». Сколько гусей летело в стае? Ответ будет в конце следующей статьи.

Предыдущая статья

Следующая статья

Эта статья — о числовом ряде 1 + 2 + 3 + 4 + …. О последовательности натуральных чисел — 1, 2, 3, 4, … — см. Натуральное число.

Ряд из натуральных чисел — числовой ряд (бесконечная сумма элементов), членами которого являются последовательные натуральные числа: ; при этом n-я частичная сумма ряда является треугольным числом:

которое неограниченно растёт при стремлении к бесконечности. Из-за того, что последовательность частичных сумм ряда не имеет конечного предела, ряд расходится, то есть не имеет конечной суммы.

Из-за расходимости ряд не имеет никакой значимой ценности для традиционных математических подходов. Но при некотором уровне манипулирования можно получить нетривиальные результаты, находящие применение в комплексном анализе, квантовой теории поля^{[источник не указан 1729 дней]} и теории струн^[1].

Специальные методы суммирования[править | править код]

В математике существуют методы суммирования, которые позволяют присвоить определённые числовые значения (конечные) даже расходящимся рядам. Одним из таких способов является метод, основанный на регуляризации аналитического продолжения дзета-функции Римана. Другим популярным вариантом является суммирование по методу Рамануджана^[en][2]. Многие из подобных методов присваивают ряду одинаковое значение в виде отрицательной дроби:

Частичные суммы[править | править код]

Частичными суммами натурального ряда являются 1, 3, 6, 10, 15 и т. д. Таким образом, n-я частичная сумма выражается формулой

Это выражение было известно ещё Пифагору в VI веке до нашей эры^[3]. Числа такого вида называются треугольными, так как они могут быть представлены в виде треугольника.

Бесконечная последовательность треугольных чисел стремится к и, следовательно, бесконечная сумма натурального ряда также стремится к . Такой результат является следствием невыполнения необходимого условия сходимости числового ряда.

Суммируемость[править | править код]

В сравнении с другими классическими расходящимися рядами, натуральному ряду сложнее приписать имеющее смысл некоторое конечное числовое значение. Существует множество методов суммирования, некоторые из которых являются более устойчивыми и мощными. Так, например, суммирование по Чезаро является широко известным методом, который суммирует умеренно расходящийся ряд Гранди 1 − 1 + 1 − 1 + … и приписывает ему конечное значение 1/2. Суммирование методом Абеля представляет собой более мощный метод, который, кроме ряда Гранди, позволяет также суммировать более сложный знакочередующийся ряд натуральных чисел и присвоить ему значение 1/4.

В отличие от упомянутых выше рядов, как суммирование по Чезаро, так и метод Абеля неприменимы к натуральному ряду. Эти методы работают только со сходящимися и гармоническими рядами и не могут быть использованы для ряда, частичные суммы которого стремятся к +∞^[4]. Большинство элементарных определений суммы расходящегося ряда являются линейными и устойчивыми, а любой линейный и устойчивый метод не может присвоить натуральному ряду конечное значение.

Следовательно, для этого случая возможно применение только специальных методов, таких как регуляризация дзета-функцией или суммирование Рамануджана.

Эвристические предпосылки[править | править код]

В главе 8 первого сборника своих трудов Рамануджан показал, что «1 + 2 + 3 + 4 + … = −1/12», используя два способа^[5][6][7]. Ниже излагается более простой метод, состоящий из двух этапов.

Первое ключевое наблюдение состоит в том, что ряд 1 + 2 + 3 + 4 + … похож на знакочередующийся ряд натуральных чисел 1 − 2 + 3 − 4 + …. Несмотря на то, что этот ряд также является расходящимся, с ним намного проще работать. Существует несколько классических способов присвоить конечное значение этому ряду, известных ещё с XVIII века.^[8]

Для того, чтобы привести ряд 1 + 2 + 3 + 4 + … к виду 1 − 2 + 3 − 4 + …, мы можем вычесть 4 из второго члена, 8 из четвёртого члена, 12 из шестого и т. д. Общая величина, которую нужно вычесть, выражается рядом 4 + 8 + 12 + 16 + …, который получается умножением исходного ряда 1 + 2 + 3 + 4 + … на 4. Эти выражения можно записать в алгебраической форме. Что бы из себя ни представляла «сумма», введём для неё обозначение c = 1 + 2 + 3 + 4 + …, умножим полученное уравнение на 4 и вычтем второе из первого:

Второе ключевое наблюдение заключается в том, что ряд 1 − 2 + 3 − 4 + … является разложением в степенной ряд функции 1/(1 + x)² при x, равном 1. Соответственно, Рамануджан заключает:

Поделив обе части на −3, получаем c = −1/12.

Строго говоря, существует неоднозначность при работе с бесконечными рядами в случае использования методов, предназначенных для конечных сумм (наподобие тех методов, что были использованы выше), в особенности если эти бесконечные ряды расходятся. Неоднозначность заключается в том, что если вставить ноль в любое место в расходящемся ряде, существует вероятность получить противоречивый результат. Например, действие 4c = 0 + 4 + 0 + 8 + … противоречит свойствам сложения.

Одним из способов обойти эту неопределённость и тем самым ограничить позиции, куда можно вставить ноль, является присвоение каждому члену ряда значения некоторой функции.^[9] Для ряда 1 + 2 + 3 + 4 + …, каждый член n представляет собой натуральное число, которое может быть представлено в виде функции n^−s, где s — некоторая комплексная переменная. Используя такое представление, можно гарантировать, что все члены ряда последовательны. Таким образом, присвоив s значение −1, можно выразить рассматриваемый ряд в строгом виде. Реализация этого способа носит название регуляризации дзета-функцией.

Регуляризация дзета-функцией[править | править код]

В этом методе, ряд заменяется рядом . Последний ряд является частным случаем ряда Дирихле. Если действительная часть s больше 1, ряд Дирихле сходится, и его сумма представляет собой дзета-функцию Римана ζ(s). С другой стороны, если действительная часть s меньше или равна 1, ряд Дирихле расходится. В частности, ряд 1 + 2 + 3 + 4 + …, который получается подстановкой s = −1, не является сходящимся. Преимущества перехода к дзета-функции Римана заключается в том, что, используя метод аналитического продолжения, она может быть определена для s ⩽ 1. Следовательно, мы можем получить значение регуляризованной дзета-функции ζ(−1) = −1/12.

Существует несколько способов доказать, что ζ(−1) = −1/12. Один из методов^[10] использует связь между дзета-функцией Римана и эта-функцей Дирихле^[en] η(s). Эта-функция выражается знакопеременным рядом Дирихле, согласуясь тем самым с ранее представленными эвристическими предпосылками. Тогда как оба ряда Дирихле сходятся, следующие тождества верны:

Тождество остаётся справедливым если мы продолжим обе функции аналитически в область значений s, где вышезаписанные ряды расходятся. Подставляя s = −1, получим −3ζ(−1) = η(−1). Отметим, что вычисление η(−1) является более простой задачей, так как значение эта-функции выражается значением суммы Абеля соответствующего ряда^[11] и представляет собой односторонний предел:

Поделив обе части выражения на −3, получаем ζ(−1) = −1/12.

Суммирование методом Рамануджана[править | править код]

Суммирование ряда 1 + 2 + 3 + 4 + … методом Рамануджана также позволяет получить значение −1/12. В своём втором письме к Х. Г. Харди, датированном 27 Февраля 1913, Рамануджан пишет^[12]:

Уважаемый Сэр, я с большим удовольствием прочёл ваше письмо от 8 февраля 1913 года. Я ожидал, что вы ответите мне в том же стиле, что и профессор математики из Лондона, который посоветовал мне внимательно изучить «Бесконечные ряды» Томаса Бромвича и не попадать в ловушку, которую таят расходящиеся ряды. … Я ответил ему, что, согласно моей теории, сумма бесконечного числа членов ряда 1 + 2 + 3 + 4 + … = −1/12. Узнав это, вы сию же минуту укажете в направлении психиатрической лечебницы. Уверяю, вы не сможете проследить нить рассуждений в моём доказательстве этого факта, если я попытаюсь изложить их в единственном письме.

Метод суммирования Рамануджана заключается в изолировании постоянного члена в формуле Эйлера — Маклорена для частичных сумм ряда. Для некоторой функции f, классическая сумма Рамануджана для ряда определена как

где f^(2k−1) представляет собой (2k−1)-ю производную функции f и B_2k является 2k-м числом Бернулли: B₂ = 1/6, B₄ = −1/30 и т. д. Принимая f(x) = x, первая производная f равна 1, а все остальные члены стремятся к нулю, поэтому:^[13]

Для избежания противоречий современная теория метода суммирования Рамануджана требует, чтобы функция f являлась «регулярной» в том смысле, что её производные высших порядков убывают достаточно быстро для того, чтобы оставшиеся члены в формуле Эйлера — Маклорена стремились к 0.
Рамануджан неявно подразумевал это свойство.^[13] Требование регулярности помогает избежать использования метода суммирования Рамануджана для рядов типа 0 + 2 + 0 + 4 + … потому, что не существует регулярной функции, которая выражалась бы значениями такого ряда. Такой ряд должен интерпретироваться с использованием регуляризации дзета-функцией.

Несостоятельность устойчивых линейных методов суммирования[править | править код]

Линейный и устойчивый метод суммирования не в состоянии присвоить конечное значение ряду 1 + 2 + 3 + … (Устойчивый означает, что добавление члена в начало ряда увеличивает сумму ряда на величину этого члена.) Это утверждение может быть продемонстрировано следующим образом. Если

1 + 2 + 3 + … = x,

тогда, добавляя 0 к обеим частям, получаем

0 + 1 + 2 + … = 0 + x = x,

исходя из свойства устойчивости.
Вычитая нижний ряд из верхнего, получаем

1 + 1 + 1 + … = x − x = 0,

исходя из свойства линейности.
Добавляя 0 к обеим частям повторно, получаем

0 + 1 + 1 + 1 + … = 0

и вычитая два последних ряда, приходим к

1 + 0 + 0 + … = 0,

что противоречит свойству устойчивости.

Методы, использованные выше, для суммирования 1 + 2 + 3 + … являются либо только устойчивыми, либо только линейными. Например, существует два разных метода, называемых регуляризацией дзета-функцией. Первый является устойчивым, но нелинейным и определяет сумму a + b + c + … множества чисел как значение аналитического продолжения выражения 1/a^s + 1/b^s + 1/c^s + при s = −1. Второй метод линейный, но неустойчивый и определяет сумму последовательности чисел как значение аналитического продолжения выражения a/1^s + b/2^s + c/3^s при s = 0. Оба метода присваивают ряду 1 + 2 + 3 + … значение суммы ζ(−1) = −1/12.

Применение в физике[править | править код]

Значение −1/12 встречается в теории бозонных струн при попытке рассчитать возможные энергетические уровни струны, а именно низший энергетический уровень^[1].

Регуляризация ряда 1 + 2 + 3 + 4 + … также встречается при расчёте эффекта Казимира для скалярного поля в одномерном пространстве.^[14] Похожие вычисления возникают для трёхмерного пространства, однако в этом случае вместо дзета-функции Римана используются реальные^{[уточнить]} аналитические ряды Эйзенштейна.^[15]

Примечания[править | править код]

Список литературы[править | править код]

• Berndt, Bruce C., Srinivasa Ramanujan Aiyangar, and Robert A. Rankin. Ramanujan: letters and commentary (неопр.). — American Mathematical Society, 1995. — ISBN 0-8218-0287-9.
• Hardy, G. H. Divergent Series (англ.). — Oxford University Press, 1949.
• Zee, A. Quantum field theory in a nutshell (неопр.). — Princeton UP, 2003. — ISBN 0-691-01019-6.

Ссылки[править | править код]

• This Week’s Finds in Mathematical Physics (Week 124), (Week 126), (Week 147), (Week 213)
  • Euler’s Proof That 1 + 2 + 3 + · · · = −1/12 — By John Baez
  • John Baez. My Favorite Numbers: 24 (19 сентября 2008).
• The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation by Terence Tao
• A recursive evaluation of zeta of negative integers by Luboš Motl
• ASTOUNDING: 1 + 2 + 3 + 4 + 5 + … = −1/12 Numberphile video with over a million views
  • Sum of Natural Numbers (second proof and extra footage) includes demonstration of Euler’s method.
  • What do we get if we sum all the natural numbers? response to comments about video by Tony Padilla
  • Related article from New York TImes
• Divergent Series: why 1 + 2 + 3 + · · · = −1/12 by Brydon Cais from University of Arizona