Как найдите объем куба если известна площадь

Загрузить PDF

Объем трехмерной фигуры является величиной, которая характеризует пространство, занимаемое этой фигурой. Объем равен произведению длины фигуры на ее ширину и на высоту. Куб — это трехмерная фигура, у которой длина, ширина и высота одинаковые, то есть все ребра куба равны.^[1] Поэтому вычислить объем куба довольно просто, если знать значение его ребра. А ребро можно найти по площади поверхности куба.

1
Запишите формулу для вычисления площади поверхности куба. Формула выглядит так: $S=6x^{{2}}$ , где — ребро куба.^[2]
- Чтобы вычислить объем куба, нужно перемножить значения трех его ребер (длину, ширину и высоту).^[3] У куба длина, ширина и высота равны, поэтому нужно найти значение одного (любого) ребра, чтобы вычислить объем куба. Имейте в виду, что для вычисления площади поверхности куба нужно знать значение ребра; поэтому, если площадь поверхности куба дана, вы с легкостью найдете его ребро, а затем вычислите объем куба.
2

В формулу подставьте значение площади поверхности куба. Площадь поверхности должна быть дана в задаче.
3

Разделите значение площади поверхности куба на 6. Так вы найдете значение $x^{{2}}$ .
4

Извлеките квадратный корень. Так вы найдете значение , то есть значение ребра куба.

Реклама

1

Запишите формулу для вычисления объема куба. Формула выглядит так: $V=x^{{3}}$ , где – объем куба, — ребро куба.^[4]
2
В формулу подставьте значение ребра куба. Это значение вы нашли по известной площади поверхности куба.
- Например, если ребро куба равно 4 см, формула запишется так:
  $V=4^{{3}}$ .
3

Возведите в куб (в третью степень) значение ребра куба. Сделайте это на калькуляторе или просто умножьте «x» на себя три раза. Так вы найдете объем куба в кубических единицах измерения.

Реклама

Что вам понадобится

Карандаш/ручка
Бумага

Об этой статье

Эту страницу просматривали 32 956 раз.

Была ли эта статья полезной?

Источник

Как найти объём куба, если известна площадь его полной поверхности?

Последнее редактирование ответа: 09.11.2010

Оставить отзыв

Оставить отзыв

Вы можете написать свои замечания к ответу, предложения об улучшении или просто поблагодарить автора. Комментарий, после проверки, увидят автор и редактор ответа. Будьте, пожалуйста, вежливыми. Спасибо!

Если Вы хотите получить уведомление об
исправлении ответа укажите свой e-mail:

Неправильный формат адреса электронной почты

Объём куба

Главная
/
Математика
/
Геометрия
/
Объём куба

Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Объём куба через ребро

Чему равен объём куба, если:

ребро a =

V_куба =

Округление ответа:

Объём куба через диагональ

Чему равен объём куба, если:

диагональ d =

V_куба =

Округление ответа:

Объём куба через площадь поверхности

Чему равен объём куба, если:

S_пов =

V_куба =

Округление ответа:

Теория

Как найти объём куба зная длину ребра

Чему равен объём куба V_куба, если длина его рёбер a:

Формула

V_куба = a³

Пример

Для примера, найдём объём куба, у которого рёбра a = 5 см:

V_куба = 5³ = 125 см³

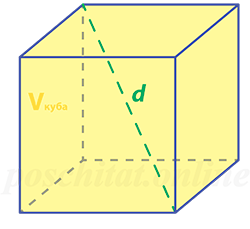
Как найти объём куба зная диагональ

Чему равен объём куба V_куба, если его диагональ d:

Формула

V_куба =^d³ ⁄_3√3

Пример

Для примера, найдём объём куба, длина диагонали которого d = 9 см:

V_куба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³

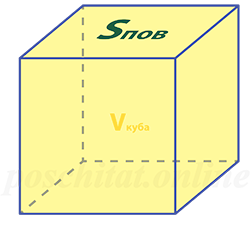
Как найти объём куба зная площадь поверхности

Чему равен объём куба V_куба, если площадь поверхности этого куба S_пов:

Формула

V_куба =^{√S_пов³} ⁄_6√6

Пример

Для примера, найдём объём куба, площадь поверхности которого S_пов = 24 см²:

V_куба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³

См. также

Источник

Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).

Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.

Содержание:

калькулятор объема куба
формула объема куба через ребро
формула объема куба через диагональ грани
формула объема куба через периметр грани
формула объема куба через диагональ куба
формула объема куба через площадь полной поверхности
примеры задач

Формула объёма куба через ребро

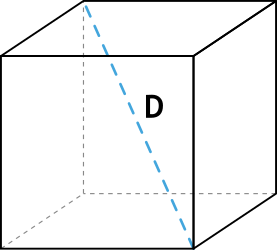
Формула объёма куба через диагональ грани

{V = Big( dfrac{d}{sqrt{2}} Big) ^3}

d – диагональ грани куба

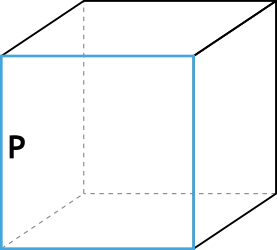
Формула объёма куба через периметр грани

{V= Big( dfrac{P}{4} Big) ^3}

P – периметр грани куба

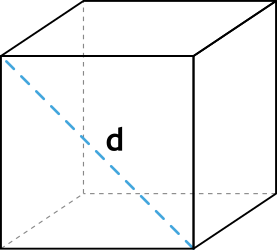
Формула объёма куба через диагональ куба

{V= dfrac{D^3}{3sqrt{3}}}

D – диагональ куба

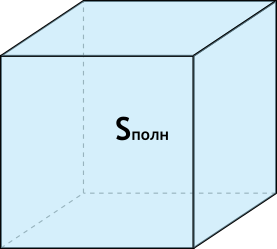
Формула объёма куба через площадь полной поверхности

{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}

S_полн – диагональ куба

Примеры задач на нахождение объема куба

Задача 1

Чему равен объём куба с ребром 5 см?

Решение

Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:

V=a ^ 3 = 5 ^ 3 = 125 : см^3

Ответ: 125 см³

Воспользуемся калькулятором для проверки полученного результата.

Задача 2

Найти объем куба, если площадь его поверхности равна 96 см².

Решение

В данном примере нам подойдет эта формула:

V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3

Ответ: 64 см³

Проверить ответ поможет калькулятор .

Также на нашем сайте вы можете найти объем конуса.

Источник

Download Article

The volume of a three-dimensional shape is a measurement of the space inside the shape and is determined by multiplying the length, width, and height. A cube is a three-dimensional shape in which the length, width, and height are equal. Thus, it is easy to find the volume of a cube given the length of one edge. You can also find the volume using the surface area, from which you can derive the length of one edge.

1
Set up the formula for the surface area of a cube. The formula is $surfacearea=6x^{{2}}$ , where equals the length of one edge of the cube.^[1]
- To find the volume of a cube, you need to multiply its three dimensions (length, width, height) together.^[2] These dimensions correspond to the length of the edges of the cube. Since all the dimensions (edges) of a cube are the same, in order to find the volume of the cube, you first have to determine the length of one of its edges. Since finding the surface area of a cube also requires the length of one edge, if you know the surface area, you can work backwards to find the length of one edge, then use the edge length to work forward to find the volume.
2

Plug the surface area of the cube into the formula. This information should be given.

Advertisement
3

Divide the surface area by 6. This will give you the value of $x^{{2}}$ .
4

Find the square root. This will give you the value of , or the length of one edge of the cube.

1

Set up the formula for the volume of a cube. The formula is $v=x^{{3}}$ , where equals the volume of the cube, and equals the length of one edge.^[3]
2
Plug the length of one edge into the formula. You should have already calculated this from the given surface area.
- For example, if one edge of a cube is 4 centimeters, then your formula will look like this:
  $v=4^{{3}}$ .
3

Cube the length of one edge. To do this, you can use a calculator, or simply multiply x by itself three times. This will give you the volume of your cube, in cubic units.^[4]

Add New Question

Question

What about a rectangular prism? Would it still be the same?

Not quite. The formula is slightly different. Assuming you know the length, width and height of the prism (l, w, and h), you would multiply the three values together to get the volume, or you would find twice the sum of (lw + lh + wh) to find the surface area. If you know only two of those values, but you also know either the volume or the surface area, you can work backwards to find the unknown value.
Question

The volume of a cube is 64 mm^3. How do I calculate the area of one of its faces?

The length of an edge is the cube root of 64, which is 4 mm. The face area is 4² = 16 sq mm.
Question

What is the volume of a cube with a surface area of 78 inches?

First you need to find the length of one edge using the formula for surface area:
78 = 6x^2
13 = x^2
3.61 inches = x

Now that you know the length of one edge, you can plug this value into the formula for volume of a cube:
v = 3.61^3
v = 3.61 x 3.61 x 3.61
v = 47.05 cubic inches

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Things You’ll Need

Pencil/pen
Paper

About This Article

Article SummaryX

To find the volume of a cube from its surface area, first use the formula for surface area to find the length of one side of your cube. To do this, plug the surface area you’re given into the formula, which is surface area = 6x^2, where x is the length of one side of the cube. Then, solve for x. You can then find the volume of your cube by using the formula v = x^3 where v is volume and x is the number you got previously for the length of one side of your cube. To see an example of how to find the volume of a cube from its surface area, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 162,714 times.

Did this article help you?

Источник

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Как найти объём куба, если известна площадь его полной поверхности?

Оставить отзыв

Похожие вопросы

Объём куба