Задания
Версия для печати и копирования в MS Word
Тип 2 № 548525 

i
Объем конуса равен 104. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Спрятать решение
Решение.
Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса.
Ответ: 13.
Аналоги к заданию № 27052: 5021 72353 548506 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.8* Объём цилиндра, конуса, шара
Классификатор стереометрии: Объём цилиндра, конуса, шара
Спрятать решение
·
Прототип задания
·
Видеокурс
·
Помощь
Задание 8. Математика ЕГЭ. Найти объем меньшего конуса, основание которого сечение проведенное параллельно основанию большого конуса
Задание. Объем конуса равен 152. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение:
Объем большого конуса равен:
Vб = 1/3·π·R^2·H
Vм = 1/3·π·r^2·h (1)
Так как сечение проходит через середину высоты, то H = 2h, R = 2r.
Vб = 1/3·π·(2r)^2·2h
Vб = 1/3·8·π·r^2·h (2)
Найдем отношение (1) ко (2) формуле:
Vм/Vб = 1/8
Vм = 1/8·Vб
Vм = 1/8·152 = 19.
Ответ: 19.
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование
Геннадий Викторович
Знаток
(275),
закрыт
10 лет назад
Объем конуса равен 40. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Timmy White
Профи
(551)
11 лет назад
Меньший конус подобен большому с коэффициентом подобия 1/2.(Так как отношение радиусов их оснований 1/2) Поэтому объемы относятся как (1/2)*(1/2)*(1/2)=1/8. объём меньшего равен 40/8=5.
Точнее, они подобны с коэф. 1/2 так как их высоты относятся как 1/2.
Татьяна Голубенко
Гуру
(4073)
11 лет назад
Объем большего конуса V = 1/3 * П*R^2 * H
Объем меньшего конуса v = 1/3 * П *r ^2 * h
h = 1/2H
r = 1/2 R
v = 1/3 * П (1/2R)^2 * 1/2 H = 1/3 * П *R^2 * H * 1/8 = 1/8 V = 1/8 * 40 = 5
Объем меньшего конуса = 5.
Задание
Объем конуса равен 24. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
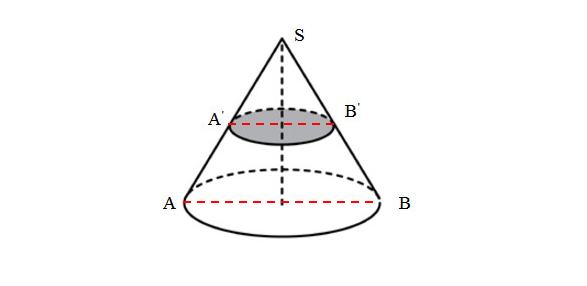
Решение
- Объем конуса равен 1/3 произведения его высоты на площадь основания, а площадь основания — это площадь круга: V=1/3*h*Socн=1/3*h*π*(D/2)2.
- Нам известно, что высота большего конуса в два раза больше высоты меньшего. Определим во сколько раз основание меньшего конуса меньше большего. Для удобства введем буквенные обозначения, как показано на рисунке, и рассмотрим треугольники АSВ и А‘SВ‘. Данные треугольники подобны. Из этого делаем вывод, что основание АВ больше основания А‘В‘ в два раза, так высота треугольника АSВ в два раза больше высоты треугольника А‘SВ‘.
- АВ и А‘В‘ являются диаметрами оснований конусов. Запишем, чему равен объем большего конуса в буквенном виде:
Vбол = 1/3*h*π*(D/2)2
- Теперь запишем, чему равен объем меньшего конуса и преобразуем получившееся выражение:
Vмен = 1/3*h/2*π*(D/2/2)2 = (1/3*h*π*(D/2)2)/(2*4) = Vбол/8 = 24/8 = 3 – объем меньшего конуса.
Ответ: 3
Задание 14752
Объем конуса равен 250. Через точку, делящую высоту конуса в отношении 3 : 2, считая от вершины, параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ: 54
Скрыть
Объём большого конуса $$V_1=picdot R^2cdot frac{H}{3},$$ где R и H – радиус основания и высота конуса, объём малого конуса $$V_2=picdot r^2cdotfrac{h}{3},$$ где r и h – радиус основания и высота конуса.
По условию, $$frac{h}{H-h}=frac{3}{2},$$ откуда $$h=frac{3}{5}cdot H.$$
Так как образующие обоих конусов лежат на одной прямой, то $$frac{H}{R}=frac{h}{r}=tgalpha,$$ где $$alpha$$ – угол наклона образующей конуса к плоскости основания.
Отсюда $$r=hcdotfrac{R}{H}=Rcdotfrac{3}{5}.$$
Тогда $$V_2=picdot(frac{3}{5})^2cdot R^2cdotfrac{3}{5}cdotfrac{H}{3}=frac{27}{125}cdotpicdot R^2cdotfrac{H}{3}=frac{27}{125}V_1=frac{27}{125}cdot250=54$$
