1. Все неравенства приводятся к “каноническому” виду, т. е Y слева, а остальное справа.
Получаются уравнения полуплоскостей. Исключением в данном задании является |y|=y. Тут надо просто сообразить. Это выражение определяет область, где переменная и её модуль имеют одинаковые знаки. Это y>=0.
2. Строятся прямые, по уравнениям “y строго равно правой части”.
Например x+y>=0; y>=-x; Уравнение: y=-x.
Если неравенство строгое, то прямая рисуется штриховой линией. В дальнейшем это означает, что точки, лежащие на прямой, не принадлежат решению. Но, как правило, если речь идёт о площадях, неравенства строгими не бывают.
3. Заштриховываются полуплоскости. Если в неравенстве знак “меньше” или “меньше или равно”, то ниже соотв. прямой, если “>” или “>=” – выше.
4. Область, в которой пересекаются ВСЕ заштрихованные области, и является той фигурой, площадь которой нужно найти.
Если координаты точек, в которых пересекаются прямые (п. 2), не очевидны, нужно будет еще решить уравнения, для нахождения точных координат. Просто приравниваются правые части и решается линейное уравнение.
Далее ищется площадь фигуры. Общего способа нет, потому как фигуры бывают разные.
Вот, собственно, и всё.
Решение этого конкретного задания не привожу.
Надеюсь, Вы сможете решить его по моему описанию.
Дана система неравенств:
Найдите площадь фигуры, координаты точек которой удовлетворяют:
а) первому неравенству системы;
б) первым двум неравенствам системы;
в) всем трем неравенствам системы.
Решение:
а) Первому неравенству, равносильному совокупности двух неравенств (х – 2)2 + у2 ≤ 4 и (х + 2)2 + у2 ≤ 4, удовлетворяют координаты точек, находящихся внутри и на границах двух кругов радиуса 2 с центрами (-2; 0), и (2; 0) (рисунок ниже). Площадь S1 этой фигуры Ф1 равна S1 = 2•Π•22 = 8Π.
б) Второму неравенству удовлетворяют координаты точек, расположенных вне квадрата с вершинами (-2; 0), (0; 2), (2; 0), (0; -2) и на его границе (рисунок ниже). Площадь S2 фигуры Ф2, координаты точек которой удовлетворяют первым двум неравенствам системы, равна S1 – S0, где S0 – половина площади круга радиуса 2, то есть S2 = 8Π — 2Π = 6Π.
в) Третье неравенство можно записать в виде (х – 4)2 – у2 ≥0 или (х + у – 4) (x – y – 4) ≥ 0. Этому неравенству удовлетворяют координаты точек, лежащих внутри и на границе одной из двух пар вертикальных углов, образующихся при пересечении прямых х + у – 4 = 0 и х – у – 4 = 0. Так как (0; 0) – решение третьего неравенства системы, то этому неравенству удовлетворяют координаты точек фигуры Ф2, лежащих в прямом угле с вершиной (4; 0) абсциссы которых х ≤ 4, ив вертикальном с ним угле.
Фигура Ф3, координаты точек которой удовлетворяют всем неравенствам системы, выделена темным фоном на рисунке выше.
Ее площадь S3 равна сумме площади круга радиуса 2 и площади прямоугольного треугольника с вершинами (2; 2), (2; -2) и (4; 0), то есть S3 = 4Π + 4.
Ответ: а) 8Π; б) 6Π; в) 4Π + 4.
Другие задачи на координатную плоскость читайте здесь.
Уравнением линии на плоскости называют уравнение с двумя переменными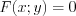 
или 
, которому удовлетворяют координаты 
(абсцисса) и 
(ордината) любой точки данной линии.
Уравнение окружности
Рассмотрим расположение окружности на координатной плоскости:
1) если уравнение окружности имеет вид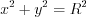 
, то ее центр находится в точке 
, а радиус равен 
(рис. 2.51);
2) если уравнение окружности имеет вид 
, то ее центр находится в точке 
, а радиус равен (рис. 2.52).
Заметим, что неравенству 
удовлетворяют координаты всех точек плоскости, лежащих внутри окружности 
, а неравенству 
удовлетворяют координаты всех точек, лежащих вне этой окружности. Неравенству 
удовлетворяют координаты всех точек плоскости, лежащих внутри окружности и на ее границе.
Уравнение квадрата
Рассмотрим расположение квадрата на координатной плоскости:
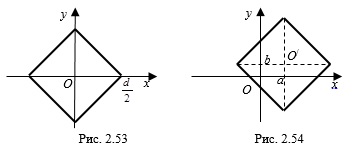
1) если уравнение квадрата имеет вид 
, то точка – точка пересечения диагоналей квадрата, 
– длина диагонали квадрата (рис. 2.53);
2) если уравнение квадрата имеет вид 
, то точка – точка пересечения диагоналей квадрата, – длина диагонали квадрата (рис. 2.54).
Пересечение линий на плоскости
Рассмотрим две линии, заданные уравнениями 
и 
. Чтобы найти точку пересечения этих линий необходимо решить систему уравнений 
Графическое решение уравнений и неравенств
1. Рассмотрим уравнение 
. Это уравнение можно решить графически, если построить в одной системе координат графики функций , 
и найти их точки пересечения. Абсциссы точек пересечения и будут корнями уравнения .
2. Использование монотонности функций при решении уравнений: если функция 
строго возрастает, а функция 
строго убывает на некотором множестве, то графики этих функций имеют не более одной точки пересечения, а уравнение на этом множестве имеет не более одного решения. Поэтому, чтобы решить такие уравнения можно подобрать (если это удается) число, которое является их корнем. На рисунке 2.55 число 
– корень уравнения . Аналогично решаются уравнения, если функция имеет вид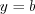 
(эта прямая параллельна оси абсцисс) (рис. 2.56).
Например, число 
является единственным корнем уравнения 
, так как левая часть этого уравнения представлена строго убывающей функцией, а правая – строго возрастающей.
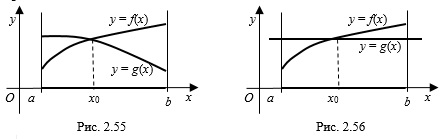
3. Использование монотонности функций при решении неравенств: если функция строго возрастает на некотором отрезке ![LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png "[a;b]")
, а функция строго убывает на этом отрезке и – корень уравнения , то решением неравенства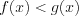 
является промежуток 
, а решением неравенства 
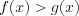является промежуток ![LaTeX formula: (x_{0};b]](https://helpy.quali.me/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png "(x_{0};b]")
(рис. 2.57).
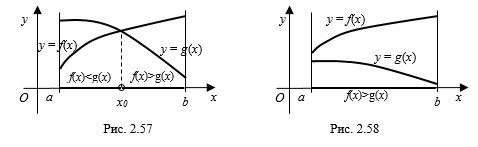
Графики функций на заданном отрезке могут и не пересекаться. Например, на рисунке 2.58 неравенство 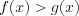выполняется на всем отрезке .
Пример 1. Найдите площадь фигуры, ограниченной прямыми 
, 
и 
.
Решение. Построим на координатной плоскости данные прямые (рис. 2.59).
Прямая (1) параллельна оси ординат и проходит через точку 
. Чтобы построить прямую (2), необходимо знать две точки, принадлежащие этой прямой. Например, можно построить точки 
, 
и провести через них прямую (2). Чтобы построить прямую (3), можно построить точки 
и 
, принадлежащие этой прямой, и провести через них прямую (3).
Из рисунка 2.59 видим, что треугольник 
ограничен данными прямыми. Площадь полученного треугольника найдем по формуле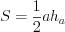 
, а в нашем случае 
.
Найдем координаты точек пересечения прямых.
1. Найдем координаты точки 
, решая систему уравнений 
Получим точку 
.
2. Найдем координаты точки 
, решая систему уравнений 
Получим точку 
.
3. Найдем координаты точки 
, решая систему уравнений 
Получим точку 
.
Найдем длину отрезка 
, вычитая из ординаты точки ординату точки . Получим 
. Найдем длину отрезка 
, вычитая из абсциссы точки абсциссу точки : 
. Найдем площадь треугольника : 
.
Ответ: 
.
Пример 2. Найдите площадь фигуры, заданной на координатной плоскости системой неравенств 
Решение. Построим гранич-ные прямые, соответствующие неравенствам заданной системы: 
(1), 
(2), 
(3), 
(4) (рис. 2.60). Система неравенств задает на координатной плоскости трапецию 
, площадь которой найдем по формуле 
.
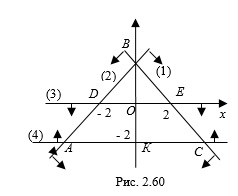
Согласно рисунку 2.60 запишем: 
, 
.
Найдем координаты точки , решая систему уравнений 
Получим 
. Аналогично найдем координаты точки . Получим 
. Тогда 
.
Найдем площадь трапеции: 
.
Ответ: 
.
Пример 3. Найдите все целые значений параметра 
, при которых уравнение 
имеет шесть корней.
Решение. Заменим данное уравнение равносильной системой уравнений 
Построим схематически график функции 
, предварительно построив графики функций 
и 
.
1. Графиком функции является парабола, ветви которой направлены вверх. Найдем координаты вершины параболы.
Согласно формулам 
, 
получим: 
, 
. Найдем нули функции (точки пересечения графика с осью абсцисс), решая уравнение 
. Получим 
, 
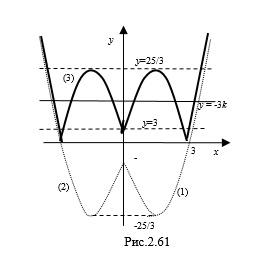
. Найдем точку пересечения графика с осью ординат: 
. Построим график (1) (рис. 2.61).
2. Рассмотрим функцию 
. Поскольку 
, то запишем 
. Построим график (2) этой функции, выполняя следующее преобразование: часть графика функции 
правее оси 
оставим и ее же отразим симметрично этой оси (рис. 2.61).
3. Построим график (3) функции 
, выполняя следующее преобразование: часть графика функции , расположенной над осью 
оставим, а ту, что под осью , отразим симметрично этой оси (рис. 2.61).
Рассмотрим линейную функцию 
. Построим семейство прямых, параллельных оси так, чтобы они пересекали график функции в шести точках. Это возможно при условии, что 
или 
. Очевидно, что промежутку 
принадлежит одно целое значение 
.
Ответ: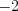 
.
Пример 4. Найдите все значения параметра 
, при которых уравнение 
имеет один корень.
Решение. Решим уравнение графически, заменив его равносильной системой уравнений 
1. Построим схематически график функции 
(рис. 2.62). Для этого найдем нули функции под знаком модуля: 
, 
и раскроем модуль на полученных промежутках, учитывая при этом, что – точка разрыва функции.
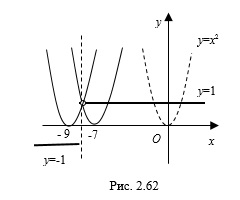
Рассмотрим два случая:
1) если 
, то 
или 
;
2) если 
, то 
или 
.
2. Построим схематически график функции 
, предварительно построив параболу 
.
Парабола и прямая имеют две общие точки. Так как согласно условию задачи графики функций и должны иметь только одну точку пересечения, то, выполняя параллельный перенос параболы 
на единичных отрезка влево, заметим, что при 
парабола и прямая имеют одну точку пересечения, а при 
уже не имеют общих точек. Следовательно, если принимает значения из промежутка 
, то графики функций и имеют одну общую точку, а уравнение имеет одно решение.
Ответ: .
Построим прямую 
так, чтобы она имела с графиком функции 
бесконечно много общих точек. Очевидно, что это возможно в том случае, если 
, откуда ![LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png "a=-2sqrt[3]{2}")
.
Ответ: .
Пример 6. Найдите все значения параметра , при которых система уравнений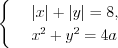 
имеет четыре решения.
Решение. Имеем уравнение квадрата 
и уравнение окружности 
.
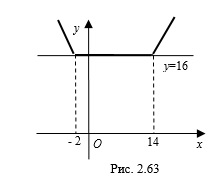
1. Построим квадрат с центром в точке и диагональю 
(рис. 2.64).
Площадь квадрата найдем по формуле 
. Получим: 
. С другой стороны площадь квадрата можно вычислить по формуле 
, где – сторона квадрата. Тогда 
и 
.
2. Построим окружность с центром в точке и радиусом 
(рис. 2.64). Поскольку система уравнений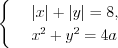 
имеет четыре решения, то окружность должна быть вписана в квадрат, тогда ее радиус 
или 
, откуда 
или описана около квадрата, тогда радиус окружности 
или 
, откуда 
.
Ответ: 
; 
.
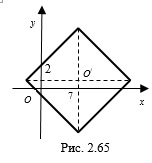
Пример 7. Найдите площадь и периметр фигуры, заданной неравенством 
.
Решение. Данному неравенству удовлетворяют координаты всех точек плоскости, расположенных внутри квадрата 
и на его границе.
Построим квадрат с центром в точке 
и диагональю 
(рис. 2.65). Найдем площадь квадрата. Согласно формуле получим 
.
С другой стороны площадь квадрата находят по формуле 
, где – сторона квадрата.
Тогда 
, 
. Найдем периметр квадрата: 
.
Ответ: 
, 
.
Решая уравнение или систему уравнений графически, точное решение найти бывает достаточно сложно, а то и вовсе не возможно. Поэтому этот метод чаще всего применяют в случае, когда необходимо определить количество корней уравнения или найти их приближенное значение.
Найдите площадь фигуры, заданной системой неравенств ответ есть:7.5
Светило науки – 28486 ответов – 90605 раз оказано помощи
(1)y≥0,5x
x -2 0
y -1 0
Строим прямую у=0,5х
Решение -полуплоскость выше прямой
(2)у≥-2х
х -2 0
у 4 0
Строим прямую у=-2х
Решение -полуплоскость правее прямой
(3)у≤3-х
х 0 2
у 3 1
Строим прямую у=3-х
Решение -полуплоскость левее прямой
Фигура полученная при пересечении полуплоскостей -треугольник
(1) и (2) прямые пересекаются в точке А(0;0)
(2) и (3) прямые пересекаются в точке В(-3;6)
(1) и (3) прямые пересекаются в точке С(2;1)
Найдем стороны треугольника
АВ²=(0+3)²+(0-6)²=9+36=45 АВ=√45
ВС²=(2-0)² +(1-0)²=4+1=5 ВС=√5
АС²=(2+3)²+(1-6)²=25+25=50 АС=√50
АС²=АВ²+ВС²⇒треугольник прямоугольный⇒
S=1/2*AC*BC=1/2*√45*√5=1/2√225=1/2*15=7,5
Найдите площадь фигуры, заданной системой неравенств Можно просто ответ.
Вы зашли на страницу вопроса Найдите площадь фигуры, заданной системой неравенств Можно просто ответ?, который относится к
категории Алгебра. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 – 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
