Как найдите площадь кольца ограниченного концентрическими окружностями

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

1 мая

Новый сервис: можно исправить ошибки!

1 мая

Бесплатные курсы подготовки к ЕГЭ и ОГЭ

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Задания

Версия для печати и копирования в MS Word

Задания Д5 № 27642

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и

Спрятать решение

Решение.

Площадь круга определяется формулой S = πR². Площадь кольца равна разности площадей первого и второго круга. Тогда

Поэтому площадь кольца: S  =  S₁ − S₂  =  16 − 4  =  12.

Ответ: 12.

Аналоги к заданию № 27642: 57507 57509 509456 … Все

Спрятать решение

Помощь

О проекте · Редакция · Правовая информация · О рекламе

Источник

Площадь кольца

Онлайн калькулятор

Площадь кольца по радиусам или диаметрам

Чему равна площадь кольца ограниченного двумя окружностями, если:

у внешней окружности
у внутренней окружности

Площадь кольца по толщине и любому другому параметру

Чему равна площадь кольца ограниченного двумя окружностями, если:

толщина кольца t =

Теория

Площадь кольца через радиусы

Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?

Формула

Пример

К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:

S = 3.14 ⋅ (3² – 2²) = 3.14 ⋅ (9 – 4) = 3.14 ⋅ 5 = 15.7 см²

Ответ: S = 15.7 см²

Площадь кольца через диаметры

Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?

Формула

Пример

К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:

S = 3.14 / 4 ⋅ (4² – 2²) = 0.785 ⋅ (16 – 4) = 9.42 см²

Ответ: S = 9.42 см²

Площадь кольца через толщину

Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:

внешний диаметр D
внутренний диаметр d
радиус внешней окружности R
радиус внутренней окружности r

Формулы

Пример

Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:

S = 3.14/4 ⋅ (5² – (5 – 2 ⋅ 2)²) = 0.785 ⋅ (25 – 1) = 18.84 см²

№ 54. Найдите площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 ми 6,5 м; 3) а и b, а > b.

Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №54
к главе «§14. Площади фигур».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b?

Геометрия | 5 – 9 классы

Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b.

Первая окружность с радиусом R₁

Длина окружности L = 2πR

b = 2πR₁⇒ R₁ = b / 2π

а = 2πR₂ ⇒ R₂ = а / 2π

Площадь окружности S = πR²

площадь кольца равна S₁ – S₂ = π(R₁² – R₂²) = π((b / 2π ) ² – (а / 2π)²) = (b² – а²) / 4π.

Найти площадь кругового сектра(кольца) заключенного между двумя окружностями, с одним и тем же центром и радиусом 4 и 6 см?

Найти площадь кругового сектра(кольца) заключенного между двумя окружностями, с одним и тем же центром и радиусом 4 и 6 см.

(подробно и с объяснением).

Площадь кругового кольца, находящегося между двумя окружностями с общим центром, равна 12дм², радиус одной окружности в 2 раза больше, чем радиус другой?

Площадь кругового кольца, находящегося между двумя окружностями с общим центром, равна 12дм², радиус одной окружности в 2 раза больше, чем радиус другой.

Найдите эти радиусы.

Даны две концентрические окружности, длина одной из них 33п см, а другой 27п см?

Даны две концентрические окружности, длина одной из них 33п см, а другой 27п см.

Найдите ширину кольца.

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности?

В кольце, образуемом двумя концентрическими окружностями, проведена хорда, касающаяся меньщей окружности.

Найдите площадь кольца , если известно, что длина хорды равна 8 см.

Около правильного треугольника описана окружность и в него вписана окружность?

Около правильного треугольника описана окружность и в него вписана окружность.

Длина меньшей окружности равна 8пи.

Найдите площадь кольца и площадь треугольника.

Срочно?

№8. Радиусы двух концентрических окружностей относятся как 4 : 5.

Найдите их диаметры, если ширина кольца, образованного этими окружностями, равна 7 см.

№9. Найдите радиусы двух концентрических окружностей, если известно, что их диаметры относятся как 2 : 5 и ширина кольца, образованного этими окружностями, равна 24 см.

Помогите плииииииииииииииз?

От этой оценки зависит четвертная!

1. Фигура, ограниченная двумя концентрическими окружностями, называется кольцом, а разность радиусов данных окружностей – шириной этого кольца.

1) выразите ширину кольца через длины окружностей

2) радиусы окружностей равны 26см и 10см.

Найдите длину наибольшего отрезка, который целиком можно поместить в данное кольцо

Какую часть площади круга составляет площадь сектора, центральный угол которого равен 1)30°, 2)45°, 3)60°, 4)90°, 5)180°, 6)300°.

Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2?

Площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром, равна 8 см2.

Найдите площади этих кругов, ограниченными этими окружностями, если радиус одной из них в три раза больше, чем радиус другой.

В правильный треугольник со стороной 4 см вписана окружность и около него описана окружность?

В правильный треугольник со стороной 4 см вписана окружность и около него описана окружность.

Найдите площадь кольца, заключенного между этими окружностями.

Ширина кольца, образованного концентрическими окружностями радиусов 3 см и 5 см, равна ?

Ширина кольца, образованного концентрическими окружностями радиусов 3 см и 5 см, равна :

На этой странице сайта размещен вопрос Найдите площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны а и b, где а < ; b? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 – 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

МК||АС, АВ – секущая. По свойству углов, образованных при пересечении параллельных прямых секущей соответственные ∠ВМК = ∠ВАС = 80° MN – биссектриса, ∠ВМN = ∠KMN = 80° : 2 = 40° ВС – секущая при параллельных МК и АС. ⇒соответственные ∠ВКМ = ∠ВСА = ..

Ты знаешь чему равна длина отрезка ВС , и знаешь длина АС, и тут ты можешь так. BC – AC = BA 8 – 3 = 5.

З вeршини кута провeдeно промінь , пeрпeндикулярний до його бісeктриси , який утворює зі стороною даного кута гострий кут, градусна міра якого в 4 рази більша за даний кут . Знайдіть даний кут.

Площадь треугольника S = (a²·sinα) / 2, где а – боковая сторона, α – угол при вершине. A² = 2S / sinα = 2·48 / 0. 5 = 192, a = 8√3 см – это ответ.

Периметр прямоугольника рассчитывается по формуле : P = 2(a + b) Подставим значения a и b в формулу и получим : P = 2(10 + 8) = 36 см Ответ : 36 см.

Три прямые пересекаются в одной точке и образуют шесть углов. Найдите сумму трёх из этих углов, которые попарно не имеют общих точек.

Известно : биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам (в нашем случае – катетам), т. Е. дано отношение катетов 15 : 20 = 3 : 4 отношение катетов – – это тангенс острого угла в прямоугольном треугольнике и..

[spoiler title=”источники:”]

http://5terka.com/node/737

http://geometria.my-dict.ru/q/1739191_najdite-plosad-krugovogo-kolca-zaklucennogo-mezdu/

[/spoiler]

Источник

{S = pi (R^2 – r^2)}

С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.

Содержание:

калькулятор площади кольца
формула площади кольца через радиусы
формула площади кольца через диаметры
примеры задач

Формула площади кольца через радиусы

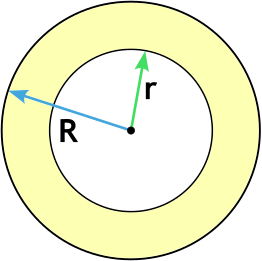
{S = pi (R^2 – r^2)}

R – внешний радиус кольца

r – внутренний радиус кольца

Формула площади кольца через диаметры

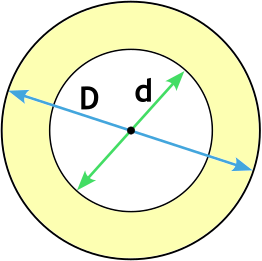
{S= dfrac{pi}{4}(D^2 – d^2)}

D – внешний диаметр кольца

d – внутренний диаметр кольца

Примеры задач на нахождение площади кольца

Задача 1

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.

Решение

В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.

S = pi (R^2 – r^2) = pi (7^2 – 3^2) = pi (49 – 9) = 40pi approx 125.66371 : см^2

Ответ: 108 cdot 0.866 approx 93.53074 : см^2

Полученный ответ можно проверить с помощью калькулятора .

Задача 2

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны dfrac{4}{sqrt{pi}} и dfrac{2}{sqrt{pi}}.

Решение

Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.

S = pi (R^2 – r^2) = pi ({Big(dfrac{4}{sqrt{pi}} Big) }^2 – {Big(dfrac{2}{sqrt{pi}} Big) }^2) = pi (dfrac{16}{pi} – dfrac{4}{pi}) = pi dfrac{12}{pi} = 12 : см^2

Ответ: 12 : см^2

Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:

dfrac{4}{sqrt{pi}} : rarr : 4/sqrt(pi)

dfrac{2}{sqrt{pi}} : rarr : 2/sqrt(pi)

Если ввести данные в таком формате, можно проверить ответ .

Задача 3

Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.

Решение

Задача аналогична предыдущим.

S = pi (R^2 – r^2) = pi (15^2 – 13^2) = pi (225 – 169) = 56pi approx 175.92919 : см^2

Ответ: 56pi approx 175.92919 : см^2

Проверка .

Задача 4

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

Решение

Задача аналогична предыдущим.

S = pi (R^2 – r^2) = pi (13^2 – 12^2) = pi (169 – 144) = 25pi approx 78.53982 : см^2

Ответ: 25pi approx 78.53982 : см^2

Проверка .

Источник

Площадь кольца

Главная
/
Математика
/
Геометрия
/
Площадь кольца

Чтобы найти площадь кольца, ограниченного двумя концентрическими окружностями, воспользуйтесь нашим очень удобным онлайн калькулятором: